Assignment on Mathematical Methods and Statistical Techniques

Mathematical Methods and Statistical Techniques
M/615/1476
1/1/2020
[Type the company name]

Contents
Part 1:..........................................................................................................................................................3
Problem (a)..............................................................................................................................................3
Problem (b)..............................................................................................................................................4
Problem (c)..............................................................................................................................................5
Problem (d)..............................................................................................................................................6
Problem (e)..............................................................................................................................................7
Problem (f)...............................................................................................................................................8
Problem (g)............................................................................................................................................10
Problem (h)............................................................................................................................................11
Problem (i).............................................................................................................................................13
Part 2:........................................................................................................................................................15
Problem (a)............................................................................................................................................15
Problem (b)............................................................................................................................................16
Problem (c)............................................................................................................................................18
Problem (d)............................................................................................................................................20
Conclusion.................................................................................................................................................21
References.................................................................................................................................................22
2 | P a g e

Part 1:
Problem (a)
Solution:
The Dimensions of Power, P = ML^2T^-3
And the Dimension of Voltage, V = L^0.5 M^0.5 T^-1
3 | P a g e

Since the equation of power dissipation across the Resistor is given by
So, Resistance, R is given by
So, the Dimensions of R is
(L^0.5 M^0.5 T^-1)^2/ ML^2T^-3
= L^-1T^2
Problem (b)
Solution:
The LHS of the equation is time period of Vibration of string
t with Dimension [T]
the right hand side of the equation will have the dimension
2π = no dimension
m^3 = [M^3]
4 | P a g e

l= [L^1]
F = [MLT^−2]
So, as per equation RHS has dimensioned,
([M^3] [L^1]/ [MLT^−2])^0.5
=([M^2T^2])^0.5
So, RHS dimension = [MT]
So, LHS dimension is not equal to the dimension of RHS, so the equation is not correct.
Problem (c)
Solution:
The samples are given in the question are 2, 4, 6, 8, 10…40, in mV unit
So these are in Arithmetic progression with
First value, a= 2
Difference between consecutive numbers, d= 2 and
Number of values, n = 20
So, sum of these 20 voltage samples will be
S= n/2[2a+ (n-1) d]
S= 20/2[2*2+ (20-1)*2] =420 mV
So, the sum of these 20 voltage samples is 420 mV.
5 | P a g e

Problem (d)
6 | P a g e

Solution: (Minlos, 2000)
The digital chip is counting the sequence in Geometric Progression.
The nth value in G.P is given by
Tn= arn-1
Where, a= first value
r= common ration
n= number of terms
In the question
First value, a = 1024
Common ratio, r = 2
Number of terms, n = 9
So, 9th count of the chip is
T9= 1024*29-1 =1024*28 = 262144
So, the 9th count of the chip is 262144.
Problem (e)
Solution:
7 | P a g e

As per the question a electrical circuit having capacitor and resistor connected in series with DC supply is
having following parameters
Resistor, R = 1MΩ
Vs= 12 V
Vc= 2 V, when time, t=4 sec
So, from the equation to find the voltage across the capacitor
2=12(1-e-4/RC)
So, 1-e-4/RC=1/6
e-4/RC=1-1/6
-4/RC=ln(0.833)
RC=21.89
So, C = 21.89/106 = 21.89 μF
Problem (f)
Solution:
8 | P a g e

The signal used in the question is described by the formula
Where,
Vs is the instantaneous voltage
Amplitude = 6
Frequency, f=1MHz =10^6 Hz
Phase = -π/4
The instantaneous voltage is given as Vs=3 V
So using the equation
3=6sin(2 πft- π/4)
2 πft- π/4=sin-1(0.5)
Time , t= (sin-1(0.5)+ π/4)/ 2 πf
T=2.083333333 ×10^-7 =0.2 μsec
The test signal is simulated in MATLAB software and the figure is shown blow :
9 | P a g e

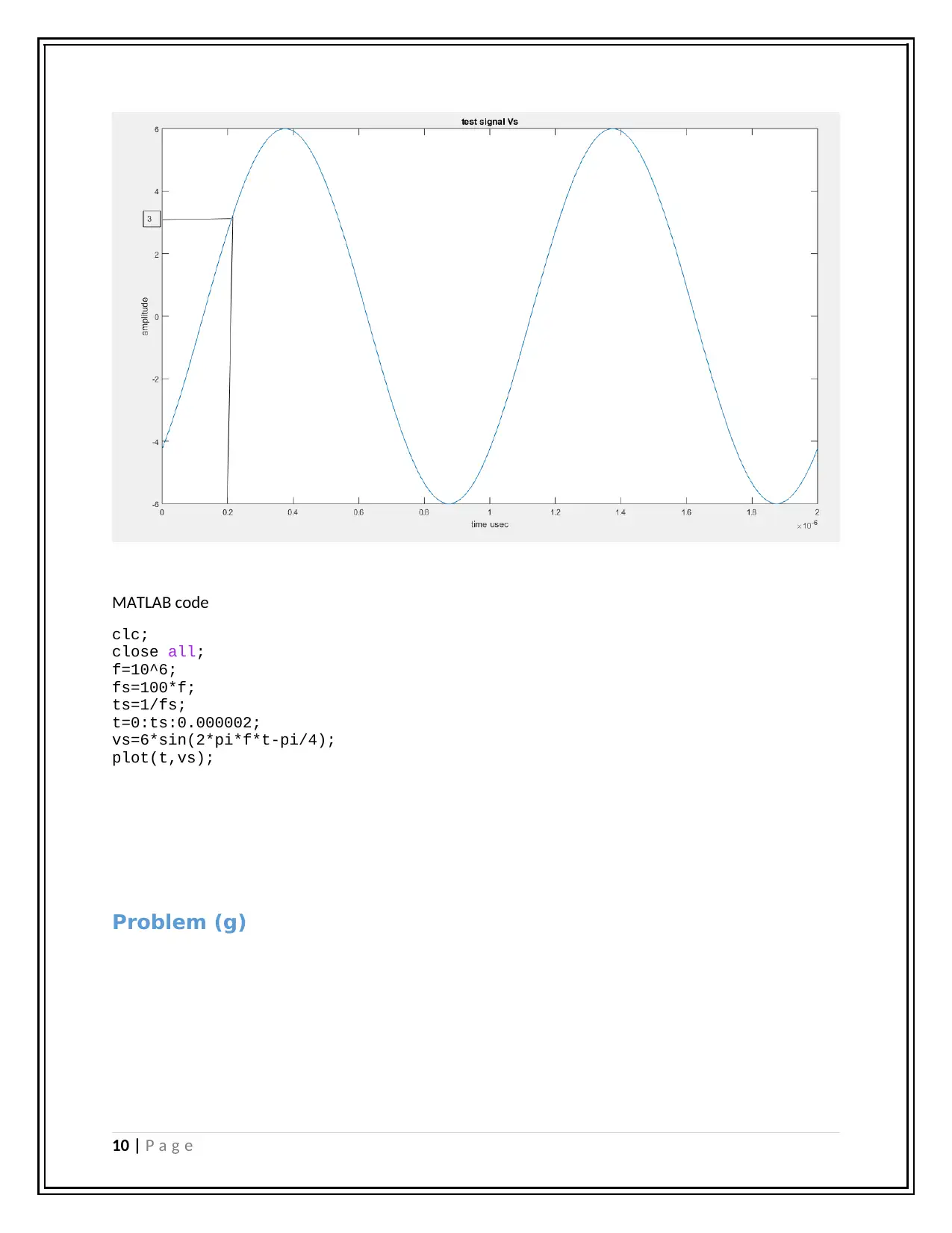
MATLAB code
clc;
close all;
f=10^6;
fs=100*f;
ts=1/fs;
t=0:ts:0.000002;
vs=6*sin(2*pi*f*t-pi/4);
plot(t,vs);
Problem (g)
10 | P a g e

Solution: (Thompson, 2016)
In this question the described equation for heavy power cable is given as
i) The value of y when x is 104
Y=60cosh(104/60)
Y=60.02745827748
ii) The value of x when y is 180
X=60*cosh-1(180/60)
X=6059.87840526312
Problem (h)
11 | P a g e

Solution: (Thompson, 2016)
The period (t) of the pendulum swing depends on
Mass attached =m
Length of the string =l
Acceleration due to gravity =g
Dimension of acceleration due to gravity, g = [LT^-2]
Dimension of l =[L]
Dimension of m=[M]
Let , time period
T ∝ la
T ∝ mb
T ∝ gc
Combining the above equation
T ∝ lambgc
T =K.lambgc
Where, k = constant
Writing above equation in dimensions
[T]= [L] ^a [M] ^b [LT^-2]^c
[M0L0T1]= [Mb][La][LcT-2c]
[M0L0T1]= [MbLa+cT-2c]
Equating the powers of M,L and T
12 | P a g e

b=0 ………………… (1)
a+c=0 ………………… (2)
-2c=1 ……………….. (3)
From equation (3)
C=-1/2
From equation (2) and (3)
a=1/2
so, a=1/2,b=0,c=-1/2
so, from the equation
t=k.l1/2m0g-1/2
So, time period of pendulum is
t=k. √(l/g)
From various methods we find constant k = 2π
So,
Time period, t=2π √(l/g)
Problem (i)
Solution: (Minguez, 2008)
The speed of the sound is influenced by
Gas pressure having dimension, p= [M L−1 T−2]
Gas density, r= [ML-3]
13 | P a g e

Acceleration due to gravity, g = [LT-2]
The speed of sound, u= [LT-1]
Let the speed of sound,
u ∝ pa
u ∝ rb
u ∝ gc
So, the equation, u=k. parb gc
Writing above equation in dimensions
[LT-1]= [M L−1 T−2]^a[ML-3]^b[LT-2]^c
[LT-1]= [Ma L−a T−2a] [Mb L-3b][Lc T-2c]
[LT-1]= [Ma+b L−a-3b+c T−2a-2c]
Equating the powers of M, L, T
a+b=0 ………………(1)
-a-3b+c=1…………….. (2)
-2(a+c) =-1…………… (3)
From equation (1),(2),(3)
a=1/2
b=-1/2
c=0
So, putting values a, b, c in the equation, u=k. parb gc
U=k.p1/2r-1/2g0
14 | P a g e

U=k√(p/r)
Part 2:
Problem (a)
Solution:(Minguez, 2008)
i) The mean transmit power for the samples
Are given by the formula
Where,
= sum of values
= mean value
n= number of values
So, mean transmit power = (18.1+19.2+18.4+18.1+19.9+18.1+17.4+19.1+18.1+17.4)/10
= 18.38
15 | P a g e

ii) Standard deviation for the samples is given by the following formula
So, s= sqrt([(18.1-18.38)2+(19.2-18.38)2+(18.4-18.38)2+(18.1-18.38)2+(19.9-18.38)2+(18.1-
18.38)2+(17.4-18.38)2+(19.1-18.38)2+(18.1-18.38)2+(17.4-18.38)2]/9)
S=0.7983
iii) Tally chart to show frequency of measured transmit power
Power(+dBm) Tally Total
18.1 IIII 4
19.2 I 1
18.4 I 1
19.9 I 1
17.4 II 2
19.1 I 1
So, the frequency of measured transmit power is more for 18.1 dBm.
Problem (b)
16 | P a g e

Solution:
In this problem binomial probability distribution is used to calculate the probabilities
(Binomial distribution, 2020)
i) When two of the six bolts exceed the diameter
94% of the bolts are in allowable limits of diameter
SO, equation for the binomial distribution is:
Here, k=4,
N=6
P=0.94
So, putting the values in the equation
P (4) = 15*0.944(1-0.94)2 =0.0421
Therefore probability that two of the 6 bolts exceed the diameter is 0.0421
ii) The probability that more than two bolts exceed the diameter will be determined by adding
all the probabilities for k =3,k=2,k=1, and k=0, (Binomial distribution, 2020)
17 | P a g e

P(3)= 20*0.943(1-0.94)3=0.00358
P(2)=15*0.942(1-0.94)4=0.000172
P(1)=6*0.941(1-0.94)5=0.00000438
P(0)=1*0.940(1-0.94)6=4.66x10^-8
Summing p(3), p(2), p(1), p(0)
Probability that more than two bolts exceed the diameter =0.036
Problem (c)
Solution:
(Z Scores (Z Value) & Z Table & Z Transformations | Six Sigma Study Guide, 2020)
Number of capacitors= 400
18 | P a g e

mean capacitance = 100 uF
standard deviation= 7 uF
First we need to calculate the z score using the following formula
For x=90 uF
Z= (90-100)/7 = -1.4285
So, from the z-table
So, solution to lower bound is 0.0778 = 7.78% …………….(1)
And for x=110 uF
Z= (110-100)/7 =1.4285
From the z table
19 | P a g e

So, solution to upper bound is 100%-42.22%=57.78% …………(2)
Adding (1) and (2)
We get 65.56 %
So, percentage of capacitors in the range 90 uF to 110 uF is 100-65.56 % = 34.44 %
So, number of capacitor in this range is (34.44/100)*400 =138
Problem (d)
Solution:
(Z Scores (Z Value) & Z Table & Z Transformations | Six Sigma Study Guide, 2020)
Number of sample amount of additive =100
20 | P a g e

Without the additive mean mpg figure =44
With the additive mean mpg figure =48
Standard deviation = 13 mpg
So in this case we will use z-score
For x=50 mpg when calculating z
First without adding additive
Z=(50-44)/13=0.46
By using z score table we get the value 0.17724
So, more than 100%-17.7% =82.3 % have more mpg than 50
After adding additive
Z=(50-48)/13 = 0.15
By using z score table we get the value 0.05962
So, more than 100%-5.96% =94.04 % have more mpg than 50
By using z-score analysis we can say that the results of the testing are correct and after using additive
the mpg value of the car goes up.
Conclusion
21 | P a g e

In this assignment the problems related to Mathematical Methods and Statistical Techniques were
solved. The mathematical equations and charts are duly shown and explained in each problem. The
problems shows the understanding of real life problems of engineering and science , also experiments
and software analysis is added to better understand the problems.
References
Biskup, M. and Kotecký, R. (2009) Methods Of Contemporary Mathematical Statistical Physics, Berlin, Springer.
Minguez, R. (2008) Advances In Mathematical And Statistical Modeling, Boston, Birkhäuser Boston.
Minlos, R. (2000) Introduction To Mathematical Statistical Physics, Providence, RI, American Mathematical Society.
Thompson, C. (2016) Mathematical Statistical Mechanics, [Place of publication not identified], Princeton University
Pres.
Z Scores (Z Value) & Z Table & Z Transformations | Six Sigma Study Guide (2020) Six Sigma Study Guide, [Online].
Available at https://sixsigmastudyguide.com/z-scores-z-table-z-transformations/ (Accessed 5 January 2020).
Binomial distribution (2020) En.Wikipedia.Org, [Online]. Available at https://en.wikipedia.org/wiki/Binomial_distribution
(Accessed 5 January 2020).
22 | P a g e