MATLAB Simulink Design of a Ship Roll Stabilization System
VerifiedAdded on 2023/06/14
|20
|1517
|463
Homework Assignment
AI Summary
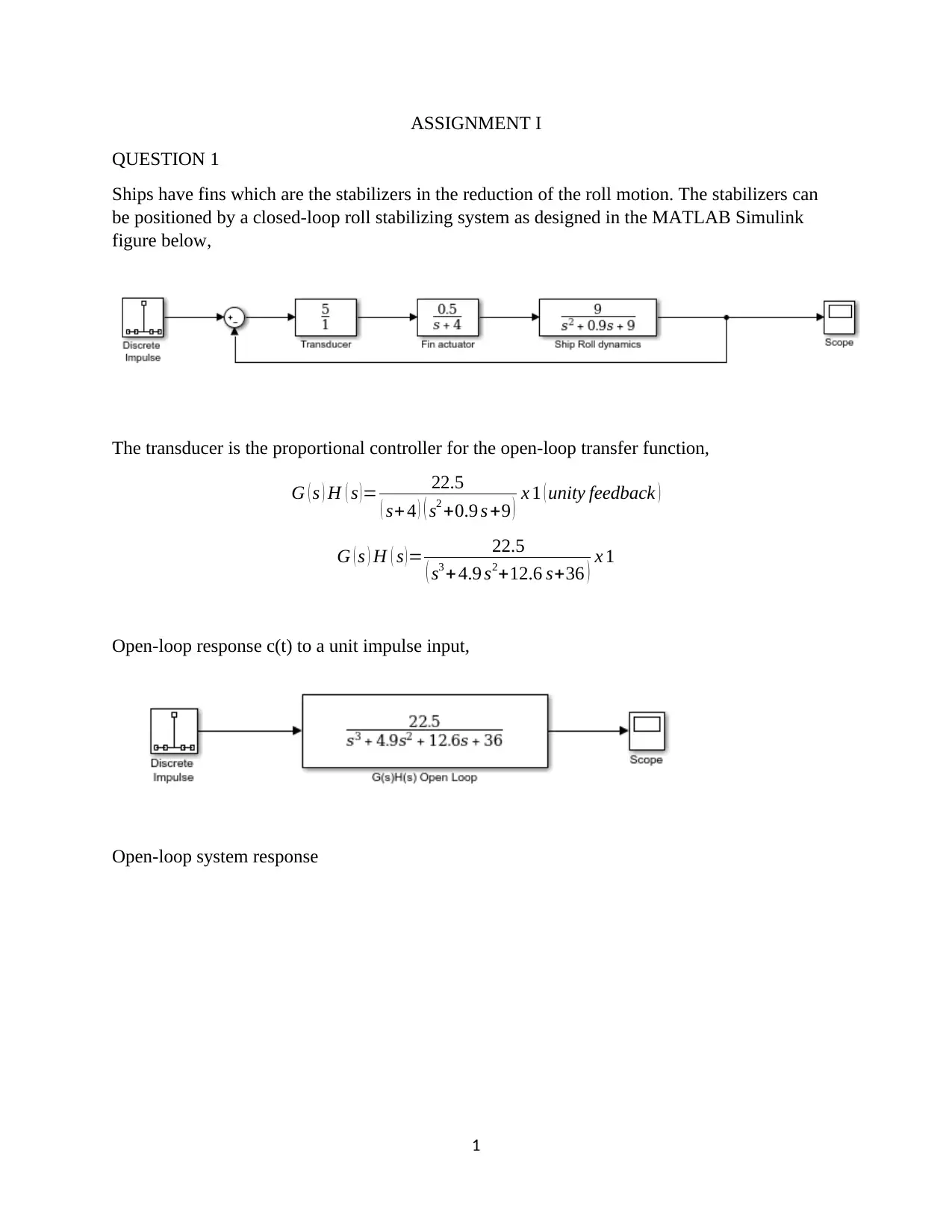
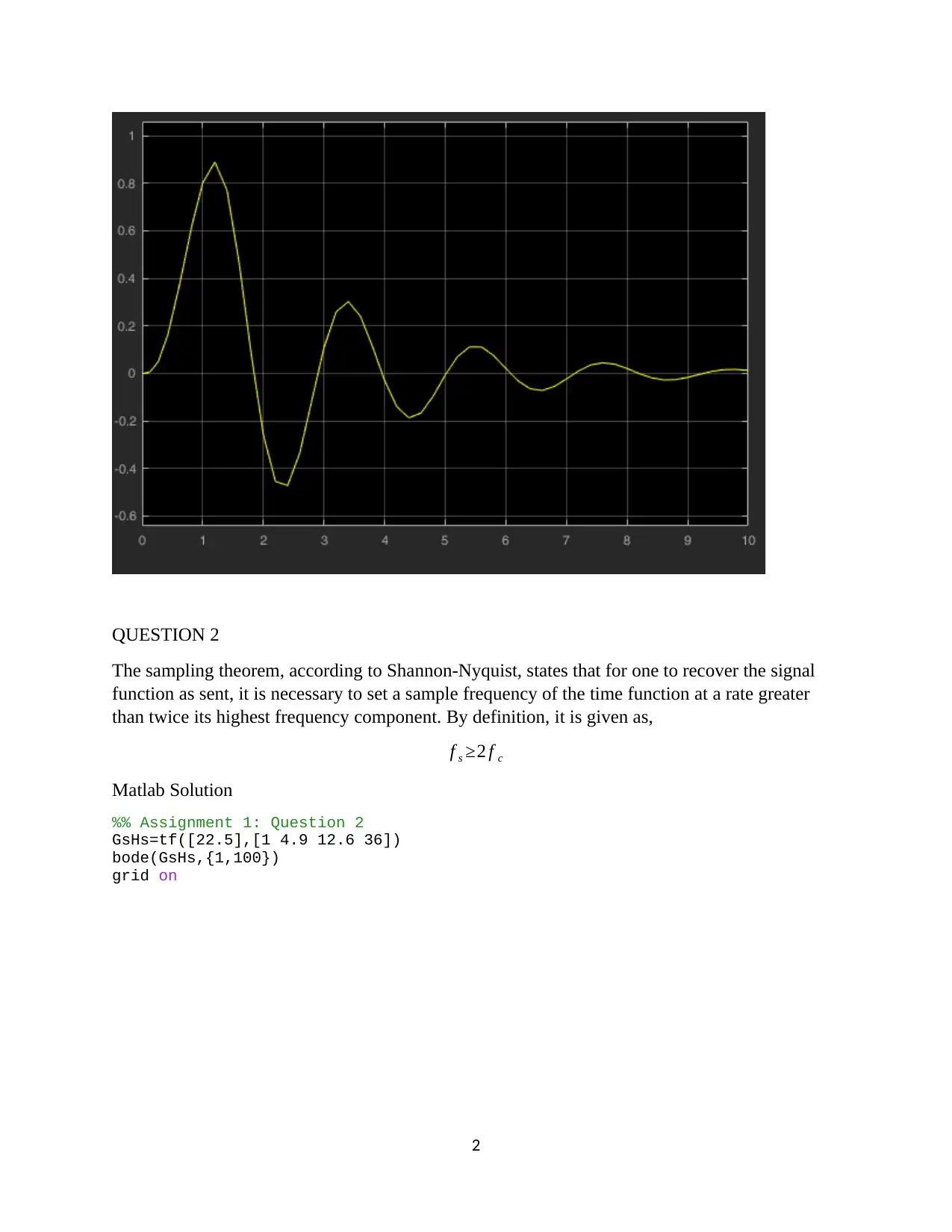
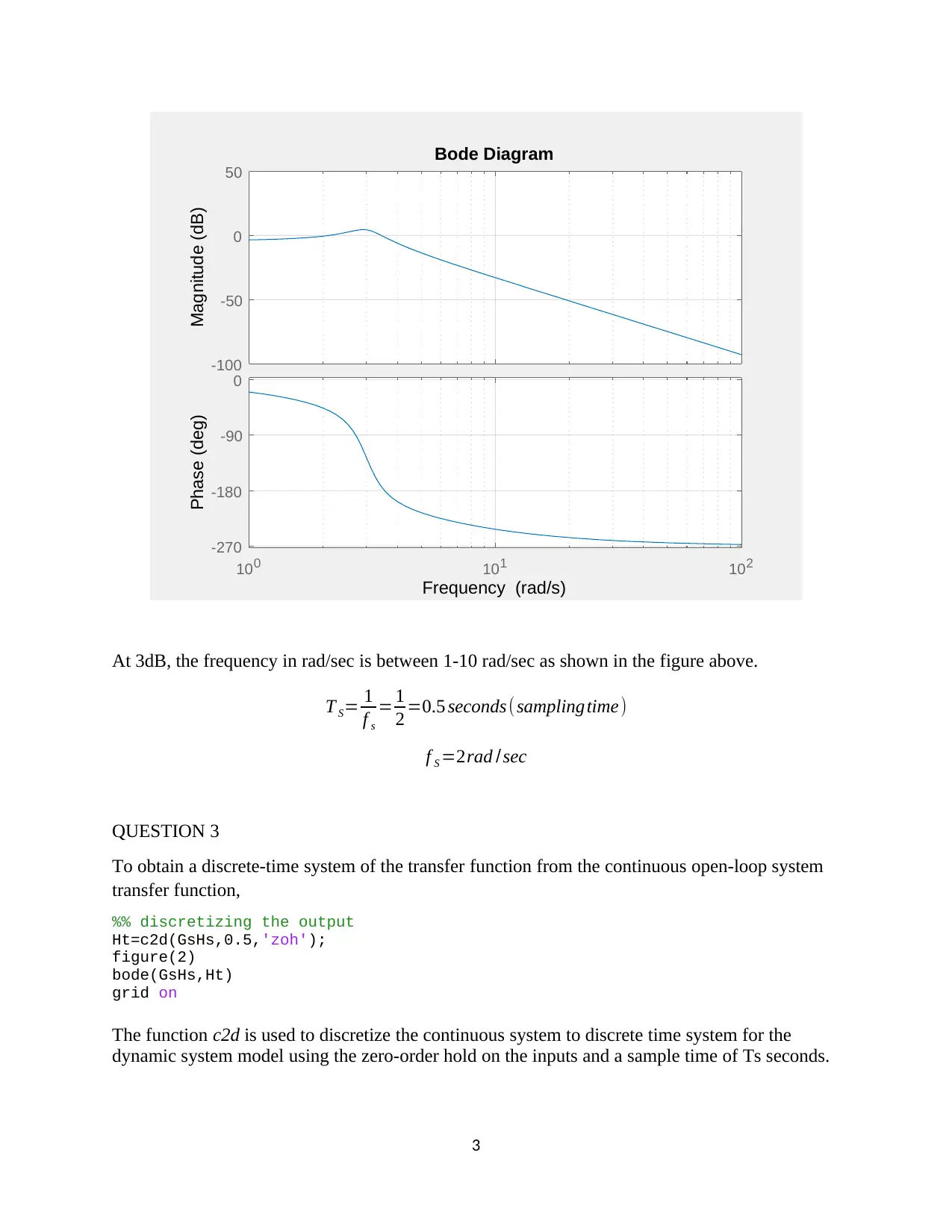
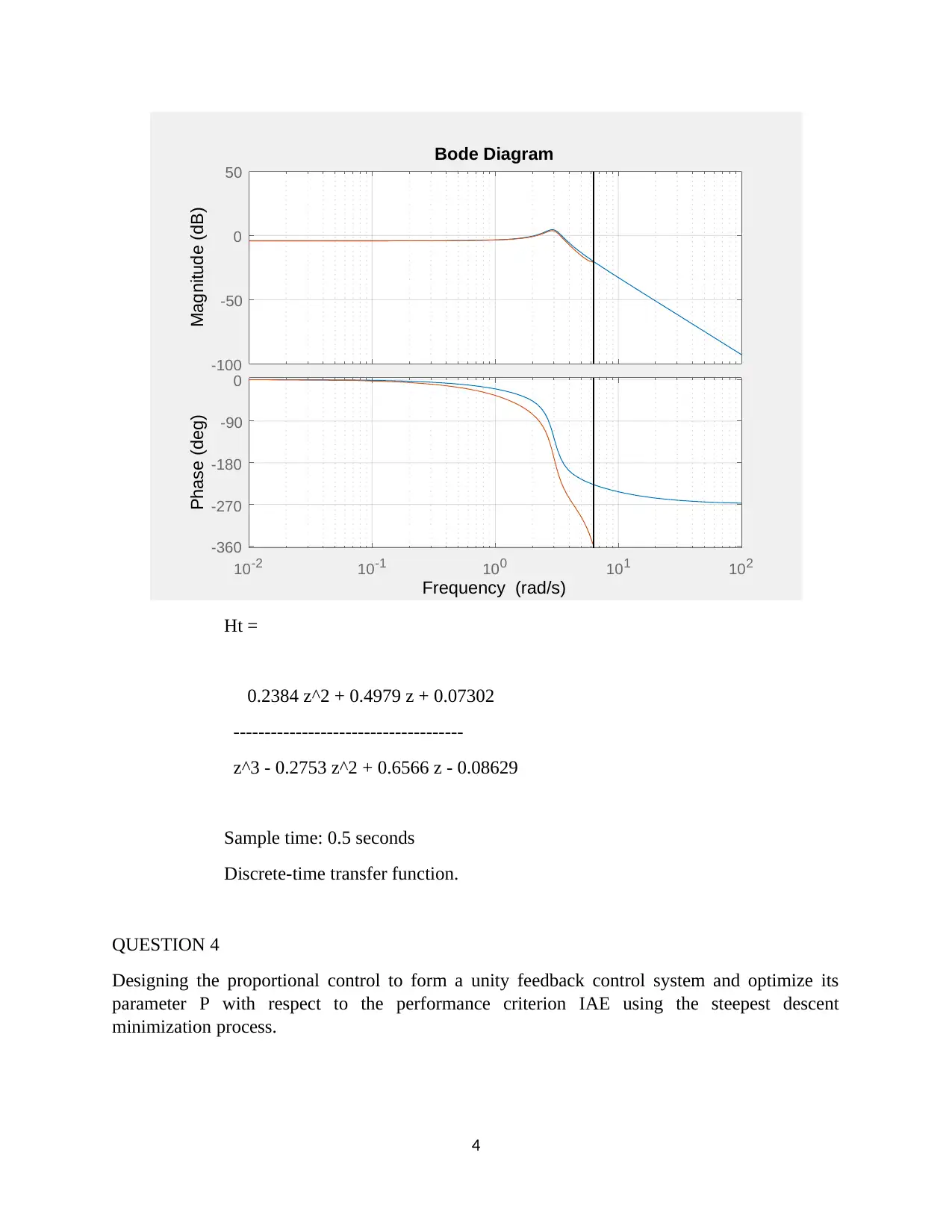
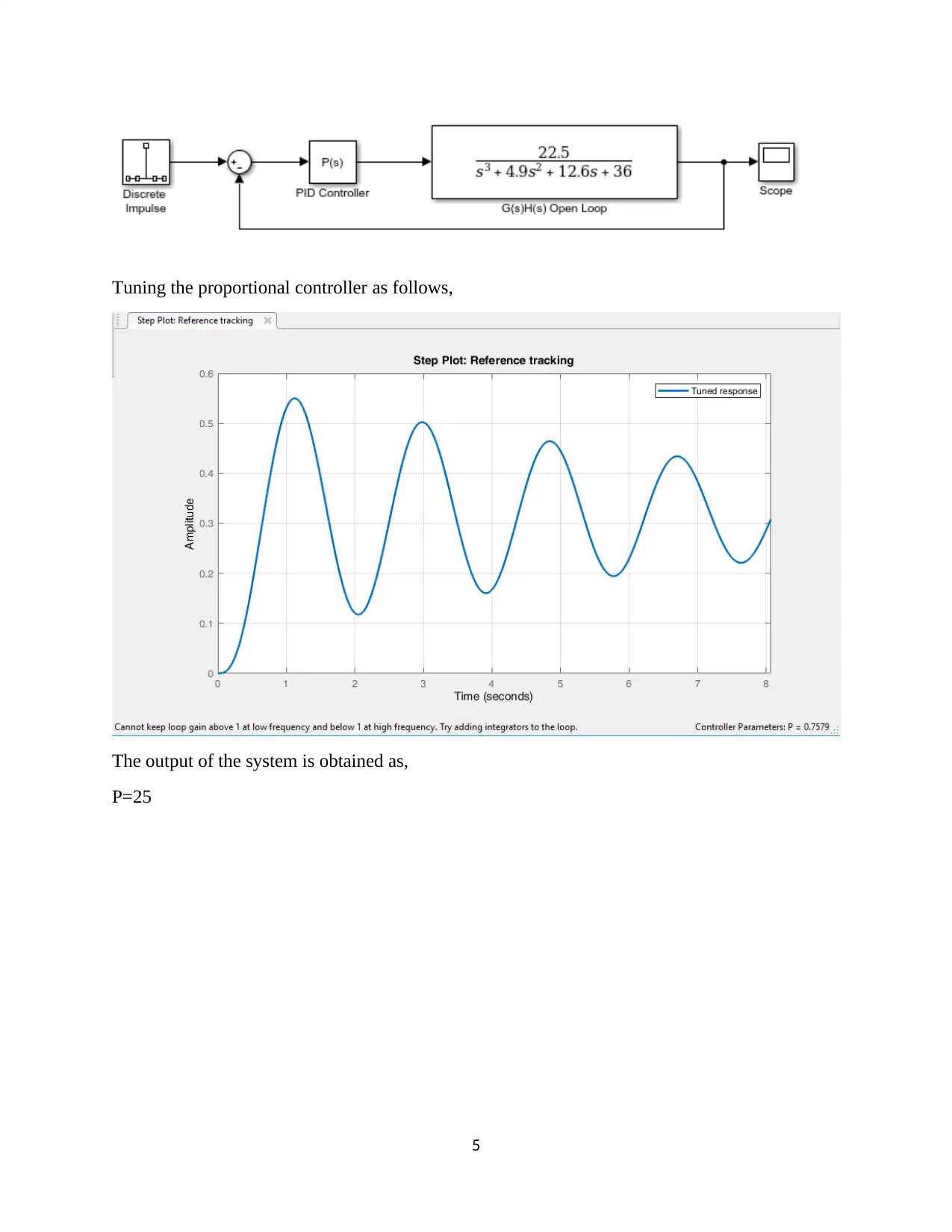
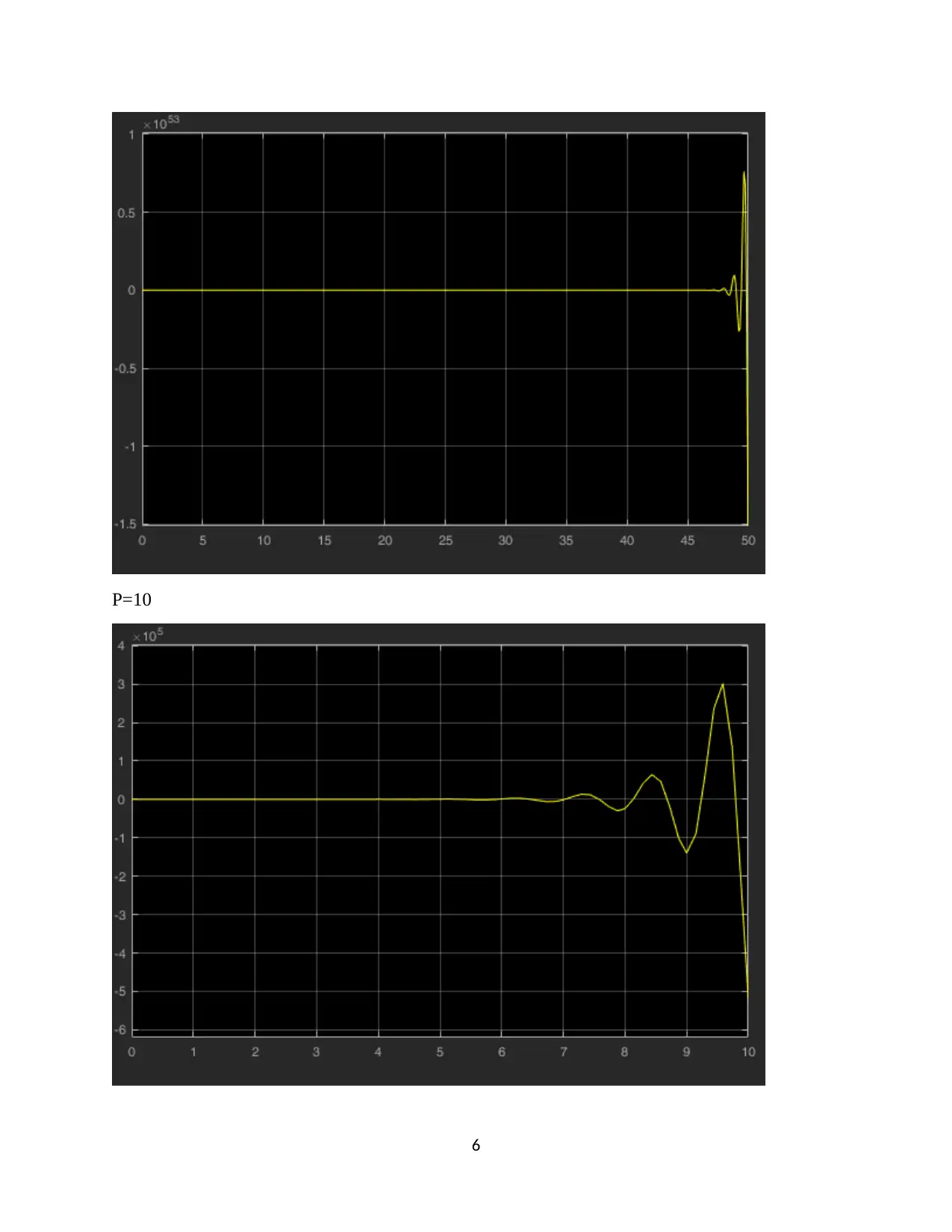
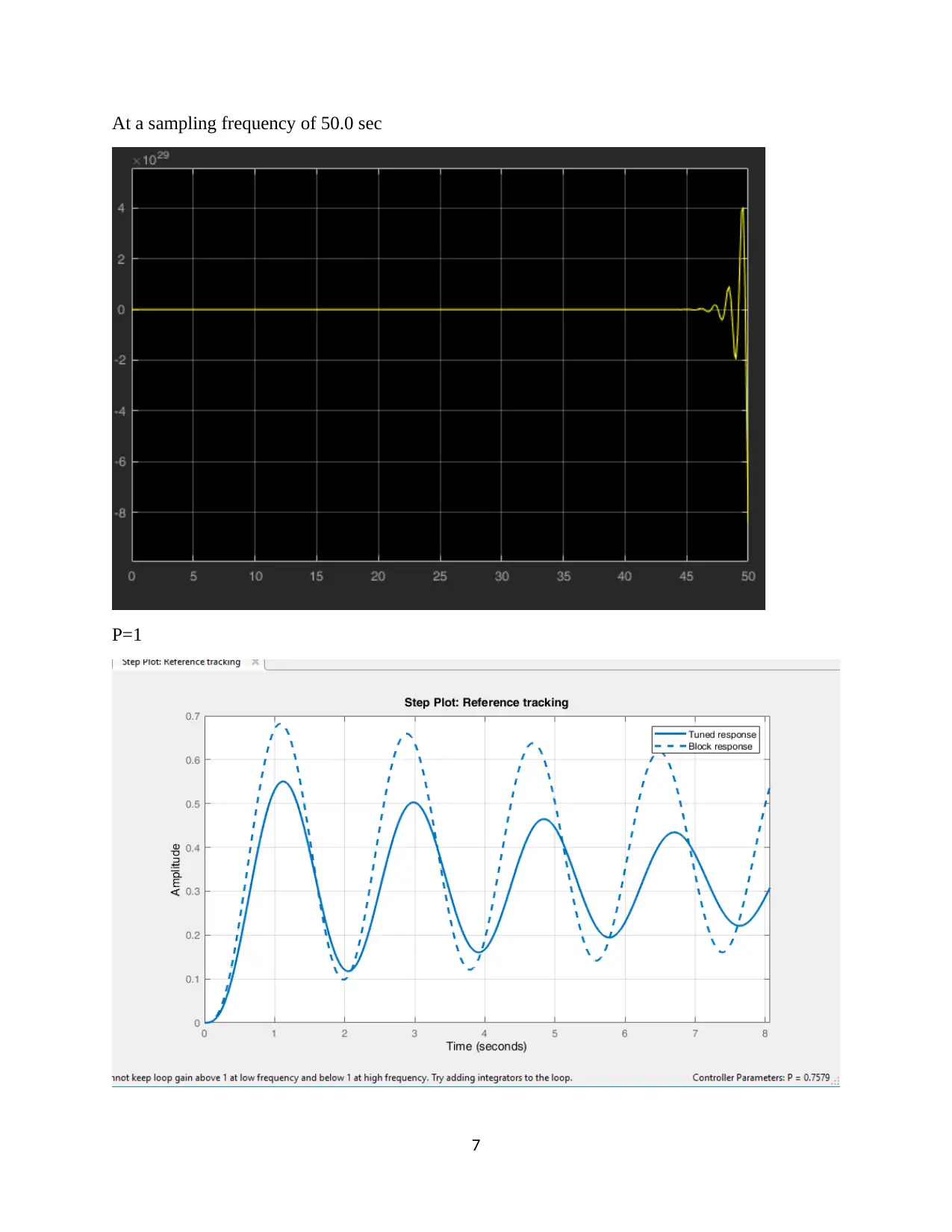
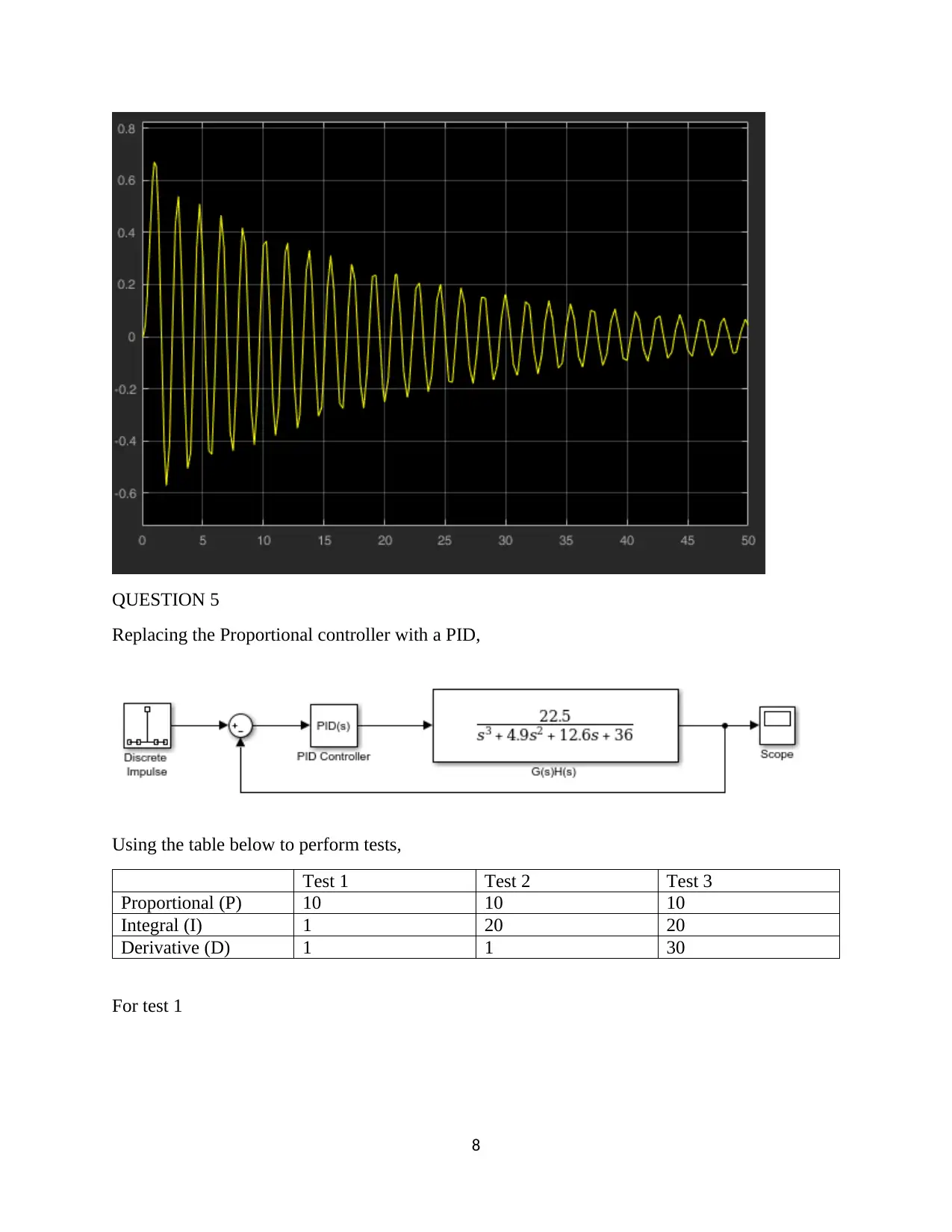
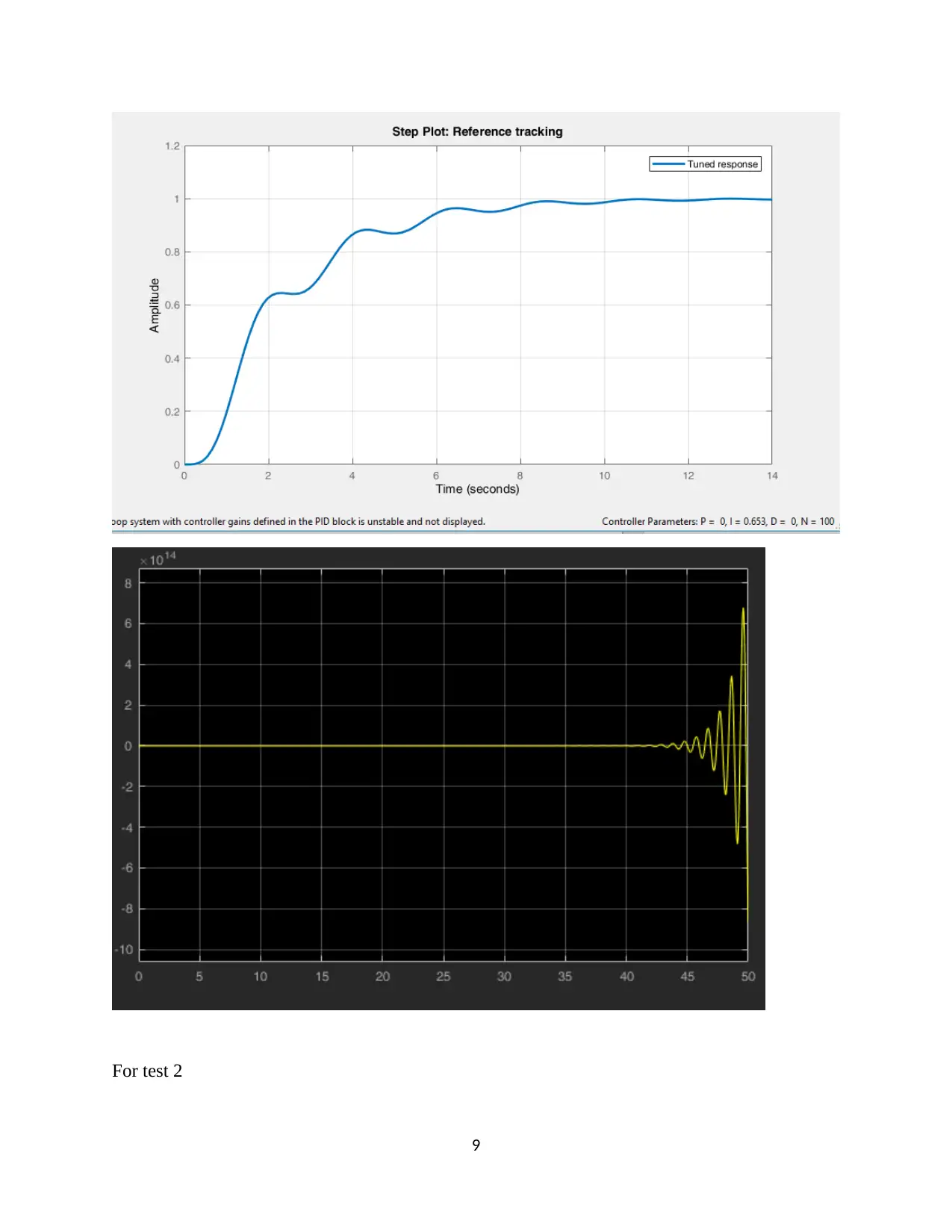
This assignment focuses on the design and analysis of a closed-loop roll stabilizing system for ships using digital control methods and MATLAB Simulink. The first question involves finding the open-loop response to a unit impulse input. The second question determines a suitable sample interval based on the sampling theorem and Bode plots. The third question derives the discrete-time system transfer function. The fourth question designs a digital proportional controller, and the fifth replaces it with a PID controller, tuning parameters for optimal performance. The second assignment involves designing a position control system with a power amplifier, motor, and load, simulating it in MATLAB, discretizing the system, selecting a proper sampling interval, designing a state variable feedback regulator, and implementing a dead-beat observer for state variable feedback. The solution provides detailed MATLAB code and simulation results for each part of the assignment.
1 out of 20








![[object Object]](/_next/static/media/star-bottom.7253800d.svg)