Solutions to Mathematical Problems

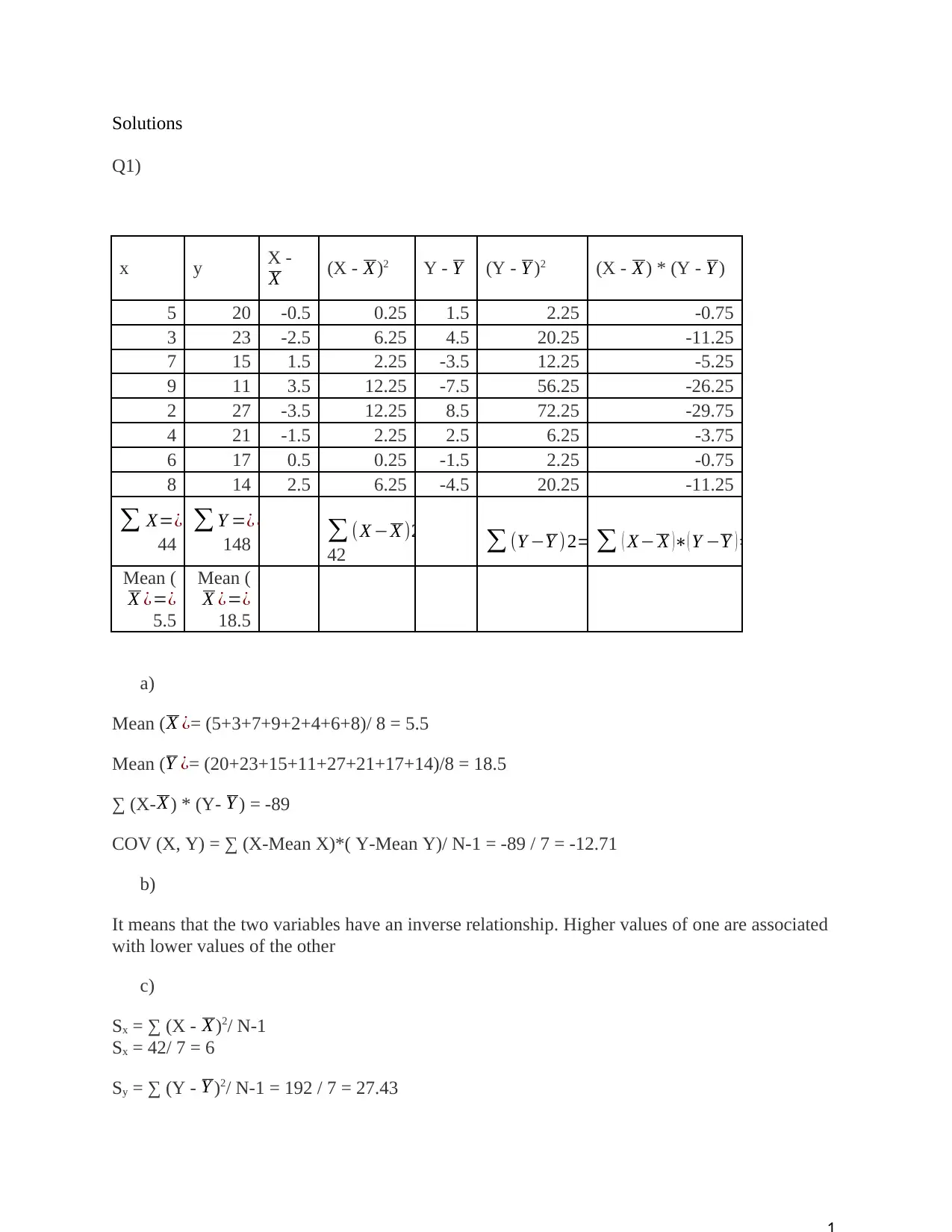
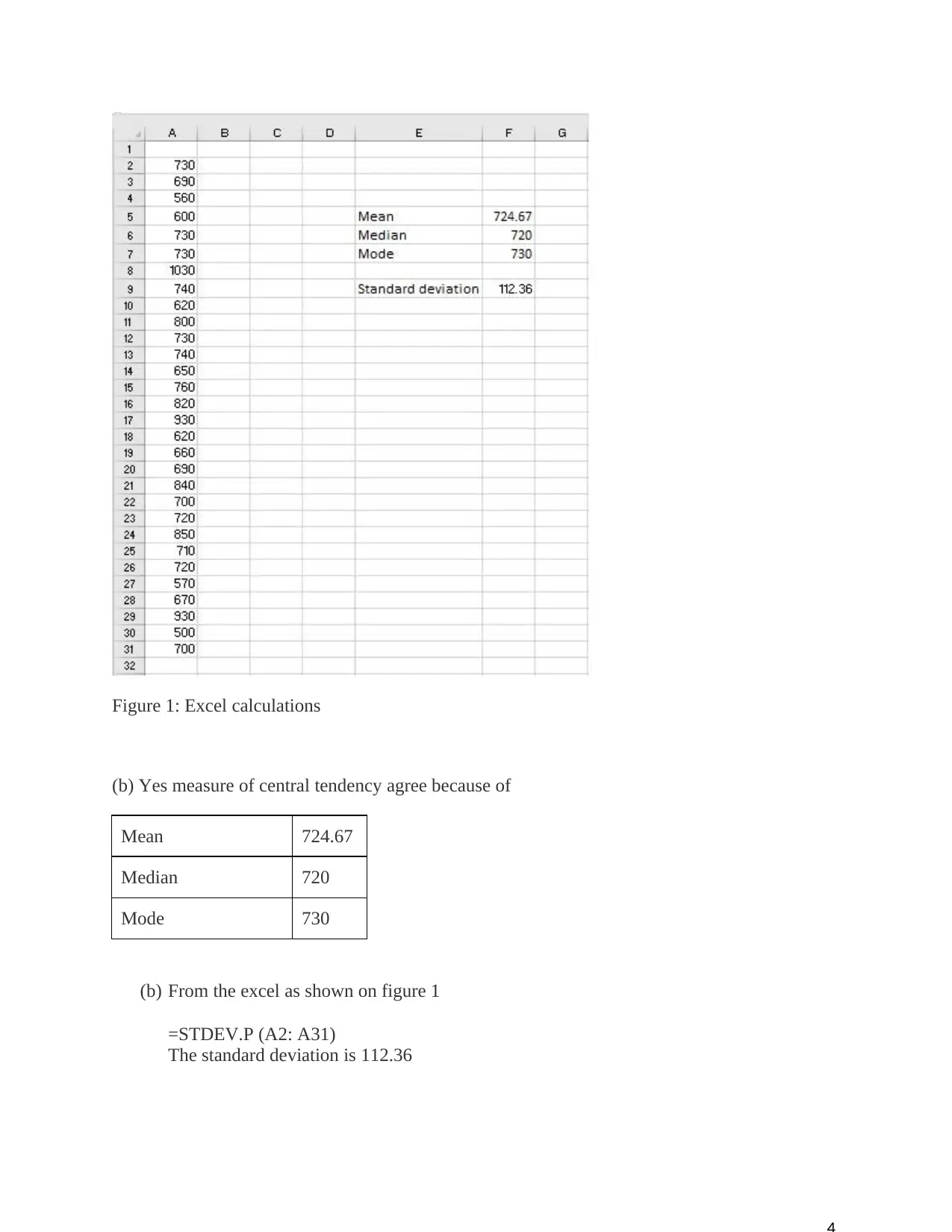
The text provides solutions to several mathematical problems. The first problem involves calculating the mean, median, mode, and standard deviation of a set of data using Excel. The second problem involves calculating the probability of a competitor being correct, given a null hypothesis and sample data. The third problem involves calculating the correlation coefficient between two variables, given their covariance and standard deviations. The fourth problem involves calculating the probability of a package being delivered on time, given the probabilities of it being delivered by three different carriers and the probabilities of each carrier delivering on time. The text also provides calculations for the probabilities of a package being delivered by each carrier, given that it was delivered on time or late.

Solutions
Q1)
x y X -
X (X - X )2 Y - Y (Y - Y )2 (X - X ) * (Y - Y )
5 20 -0.5 0.25 1.5 2.25 -0.75
3 23 -2.5 6.25 4.5 20.25 -11.25
7 15 1.5 2.25 -3.5 12.25 -5.25
9 11 3.5 12.25 -7.5 56.25 -26.25
2 27 -3.5 12.25 8.5 72.25 -29.75
4 21 -1.5 2.25 2.5 6.25 -3.75
6 17 0.5 0.25 -1.5 2.25 -0.75
8 14 2.5 6.25 -4.5 20.25 -11.25
∑ X=¿ ¿
44
∑ Y =¿ ¿
148 ∑ (X −X )2=¿ ¿
42 ∑ (Y −Y ) 2=¿ 192 ¿∑ ( X− X )∗( Y −Y )=−89
Mean (
X ¿=¿
5.5
Mean (
X ¿=¿
18.5
a)
Mean ( X ¿= (5+3+7+9+2+4+6+8)/ 8 = 5.5
Mean (Y ¿= (20+23+15+11+27+21+17+14)/8 = 18.5
∑ (X- X ) * (Y- Y ) = -89
COV (X, Y) = ∑ (X-Mean X)*( Y-Mean Y)/ N-1 = -89 / 7 = -12.71
b)
It means that the two variables have an inverse relationship. Higher values of one are associated
with lower values of the other
c)
Sx = ∑ (X - X )2/ N-1
Sx = 42/ 7 = 6
Sy = ∑ (Y - Y )2/ N-1 = 192 / 7 = 27.43

We got Sy = 6, Sy = 27.43
Cov(x, y) = -12.71
r(x, y) = Cov(x, y) / Sx * Sy
r(x, y) = -12.71 / 6*27.43 = -0.077
d)
Since the value of r(x, y) is negative so both X and y are negatively related with each other
Q2)
a) H0: P = 0.10
Ha: P ≠ 0.10
b) ^P = 81/900 = 0.09
Z =
p− ^p
√ p ( 1− p )
n
=
0.09−0.10
√ 0.10 ( 1−0.10 )
900
= -1
The P-value = 2 * P(Z < -1)
= 2 * 0.1587
= 0.3174
Since The P-value > ∝ = 0.05, so we should not reject H0.
So at 5% significance level there is enough evidence to infer that the competitor is correct.
c) For 95% confidence interval, the critical value z* = 1.96
The 95% confidence interval for population proportion is
^P +/- z* * √ P ( 1−P )
n

= 0.09 +/- 1.96 * √ 0.10 ( 1−0.10 )
900
= 0.09 +/- 0.0196
= 0.0704, 0.1096
d)
The values within the intervals of a 95% confidence will be considered acceptable, while values
that will be outside the intervals are always rejected. Therefore for the null hypothesis P = 0.10 is
contained in the 95% interval 0.0704 to 0.1096, this means that the null hypothesis will be
accepted at 0.05 level.
Q3)
(a) using excel to solve for the Measure of central tendency
For Mean use
= AVERAGE (A2:A31)
For median use
=MEDIAN (A2: A31)
For Mode use
=MODE (A2: A31).

Figure 1: Excel calculations
(b) Yes measure of central tendency agree because of
Mean 724.67
Median 720
Mode 730
(b) From the excel as shown on figure 1
=STDEV.P (A2: A31)
The standard deviation is 112.36

d) verifying the unusual data values or outliners
Base on Empirical rules criteria for detecting unusual observation and outliners. The
unusual observations are beyond X 2 s− ¿+ ¿¿ ¿ limit, while Outliners are X 3 s− ¿+¿¿ ¿
95.44% of the values should be in the range
X 2 s− ¿+¿¿ ¿ = 724.7 2∗ ¿− ¿+¿112.36 ¿ ¿ ¿
= 724.7 – 2*112.36, 724.7 + 2*112.36
= 499.98, 949.42
99.73% of the values should be in the range
X 3 s− ¿+¿¿ ¿ = 724.7 3∗ ¿− ¿+¿ 112.36¿ ¿ ¿
= 724.7 – 3*112.36, 724.7 + 3*112.36
= 387.62, 1061.78
e) Yes
Q4)
What we know? P(A)= 0.6
P(B)= 0.3 P(C)= 0.1
P(OIA)= 0.8
P(OIB)= 0.6
P(OIC)= 0.4
i) P(O|A) = P ¿ ¿
P(O A) is P)O and A)
P(O A ¿=P ( O| A )∗P( A)
= 0.8 * 0.6
= 0.48
ii) To calculate the probability that a package was delivered on time, we have to find P(
O∧ A ¿+ P ( O∧B ) + P(O∧C)
P(O A ¿=0.48
P(O B ¿=P ( O|B )∗P ( B )
= 0.6 * 0.3
= 0.18

P(O C ¿=P ( O|C ) ∗P(C)
= 0.4 * 0.1
= 0.04
Therefore, required probability = P(O A ¿+ P ( O B ) + P(O C)
= 0.48 + 0.18 + 0.04
= 0.7
iii) We have to find P(A|O) for this, we will use Baye’s theorem
P(A|O) = P ( O|A )∗P ( A )
P ( O|A )∗P ( A ) + P (O|B )∗P ( B ) + P ( O|C )∗P C
= 0.48
0.48+0.18+0.04
= 0.48
0.7
= 0.6857
iv) Let O be the event that the delivery was late
P(B|O) = 1 – P(B|O)
= 1 - P ( O|B ) ∗P (B)
P ( O| A )∗P ( A ) + P ( O|B ) ∗P ( B ) +P ( O|C )∗PC
= 1 - 0.18
0.7
= 0.7429
v)
P(C|O) = 1 – P(C|O)
= 1 - P ( O|C ) ∗P (C)
P ( O| A )∗P ( A ) + P ( O|B ) ∗P ( B ) +P ( O|C )∗PC
= 1 - 0. 04
0.7
= 0.9429