Mechanical Engineering Principles: Case Study Analysis and Solutions

This document presents a comprehensive Mechanical Engineering case study, addressing various mechanical engineering principles through detailed analysis and solutions. The case study covers topics such as beam analysis, including the calculation of reaction forces, shear force diagrams, and bending moment diagrams. It delves into the properties of beams, different types of loadings, and beam classifications. Furthermore, the assignment explores concepts related to centripetal acceleration in space stations, the advantages of counter-rotating cylinders for sunlight harvesting, and calculations related to buoyancy forces and cargo capacity of barges. The document also examines pressure calculations at different depths and the need for ballast tanks in platform systems. Excel calculations are included to support the analysis. The assignment provides a practical application of mechanical engineering principles to solve real-world problems. This assignment is a valuable resource for students seeking to understand and apply mechanical engineering concepts.

MECHANICAL Project

Table of Contents
1. Case Study A...........................................................................................................................2
1.1 Question 1.........................................................................................................................2
1.2 Overview of the Beam......................................................................................................4
2. Case Study B............................................................................................................................7
2.1 Question 1.........................................................................................................................7
2.2 Question 2.........................................................................................................................8
2.3 Question 3.........................................................................................................................8
3. Case study C..........................................................................................................................11
3.1 Question 1.......................................................................................................................11
3.2 Question 2.......................................................................................................................13
4. Case study D..........................................................................................................................15
4.1 Question 1.......................................................................................................................15
4.2 Question 2.......................................................................................................................16
4.3 Question 3.......................................................................................................................17
5. References..............................................................................................................................18
6. Appendix................................................................................................................................19
1

1. Case Study A
1.1 Question 1
a) Reaction forces
Here, summation of horizontal forces are zero and summation of moments are zero.
Take moment about point A and point B.
Calculate RD and RA
Reaction force at point A, (RA) = 82.5 kN.
Reaction force at point D, (RD) = 77.50 kN.
Here, summation of vertical forces are zero.
Find the shear force at Point A, B, C and D (QA, QB, QC, and QD)
2

After that, find the bending moment at Point A, B, C and D (MA, MB, MC, and MD)
The calculations are added in appendix.
b) Shear force diagram
It is given in below diagram.
c) Bending moment diagram
The shear force and bending moment diagrams are shown below.
3

d) Max S.F and B.M
From the calculation done, the maximum shear force value and the maximum bending
moment value is found.
Maximum shear force value = 82.5 kN.
It acts at the point “A”.
Maximum Bending Moment value = 85 kN.m.
It is found in Point “C”.
1.2 Overview of the Beam
What is Beam?
Beam is a mechanical element. It is used to support the loads. Mostly it has a horizontal
orientation, in some cases we can see this at an inclined positions. In general, vertical loads and
moments are act on this element. And in some rare cases horizontal loads also may act on this
element. In other words, beam is a structural element. Its length is higher than its cross-sectional
dimensions like width and thickness. Also it undergoes to the lateral loading (Zhang et al. 2014).
Types of Beams
Beams are classified by many factors like type of support, Cross section etc. But
generally beams are classified according to the type of support used. In this section, the brief
overview of all five types of beams are shown.
Type Diagram Commercial
Application.
Cantilever Beam Aircraft wings,
& Balcony
support
4

Simply
Supported Beam
Bridges
Continuous
Beam
Bridges
Fixed Beam Rigid Structural
elements
Over hanging
Beam
Balcony
Types of loadings
Type Diagram
Point load
Uniformly Distributed Load
Uniformly varying load
Bending moment diagram and Shear force diagram shape
In this section, the Bending moment diagram and Shear force diagram shapes are drawn
for various types of loads acts on the various types of Beams.
5

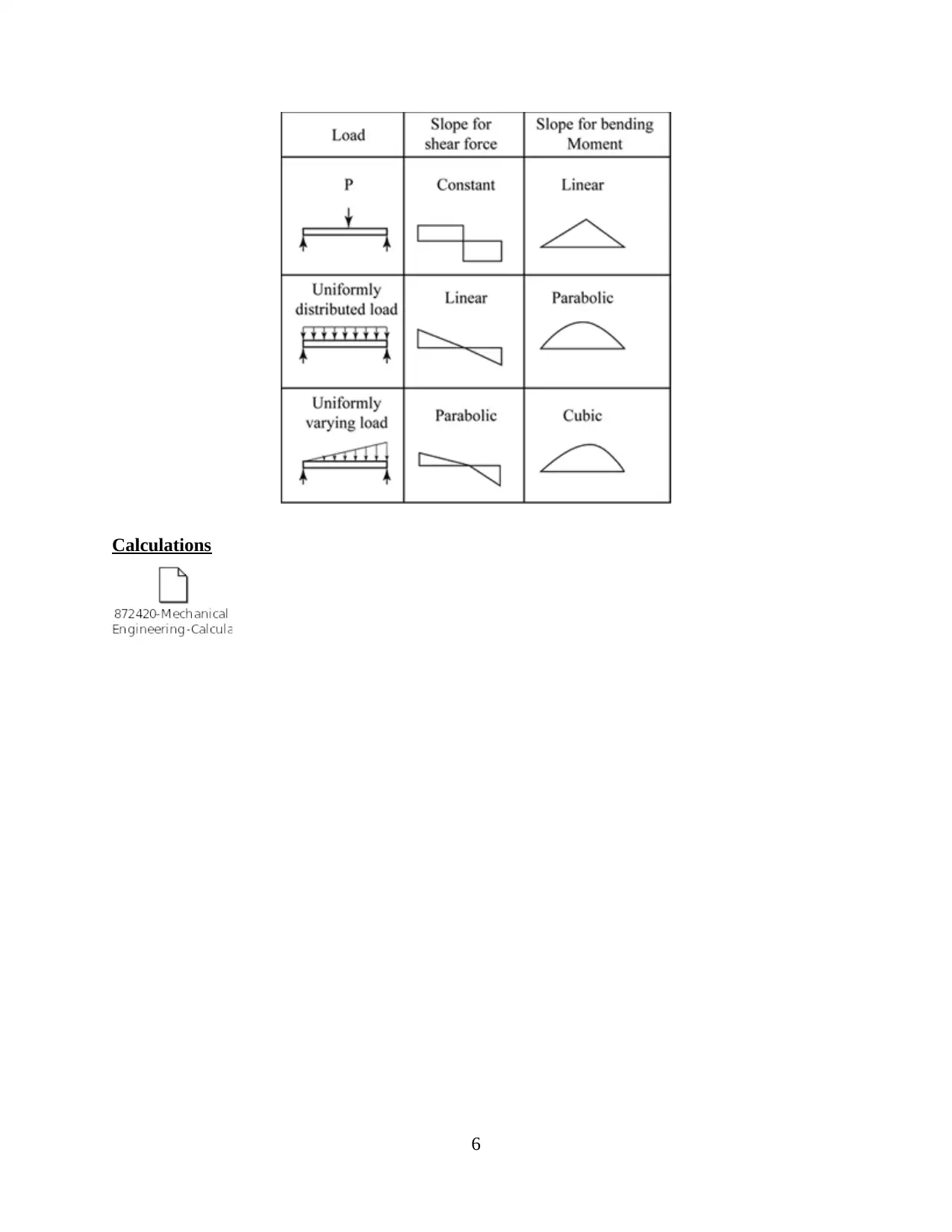
Calculations
6

2. Case Study B
2.1 Question 1
a) Finding speed for developing the gravity
In this kind of space stations, the centripetal force developed by the rotary motion acts similar to
the gravitational pull.
So
Here the r= 0.9 km or 900 m
Centripetal acceleration a = 9.81 m/s2
According to this formula, the ring must rotate at 1 rpm in counter clockwise direction to
develop the centripetal acceleration as 9.81 m/s2.
Here, w= (2*pi*N)/60.
Using this, N value is found.
The calculation for this is added in appendix.
7

2.2 Question 2
Best place for constructing the zero gravity lab is its center. Because the center of the
space station has the zero centripetal force.
Because the acceleration due to centripetal force,
At center, r = 0.
Applying r = 0 to the formula. Then, the acceleration value is zero (a=0).
This calculation is added in appendix.
2.3 Question 3
8

a) Advantages of having two counter rotating cylinders.
This design is proposed, because this design allows to get the sunlight constantly. In space
stations, the sun light is the one and only source for developing energy for various purposes
(Kamisaka 2001). So this design helps to reduce the complications involved in the energy
extraction from the sun. And another important thing it avoids other gyroscopic effects.
b) Required speed for develop the acceleration 9.81 m/s2
Here,
Radius r = 8 km
Length L = 32 km
And w= (2*pi*N)/60.
According to this formula, the cylinder must rotate at 0.33 rpm in counter clockwise direction to
develop the centripetal acceleration as 9.81 m/s2.
The N value is 0.33 rpm.
This calculation is added in appendix.
Calculations
9

3. Case study C
3.1 Question 1
Here, the initial load is 450 kN.
i) Given, Original area (Ad)= 35 m2
Find area (Aa)?
Formula:
Buoyancy force= volume of submerged portion of barge * density of water *
gravitational force. (GROBARCIKOVA and SOSEDOVA 2016)
10

Using this formula, the Area (Aa) is calculated. Area (Aa) is 32.63 m2.
This calculation is added in appendix
ii) Here, maximum weight of cargo barge can carry (t) = 2.0 m
Formula used here is Wwave= Aa* t*998*9.81
Using this formula, Wwave value is calculated.
This calculation is added in appendix.
iii) Here for float on surface of water (l) = 3 w
Answer
11