MEng Numerical Solutions of Partial Differential Equations Assignment
VerifiedAdded on 2023/01/23
|10
|1396
|83
Practical Assignment
AI Summary
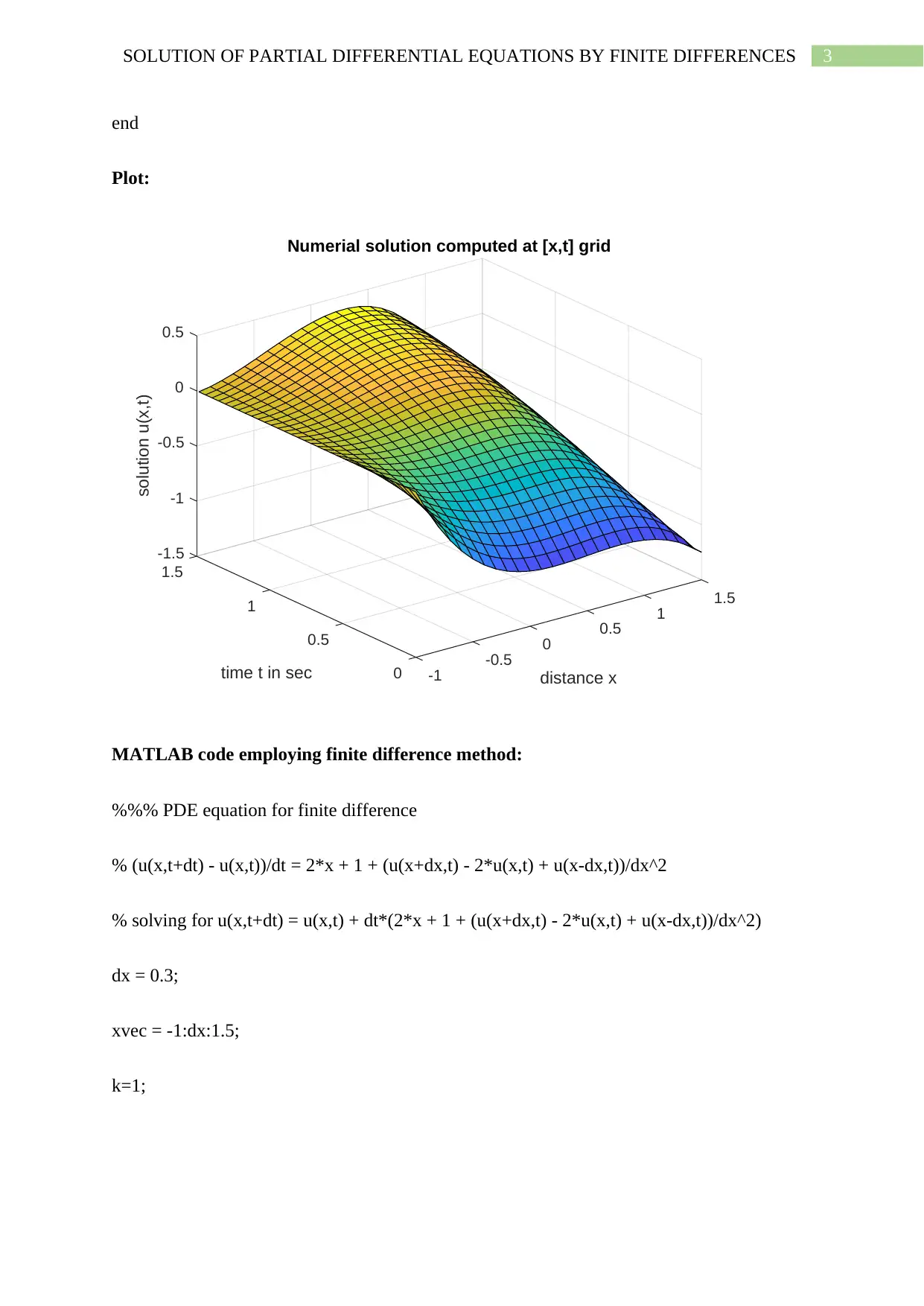
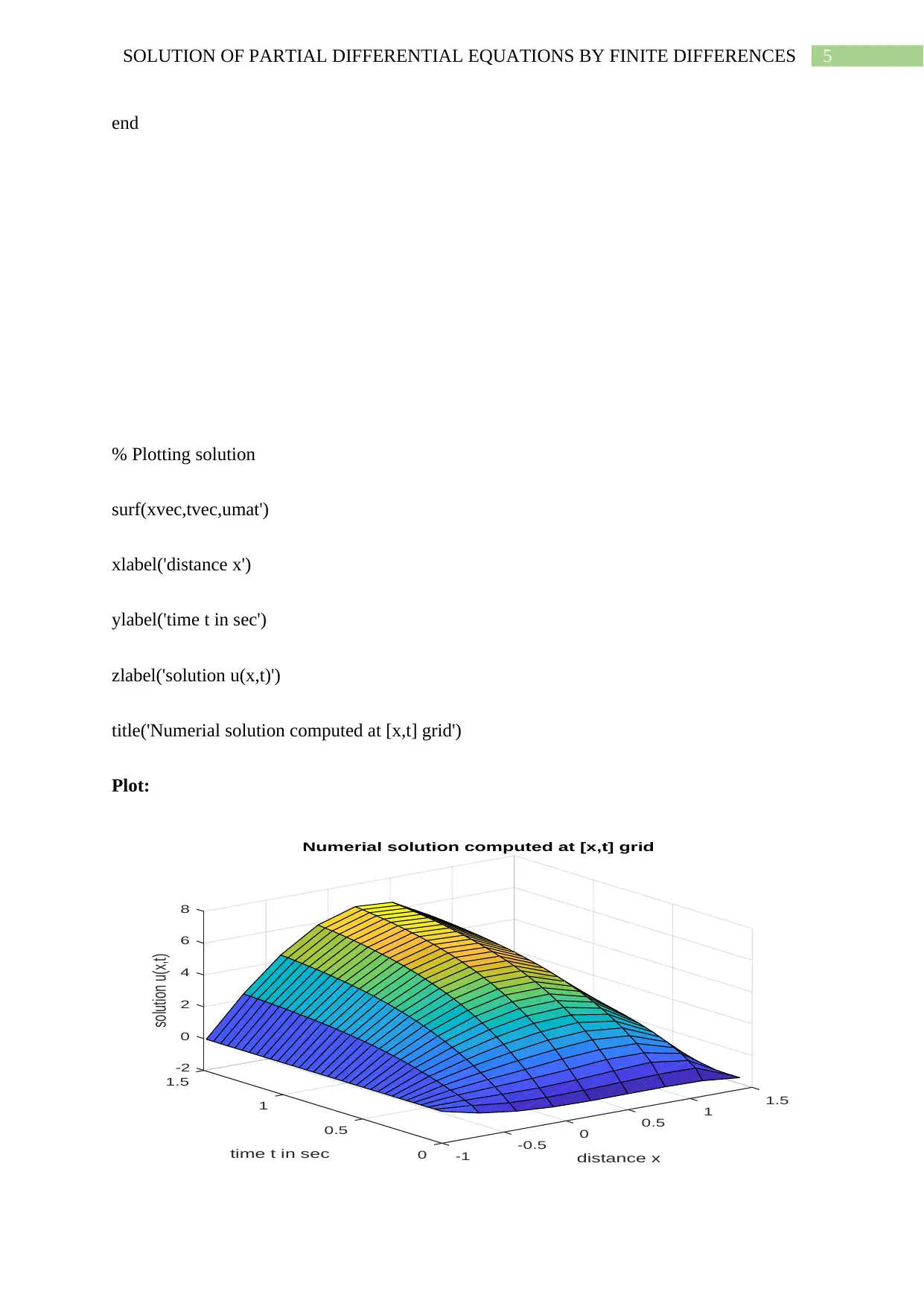
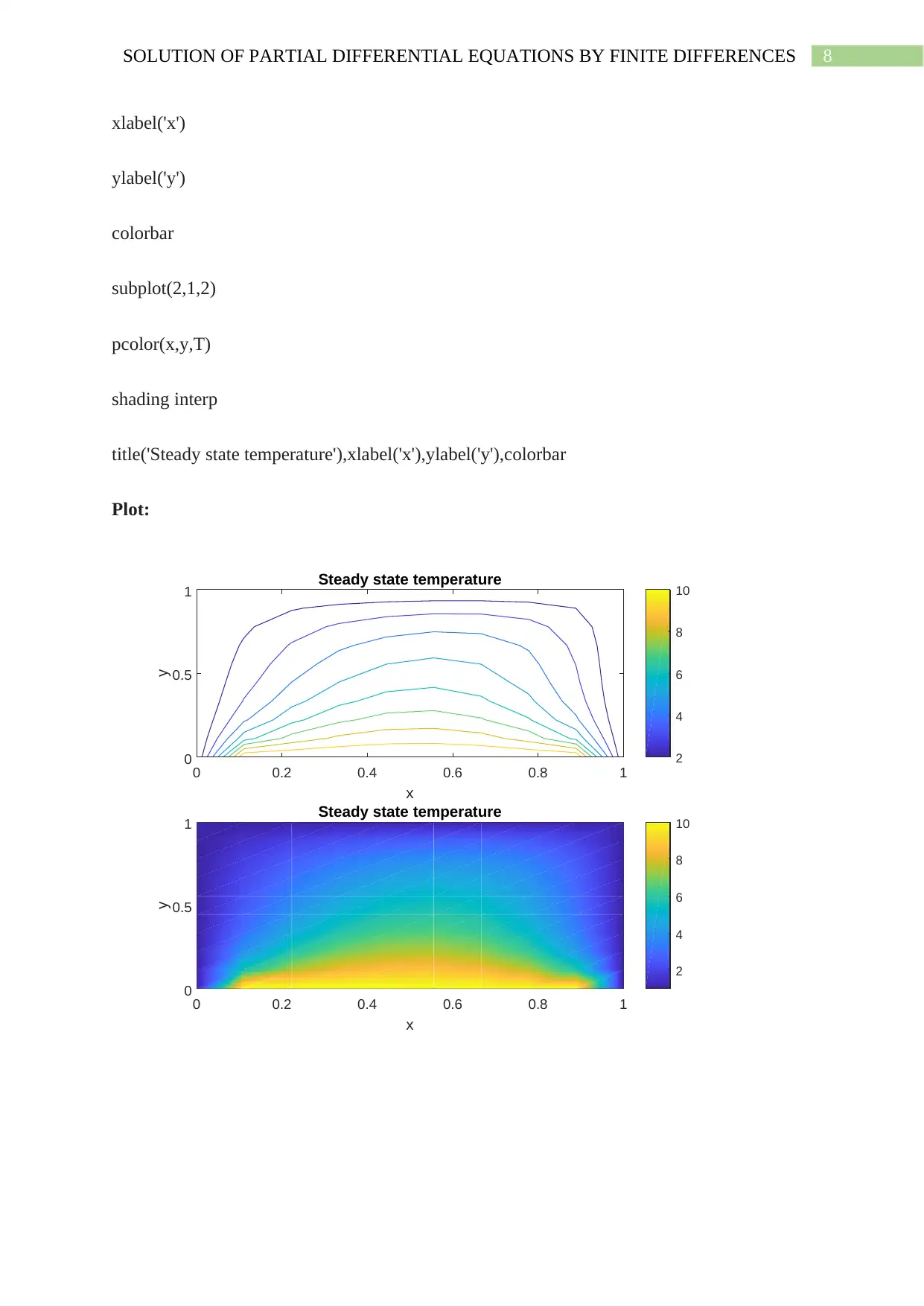
This assignment presents solutions to partial differential equations (PDEs) using the finite difference method implemented in MATLAB. The first part addresses a 1D PDE, providing MATLAB code using both the built-in `pdepe` function and a custom finite difference implementation. It includes initial and boundary conditions, along with plots of the numerical solutions. The second part extends the approach to a 2D heat equation, also solved using the finite difference method in MATLAB. The assignment covers setting up the problem, defining the grid, applying boundary conditions, and iteratively solving for the temperature distribution until a steady state is reached. Contour and pcolor plots are included to visualize the steady-state temperature distribution. The assignment demonstrates the practical application of finite difference methods for solving PDEs and provides detailed MATLAB code and plots for each problem.
1 out of 10














![[object Object]](/_next/static/media/star-bottom.7253800d.svg)