Probability Assignment | Answers

Surname 1
Name:
Instructor:
Course:
Date:
Question 1
p ( t ) =P. of transfering a ball
p ( t ) = r1
n1
p ( g ) =P . of picking green ball ¿ urn 2after transfering a ball= r2
n2 +1
Therefore
probability of picking a green ball= ( r1
n1 )× ( r 2
n2+1 )= r1 r 2
n1 (n2 +1)
Question 2
a.
For probability mass function (pmf);
∑ p ( xi ) =1
p ( xi )>0
f ( x )= x +2
c , x=1,2,3 , … … … 15
So ∑ p ( xi ) =1 50
150
C =1
C=150

Surname 2
b.
Number of copies sold in a year
∑ p ( xi ) =150
150 Copies
c.
Profit for the year
Profit from each book is $10. So total profit;
Total profit=$ 10 ×150
Total profit=$ 1500
Question 3
The exponential function , f ( x )=λ e− λ x
λ= 1
15 =0.067
p ( x>12 ) =0.067 e−0.067(12)
p ( x>12 ) =0.03
Question 4
a. Two standard deviation about the mean of 10 is 9.8
p ( x ; μ )= e− λ λx
x !
p ( 9.8 ; 10 )= e−10 1010
10 !
p ( 9.8 ; 10 )=0.125
b.
p ( x ; μ )= e− λ λx
x !
p ( 5 ;10 )= e−10 105
5 !

Surname 3
p ( 5 ;10 )=0. 038
c.
p ( x ; μ )= e− λ λx
x !
p ( 10.67 ;10 )= e−10 1010.67
10.67 !
p ( 10.67 ; 10 )=0.0 .12
Question 5
a.
Sample proportion
proportion= 0.0915+ 0.3085
2 =0.2
proportion=0.2
b.
margin of error=0.3085−0.2
margin of error=0.1085
But
margin of error=zα /2 √ ^p ( 1− ^p )
n
0.1085=zα/ 2 √ 0.2 ( 1−0.2 )
50
0.1085=zα/ 2 √ 0.2 ( 0.8 )
50
0.1085=zα/ 2( 0.0565685)
zα/ 2= 0.1085
0.0565685
zα/ 2=1.92

Surname 4
From the standard normal table, β=95 %
c.
The least number of graduates;
0.0195 ×50=1 student
Question 6
a. Hypothesis
H0: μ1 - μ2 = 0
H1 : μ1−μ2 ≠ 0
b. Rejection region
c. Test
Z0= x1−x2
√ σ1
2
n1
+ σ2
2
n2
Z0= 69−64
√ 284
54 + 208
51
Z0= 5
3.05576 =3.0558
Rejection region
α/2=0.025α/2=0.025

Surname 5
P-value corresponding to a Z- value of 3.0558 (two-tailed, 0.05) is 0.002. Since p< 0.05, the null
hypothesis is rejected. It is concluded that there is a difference in the mean scores for the
population associated with the two teaching methods.
Question 7
a.
Hypothesis
H0: There is no difference in the time taken to fall asleep before and after taking insomniac pills.
H1: There is a significant difference in the time taken to fall asleep before and after taking
insomniac pills.
Alpha = 0.01
b.
Rejection region
c.
Results
Paired Samples Test
Paired Differences t df Sig. (2-
tailed)Mean Std.
Deviation
Std. Error
Mean
95% Confidence Interval of
the Difference
Lower Upper
Pair 1 no_pill -
with_pill
21.60000 8.79204 3.93192 10.68324 32.51676 5.493 4 .005
Table 1
Since the p-value obtained (0.005) is less than the significance level (0.05), the null hypothesis is
rejected and the alternative accepted. The conclusion is that there is a significant difference in the
Rejection region
α/2=0.005α/2=0.005

Surname 6
time taken to fall asleep before and after taking insomniac pills. This in turn means that the
sleeping pills are effective.
Question 8
a.
Hypothesis
H0: μ1= μ2= μ3= μ4
H1: At least one method has a different mean.
Alpha = 0.05
b.
Rejection region
c.
Result
ANOVA
Source of
Variation SS df MS F P-value F crit
Between Groups
449.557
9 3
149.852
6
3.78670
7
0.03328
2
3.28738
2
Within Groups 593.6 15
39.5733
3
Total
1043.15
8 18
Table 2
Rejection region
α/2=0.025α/2=0.025

Surname 7
Since the p-value obtained (0.03) is less than the significance level (0.05), the null hypothesis is
rejected and the alternative accepted. The conclusion is that at least one method had a
significantly different mean.
Question 9
a.
Hypothesis
H0: There is no association between the level of Angina and the level of coronary artery
obstruction.
H1: There is an association between the level of Angina and the level of coronary artery
obstruction.
Alpha = 0.05
b.
c.
Chi-square test results
Pearson Chi-Square = 8.276, DF = 6, P-Value = 0.219
Likelihood Ratio Chi-Square = 8.335, DF = 6, P-Value = 0.215
Since the p-value obtained (0.219) is less than the significance level (0.05), the null hypothesis is
not rejected. The conclusion is that there is no association between the level of Angina and the
level of coronary artery obstruction.
Rejection region
α/2=0.025α/2=0.025

Surname 8
Question 10
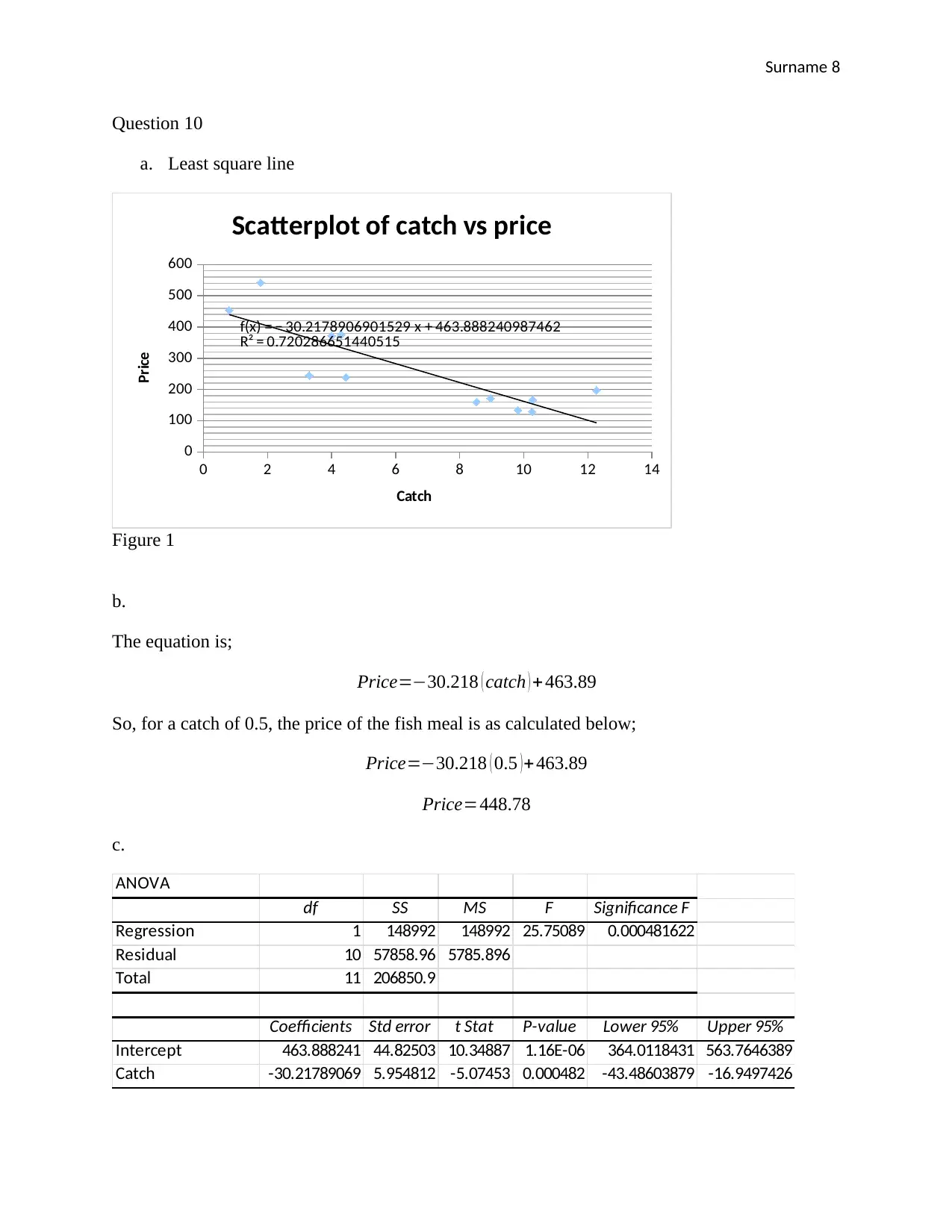
a. Least square line
0 2 4 6 8 10 12 14
0
100
200
300
400
500
600
f(x) = − 30.2178906901529 x + 463.888240987462
R² = 0.720286651440515
Scatterplot of catch vs price
Catch
Price
Figure 1
b.
The equation is;
Price=−30.218 ( catch ) + 463.89
So, for a catch of 0.5, the price of the fish meal is as calculated below;
Price=−30.218 ( 0.5 ) +463.89
Price=448.78
c.
ANOVA
df SS MS F Significance F
Regression 1 148992 148992 25.75089 0.000481622
Residual 10 57858.96 5785.896
Total 11 206850.9
Coefficients Std error t Stat P-value Lower 95% Upper 95%
Intercept 463.888241 44.82503 10.34887 1.16E-06 364.0118431 563.7646389
Catch -30.21789069 5.954812 -5.07453 0.000482 -43.48603879 -16.9497426

Surname 9
The value of the significance F (0.00) is less than the level of significance (0.01). This means
that the data presents sufficient evidence to indicate that the size of the anchovy catch contributes
information for the prediction of price of fish meal at 0.01 level of significance.