Probability and Statistical Analysis Graded Assignment Solutions

This article provides solutions to Probability and Statistical Analysis graded assignments. It covers topics such as normal distribution, probability, variance, sample size, and more. Each question is explained in detail with step-by-step calculations.

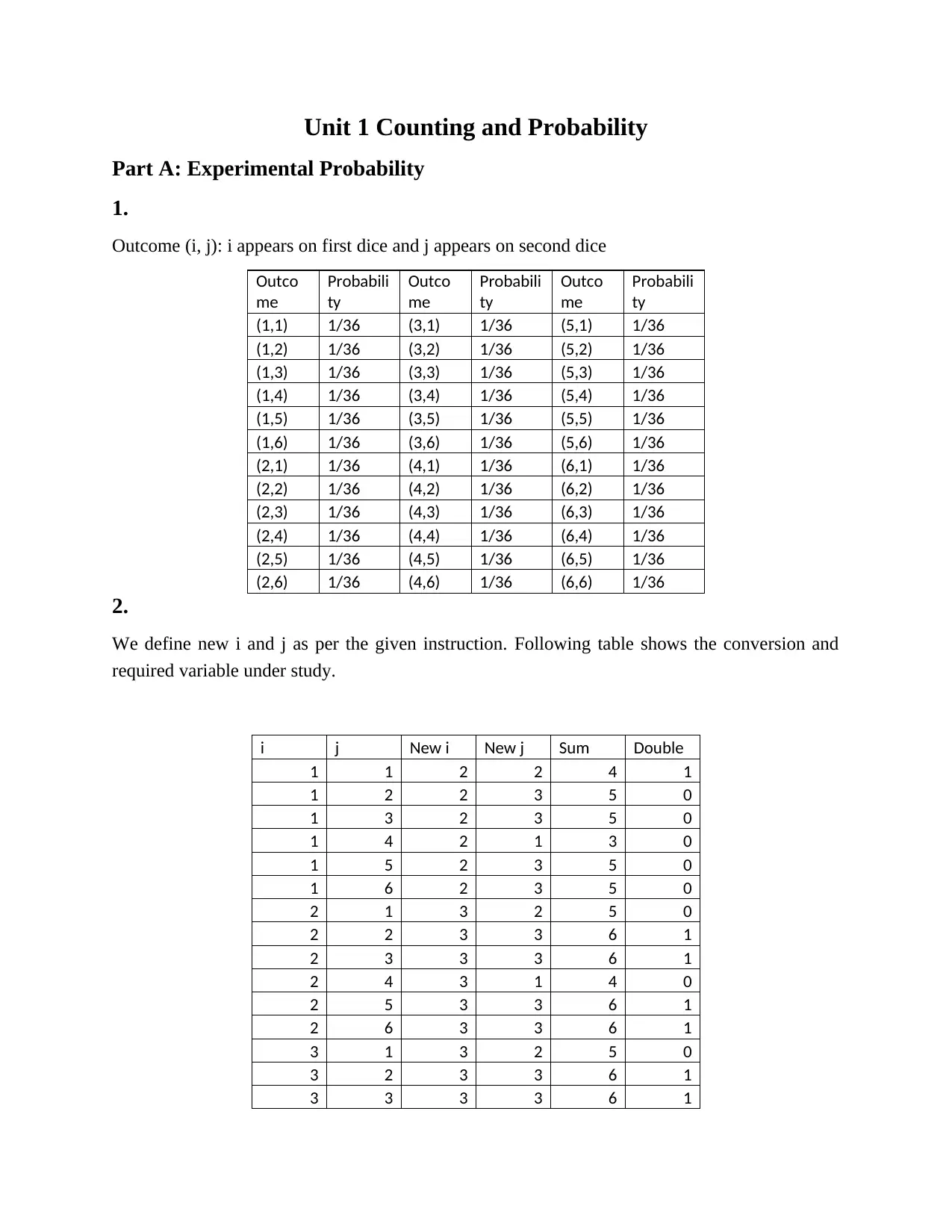
Unit 1 Counting and Probability
Part A: Experimental Probability
1.
Outcome (i, j): i appears on first dice and j appears on second dice
Outco
me
Probabili
ty
Outco
me
Probabili
ty
Outco
me
Probabili
ty
(1,1) 1/36 (3,1) 1/36 (5,1) 1/36
(1,2) 1/36 (3,2) 1/36 (5,2) 1/36
(1,3) 1/36 (3,3) 1/36 (5,3) 1/36
(1,4) 1/36 (3,4) 1/36 (5,4) 1/36
(1,5) 1/36 (3,5) 1/36 (5,5) 1/36
(1,6) 1/36 (3,6) 1/36 (5,6) 1/36
(2,1) 1/36 (4,1) 1/36 (6,1) 1/36
(2,2) 1/36 (4,2) 1/36 (6,2) 1/36
(2,3) 1/36 (4,3) 1/36 (6,3) 1/36
(2,4) 1/36 (4,4) 1/36 (6,4) 1/36
(2,5) 1/36 (4,5) 1/36 (6,5) 1/36
(2,6) 1/36 (4,6) 1/36 (6,6) 1/36
2.
We define new i and j as per the given instruction. Following table shows the conversion and
required variable under study.
i j New i New j Sum Double
1 1 2 2 4 1
1 2 2 3 5 0
1 3 2 3 5 0
1 4 2 1 3 0
1 5 2 3 5 0
1 6 2 3 5 0
2 1 3 2 5 0
2 2 3 3 6 1
2 3 3 3 6 1
2 4 3 1 4 0
2 5 3 3 6 1
2 6 3 3 6 1
3 1 3 2 5 0
3 2 3 3 6 1
3 3 3 3 6 1

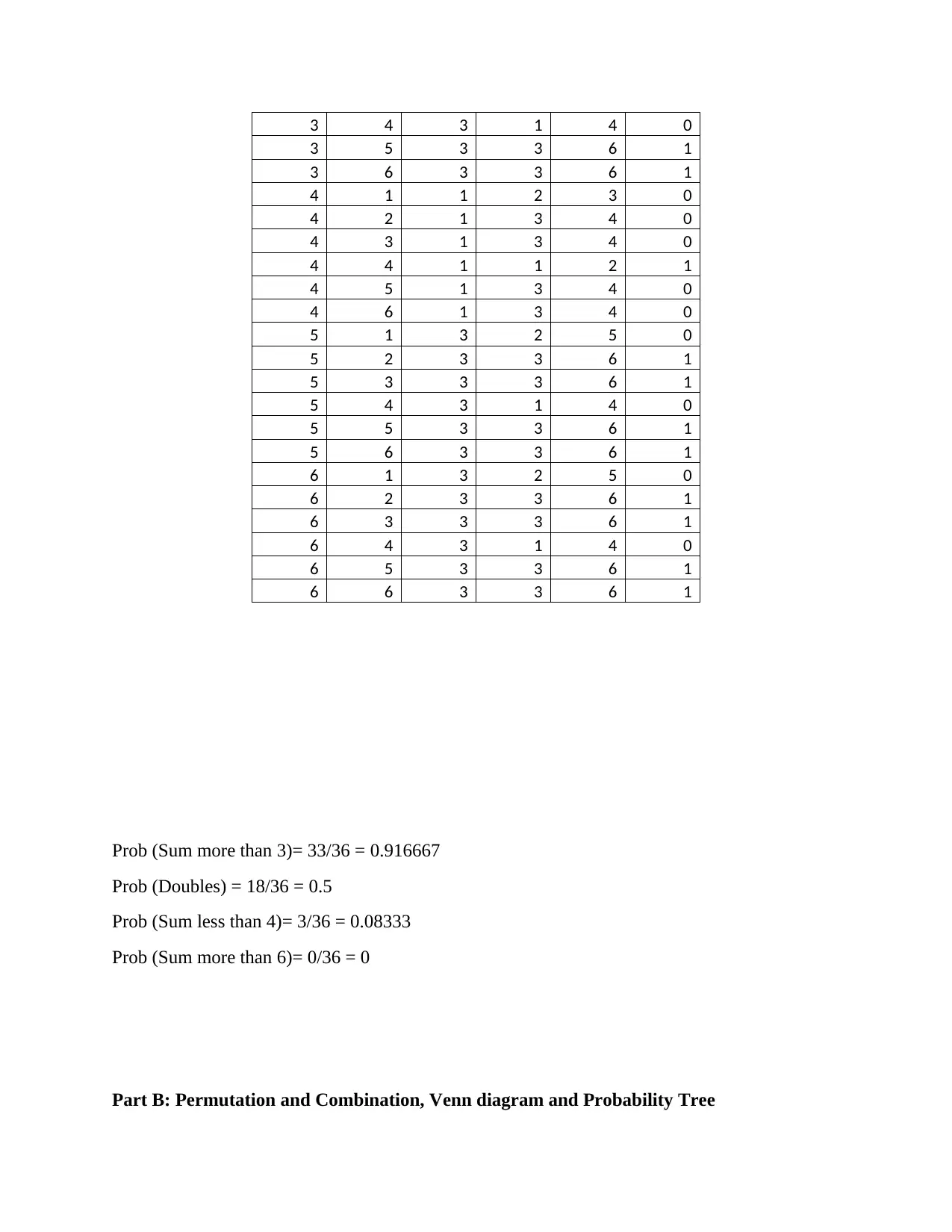
3 4 3 1 4 0
3 5 3 3 6 1
3 6 3 3 6 1
4 1 1 2 3 0
4 2 1 3 4 0
4 3 1 3 4 0
4 4 1 1 2 1
4 5 1 3 4 0
4 6 1 3 4 0
5 1 3 2 5 0
5 2 3 3 6 1
5 3 3 3 6 1
5 4 3 1 4 0
5 5 3 3 6 1
5 6 3 3 6 1
6 1 3 2 5 0
6 2 3 3 6 1
6 3 3 3 6 1
6 4 3 1 4 0
6 5 3 3 6 1
6 6 3 3 6 1
Prob (Sum more than 3)= 33/36 = 0.916667
Prob (Doubles) = 18/36 = 0.5
Prob (Sum less than 4)= 3/36 = 0.08333
Prob (Sum more than 6)= 0/36 = 0
Part B: Permutation and Combination, Venn diagram and Probability Tree

1.
We know that all possible arrangement of word having n letters out of which r1 is of
same kind, r2 is of same kind and r3 is of same kind is
= n! / (r1! r2! r3!)
So,
Probability of arrangement of word EXAGGERATE = 1 / (10 ! / (3! 2! 2!)) = 1 / 151200
When we have n things to be place then there are n! ways. Now position of one girl is
fixed so
Probability that girl will sit at the leftmost = 3! / 4! = 0.25
2. We obtain the required probability from the given table
a) P( Married) = 76 / 200
b) P(Female or single) = 138 / 200
c) P(Female and Widowed) = 11 / 200
d) P(male provided that single) = 38 /200
e) P (Male) = 100 / 200 = 0.5
f) Venn Diagram
3.
Male
Female
Single
Married
Windowed

Student
¼
3/4
Leader Followers
1/3 2/3 2/5 3/5
Cooperate Not cooperate Cooperate Not cooperate
Probability that student will not cooperate
= P(leader) * P(not cooperate) + P(follower) * P(not cooperate)
= ¼ * 2/3 + ¾ * 3/5 = 0.6167
Unit 2 Probability Distributions for Discrete variables and one variable
analysis
1
a)
l u x f fx cf
0 20 10 9 90 9
20 40 30 18 540 27
40 60 50 6 300 33
60 80 70 2 140 35
80 100 90 0 0 35
100 120 110 1 110 36
Total 36 1180

Mean= ∑ fx
∑ f =1180/ 36 = 32.7778
Median:
Here n=36 so 36/2=18 so
20-40 is median class
Median = l + (n/2 – cf) * w/ f
l is lower bound of median class
n is total frequency
cf is cumulative frequency of pre median class
f is frequency of median class
w is width of class
Here l=20, n=36, cf=9, f=18, w=20
Median = 20 + (36/2 – 9) * 20/ 18 = 20 + (18 – 9) * 20 / 18 = 20 + 10 = 30
Mode: the class which has highest frequency is modal class
20-40 is modal class.
Mode = l + (f1-f0)/((f1-f0)+(f1-f2))*w
l is lower bound of median class
f1 is frequency of modal class
f0 is frequency of premodal class
f2 is frequency of post modal class
w is width of class
Mode = 20 + (18 -9) / ((18 – 9) + (18 – 6)) * 20 = 28.57142857
b)

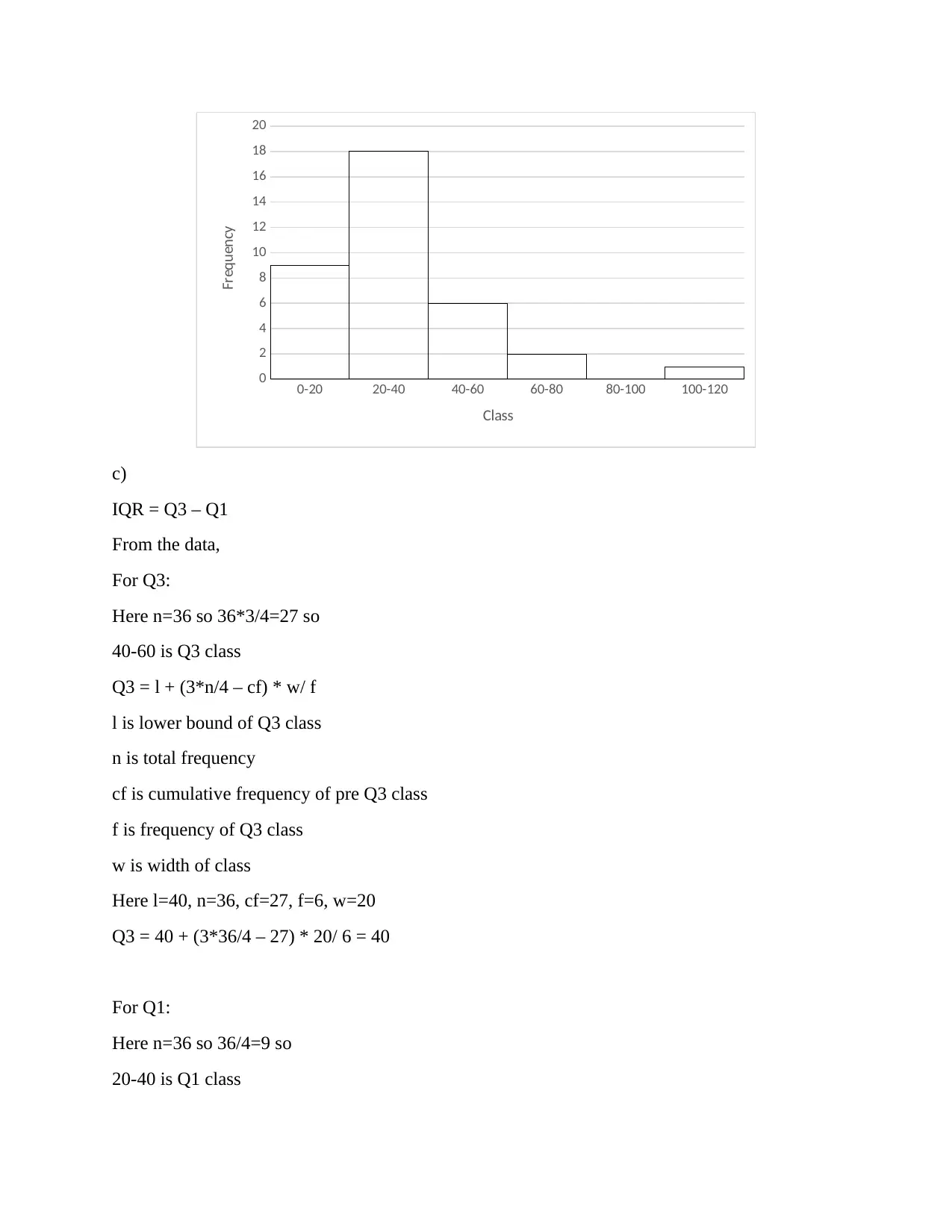
0-20 20-40 40-60 60-80 80-100 100-120
0
2
4
6
8
10
12
14
16
18
20
Class
Frequency
c)
IQR = Q3 – Q1
From the data,
For Q3:
Here n=36 so 36*3/4=27 so
40-60 is Q3 class
Q3 = l + (3*n/4 – cf) * w/ f
l is lower bound of Q3 class
n is total frequency
cf is cumulative frequency of pre Q3 class
f is frequency of Q3 class
w is width of class
Here l=40, n=36, cf=27, f=6, w=20
Q3 = 40 + (3*36/4 – 27) * 20/ 6 = 40
For Q1:
Here n=36 so 36/4=9 so
20-40 is Q1 class

Q1 = l + (n/4 – cf) * w/ f
l is lower bound of Q1 class
n is total frequency
cf is cumulative frequency of pre Q1 class
f is frequency of Q1 class
w is width of class
Here l=20, n=36, cf=9, f=18, w=20
Q3 = 20 + (36/4 – 9) * 20/18 = 20
So
Q3 = 40
Q1 = 20
IQR = 20
Box Whisker Plot

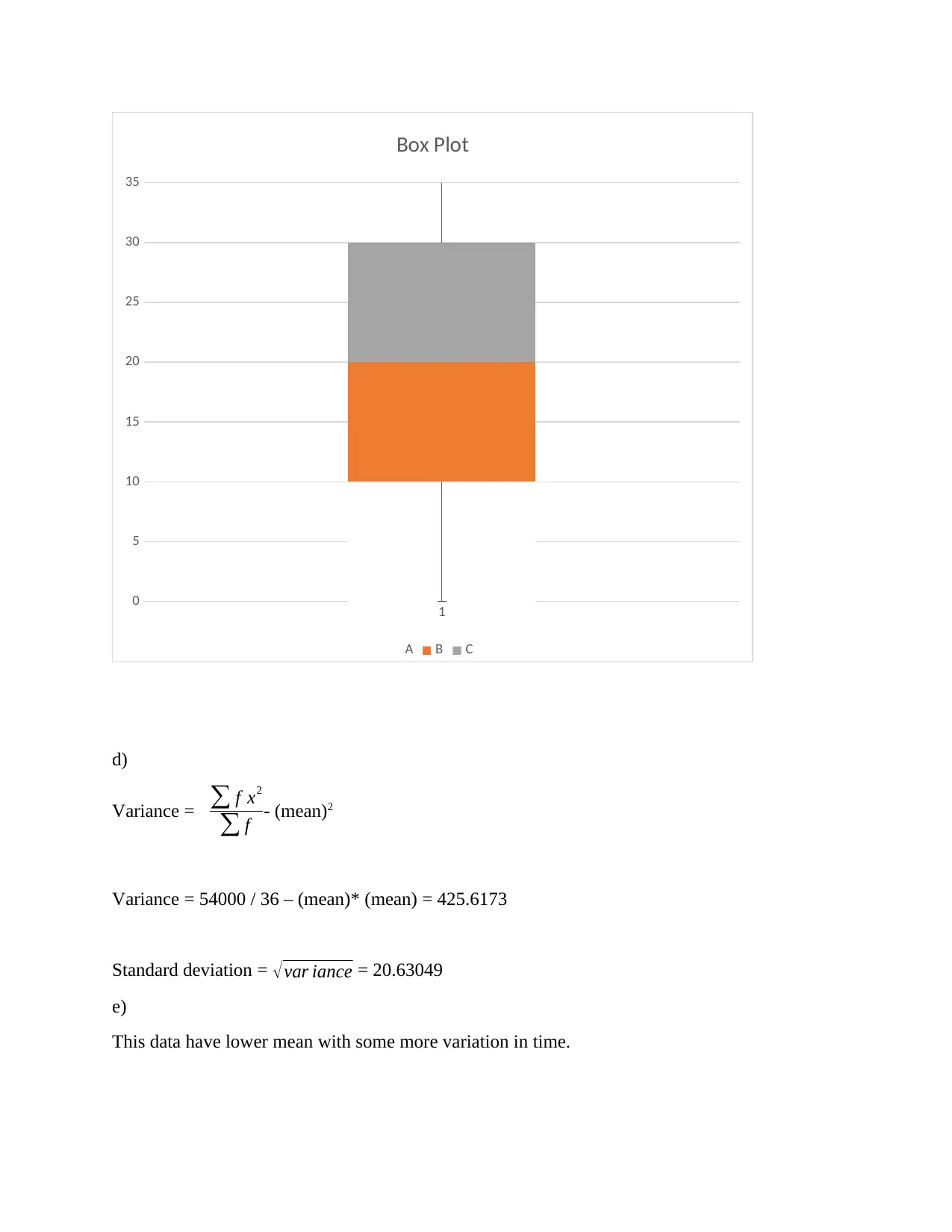
1
0
5
10
15
20
25
30
35
Box Plot
A B C
d)
Variance = ∑ f x2
∑ f - (mean)2
Variance = 54000 / 36 – (mean)* (mean) = 425.6173
Standard deviation = √var iance = 20.63049
e)
This data have lower mean with some more variation in time.

2.
We used MS Excel for the calculation.
a)
mean
31.9444
4
mode 12
Median 28.5
Q1 20.75
Q3 38.75
IQR 18
SD
21.6266
3
Var
467.711
1
b)
Mean, median and mode of grouped data is more than ungrouped data.
SD is minimum for grouped data than ungrouped data.
c)
74 and 118 are outliers in data
d)
mean
28.1764
7
mode 12
Median 27.5
Q1 20.25
Q3 38.75
IQR 18.5
SD
14.2626
2
Var 203.422

5
3.
Report:
From the given frequency distribution of time the cars spent on lot we observed that, the average
time spent by car on lot is 32.7778 days with standard deviation of 20.63 days. The minimum
time is 1 day while maximum day is 120 days.
From the histogram we can observed that data is positively skewed means most of the cars spent
less time on lot. First quartile and third quartile are equidistance from median. The upper part of
data is more skewed suggest that if car is more than 40 days on lot then the probability that it will
be there for longer time.

Unit 4: Probability Distribution for continuous variables and Two variable
Data Analysis
a)
b)

1.
We obtained the area/probability from normal distribution table and verified using MS Excel
function Norm.Dist
a)
Prob = 0.3907
b)

Prob = 0.282
c)
Prob = 0.0087
d)

Prob = 0.9332
e)
Prob = 0.1716
2.
We obtained the Z values from normal distribution table and verified using MS Excel function
Norm.inv

a)
Z= -0.95
b)
Z= 1.84
c)

Z= -0.002
d)
Z = -0.12
e)

Z = 3.012
PART B: Food Service Industry
a)
Mean 499.875
SD
1.57945
6
b)
Let X be the quantity of honey in gram
Given X follows normal distribution with mean 499.875 and sd 1.579456.
P(X<500) = P(Z < 0.079141179 ) = 0.531539835
c)
P(X < 500) <= 0.005

P(Z < (500 – mean) /sd ) <= 0.005
(500 – mean) / sd = -2.57
i.e. mean = -2.57 * sd + 500 = 495.94
Here we assume that standard deviation is constant.
d)
She can take the random sample and check it.
e)
P(X > 510 ) = P(Z > (510 - 495.94) / 1.579459) = P( Z > 9.534929255) = 0
f)
If any customers get honey less than 500 gram in 500 gram packet, company will give then
additional 50 gram honey sachet.
Unit 4: Statistical Analysis Graded Assignment
Q. No.1
Let X be the diameter of engine crankshafts for certain car model.
Given X follows Normal with mean 224 mm and sd 0.03 mm
P(X < 223.92 or X > 224.08) = P(X < 223.92) + P( X > 224.08)
= P( Z < -2.67) + P(Z > 2.67) = 0.00383 + 0.00383 = 0.00766
Q. No. 2
Using normal approximation:
Sample Size (n) Probability of Success (p)
Mea
n Variance Probability

600 0.4 240 144 P(X<22)= 4.73922E-74
200 0.7 140 42 P(X<160)= 0.998985884
75 0.6 45 18 P(X>50)= 0.119296415
250 0.2 50 40 P(X>48)= 0.624085183
1000 0.8 800 160 P(780<X<840)= 0.94229415
90 0.65 58.5 20.475 P(52<X<62)= 0.704952461
100 0.36 36 23.04 P(X=340)= 0
3000 0.52 1560 748.8 P(X=21650)= 0
Q. NO. 3
a) Management of driving school assume that each student at the starting stage knows
nothing (or same) about driving skill and obtained score is only due to the training. This
assumption is not reasonable as some of the students may know more about driving than
other.
b) We simply study the regression analysis which suggests that whether the students’ score
are related with instructional hours or not.
Regression Output:
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.046185
R Square 0.002133
Adjusted R Square -0.19744
Standard Error 17.43335
Observations 7
ANOVA
df SS MS F
Significan
ce F
Regression 1
3.24827
8
3.24827
8
0.01068
8 0.921678
Residual 5
1519.60
9
303.921
8
Total 6
1522.85
7
Coefficien
ts
Standar
d Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 79.79471
19.8663
8
4.01657
1
0.01015
5 28.72657
130.862
9
28.7265
7
130.862
9
instructional hours -0.13297
1.28620
3 -0.10338
0.92167
8 -3.43926
3.17331
9 -3.43926
3.17331
9

From the regression analysis it suggest that there is no significant relation between instructional
hours and students’ score. Each addition hour results in decline of the student score by 0.13297.
So, instructor is not effective.
c)
4 6 8 10 12 14 16 18 20 22
0
20
40
60
80
100
120
students’ score
From the above plot, we can see that 6th observation is unusual.
i,e, (20, 45)
d)
By removing the outlier, we again carry the regression analysis to check the effectiveness of
instructor
Regression Output:
SUMMARY OUTPUT
Regression Statistics

Multiple R 0.926188
R Square 0.857824
Adjusted R Square 0.82228
Standard Error 3.059401
Observations 6
ANOVA
df SS MS F
Significan
ce F
Regression 1
225.893
6
225.893
6 24.1341 0.007971
Residual 4
37.4397
3
9.35993
3
Total 5
263.333
3
Coefficien
ts
Standar
d Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 66.52455
3.64237
1
18.2640
8 5.29E-05 56.41171 76.6374
56.4117
1 76.6374
instructional hours 1.229911
0.25035
6
4.91264
7
0.00797
1 0.534811 1.92501
0.53481
1 1.92501
Now we observed that there is significant relation between instructional hours and students’
score. Each addition hour results in incline of the student score by 1.229911.
So, instructor is effective.
Q. NO. 4
a) The data is not reliable.
b) Data is collected from some part of America.
c) Data is collected for the in connection with king importance among the American.
Q. No. 5
a)

20 25 30 35 40 45 50 55 60 65
0
100
200
300
400
500
600
700
800
f
b)
Data is positively skewed.
c)
m
There may be younger than older in agricultural sector.
Younger may be more careless than older.
d)
Mean = 136817.5/3795 = 36.05
Average age of loss injury is 36.05.
Q. NO. 6
a)
We first convert into mean 0 and sd 1
Suppose X is old result with mean 55 and sd 13
So
Let Z = (X – 55)/ 13 have mean 0 and sd 1.

Now Y is new result with mean 70 and sd 10.
So,
Y= Z * 10 + 70
= (X-55)/13 *10 + 70
b)
if X= 80
then Y= 89.23
c)
if X=40
then Y= 58.46
Q. No.7
a)
Mean
43.9333
3
SD
10.8656
4
b) 6/15
Q. NO. 8
a)
Run the experiment in constant conditions.
b)
Check association between gender and study variables.

Q. NO. 9
a)
95% C. I.
p ± Z * SE(p)
p = Sum of all proportion / 33 = 0.16
Z= 1.96
SE(p) = √ p∗(1− p)/n
Where n=33
SE(p) = 0.063817923
95% C. I.
0.16 ± 1.96 * 0.063817923
(0.034916871, 0.285083129)
b) Letter
To,
Respected Mayor,

Town Name
Subject: Report about waste recycle in town with 5000 households
We analyzed the data of waste recycle data in 33 towns with 5000 households and found that
only 16% on an average waste recycle in town. We also observed that 95 % C. I. for waste recyle
is (3%, 28%). This analysis suggest that we should put the efforts to increase the amount of
waste recycle to keep clean the environment.
Thanking You.