Calculating Expectation and Variance

This document explains how to calculate the expectation and variance for a given set of data. It provides examples and step-by-step calculations for both expectation and variance. The document also includes information on probability calculations and hypothesis testing.

QUESTION 1a
Expected value is the mean. It measures the average unit of a given quantity. Expectation of
a variable x is computed using the following formula,
∑ x p (x) where the variable x is a discrete variable and the p(x) is the probability of the
variable x
Example
X 0 1 2 3 4
P (X = x) 0.16 0.53 0.2 0.08 0.03
Based on this example, we calculate the expectation of x as follows;
∑ x p (x)=x p ( X =0 ) +x p ( X =1 ) +x p ( X =2 )+ x p( X=3)+ x p( X=4)
= (0*0.16) + (1*0.53) + (2*0.2) + (3*0.08) + (4*0.03)
= 0 + 0.53 + 0.4 + 0.24 + 0.12
=1.29
QUESTION 1b (1)
SALES
UNIT (X)
NUMBER
OF DAYS P(X)
EXP
VALUE
MORE
THAN
LESS
THAN [X-E(X)] ^2 [X-[E(X)] ^2P(X)]
0 5 0.05 0 0.95 0.05 8.41 0.4205
1 10 0.1 0.1 0.85 0.15 3.61 0.361
2 25 0.25 0.5 0.6 0.4 0.81 0.2025
3 25 0.25 0.75 0.35 0.65 0.01 0.0025
4 20 0.2 0.8 0.15 0.85 1.21 0.242
5 15 0.15 0.75 0 1 4.41 0.6615
TOTAL 100 1 2.9
p(x≥2) =
0.6
p(x≤3)
=0.65 VARIANCE 1.89
STANDARD
DEVIATION 1.374772708

QUESTION 1(b) 2.
The average daily sales
E(X) = X1P1 + X2P2 + X3P3 + X4P4 + X5P5 + X6P6
= 0*0 + 1*0.1 + 2* 0.5 + 3* 0.75 + 4* 0.8 + 5* 0.75
= 2.9
QUESTION 1(b) 3
P (x ≥ 2) = 1 – p (x ≤ 2)
= 1 – (p(x=0) + p (x =1) + p (x =2))
=1 – (0.05 + 0.1 + 0.25)
=1- 0.4
=0.6
QUESTION 1(b) 4
p (x ≤ 3)
=p(x=0) + p(x=1) + p(x=2) + p(x=3)
=0.05 + 0.1 + 0.25 + 0.25
= 0.65
QUESTION 1(b) 5
The variance is 1.89
Sum([X-[E(X)]2P(X)])
=8.41*0.05 + 3.61*0.1 + 0.81*0.25 + 0.01*0.25 + 1.21*0.2 + 4.41*0.15
=0.4205 + 0.361 + 0.2025 + 0.0025 + 0.242 + 0.66
= 1.89

QUESTION 1(b)6
Standard deviation is 1.374772708
= sqrt (8.41*0.05 + 3.61*0.1 + 0.81*0.25 + 0.01*0.25 + 1.21*0.2 + 4.41*0.15)
=sqrt (0.4205 + 0.361 + 0.2025 + 0.0025 + 0.242 + 0.66)
=sqrt (1.89)
=1.374772708
QUESTION 1(c)1
Probability of machine W is 3200/8000 = 0.15
Probability of rework on w is 600/4000 =0.4
The probability being produced by machine w and should be reworked is now computed as
follows
Probability of machine W * Probability of rework on W
= 0.15*0.4 = 0.06
QUESTION 1(c)2
The probability that the grade is satisfactory is 3200/4000 = 0.4
The probability of not being satisfactory is therefore 1-0.4 = 0.6
Probability that machine Z is picked is 1600/8000 = 0.8
Therefore, the probability that the grade was produced by a part Z and was not satisfactory
is calculated as follows;
Probability that machine Z is picked * The probability of not being satisfactory
=0.8*0.6 = 0.48

QUESTION 1(c)3
Probability of being scrapped is 150/3000 = 0.05
Probability of machine y is 150/500 = 0.3
Probability that the grade was produced by machine y and should be scrapped is calculated
as follows;
=Probability of machine y * Probability of being scrapped
= 0.03*0.05 = 0.015
QUESTION 1(c)4
The probability that grades needs to be reworked
= (0.8*0.4) + (0.8*0.1) + (0.8*0.3) + (0.8*0.2)
= 0.32+ 0.01 + 0.24 + 0.16
=0.73
QUESTION 1(c)5
P (scrapped/machine w) = p (scrapped and machine w)/p (machine w)
= 0.05*0.4/0.05
= 0.4
QUESTION 1(d)1
P (X > 4250) = 1 – P(X≤4250)
P (X≤4250) = X−μ
standard deviation
= 4250−4000
500 = 250/500
= 0.5
P (Z≤ 0.5) = 0.6915
= P (X > 4250) = 1 – 0.6915
= 0.3085

QUESTION 1(d)2
P (X < 3600) = P(X≤3600)
P (X≤3600) = 3600−4000
500
= - 0.8
P (Z≤ -0.8) = 0.2119
= 0.2119
QUESTION 1(d)3
P (X < 4500) = P(X≤4500)
P (X≤3600) = 4500−4000
500
= 1
P (Z≤ 1) = 0.8413
= 0.8413
QUESTION 3 (a) 1
The sample = 64 observations
Mean time = 20 hrs.
Standard deviation = 5 hrs.
Therefore, to calculate the upper and lower confidence interval (TÉLLEZ ARNOLDO,
2015), we proceed as follows,
To allow for degrees of freedom, we subtract 1 from the sample observation
= 64-1
At 95% level of confidence, (1-0.95)/2 = 0.025
Checking 0.025 in the t table for 9 degree of freedom, we get 2.262
Therefore

= standard deviation/ (sqrt (sample observation))
= σ
√ sample observation
= 5
√64 = 0.625
For the lower confidence interval
Mean (time) – 0.625
= 20 -0.625
= 19.375
For the Upper confidence interval
Mean (time) – 0.625
= 20 + 0.625
= 20.625
QUESTION 3 (a) 2
For a sample of 9 observations,
At 95% level of confidence, (1-0.95)/2 = 0.025
σ
√ sample observation
= 5
√9
= 1.666667
For the lower confidence interval
Mean time – 1.666667

= 20 -1.666667
= 18.33333
For the Upper confidence interval
Mean time – 1.666667
= 20 + 1.666667
= 21.66667
QUESTION 3 (b) 1
According to (Christos Lionis, 2010), We formulate a hypothesis as follows
H0: μ ≤ m (There no age discrimination)
H1: μ ≥ m (There is age discrimination)
QUESTION 3 (b) 2
To calculate the critical value, (Fantz, 2010) emphasized on the steps to follow procedurally
in order to obtain the critical value. Therefore, we proceed as follows
We first compute the formula;
Z =
μ−m
σ
√ n
Z =
45−42
10.8
√ 49
=
3
10.8
7
= 3
1.542857143
= 1.9444

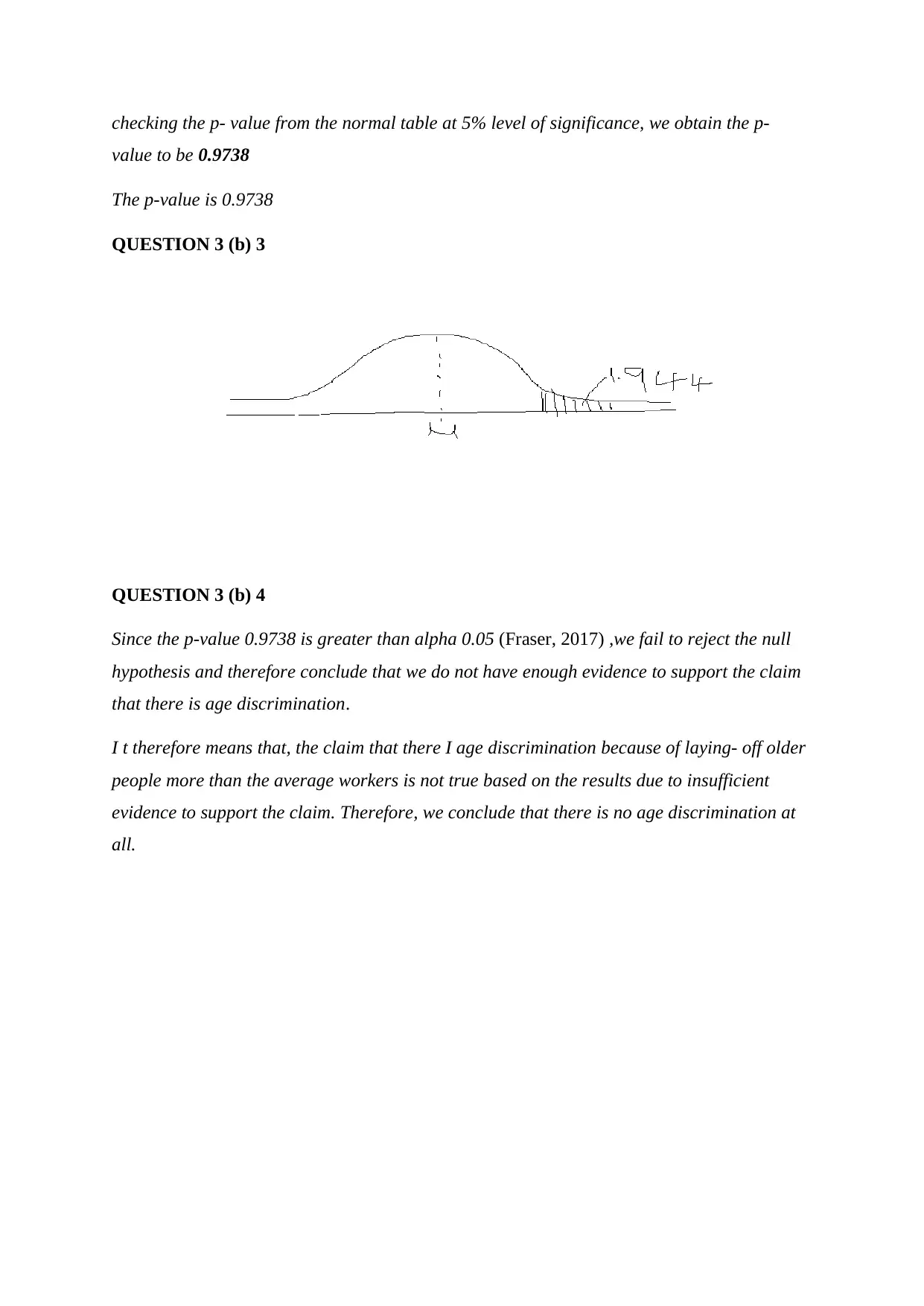
checking the p- value from the normal table at 5% level of significance, we obtain the p-
value to be 0.9738
The p-value is 0.9738
QUESTION 3 (b) 3
QUESTION 3 (b) 4
Since the p-value 0.9738 is greater than alpha 0.05 (Fraser, 2017) ,we fail to reject the null
hypothesis and therefore conclude that we do not have enough evidence to support the claim
that there is age discrimination.
I t therefore means that, the claim that there I age discrimination because of laying- off older
people more than the average workers is not true based on the results due to insufficient
evidence to support the claim. Therefore, we conclude that there is no age discrimination at
all.

References
Christos Lionis, D. A. (2010). Bio-psychosocial determinants of cardiovascular disease in a rural
population on Crete, Greece: formulating a hypothesis and designing the SPILI-III study.
Journal of hypothesis testing, 3(1), 2-16.
Fantz, C. (2010). Strategies for Evaluating Critical Value Limits: Opportunities for Saving Time and
Money Without Compromising Care. Critical Values, 3(1), 36-58.
Fraser, D. (2017). p -Values: The Insight to Modern Statistical Inference. Annual Review of Statistics
and Its Application, 4(1), 83-92.
Mukherjea, S. (2014). Conditional expected durations of play given the ultimate outcome for a
correlated walk. Statistics and probability letters, 104-118.
TÉLLEZ ARNOLDO, G. C.-V. (2015). Effect size, confidence intervals and statistical power in
psychological research. Psychology in Russia: State of the art, 8(3), 28-39.