Regression Analysis and Hypothesis Testing in Statistics

This document covers regression analysis, scatter plot, correlation coefficient, coefficient of determination, hypothesis testing and more in statistics with solved examples. It also includes sample regression lines, t-statistics, p-values and significance levels. The document is useful for students studying statistics and related courses in colleges and universities.

STATISTICS
[Type the document subtitle]
Student Name
[Pick the date]

Question 1
(a) Scatter plot
Dependent variable: Team winning %
Independent variable: Team batting average
0.245 0.25 0.255 0.26 0.265 0.27 0.275 0.28 0.285
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
f(x) = 2.98984526112185 x − 0.284358317214699
R² = 0.241477813185592
Scatter Plot
Team Batting Average
Team Winning %
It is apparent from the positive slope of the best fit line that there is a positive correlation
between the given variables. However, considered that the points have significant deviation from
the best fit line, it is apparent that the correlation is weak to moderate only and not strong (Flick,
2015).
(b) Correlation coefficient is calculated though CORREL () function of excel and is shown
below.

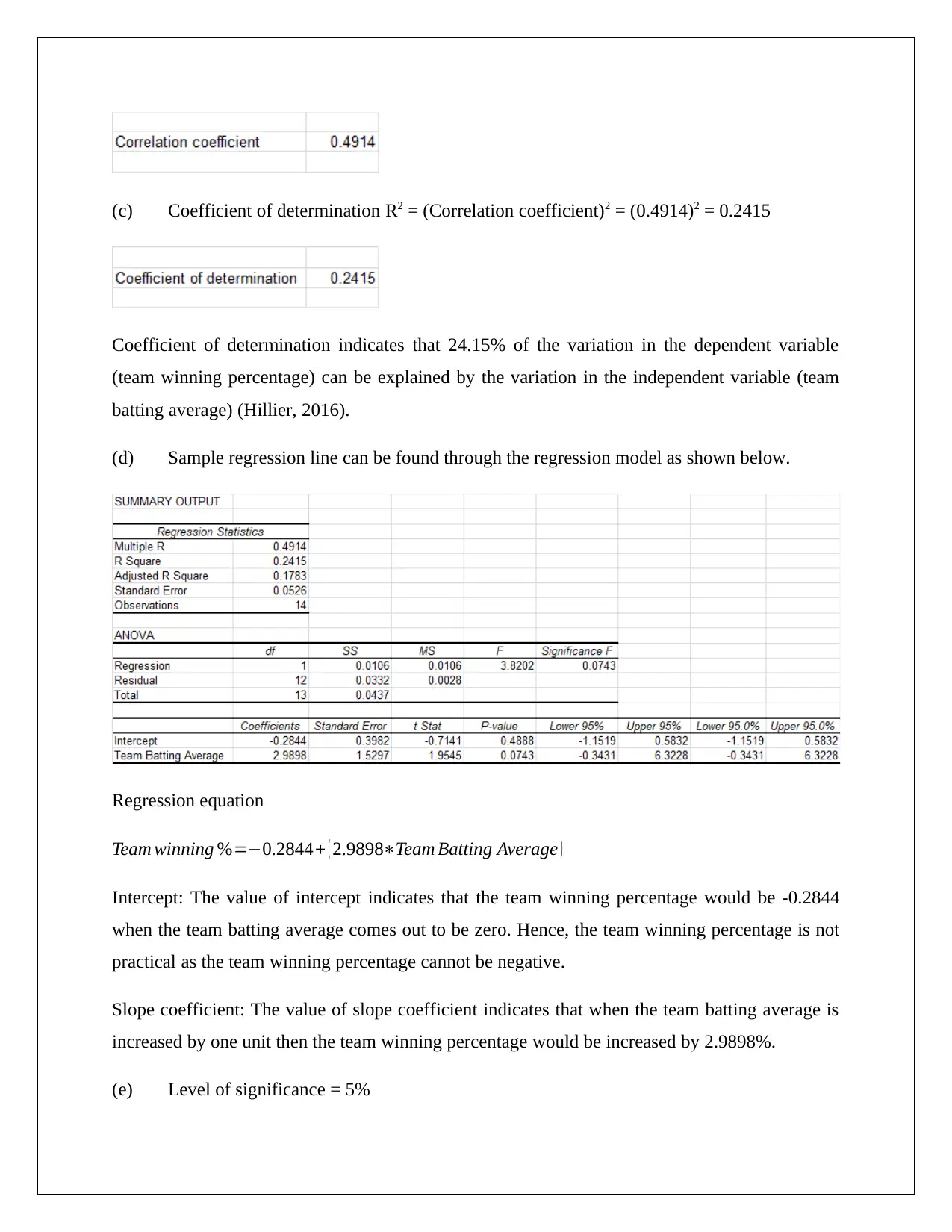
(c) Coefficient of determination R2 = (Correlation coefficient)2 = (0.4914)2 = 0.2415
Coefficient of determination indicates that 24.15% of the variation in the dependent variable
(team winning percentage) can be explained by the variation in the independent variable (team
batting average) (Hillier, 2016).
(d) Sample regression line can be found through the regression model as shown below.
Regression equation
Team winning %=−0.2844+ ( 2.9898∗Team Batting Average )
Intercept: The value of intercept indicates that the team winning percentage would be -0.2844
when the team batting average comes out to be zero. Hence, the team winning percentage is not
practical as the team winning percentage cannot be negative.
Slope coefficient: The value of slope coefficient indicates that when the team batting average is
increased by one unit then the team winning percentage would be increased by 2.9898%.
(e) Level of significance = 5%

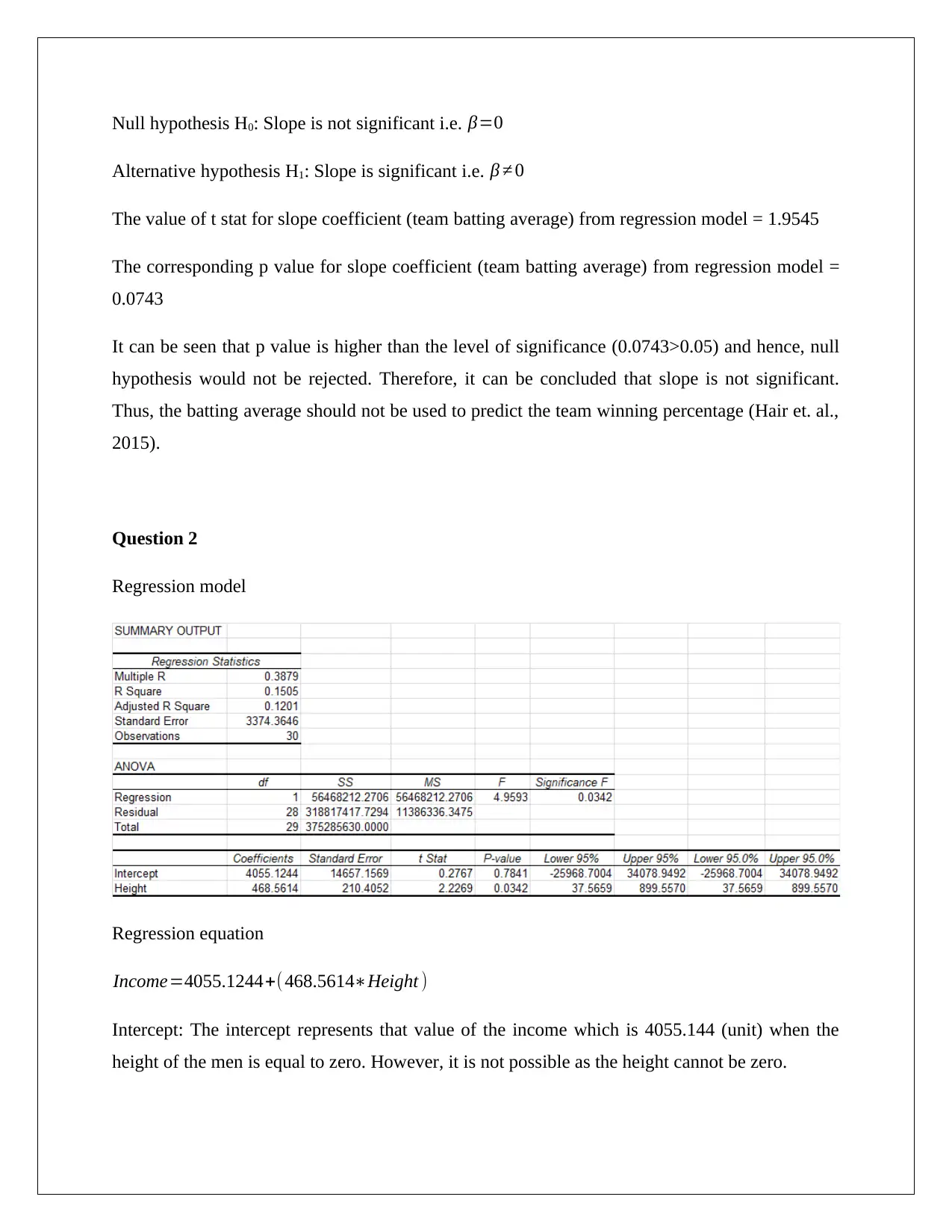
Null hypothesis H0: Slope is not significant i.e. β=0
Alternative hypothesis H1: Slope is significant i.e. β ≠ 0
The value of t stat for slope coefficient (team batting average) from regression model = 1.9545
The corresponding p value for slope coefficient (team batting average) from regression model =
0.0743
It can be seen that p value is higher than the level of significance (0.0743>0.05) and hence, null
hypothesis would not be rejected. Therefore, it can be concluded that slope is not significant.
Thus, the batting average should not be used to predict the team winning percentage (Hair et. al.,
2015).
Question 2
Regression model
Regression equation
Income=4055.1244+( 468.5614∗Height )
Intercept: The intercept represents that value of the income which is 4055.144 (unit) when the
height of the men is equal to zero. However, it is not possible as the height cannot be zero.

Slope coefficient: The value of slope coefficient represents that when the height of a men is
increased by one unit then the income of the men would be increased by $468.56
The t value of slope coefficient (height) comes out to be 2.2269 and the corresponding p value
comes out to be 0.0342. Assuming 5% of level of significance, it can be seen that p value is
lower than the level of significance and hence, the slope is significant (Eriksson & Kovalainen,
2015). Therefore, the conclusion can be drawn that taller graduates earn more than the shorter
graduates.
Question 3
Regression equation
Y =125.1 + 0.46 X1 +25.7 X2
The corresponding t stat is 10.2, 6.9 and 1.7 respectively.
(i) X2 is a dummy variable and the coefficient 25.7 implies that sales generated in the spring or
summer quarter would be higher by $ 25,700 in comparison to the corresponding sales
generated in the fall or winter quarter (Flick, 2015).
(ii) The t statistic pertaining to seasonal effects variables X2 is 1.7 which with degrees of
freedom as 39 would lead to a p value being greater than 0.05. Considering a significance
level of 5%, it would be appropriate to conclude that the slope coefficient of X2 can be
assumed as zero and hence the seasonal effect is not apparent (Hair et. al., 2015).
Question 4
(a) Multiple regression model
Dependent variable: Salary
Independent variable: Education, Experience, Sex

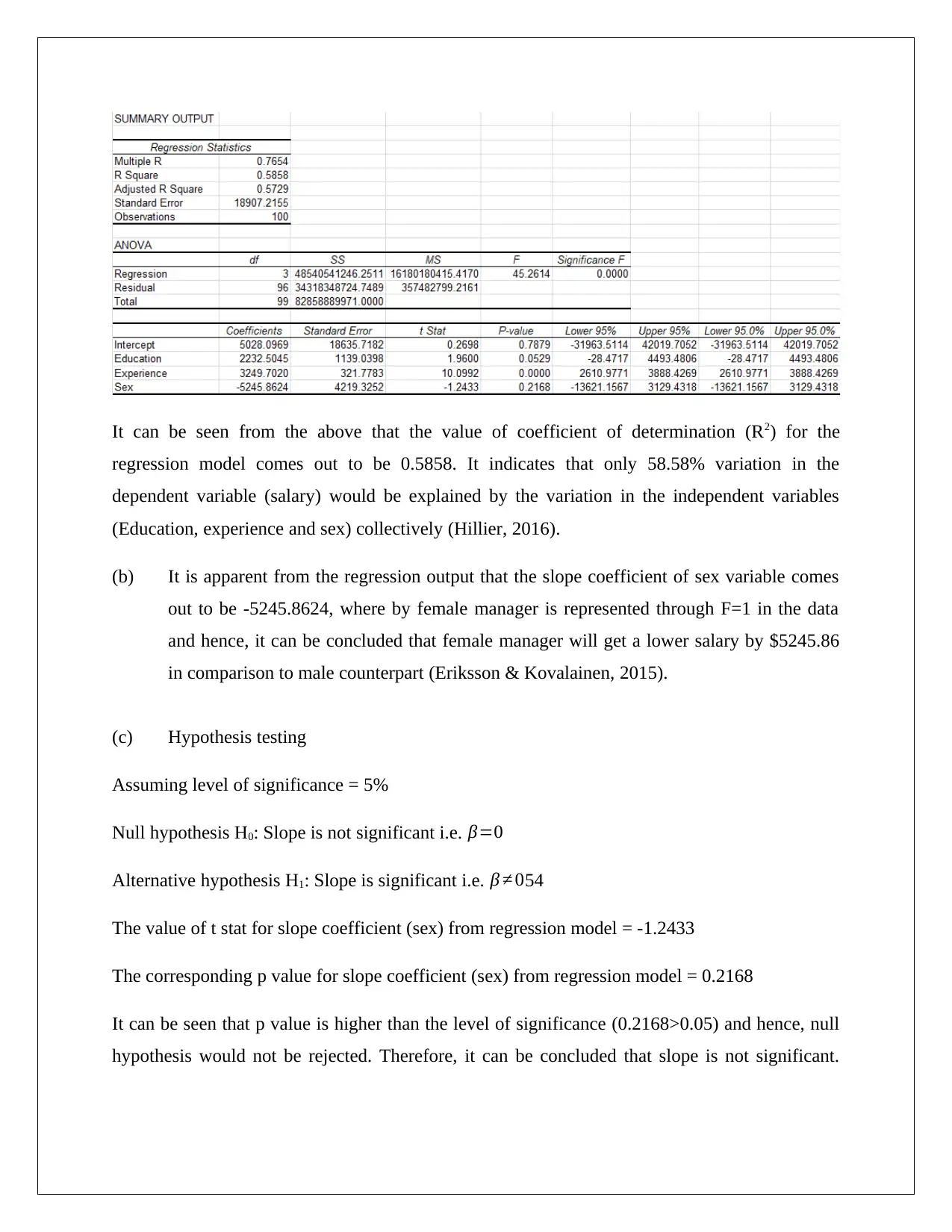
It can be seen from the above that the value of coefficient of determination (R2) for the
regression model comes out to be 0.5858. It indicates that only 58.58% variation in the
dependent variable (salary) would be explained by the variation in the independent variables
(Education, experience and sex) collectively (Hillier, 2016).
(b) It is apparent from the regression output that the slope coefficient of sex variable comes
out to be -5245.8624, where by female manager is represented through F=1 in the data
and hence, it can be concluded that female manager will get a lower salary by $5245.86
in comparison to male counterpart (Eriksson & Kovalainen, 2015).
(c) Hypothesis testing
Assuming level of significance = 5%
Null hypothesis H0: Slope is not significant i.e. β=0
Alternative hypothesis H1: Slope is significant i.e. β ≠ 054
The value of t stat for slope coefficient (sex) from regression model = -1.2433
The corresponding p value for slope coefficient (sex) from regression model = 0.2168
It can be seen that p value is higher than the level of significance (0.2168>0.05) and hence, null
hypothesis would not be rejected. Therefore, it can be concluded that slope is not significant.

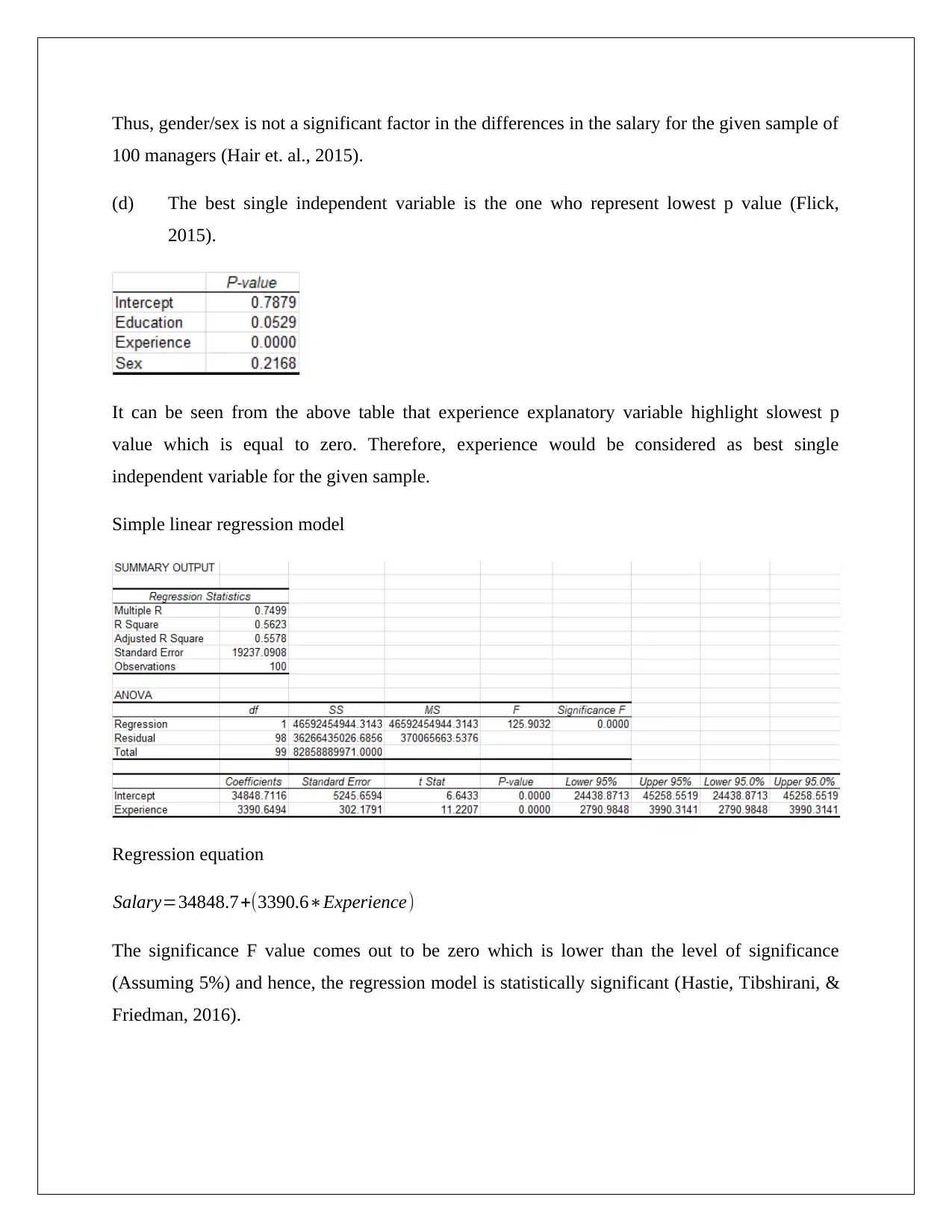
Thus, gender/sex is not a significant factor in the differences in the salary for the given sample of
100 managers (Hair et. al., 2015).
(d) The best single independent variable is the one who represent lowest p value (Flick,
2015).
It can be seen from the above table that experience explanatory variable highlight slowest p
value which is equal to zero. Therefore, experience would be considered as best single
independent variable for the given sample.
Simple linear regression model
Regression equation
Salary=34848.7+(3390.6∗Experience)
The significance F value comes out to be zero which is lower than the level of significance
(Assuming 5%) and hence, the regression model is statistically significant (Hastie, Tibshirani, &
Friedman, 2016).

References
Eriksson, P. & Kovalainen, A. (2015) Quantitative methods in business research (3rd ed.).
London: Sage Publications.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project (4th ed.). New York: Sage Publications.
Hair, J. F., Wolfinbarger, M., Money, A. H., Samouel, P., & Page, M. J. (2015) Essentials of
business research methods (2nd ed.). New York: Routledge.
Hastie, T., Tibshirani, R. & Friedman, J. (2016) The Elements of Statistical Learning (4th
ed.). New York: Springer Publications.
Hillier, F. (2016) Introduction to Operations Research. (6th ed.). New York: McGraw Hill
Publications