Rotary Inverted Pendulum Report
VerifiedAdded on 2023/04/20
|21
|3366
|113
AI Summary
This report provides an in-depth analysis of the rotary inverted pendulum system. It covers topics such as system modeling, controller design, linearization, state feedback design, and simulation. The report also discusses the stability of the system and provides real-life examples of inverted pendulums. The aim of the experiment, system model equations, and the design of the controller are explained in detail. The report concludes with a discussion on the simulation results and future works.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

ROTARY INVERTED
PENDULUM
REPORT
2019
STUDENT NAME
INSTITUTIONAL AFFILIATION
1/1/2019
PENDULUM
REPORT
2019
STUDENT NAME
INSTITUTIONAL AFFILIATION
1/1/2019
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

ABSTRACT
1
1

Table of Contents
INTRODUCTION.......................................................................................................................................1
SYSTEM MODEL......................................................................................................................................1
CONTROLLER DESIGN...........................................................................................................................1
Linearization...........................................................................................................................................1
State Feedback Design............................................................................................................................1
Zero-Pole Map Design............................................................................................................................1
SIMULATION & DISCUSSION................................................................................................................1
Model Simulation: Free & Forced Response...........................................................................................1
Closed Loop Simulation: With/Without Disturbance...............................................................................1
EXPERIMENT & DISCUSSION...............................................................................................................1
CONCLUSION & FUTURE WORKS........................................................................................................2
REFERENCES............................................................................................................................................2
APPENDIX.................................................................................................................................................2
2
INTRODUCTION.......................................................................................................................................1
SYSTEM MODEL......................................................................................................................................1
CONTROLLER DESIGN...........................................................................................................................1
Linearization...........................................................................................................................................1
State Feedback Design............................................................................................................................1
Zero-Pole Map Design............................................................................................................................1
SIMULATION & DISCUSSION................................................................................................................1
Model Simulation: Free & Forced Response...........................................................................................1
Closed Loop Simulation: With/Without Disturbance...............................................................................1
EXPERIMENT & DISCUSSION...............................................................................................................1
CONCLUSION & FUTURE WORKS........................................................................................................2
REFERENCES............................................................................................................................................2
APPENDIX.................................................................................................................................................2
2

INTRODUCTION
The current industrial age requires a high level of automation which ensures that the
repetitive tasks are carried out using machines and the systems have controller which guarantee
the intended system output is obtained. Control systems are used in real-life applications
especially in the industrial setting. The inverted pendulum is a critical evaluation in the design
and structure of a control system where the system is made up of a cart that seeks to stabilize an
inverted pendulum or balancing rod on it. The cart is powered by a motor and it moves while
ensuring that the rod is in the upright vertical position. The background of the inverted pendulum
dates to the balance the broomstick game from ancient days.
The control theory mimics the human body reaction to external stimuli as demonstrated
in the block diagram below,
The stability of the inverted pendulum as the cart is propelled by the motor change based
on the angle of inversion of the inverted pendulum held on the cart. The control theory is
implemented in the design and development of the controller suitable for the inverted pendulum
3
The current industrial age requires a high level of automation which ensures that the
repetitive tasks are carried out using machines and the systems have controller which guarantee
the intended system output is obtained. Control systems are used in real-life applications
especially in the industrial setting. The inverted pendulum is a critical evaluation in the design
and structure of a control system where the system is made up of a cart that seeks to stabilize an
inverted pendulum or balancing rod on it. The cart is powered by a motor and it moves while
ensuring that the rod is in the upright vertical position. The background of the inverted pendulum
dates to the balance the broomstick game from ancient days.
The control theory mimics the human body reaction to external stimuli as demonstrated
in the block diagram below,
The stability of the inverted pendulum as the cart is propelled by the motor change based
on the angle of inversion of the inverted pendulum held on the cart. The control theory is
implemented in the design and development of the controller suitable for the inverted pendulum
3
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

defining the tuning methods for varied components of the system. Some of the common
controllers are the PID controllers, fuzzy logic controller, and Proportional or proportional
derivative controllers. The system is modeled using the system variables and a proper analysis of
the free body diagram of the cart and pendulum using the control effects. The sum of forces
around the rotational points is evaluated and the dynamics of the pendulum are evaluated.
The real life applications are non-linear by default and the controller is implemented on
linear systems. It is crucial to linearize the inverted pendulum by linearizing the transfer function
based around the equilibrium of the non-linear system based on the upright vertical position for
balancing purposes. The problem is identified in the implementation of a real life inverted
pendulum. Consider a pendulum relative to the vertical axis, in its upright position, the system is
said to be unstable. A slight external force on the system may cause the pendulum in its upright
position to fall off hence the system is considered unstable. A controller and feedback loop are
designed to meet the condition. Therefore, the main aim of designing a controller is to ensure
that the pendulum is kept in an upright position.
Some of the real life examples of inverted pendulums include the Segway personal
transporter, a self-balancing vehicle, and the Rocket MAXUS 1 in its launching position at the
Esrange Space Center in Kiruna. The inverted pendulum system consists of a cart linked to a
motor whose torque propels the motion such that it is able to balance the pendulum. The
propulsion requires a controller that maintains the balance on the pendulum. The mechanical
model of the system has the cart, the pendulum, the track, and the motion mechanism. In the
design, it is important to note that the cart motion is limited to a single degree of freedom; the
pendulum motion is limited to two degrees of freedom. There is a cause of friction between the
cart and a pendulum.
4
controllers are the PID controllers, fuzzy logic controller, and Proportional or proportional
derivative controllers. The system is modeled using the system variables and a proper analysis of
the free body diagram of the cart and pendulum using the control effects. The sum of forces
around the rotational points is evaluated and the dynamics of the pendulum are evaluated.
The real life applications are non-linear by default and the controller is implemented on
linear systems. It is crucial to linearize the inverted pendulum by linearizing the transfer function
based around the equilibrium of the non-linear system based on the upright vertical position for
balancing purposes. The problem is identified in the implementation of a real life inverted
pendulum. Consider a pendulum relative to the vertical axis, in its upright position, the system is
said to be unstable. A slight external force on the system may cause the pendulum in its upright
position to fall off hence the system is considered unstable. A controller and feedback loop are
designed to meet the condition. Therefore, the main aim of designing a controller is to ensure
that the pendulum is kept in an upright position.
Some of the real life examples of inverted pendulums include the Segway personal
transporter, a self-balancing vehicle, and the Rocket MAXUS 1 in its launching position at the
Esrange Space Center in Kiruna. The inverted pendulum system consists of a cart linked to a
motor whose torque propels the motion such that it is able to balance the pendulum. The
propulsion requires a controller that maintains the balance on the pendulum. The mechanical
model of the system has the cart, the pendulum, the track, and the motion mechanism. In the
design, it is important to note that the cart motion is limited to a single degree of freedom; the
pendulum motion is limited to two degrees of freedom. There is a cause of friction between the
cart and a pendulum.
4

The implementation considers the type of motor used to propel the cart to move along the
track. The DC motor, stepper motor, or the servo motor may be implemented based on torque
generated and the speed. The lab experiment used a separate power supply to power the
LABVIEW setup. The input of the system is the force that is applied to the cart through the
motor. The horizontal link is coupled such that it links directly or by connecting to a gearing of
the motor shaft and the rotary motion.
AIMS OF THE EXPERIMENT
(I) To determine the system modeling of the rotary inverted pendulum in terms of
motion based on the Euler and Lagrangian methods.
(II) To determine the stability levels of the open loop and closed loop with and without
disturbances from the surrounding.
(III) To develop a simulation of the inverted pendulum on MATLAB Simulink to observe
the system analysis and the operation and system responses to ensure balance and
stability is achieved.
5
track. The DC motor, stepper motor, or the servo motor may be implemented based on torque
generated and the speed. The lab experiment used a separate power supply to power the
LABVIEW setup. The input of the system is the force that is applied to the cart through the
motor. The horizontal link is coupled such that it links directly or by connecting to a gearing of
the motor shaft and the rotary motion.
AIMS OF THE EXPERIMENT
(I) To determine the system modeling of the rotary inverted pendulum in terms of
motion based on the Euler and Lagrangian methods.
(II) To determine the stability levels of the open loop and closed loop with and without
disturbances from the surrounding.
(III) To develop a simulation of the inverted pendulum on MATLAB Simulink to observe
the system analysis and the operation and system responses to ensure balance and
stability is achieved.
5

SYSTEM MODEL
To determine the equation of motion, the linear motion and circular motion are considered such
that,
F=ma= m d2 x
d t2
τ =Iα=I d2 θ
d t2
τ total=I d2 θ
d t2
To determine the torque based on gravity and the oscillating pivot, the forced response is given
as,
τ grav=rF sin θ
τ grav=mgl sin θ
y ( t ) =A cos ωt
a= d2 y ( t )
d t2 =−ω2 A cos ( ωt )
F=ma=m d2 y ( t )
d t2 =−mω2 A cos ωt
τ pivot=r F sin θ
τ pivot=−ml ω2 A cos ωt sin θ
To obtain the comprehensive equation of motion,
6
To determine the equation of motion, the linear motion and circular motion are considered such
that,
F=ma= m d2 x
d t2
τ =Iα=I d2 θ
d t2
τ total=I d2 θ
d t2
To determine the torque based on gravity and the oscillating pivot, the forced response is given
as,
τ grav=rF sin θ
τ grav=mgl sin θ
y ( t ) =A cos ωt
a= d2 y ( t )
d t2 =−ω2 A cos ( ωt )
F=ma=m d2 y ( t )
d t2 =−mω2 A cos ωt
τ pivot=r F sin θ
τ pivot=−ml ω2 A cos ωt sin θ
To obtain the comprehensive equation of motion,
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

τ grav +τ pivot =τtotal=I d2 θ
d t2 =m l2 d2 θ
d t2
ml2 d2 θ
d t2 =mgl sinθ−mg ω2 A cos ωt sin θ
Therefore,
d2 θ
d t2 − [ g
l − ω2 A
l cos ωt ]sin θ=0
Using the Euler equation to find motion,
M ¨x +b ˙x +N=F
N=m ¨x +ml ¨θ cos θ−ml ¨θ2 sin θ
( M +m ) ¨x +b ˙x +ml ¨θ cos θ−ml ¨θ2 sin θ=F
( I +ml2 ) ¨θ+mgl sin θ=−ml ¨x cos θ
( I +ml2 ) ¨φ−mglφ=ml ¨x
( M +m ) ¨x +b ˙x−ml ¨φ=u
( I +ml2 ) s2 Φ (s)−mgl Φ (s)=ml s2 X ( s )
( M +m ) s2 X ( s ) +bsX ( s)−ml s2 Φ ( s )=U ( s)
( M +m ) s2
[ I +ml2
ml − g
s2 ]Φ ( s ) +bs [ I+ ml2
ml − g
s2 ]Φ ( s )−ml s2 Φ ( s )=U (s)
The equation of motion formulates the transfer function below,
7
d t2 =m l2 d2 θ
d t2
ml2 d2 θ
d t2 =mgl sinθ−mg ω2 A cos ωt sin θ
Therefore,
d2 θ
d t2 − [ g
l − ω2 A
l cos ωt ]sin θ=0
Using the Euler equation to find motion,
M ¨x +b ˙x +N=F
N=m ¨x +ml ¨θ cos θ−ml ¨θ2 sin θ
( M +m ) ¨x +b ˙x +ml ¨θ cos θ−ml ¨θ2 sin θ=F
( I +ml2 ) ¨θ+mgl sin θ=−ml ¨x cos θ
( I +ml2 ) ¨φ−mglφ=ml ¨x
( M +m ) ¨x +b ˙x−ml ¨φ=u
( I +ml2 ) s2 Φ (s)−mgl Φ (s)=ml s2 X ( s )
( M +m ) s2 X ( s ) +bsX ( s)−ml s2 Φ ( s )=U ( s)
( M +m ) s2
[ I +ml2
ml − g
s2 ]Φ ( s ) +bs [ I+ ml2
ml − g
s2 ]Φ ( s )−ml s2 Φ ( s )=U (s)
The equation of motion formulates the transfer function below,
7

Φ ( s )
U ( s ) =
ml
q s2
s4+ ( b ( I +ml2 )
q ) s3− ( ( M+ m ) mgl
q )s2−bmgl
q s
q= [ ( M +m ) ( I + ml2 )− ( ml ) 2 ]
To determine the kinetic and potential energies of the system bodies,
T 0= 1
2 m0 ˙θ0 P0 =0
The Lagrangian function L provides the difference between the system’s potential and kinetic
energy. The value is given as,
L=T −P
L= ( T 0 +T 1 )− ( P0 + P1 )
T 1=1
2 m1 [ ( ˙θ0 + L
2 ˙θ1 cos θ1 )
2
+ ( L
2 ˙θ1 sinθ1 )
2
] + 1
2 I ˙θ1
T 1=1
2 m1 ˙θ0
2 +m1
L
2 ˙θ0 ˙θ1 cos θ1 + 1
2 [m1
L
2 + I ] ˙θ1
2
P1=m1 g L
2 cos θ1
The Lagrangian function is given as,
L= 1
2 ( m0 +m1 ) ˙θ0
2 +m1
L
2 ˙θ0 ˙θ1 cos θ1 + 1
2 [ m1
L
2 + I ] ˙θ1
2 +m1 g L
2 cos θ1
8
U ( s ) =
ml
q s2
s4+ ( b ( I +ml2 )
q ) s3− ( ( M+ m ) mgl
q )s2−bmgl
q s
q= [ ( M +m ) ( I + ml2 )− ( ml ) 2 ]
To determine the kinetic and potential energies of the system bodies,
T 0= 1
2 m0 ˙θ0 P0 =0
The Lagrangian function L provides the difference between the system’s potential and kinetic
energy. The value is given as,
L=T −P
L= ( T 0 +T 1 )− ( P0 + P1 )
T 1=1
2 m1 [ ( ˙θ0 + L
2 ˙θ1 cos θ1 )
2
+ ( L
2 ˙θ1 sinθ1 )
2
] + 1
2 I ˙θ1
T 1=1
2 m1 ˙θ0
2 +m1
L
2 ˙θ0 ˙θ1 cos θ1 + 1
2 [m1
L
2 + I ] ˙θ1
2
P1=m1 g L
2 cos θ1
The Lagrangian function is given as,
L= 1
2 ( m0 +m1 ) ˙θ0
2 +m1
L
2 ˙θ0 ˙θ1 cos θ1 + 1
2 [ m1
L
2 + I ] ˙θ1
2 +m1 g L
2 cos θ1
8

d
dt ( ∂ L
∂ ˙θ )− ( ∂ L
∂θ )=P
CONTROLLER DESIGN
Linearization
The real life rotary inverted pendulum is a non-linear system in nature and for proper analysis, it
is necessary to linearize the system. The angle of the pendulum remains small and there is ample
control required to have a balance on the system. The linearization process reduces the moment
of inertia, I, in the Lagrangian and Euler equations of the system model to zero to simplify the
system dynamics.
State Feedback Design
A feedback network is needed to ensure that the system response is obtained as
anticipated. The system uses sensors at the feedback loop. The sensor obtains the output
information accurately and reflects the state of the system. The system variables are analyzed
and determined as the angle, angular velocity, the cart’s displacement, and the cart’s velocity.
There are four measurable parameters needed to determine the control needed in stabilizing a
system. The system modeling determines the proper design of the controller. The section on the
system model discusses the system dynamics model for the non-linear inverted pendulum
system. There is an assumption that the system is frictionless and hence it can be discussed as a
disturbance in the simulation section.
The state space model is obtained to enable easier simulation of the system in MATLAB
software. The state space vector is obtained as,
9
dt ( ∂ L
∂ ˙θ )− ( ∂ L
∂θ )=P
CONTROLLER DESIGN
Linearization
The real life rotary inverted pendulum is a non-linear system in nature and for proper analysis, it
is necessary to linearize the system. The angle of the pendulum remains small and there is ample
control required to have a balance on the system. The linearization process reduces the moment
of inertia, I, in the Lagrangian and Euler equations of the system model to zero to simplify the
system dynamics.
State Feedback Design
A feedback network is needed to ensure that the system response is obtained as
anticipated. The system uses sensors at the feedback loop. The sensor obtains the output
information accurately and reflects the state of the system. The system variables are analyzed
and determined as the angle, angular velocity, the cart’s displacement, and the cart’s velocity.
There are four measurable parameters needed to determine the control needed in stabilizing a
system. The system modeling determines the proper design of the controller. The section on the
system model discusses the system dynamics model for the non-linear inverted pendulum
system. There is an assumption that the system is frictionless and hence it can be discussed as a
disturbance in the simulation section.
The state space model is obtained to enable easier simulation of the system in MATLAB
software. The state space vector is obtained as,
9
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

[ x
˙x
ϕ
˙ϕ ]
The system’s performance metrics are based on the angle of the pendulum and the
displacement of the cart. The state space system are defined as,
x= Ax+ Bu u+ Bw w
z=Cz x +Dzu u+ Dzw w
When the state-space representation is given,
[ ˙x
¨x
˙ϕ
¨ϕ ]=
[ 0 1 0 0
0 − ( I +ml2 ) b
I ( M +m ) + Mml2
m2 g l2
I ( M+ m ) + Mml2 0
0 0 0 1
0 −mlb
I ( M +m ) + Mml2
mgl ( M + m )
I ( M+ m ) + Mml2 0 ] [ x
˙x
ϕ
˙ϕ ] +
[ 0
I +m l2
I ( M+ m ) +Mm l2
0
ml
I ( M+ m ) +Mm l2 ] u
y= [1 0 0 0
0 0 1 0 ] [ x
˙x
ϕ
˙ϕ ]+[0
0 ]u
10
˙x
ϕ
˙ϕ ]
The system’s performance metrics are based on the angle of the pendulum and the
displacement of the cart. The state space system are defined as,
x= Ax+ Bu u+ Bw w
z=Cz x +Dzu u+ Dzw w
When the state-space representation is given,
[ ˙x
¨x
˙ϕ
¨ϕ ]=
[ 0 1 0 0
0 − ( I +ml2 ) b
I ( M +m ) + Mml2
m2 g l2
I ( M+ m ) + Mml2 0
0 0 0 1
0 −mlb
I ( M +m ) + Mml2
mgl ( M + m )
I ( M+ m ) + Mml2 0 ] [ x
˙x
ϕ
˙ϕ ] +
[ 0
I +m l2
I ( M+ m ) +Mm l2
0
ml
I ( M+ m ) +Mm l2 ] u
y= [1 0 0 0
0 0 1 0 ] [ x
˙x
ϕ
˙ϕ ]+[0
0 ]u
10

The state space is represented using the block diagram below to illustrate the open loop
system and matrices as,
Zero-Pole Map Design
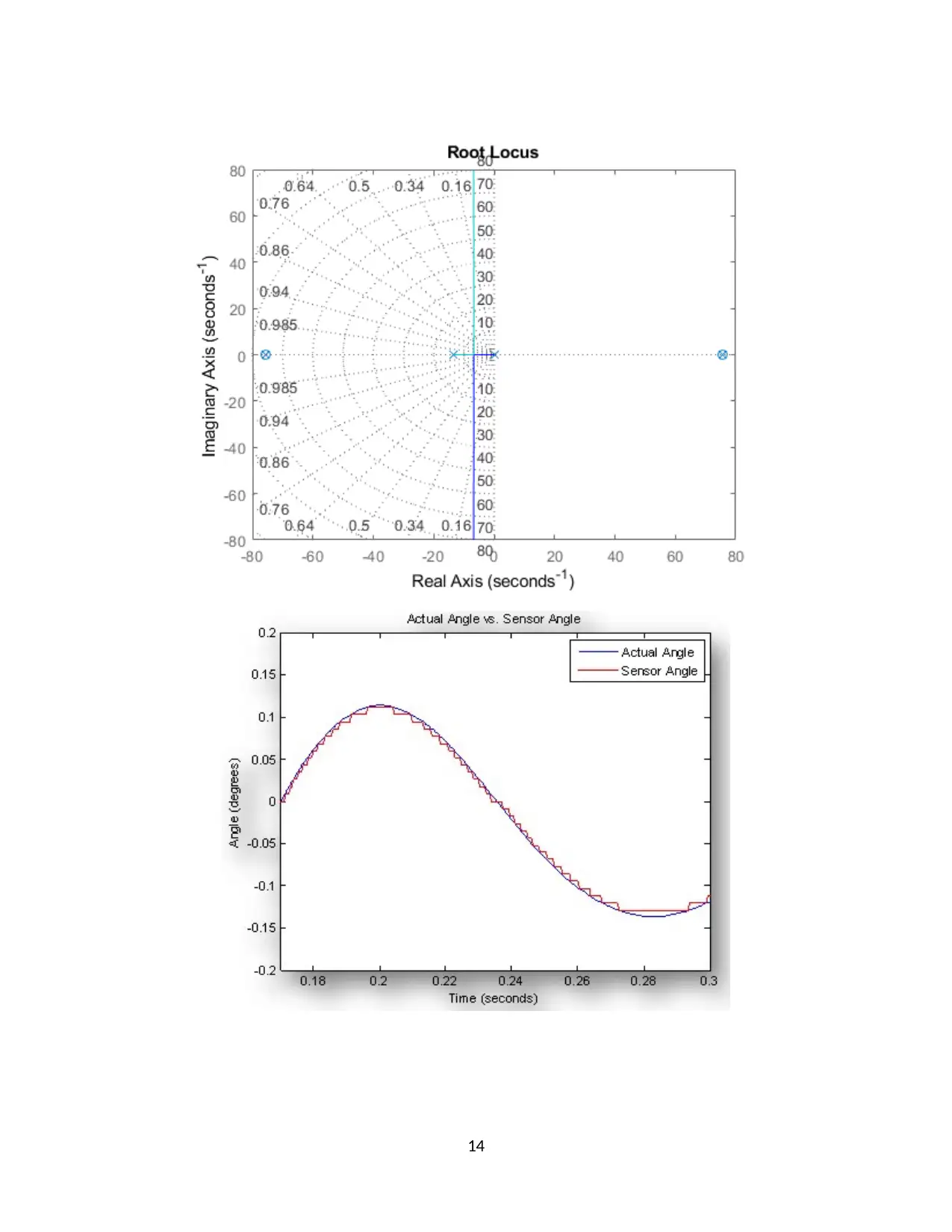
It is required that the poles in a system lie on the left hand side for stability and their real
parts are always negative. The controller is implemented with the aim of stabilizing a system by
placing poles to ensure that they lie on the left hand side of the root locus output.
The transfer function’s characteristic equation is analyzed to determine the system
response attributes especially when the function is not complex. The system poles are used to
11
system and matrices as,
Zero-Pole Map Design
It is required that the poles in a system lie on the left hand side for stability and their real
parts are always negative. The controller is implemented with the aim of stabilizing a system by
placing poles to ensure that they lie on the left hand side of the root locus output.
The transfer function’s characteristic equation is analyzed to determine the system
response attributes especially when the function is not complex. The system poles are used to
11

determine the system stability based on the side they lie on the s plane. The poles are obtained as
the roots of the characteristic equation and can be determined using the rlocus function on the
MATLAB software. The method goes further to place poles so that the unstable system can be
made stable by adjusting the pole location. The poles and zeros are, therefore, considered to be
properties that make up the transfer function and in turn they determine the differential equation
of motion for the rotary inverted pendulum. The linearization process of the rotary inverted
pendulum is quite important as it converts the non-linear system to a linear system which can be
analyzed. The poles must have negative real parts for the system to be stable.
SIMULATION & DISCUSSION
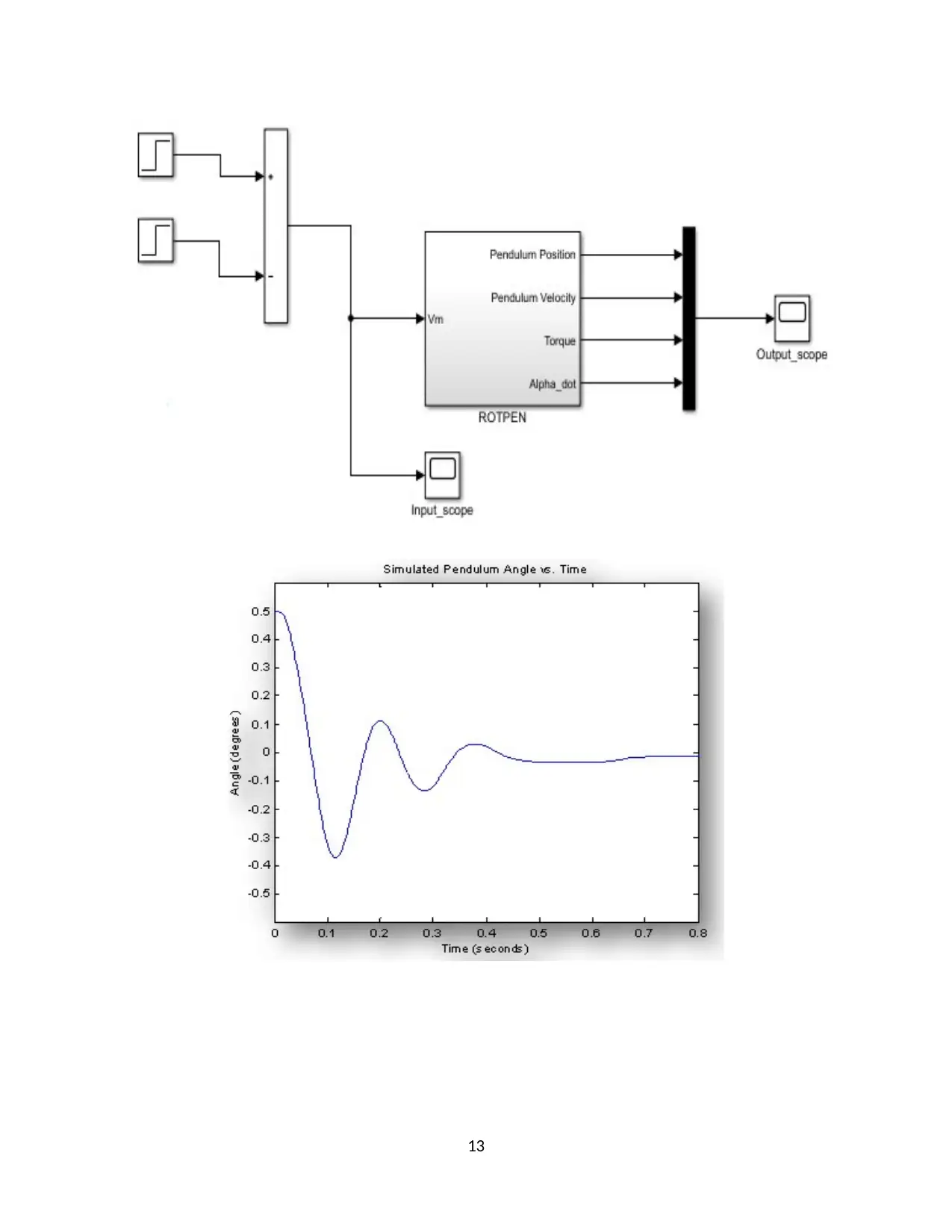
Model Simulation: Free & Forced Response
The system depends on a MATLAB script that highlights all the values of the system
parameters which the Simulink obtains from the workspace once it is run. The nonlinear
equation of motion is rearranged so as to obtain an acceleration form of the equation, with
respect to the Newtonian law of motion.
12
the roots of the characteristic equation and can be determined using the rlocus function on the
MATLAB software. The method goes further to place poles so that the unstable system can be
made stable by adjusting the pole location. The poles and zeros are, therefore, considered to be
properties that make up the transfer function and in turn they determine the differential equation
of motion for the rotary inverted pendulum. The linearization process of the rotary inverted
pendulum is quite important as it converts the non-linear system to a linear system which can be
analyzed. The poles must have negative real parts for the system to be stable.
SIMULATION & DISCUSSION
Model Simulation: Free & Forced Response
The system depends on a MATLAB script that highlights all the values of the system
parameters which the Simulink obtains from the workspace once it is run. The nonlinear
equation of motion is rearranged so as to obtain an acceleration form of the equation, with
respect to the Newtonian law of motion.
12
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
13
14
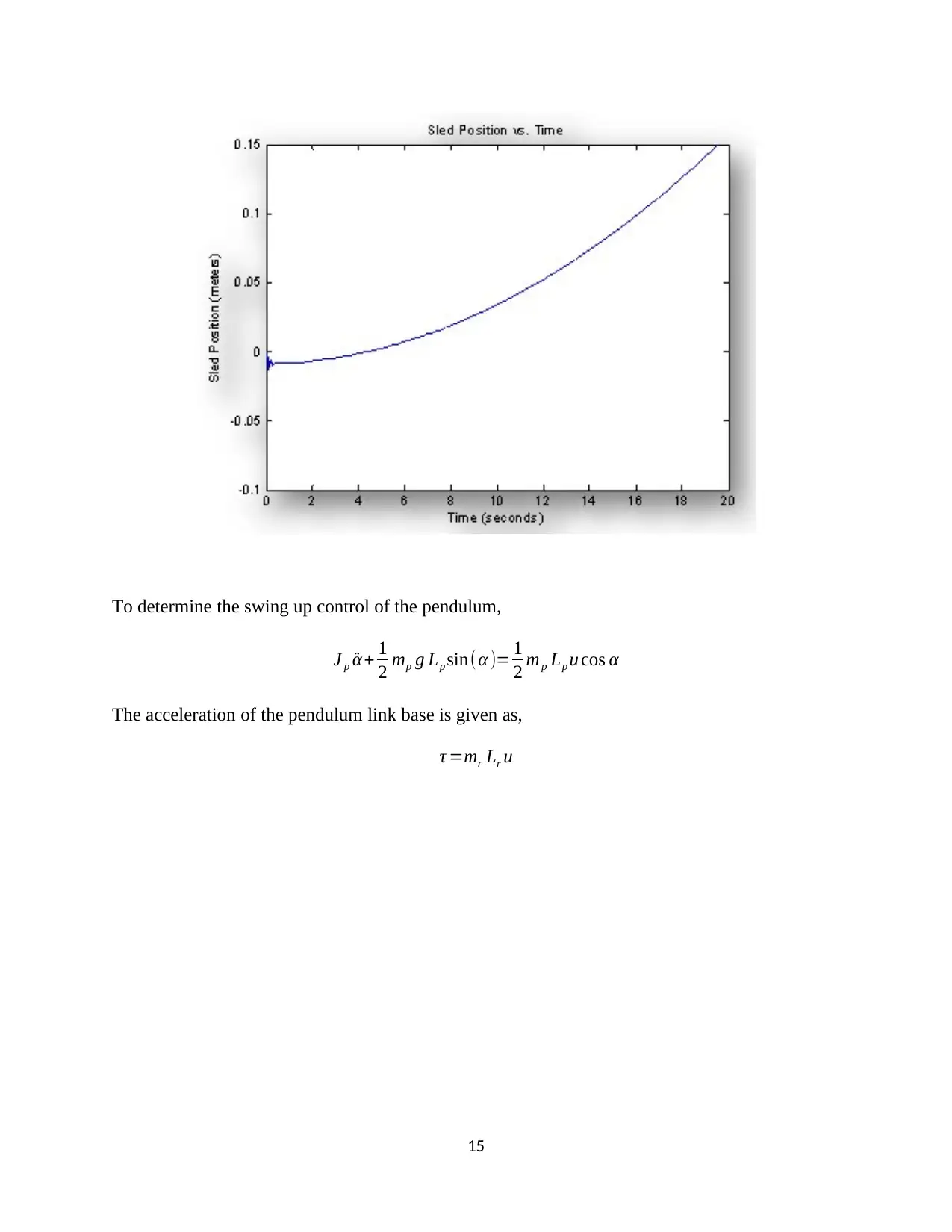
To determine the swing up control of the pendulum,
J p ¨α+ 1
2 mp g Lp sin(α )= 1
2 mp Lp u cos α
The acceleration of the pendulum link base is given as,
τ =mr Lr u
15
J p ¨α+ 1
2 mp g Lp sin(α )= 1
2 mp Lp u cos α
The acceleration of the pendulum link base is given as,
τ =mr Lr u
15
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
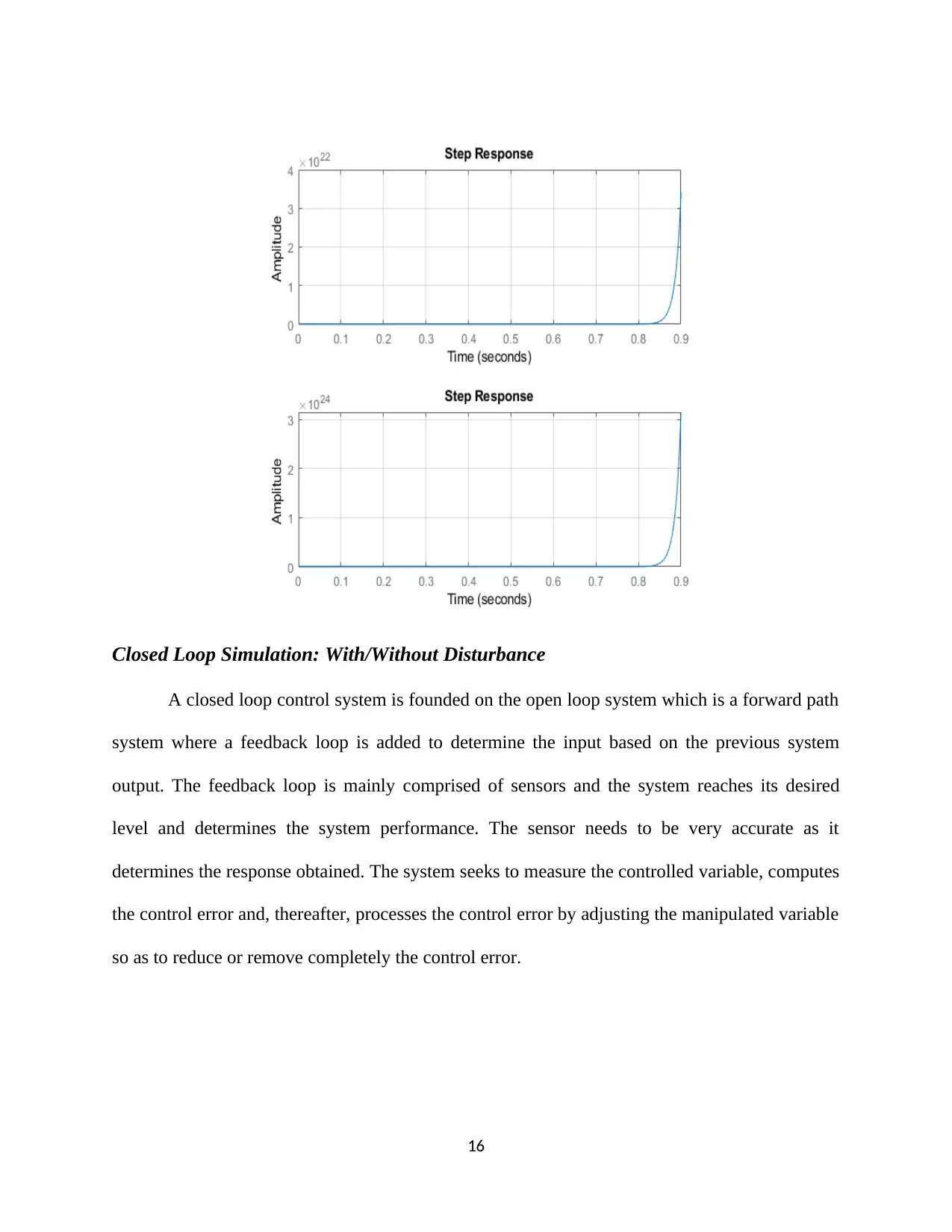
Closed Loop Simulation: With/Without Disturbance
A closed loop control system is founded on the open loop system which is a forward path
system where a feedback loop is added to determine the input based on the previous system
output. The feedback loop is mainly comprised of sensors and the system reaches its desired
level and determines the system performance. The sensor needs to be very accurate as it
determines the response obtained. The system seeks to measure the controlled variable, computes
the control error and, thereafter, processes the control error by adjusting the manipulated variable
so as to reduce or remove completely the control error.
16
A closed loop control system is founded on the open loop system which is a forward path
system where a feedback loop is added to determine the input based on the previous system
output. The feedback loop is mainly comprised of sensors and the system reaches its desired
level and determines the system performance. The sensor needs to be very accurate as it
determines the response obtained. The system seeks to measure the controlled variable, computes
the control error and, thereafter, processes the control error by adjusting the manipulated variable
so as to reduce or remove completely the control error.
16

When the state feedback controller is implemented in the closed loop simulation with
disturbance considered as the Additive white Gaussian noise,
EXPERIMENT & DISCUSSION
The classical controller is designed for either a SISO or MIMO system through the
manipulation of the system variables. There are virtual measurements required for the car t
displacement to be related to the angle of the system. Some of the common design tools that
analyze the impact of a system controller are the bode plots, root locus, Nichols or the Nyquist
plots. They provide a very simple implementation and are more suited for SISO compared to the
MIMO systems. When modeling, it is important to monitor the system variables in the most
17
disturbance considered as the Additive white Gaussian noise,
EXPERIMENT & DISCUSSION
The classical controller is designed for either a SISO or MIMO system through the
manipulation of the system variables. There are virtual measurements required for the car t
displacement to be related to the angle of the system. Some of the common design tools that
analyze the impact of a system controller are the bode plots, root locus, Nichols or the Nyquist
plots. They provide a very simple implementation and are more suited for SISO compared to the
MIMO systems. When modeling, it is important to monitor the system variables in the most
17

elementary number of relations to avoid long iterative processes when analyzing all variables at a
single instance.
There are a number of cost factors taken into consideration such as the linear quadratic
regulator or the implementation of the kalman filter using the observer and a pre-compensator for
further analysis. Adding a controller and a feedback loop transforms an open loop system to a
closed loop system. The feedback loop seeks to check if the output obtained is equal to the
desired output. The robustness of the control system was analyzed using the transfer functions of
the linearized system to determine the state space model for implementation on MATLAB
Simulink. The output demonstrates the poles falling on the left hand side so that the system is
considered to be stable and robust.
There is a slight variation in the real system which makes the accurate simulation
predictions challenging. The rotary inverted pendulum has been expressed as a mathematical
model which is based on the simulated hypothetical situations as well as the synthesized
controllers. The system obtains the nominal model, calibration model, and the model error. The
model is based on the mathematical equations intended to capture the effects of the certain
system variables on certain other system variables. The system captures the kinetic and potential
models with equations of motion using the Euler and Lagrangian models.
The nonlinear system based on the rotary inverted pendulum is linearized so that it is user
defined for the operating point. The model takes in several inputs and the system response is
captured using the scope and some information is saved in mat files. In summary, the experiment
had issues maintaining the angle for system stability and there was need for a good controller to
manage the system balancing.
18
single instance.
There are a number of cost factors taken into consideration such as the linear quadratic
regulator or the implementation of the kalman filter using the observer and a pre-compensator for
further analysis. Adding a controller and a feedback loop transforms an open loop system to a
closed loop system. The feedback loop seeks to check if the output obtained is equal to the
desired output. The robustness of the control system was analyzed using the transfer functions of
the linearized system to determine the state space model for implementation on MATLAB
Simulink. The output demonstrates the poles falling on the left hand side so that the system is
considered to be stable and robust.
There is a slight variation in the real system which makes the accurate simulation
predictions challenging. The rotary inverted pendulum has been expressed as a mathematical
model which is based on the simulated hypothetical situations as well as the synthesized
controllers. The system obtains the nominal model, calibration model, and the model error. The
model is based on the mathematical equations intended to capture the effects of the certain
system variables on certain other system variables. The system captures the kinetic and potential
models with equations of motion using the Euler and Lagrangian models.
The nonlinear system based on the rotary inverted pendulum is linearized so that it is user
defined for the operating point. The model takes in several inputs and the system response is
captured using the scope and some information is saved in mat files. In summary, the experiment
had issues maintaining the angle for system stability and there was need for a good controller to
manage the system balancing.
18
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

CONCLUSION & FUTURE WORKS
The aims of the experiment were met as the system was linearized from its non-linear
system state. The system was modeled using the Euler- Lagrangian equations of motion. The
system was able to define the linear state space representation of the system using the separation
technique of the transfer functions. The state feedback controller was model to manage the
balancing and stability of the pendulum in its upright position. The experiment performed a
matlab simulation of the system in open loop and closed loop state. The simulation responses
were obtained and are included in the report as well as properly reviewed in the discussion
sections. The system was determined using the model and the disturbances included in the
system were overcome using the feedback loop and the designed controller.
REFERENCES
[1]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
[2]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control of
a Multi degree of Freedom Flexible Joint Manipulator”. 2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
[3]. Md. Akhtaruzzaman and A. A. Shafie”Control of a Rotary Inverted Pendulum Using
Various Methods, Comparative Assessment and Result Analysis” International
Conference on Mechatronics and AutomationAugust 4-7, 2010, Xi'an, China
[4]. Swing-Up and Stabilization of Rotary Inverted Pendulum, Mertl, Jaroslav Sobota, Milo·s
Schlegel, Pavel Balda,
19
The aims of the experiment were met as the system was linearized from its non-linear
system state. The system was modeled using the Euler- Lagrangian equations of motion. The
system was able to define the linear state space representation of the system using the separation
technique of the transfer functions. The state feedback controller was model to manage the
balancing and stability of the pendulum in its upright position. The experiment performed a
matlab simulation of the system in open loop and closed loop state. The simulation responses
were obtained and are included in the report as well as properly reviewed in the discussion
sections. The system was determined using the model and the disturbances included in the
system were overcome using the feedback loop and the designed controller.
REFERENCES
[1]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
[2]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control of
a Multi degree of Freedom Flexible Joint Manipulator”. 2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
[3]. Md. Akhtaruzzaman and A. A. Shafie”Control of a Rotary Inverted Pendulum Using
Various Methods, Comparative Assessment and Result Analysis” International
Conference on Mechatronics and AutomationAugust 4-7, 2010, Xi'an, China
[4]. Swing-Up and Stabilization of Rotary Inverted Pendulum, Mertl, Jaroslav Sobota, Milo·s
Schlegel, Pavel Balda,
19

[5]. Purtojo, R. Akmeliawati and Wahyudi, “Two-parameter Compensator Design for Point-
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[6]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-ofFreedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
[7]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
[8]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control
of a Multi degree of Freedom Flexible Joint Manipulator”,2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
[9]. Masanori Yukitomo, Takashi Shigemasa, Yasushi Baba, Fumia Kojima, “A Two
Degrees of Freedom PID Control System, its Features and Applications”, 2004 5th Asian
Control Conference.
[10]. Purtojo, R. Akmeliawati and Wahyudi, “Two-parameter Compensator Design for Point-
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[11]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-of-Freedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
20
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[6]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-ofFreedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
[7]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
[8]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control
of a Multi degree of Freedom Flexible Joint Manipulator”,2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
[9]. Masanori Yukitomo, Takashi Shigemasa, Yasushi Baba, Fumia Kojima, “A Two
Degrees of Freedom PID Control System, its Features and Applications”, 2004 5th Asian
Control Conference.
[10]. Purtojo, R. Akmeliawati and Wahyudi, “Two-parameter Compensator Design for Point-
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[11]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-of-Freedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
20
1 out of 21
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





