Signals and System
VerifiedAdded on 2023/04/10
|20
|879
|362
AI Summary
This lab assignment focuses on understanding convolution and how to use it to design and analyze systems. It covers topics such as convolution, correlation, and template matching. The MATLAB program is used for signal manipulation and finding convolution of signals.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Signals and System 1
Signals and System
By
(Name)
(Course)
(Professor’s Name)
(Institution)
(State)
(Date)
Signals and System
By
(Name)
(Course)
(Professor’s Name)
(Institution)
(State)
(Date)
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Signals and System 2
Introduction
A signal is an explanation of how one constraint differs with another constraint. For example,
voltage shifting over time in an electronic circuit, or lustre varying with distance in an image
(Armstrong & Feldberg, 2015). A system is any procedure that yields an output signal in
reply to an input signal. Continuous systems input and output continuous signals, for instance
in analog electronics. Discrete systems input and output discrete signals, for instance
computer programs that control the values stored in arrays Godfrey, (2016).
Convolution describes the process of a signal passing through a linear, time-invariant system
defined by an impulse response (Lawson & Uhlenbeck, 2017). Convolution is a central
concept that describes every linear, time-invariant system that we create and use. Convolution
describes how the circuits affect a given voltage input, how radio waves travel through the
atmosphere, how to blur and sharpen images, how to recognize images/faces videos, etc.
While many of these systems do not use convolution directly (we often use faster algorithms
that indirectly perform convolution), understanding how and why convolution works is
essential to all of them (Pierce & Noll, 2015).
In this lab assignment, we will focus on understanding convolution and how to use it to
design and analyze systems. We will create several system impulse responses and study how
each system affects a given signal. We then study a widely used application of convolution,
known as “template matching” or “matched filtering,” that is often used to locate images,
radar or sonar signals, and musical segments in noisy data sets.
Objectives
This lab assignment has three learning objectives:
1. To improve your understanding of convolution.
2. To introduce you to the concept of correlation and template matching.
Introduction
A signal is an explanation of how one constraint differs with another constraint. For example,
voltage shifting over time in an electronic circuit, or lustre varying with distance in an image
(Armstrong & Feldberg, 2015). A system is any procedure that yields an output signal in
reply to an input signal. Continuous systems input and output continuous signals, for instance
in analog electronics. Discrete systems input and output discrete signals, for instance
computer programs that control the values stored in arrays Godfrey, (2016).
Convolution describes the process of a signal passing through a linear, time-invariant system
defined by an impulse response (Lawson & Uhlenbeck, 2017). Convolution is a central
concept that describes every linear, time-invariant system that we create and use. Convolution
describes how the circuits affect a given voltage input, how radio waves travel through the
atmosphere, how to blur and sharpen images, how to recognize images/faces videos, etc.
While many of these systems do not use convolution directly (we often use faster algorithms
that indirectly perform convolution), understanding how and why convolution works is
essential to all of them (Pierce & Noll, 2015).
In this lab assignment, we will focus on understanding convolution and how to use it to
design and analyze systems. We will create several system impulse responses and study how
each system affects a given signal. We then study a widely used application of convolution,
known as “template matching” or “matched filtering,” that is often used to locate images,
radar or sonar signals, and musical segments in noisy data sets.
Objectives
This lab assignment has three learning objectives:
1. To improve your understanding of convolution.
2. To introduce you to the concept of correlation and template matching.

Signals and System 3
3. To design your own “Name that tune” algorithm
Methodology
The MATLAB program was used to create the convolution for signal manipulation and the
program is shown below.
On completion of manipulation, the program was later used to find convolution of the the
signals.
Results and Discussions
Part A: Convolution for Signal Manipulation........................................................................1
Part B: Convolution for Finding Signals................................................................................8
Part three...............................................................................................................................15
Functions..............................................................................................................................16
clear;
clc;
close all;
Part A: Convolution for Signal Manipulation
part one: Signal creation
x=stepseq(3,0,20)-stepseq(8,0,20)-imseq(17,0,20);
n = 0:20;
stem(n,x);
xlabel('Samples');
ylabel('Amplitude');
grid on;
%part two: Convolve with a Delta Function
h=imseq(0,0,20);
y = conv(x,h);
length_of_y=length(y)
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
%part three: Convolve with a Shifted Delta Function
k=[5 6 10 19];
3. To design your own “Name that tune” algorithm
Methodology
The MATLAB program was used to create the convolution for signal manipulation and the
program is shown below.
On completion of manipulation, the program was later used to find convolution of the the
signals.
Results and Discussions
Part A: Convolution for Signal Manipulation........................................................................1
Part B: Convolution for Finding Signals................................................................................8
Part three...............................................................................................................................15
Functions..............................................................................................................................16
clear;
clc;
close all;
Part A: Convolution for Signal Manipulation
part one: Signal creation
x=stepseq(3,0,20)-stepseq(8,0,20)-imseq(17,0,20);
n = 0:20;
stem(n,x);
xlabel('Samples');
ylabel('Amplitude');
grid on;
%part two: Convolve with a Delta Function
h=imseq(0,0,20);
y = conv(x,h);
length_of_y=length(y)
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
%part three: Convolve with a Shifted Delta Function
k=[5 6 10 19];

Signals and System 4
for i=1:4
s=k(i);
h=imseq(s,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
% Part four: Convolve with Two Delta Function
k2=[19 17 14 11];
for i=1:4
s=k2(i);
h=imseq(0,0,20)-imseq(s,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
% Part five: Convolve with a Box (Running Averaging)
h=(1/3).*stepseq(0,0,20)-stepseq(3,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
% Part six: Convolve with a Di?erence (Edge Detection)
h=-imseq(0,0,20)+2.*stepseq(1,0,20)-imseq(2,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
for i=1:4
s=k(i);
h=imseq(s,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
% Part four: Convolve with Two Delta Function
k2=[19 17 14 11];
for i=1:4
s=k2(i);
h=imseq(0,0,20)-imseq(s,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
% Part five: Convolve with a Box (Running Averaging)
h=(1/3).*stepseq(0,0,20)-stepseq(3,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
% Part six: Convolve with a Di?erence (Edge Detection)
h=-imseq(0,0,20)+2.*stepseq(1,0,20)-imseq(2,0,20);
y = conv(x,h);
a = 0:length(y)-1;
figure;
stem(a,y);
xlabel('Samples');
ylabel('Amplitude');
grid on;
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Signals and System 5

Signals and System 6

Signals and System 7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Signals and System 8

Signals and System 9

Signals and System 10
Part B: Convolution for Finding Signals
Part one: Creating signals
Part B: Convolution for Finding Signals
Part one: Creating signals
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Signals and System 11
x1 = sin(pi/10*(0:19));
u1=plotting_i(x1);
x2 = sin(pi/5*(0:19));
u2=plotting_i(x2);
x3 = sin(pi/2*(0:19));
u3=plotting_i(x3);
x4 = (-1).^(0:19);
u4=plotting_i(x4);
% Part two: Concatenating signals
z = [x1 x2 x3 x4];
% Part three: The Auto-Correlation
[a1,b1]=plotting_a(x1);
[a2,b2]=plotting_a(x2);
[a3,b3]=plotting_a(x3);
[a4,b4]=plotting_a(x4);
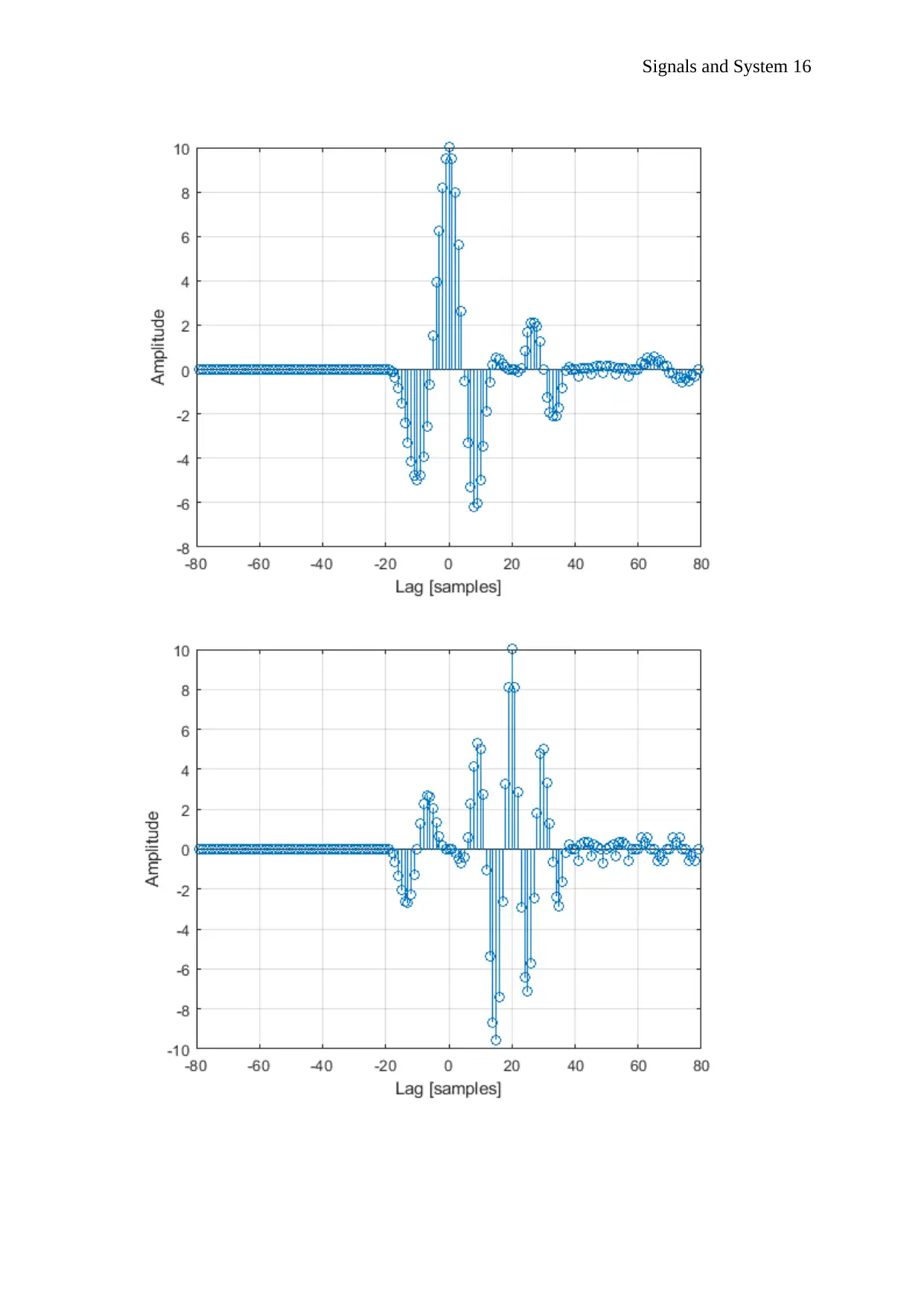
% Part four: The Cross-Correlation (Template Matching)
z1 = xcorr(z, x1);
t1=plotting_ii(z1);
z2 = xcorr(z, x2);
t2=plotting_ii(z2);
z3 = xcorr(z, x3);
t3=plotting_ii(z3);
z4 = xcorr(z, x4);
t4=plotting_ii(z4);
x1 = sin(pi/10*(0:19));
u1=plotting_i(x1);
x2 = sin(pi/5*(0:19));
u2=plotting_i(x2);
x3 = sin(pi/2*(0:19));
u3=plotting_i(x3);
x4 = (-1).^(0:19);
u4=plotting_i(x4);
% Part two: Concatenating signals
z = [x1 x2 x3 x4];
% Part three: The Auto-Correlation
[a1,b1]=plotting_a(x1);
[a2,b2]=plotting_a(x2);
[a3,b3]=plotting_a(x3);
[a4,b4]=plotting_a(x4);
% Part four: The Cross-Correlation (Template Matching)
z1 = xcorr(z, x1);
t1=plotting_ii(z1);
z2 = xcorr(z, x2);
t2=plotting_ii(z2);
z3 = xcorr(z, x3);
t3=plotting_ii(z3);
z4 = xcorr(z, x4);
t4=plotting_ii(z4);

Signals and System 12

Signals and System 13
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Signals and System 14

Signals and System 15
Signals and System 16
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Signals and System 17

Signals and System 18
Part three
[y, Fs] = audioread(['Peter_Rudenko.mp3']);
t = 1/Fs:1/Fs:length(y)/Fs;
plot(t, y);
xlabel('Time [sec]')
ylabel('Amplitude')
grid on;
%sound(y, Fs)
Functions
function [x,n]=imseq(n0,n1,n2) %Impulse signal
n=[n1:n2];
x=[(n-n0)==0];
end
function [x,n]=stepseq(n0,n1,n2)%Step signal
n=[n1:n2];
x=[(n-n0)>=0];
end
function n=plotting_i(p)%Convolution for Finding Signals
n=0:19;
figure;
stem(n,p);
Part three
[y, Fs] = audioread(['Peter_Rudenko.mp3']);
t = 1/Fs:1/Fs:length(y)/Fs;
plot(t, y);
xlabel('Time [sec]')
ylabel('Amplitude')
grid on;
%sound(y, Fs)
Functions
function [x,n]=imseq(n0,n1,n2) %Impulse signal
n=[n1:n2];
x=[(n-n0)==0];
end
function [x,n]=stepseq(n0,n1,n2)%Step signal
n=[n1:n2];
x=[(n-n0)>=0];
end
function n=plotting_i(p)%Convolution for Finding Signals
n=0:19;
figure;
stem(n,p);

Signals and System 19
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
function [a,b]=plotting_a(x) %The Auto-Correlation
a = conv(fliplr(x), x);
b = xcorr(x, x);
n = -(20-1):(20-1); % 10 is from the maximum length between x1 and h
figure;
stem(n,a)
xlabel('Lag [samples]')
ylabel('Amplitude')
grid on;
end
function n=plotting_ii(z) %The Cross-Correlation (Template Matching)
n = -(80-1):(80-1); % 40 is from the maximum length between z and h
figure;
stem(n, z)
xlabel('Lag [samples]')
ylabel('Amplitude')
grid on;
end
length_of_y =
41
Published with MATLAB® R2018b
Conclusion
In conclusion, the concept we were able to comprehensively understand convolution and how
to use it to design and analyze systems. We successfully created several system impulse
responses and studied how each system affects a particular signal.
xlabel('Samples');
ylabel('Amplitude');
grid on;
end
function [a,b]=plotting_a(x) %The Auto-Correlation
a = conv(fliplr(x), x);
b = xcorr(x, x);
n = -(20-1):(20-1); % 10 is from the maximum length between x1 and h
figure;
stem(n,a)
xlabel('Lag [samples]')
ylabel('Amplitude')
grid on;
end
function n=plotting_ii(z) %The Cross-Correlation (Template Matching)
n = -(80-1):(80-1); % 40 is from the maximum length between z and h
figure;
stem(n, z)
xlabel('Lag [samples]')
ylabel('Amplitude')
grid on;
end
length_of_y =
41
Published with MATLAB® R2018b
Conclusion
In conclusion, the concept we were able to comprehensively understand convolution and how
to use it to design and analyze systems. We successfully created several system impulse
responses and studied how each system affects a particular signal.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Signals and System 20
Reference
Armstrong, P.,& Feldberg, G. (2015). Take Care: Warning Signals for Canada's Health
System. Toronto, University of Toronto Press. Available from:
http://public.eblib.com/choice/publicfullrecord.aspx?p=4931224. (Date of Access: 23rd,
March, 2019)
Godfrey, K. (2016). Perturbation signals for system identification. New York, Prentice Hall.
Lawson, J. L., & Uhlenbeck, G. E. (2017). Threshold signals. New York, McGraw-Hill.
Pierce, J. R., & Noll, A. M. (2015). Signals: the science of telecommunications. New York,
Scientific American Library.
Reference
Armstrong, P.,& Feldberg, G. (2015). Take Care: Warning Signals for Canada's Health
System. Toronto, University of Toronto Press. Available from:
http://public.eblib.com/choice/publicfullrecord.aspx?p=4931224. (Date of Access: 23rd,
March, 2019)
Godfrey, K. (2016). Perturbation signals for system identification. New York, Prentice Hall.
Lawson, J. L., & Uhlenbeck, G. E. (2017). Threshold signals. New York, McGraw-Hill.
Pierce, J. R., & Noll, A. M. (2015). Signals: the science of telecommunications. New York,
Scientific American Library.
1 out of 20
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





