Simulation and Analysis of PID Controller in 2DOF System

A comprehensive simulation of a 2DOF system with a PID controller was performed in Simulink, exploring the effects of drag coefficient, air density, and velocity on aerodynamics. The simulation also analyzed the Equivalent inertial force during acceleration and ground wheel friction requirements. Additionally, the discussion covers the advantages and characteristics of the PID controller, including its components (Kp, Ki, Kd) and transfer function analysis. Furthermore, system identification was performed using a nonlinear Simulink model with forced data, testing the model's response to hypothetical force inputs and implicit/explicit modeling approaches.

Introduction
The simulation of PID controller and various conditions of the system will be developed in
matlab Simulink. The step response and bode plot are will be calculated by linear analysis tool.
The performance and characteristics of the controller is specified. Simulation of the ramp of
2DOF output will be demonstrated in the matlab files. The stability and frequency response of
the transfer function will be plotted. The Simulink model of non-linear and testing the model
with forced input will be evaluated.
1 – Stunt Control:
Minimum Scope Areas
1. Simulink of PID controllers
The above diagram shows that the simulation for PID controller in Simulink. The transfer
function is used in this PID controller to obtain the output. PID controller consists of two parts,
namely Controller and power plant. In the controller session, Proportional controller, Integral
controller and Derivative controller are connected by sum operation. The transfer function, gain
and parameters are built in power plant. In the PID controller some values are assumed to get
output.the controller values and transfer function are Kp=6, Ki=1, Kd=1 and n=[1 6 10],
d=[1 0 7 1]. The simulation for the PID controllers is done by linear analysis tool for various

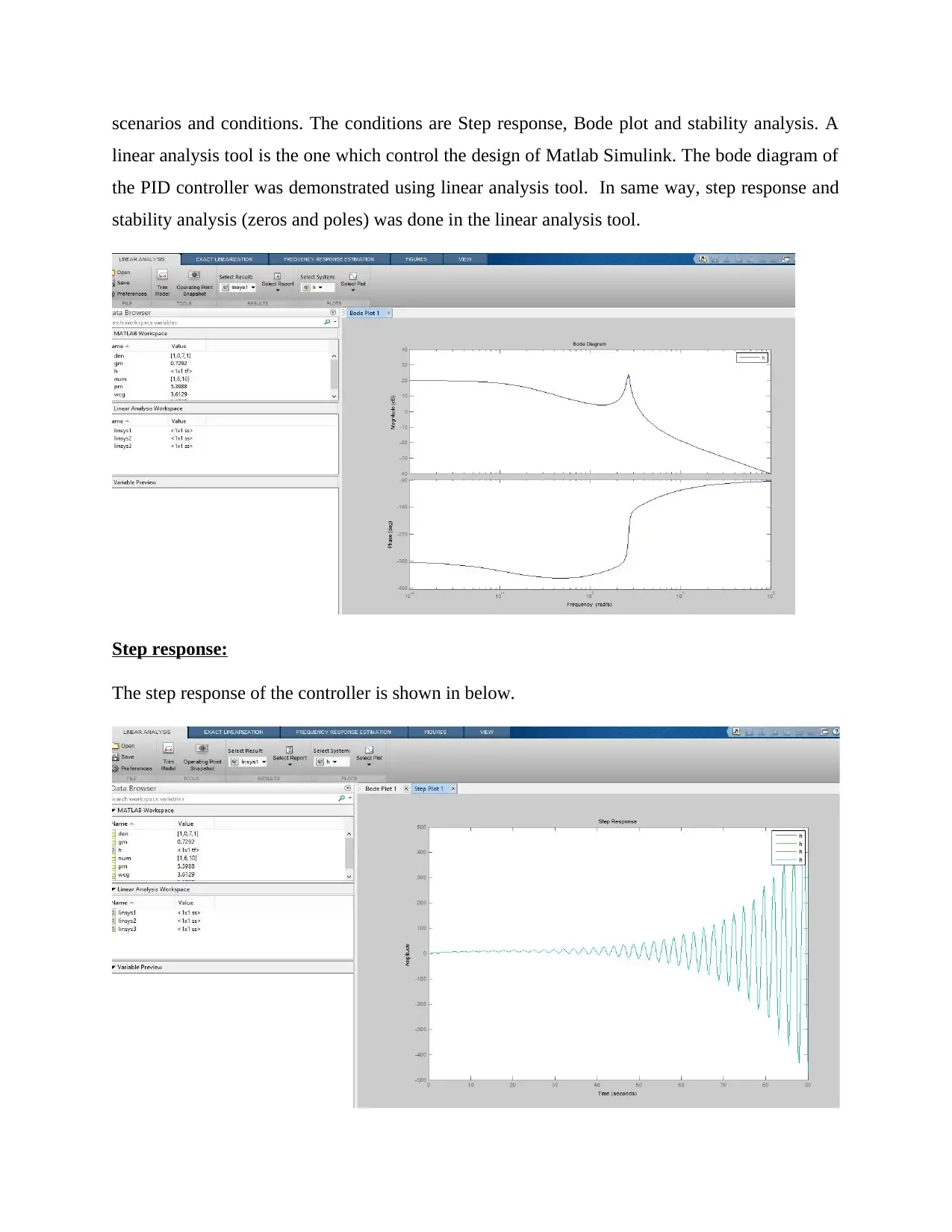
scenarios and conditions. The conditions are Step response, Bode plot and stability analysis. A
linear analysis tool is the one which control the design of Matlab Simulink. The bode diagram of
the PID controller was demonstrated using linear analysis tool. In same way, step response and
stability analysis (zeros and poles) was done in the linear analysis tool.
Step response:
The step response of the controller is shown in below.

Stability (zeros and poles)
The zeros and poles of the controller is represented in this picture.
2DOF PID Controller Simulation
The two degree of freedom with PID controller is shown in above screenshot. The Step input
signal is given into the PID controller. Transfer function is connected to the PID controller and

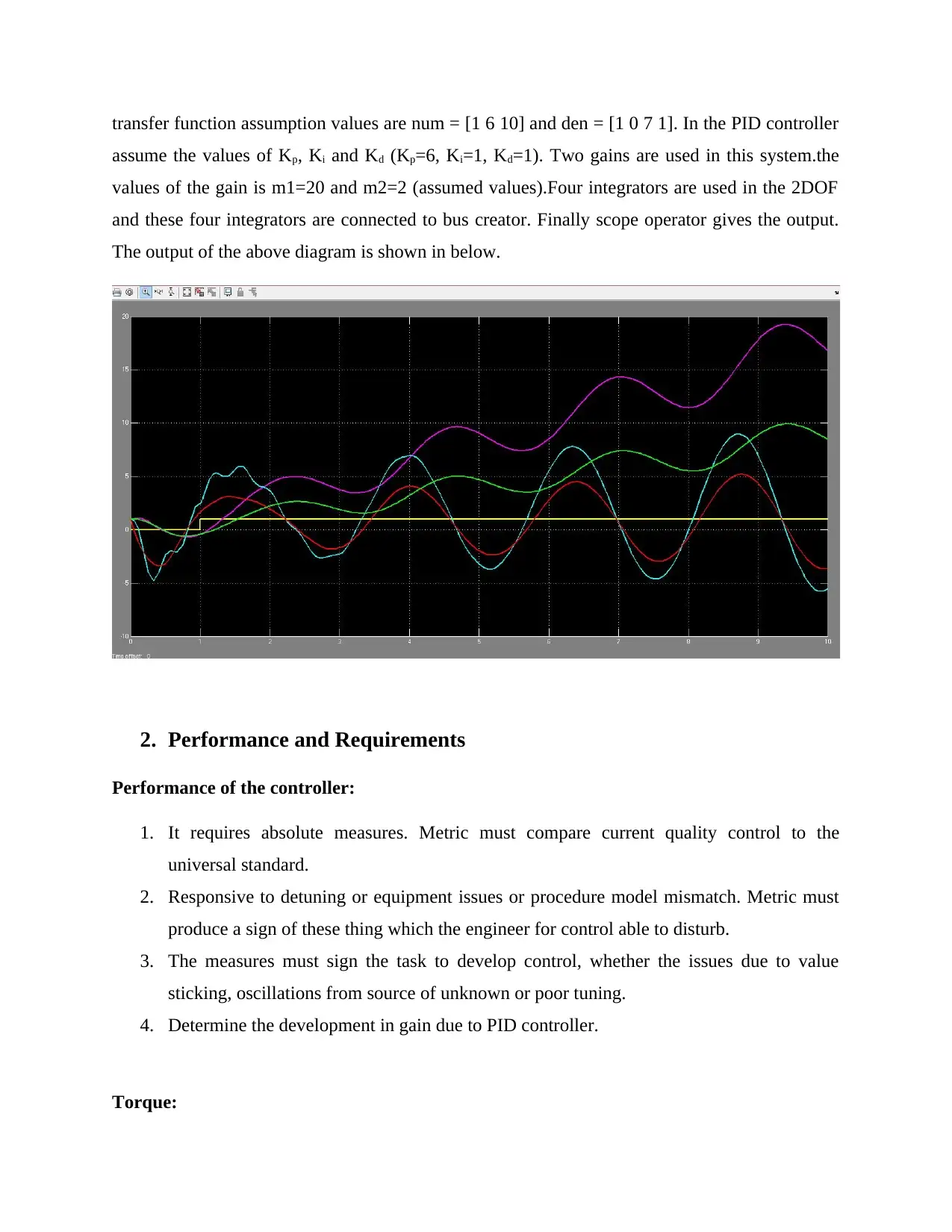
transfer function assumption values are num = [1 6 10] and den = [1 0 7 1]. In the PID controller
assume the values of Kp, Ki and Kd (Kp=6, Ki=1, Kd=1). Two gains are used in this system.the
values of the gain is m1=20 and m2=2 (assumed values).Four integrators are used in the 2DOF
and these four integrators are connected to bus creator. Finally scope operator gives the output.
The output of the above diagram is shown in below.
2. Performance and Requirements
Performance of the controller:
1. It requires absolute measures. Metric must compare current quality control to the
universal standard.
2. Responsive to detuning or equipment issues or procedure model mismatch. Metric must
produce a sign of these thing which the engineer for control able to disturb.
3. The measures must sign the task to develop control, whether the issues due to value
sticking, oscillations from source of unknown or poor tuning.
4. Determine the development in gain due to PID controller.
Torque:

Torque is the basic quantity that helps to describe the function of rotating machinery. In the
applications of adjustable speed drive, performance is described which in terms of torque and
other parameters. The torque is an expression of force which is applied to turn the shaft. The net
torque which acts on the wheel separated by the moment of inertia equivalent to the angular
acceleration of the wheel. The net torque consisting of torque of shaft from engine that is resist
by torque of brake and components due to viscous friction of the wheel and tractive force of the
tire.
Horse power:
It is not the basic parameter, but it is the power calculation which is consumed while a definite
quantity of torque is utilized to turn the shaft at a definite speed.
Horse power= (Torque *RPM)/5252
The requirements of the motor tractive torque should be equivalent to the tractive torque at the
wheel. That is tractive torque which is equivalent to the multiplication of tractive force and the
mean radius of the wheel.
Tw=Ft*rw
Here,
rw is the effective mean radius of the wheel
Ft is the sum of Fr, Fg, Fd, and Fie
Fr is the rolling resistance of the tire
Fg is the forces because of the gradient which is depends on angle of slope
Fd is the aerodynamics drag as the function of drag coefficient, air density, squared of velocity of
vehicle and cross sectional area of vehicle
Fie is the Equivalent inertial force during acceleration which includes rotational and linear
inertias because of the mass of vehicle and gear wheel rotating component.
It also include the net efficiency of transmission to reach the speed for the power in hp.
3. Ground wheel Friction Requirements

The wheel point in contact with ground has no relative motion. Suppose the load directly
contacts to the ground, the wheel removes the huge force due to friction which is rise. Hence,
some of the resistance exist in the motion of wheel. The causes for the resistance is due to blend
of friction at rim and axle and the ground and wheel deform with effects which contacts in
between ground and wheel.
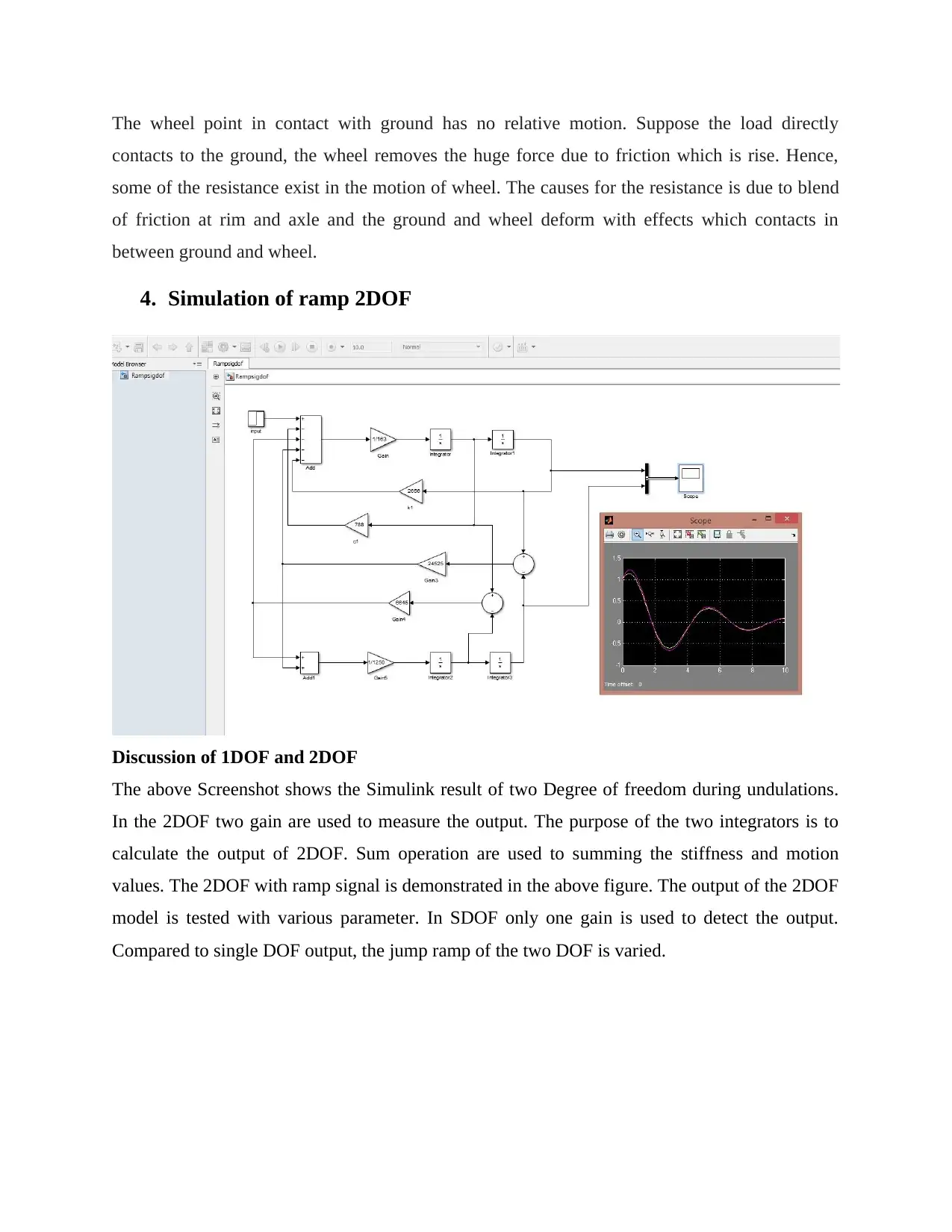
4. Simulation of ramp 2DOF
Discussion of 1DOF and 2DOF
The above Screenshot shows the Simulink result of two Degree of freedom during undulations.
In the 2DOF two gain are used to measure the output. The purpose of the two integrators is to
calculate the output of 2DOF. Sum operation are used to summing the stiffness and motion
values. The 2DOF with ramp signal is demonstrated in the above figure. The output of the 2DOF
model is tested with various parameter. In SDOF only one gain is used to detect the output.
Compared to single DOF output, the jump ramp of the two DOF is varied.

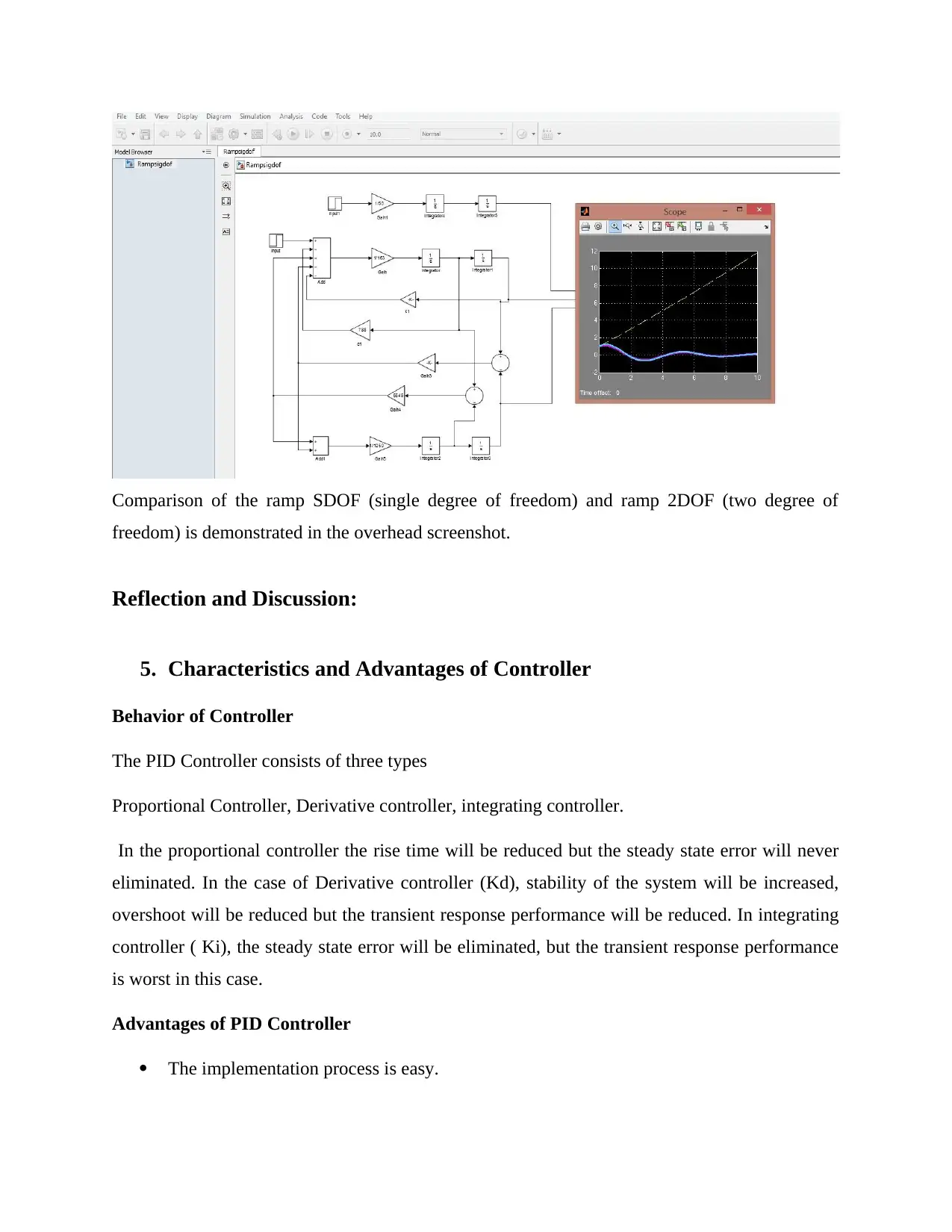
Comparison of the ramp SDOF (single degree of freedom) and ramp 2DOF (two degree of
freedom) is demonstrated in the overhead screenshot.
Reflection and Discussion:
5. Characteristics and Advantages of Controller
Behavior of Controller
The PID Controller consists of three types
Proportional Controller, Derivative controller, integrating controller.
In the proportional controller the rise time will be reduced but the steady state error will never
eliminated. In the case of Derivative controller (Kd), stability of the system will be increased,
overshoot will be reduced but the transient response performance will be reduced. In integrating
controller ( Ki), the steady state error will be eliminated, but the transient response performance
is worst in this case.
Advantages of PID Controller
 The implementation process is easy.

 PID controller is mainly used for transient response, such as oscillation, overshoot and
settling time.
 The PID controller is a way to control a variety of environmental conditions, from
temperature to speed
 PID controller is having all time estimation.
 It is widely used and more robustness and feasibility.
Components of PID Controller
There are mainly three components are used in PID controller. These three components are
inbuilt option with PID controller tool in the Simulink model.
Kp - Proportional control
Ki - Integral control
Kd - Derivative controller
Integrator and Sum operation are also used in the PID controller Simulink.
6. Assumptions of the Simulation
The transfer function is assumed to analyses the PID controller Performance in Simulation
Let assume the numerator and denominator values to make the transfer function.
Numerator= [1 6 10]
Denominator= [1 0 7 1]
The transfer function of the above value is,
T . F= s2+6 s+ 10
s3+ 7 s +1
In the Matlab window, G=tf(num,den) command is used built a transfer function. In PID
controller kp, ki and kd values are also assumed to get the output. The values of these parameter
is Kp=6, ki=1 and kd=1.

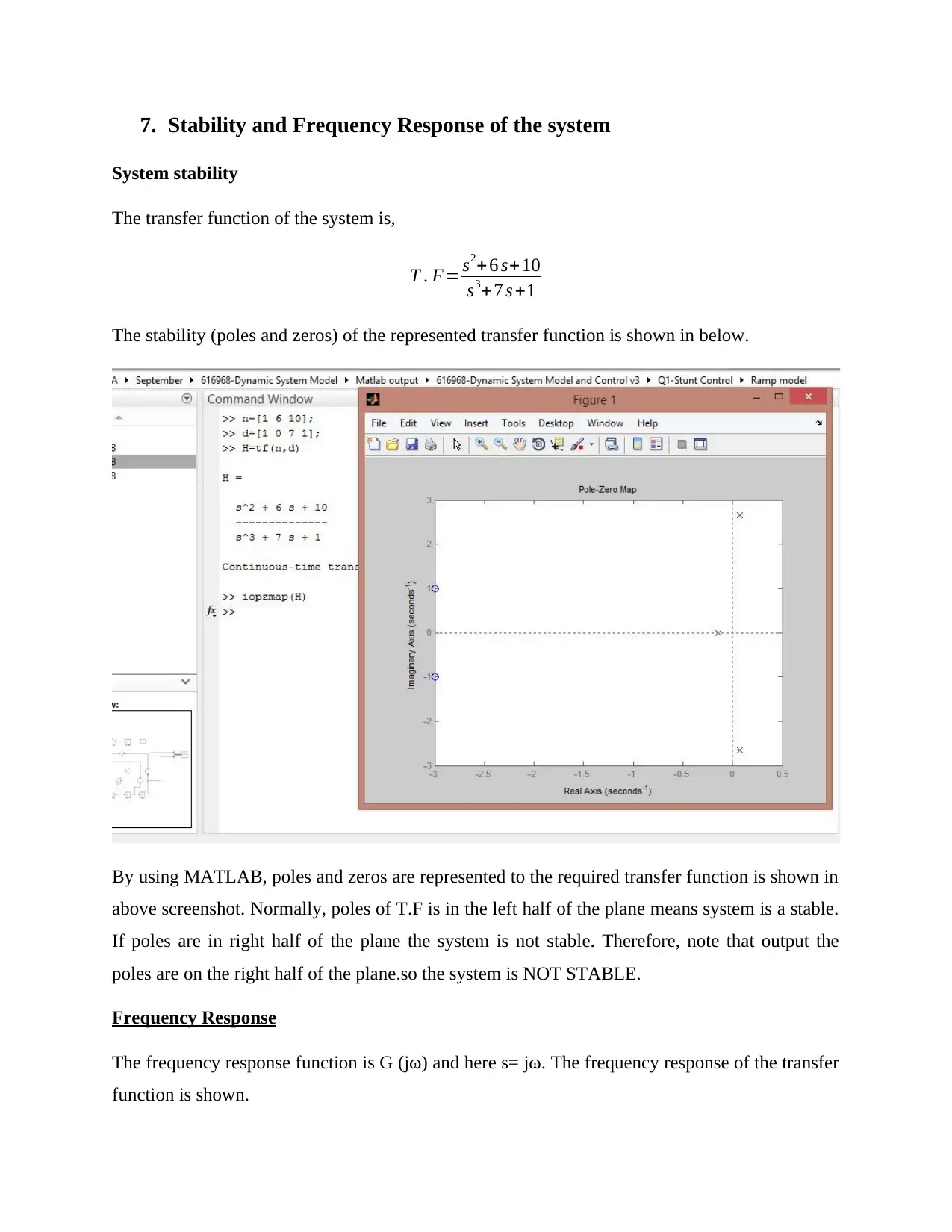
7. Stability and Frequency Response of the system
System stability
The transfer function of the system is,
T . F= s2+6 s+ 10
s3+ 7 s +1
The stability (poles and zeros) of the represented transfer function is shown in below.
By using MATLAB, poles and zeros are represented to the required transfer function is shown in
above screenshot. Normally, poles of T.F is in the left half of the plane means system is a stable.
If poles are in right half of the plane the system is not stable. Therefore, note that output the
poles are on the right half of the plane.so the system is NOT STABLE.
Frequency Response
The frequency response function is G (jω) and here s= jω. The frequency response of the transfer
function is shown.

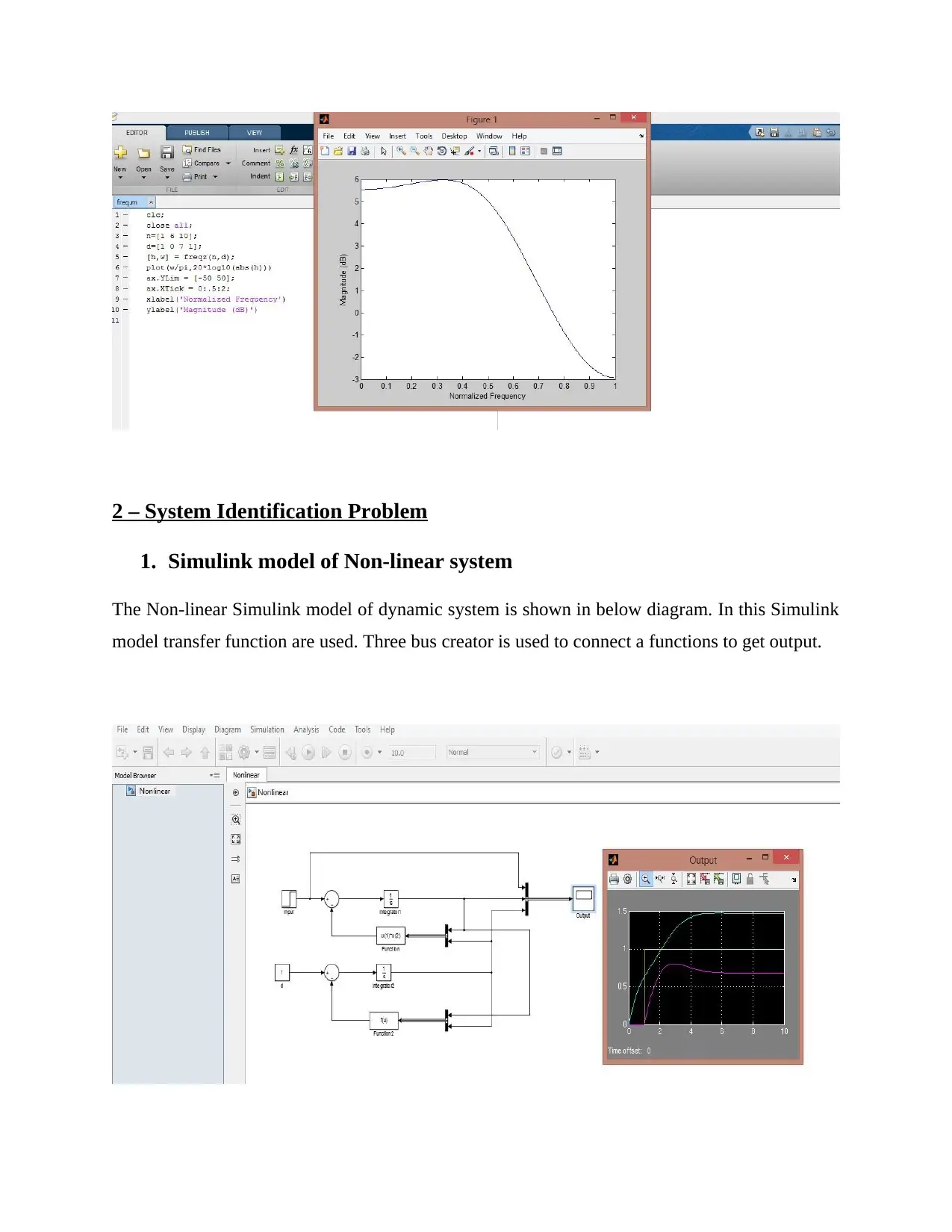
2 – System Identification Problem
1. Simulink model of Non-linear system
The Non-linear Simulink model of dynamic system is shown in below diagram. In this Simulink
model transfer function are used. Three bus creator is used to connect a functions to get output.

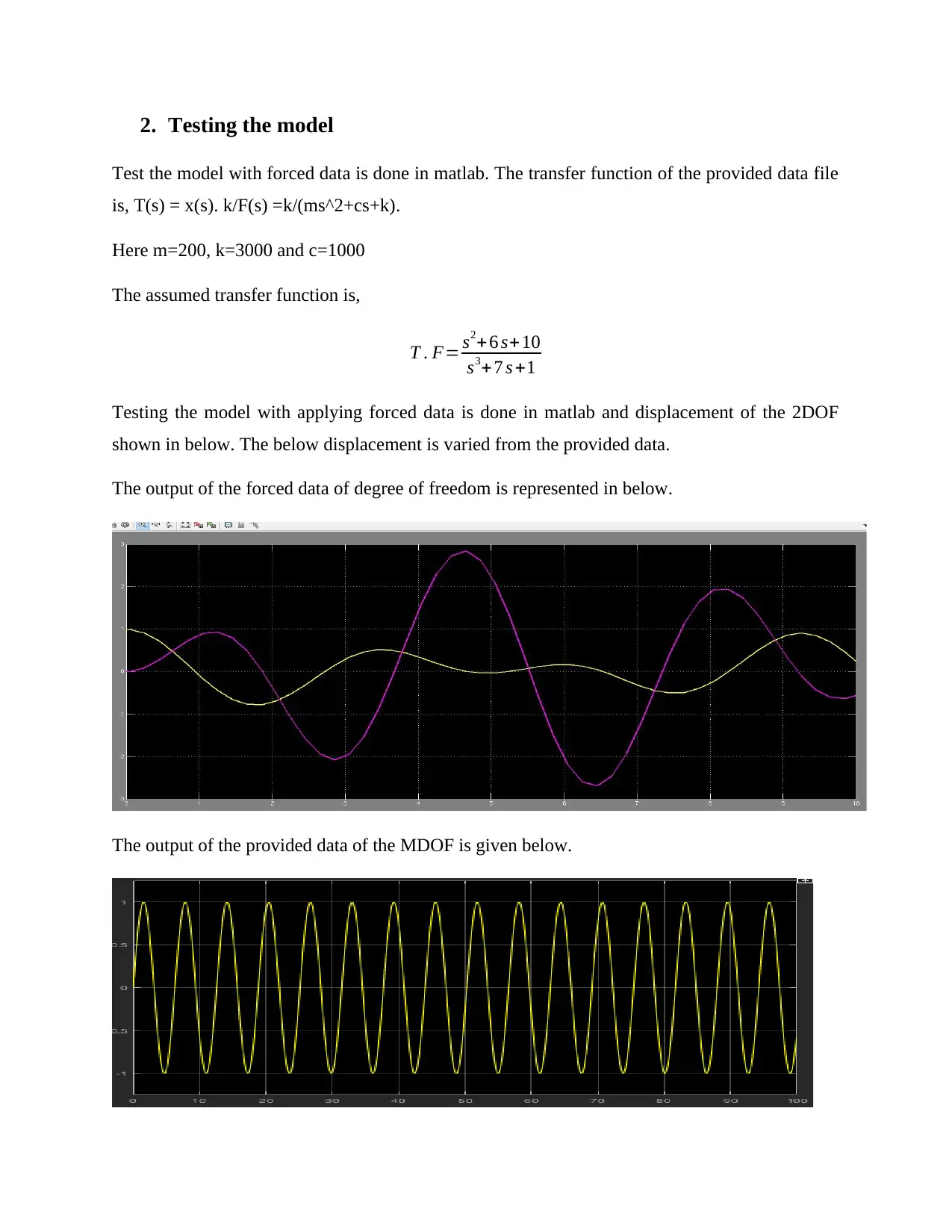
2. Testing the model
Test the model with forced data is done in matlab. The transfer function of the provided data file
is, T(s) = x(s). k/F(s) =k/(ms^2+cs+k).
Here m=200, k=3000 and c=1000
The assumed transfer function is,
T . F= s2+6 s+ 10
s3+ 7 s +1
Testing the model with applying forced data is done in matlab and displacement of the 2DOF
shown in below. The below displacement is varied from the provided data.
The output of the forced data of degree of freedom is represented in below.
The output of the provided data of the MDOF is given below.

Hypothetical Force Inputs
The hypothetical force input is giving into the Simulink model the output of the
dynamic system is changed.
Implicit and Explicit model
No effects of damping or mass presented in static analysis. The nodal forces with damping and
mass are included in dynamic analysis. The static analysis can developed by using implicit
solver. By using explicit solver, the dynamic analysis is able to done. The solution of every step
needs iteration that is series of trial solution to accomplish equilibrium in a definite tolerance in
nonlinear implicit analysis. There is no iteration is needed in the explicit analysis. Because nodal
acceleration are resolved straightly. In explicit analysis, time step should be less than courant
time step. There is no implicit limit on size of time step in implicit transient analysis. The time
steps of implicit are usually various orders of magnitude which is higher than the time steps of
explicit.
Conclusion
The simulation of the PID controller of 2DOF has been done in matlab Simulink. The step
response and bode plot of the system has been plotted by using linear analysis tool. The
performance parameters and characteristics of the controller has been discussed. The frequency
response stability and of the transfer function has been analyzed. The Simulation model of the
non-linear system has been developed.

References
Corless, M. (2017). [online] Available at: http://www.hamilton.ie/ollie/Downloads/Dyn.pdf
[Accessed 25 Sep. 2017].
Holmberg, U. (2017). [online] Available at:
http://www.hh.se/download/18.7502f6fd13ccb4fa8cb2f6/1360676928481/PID.pdf
[Accessed 25 Sep. 2017].
Róbert, S. (2017). [online] Available at: http://hadmernok.hu/2009_4_szabolcsi.pdf [Accessed
25 Sep. 2017].