Statistical Research and Data Analysis: A Guide for Computing Assignments

This article provides a comprehensive guide to statistical research and data analysis for computing assignments. It covers topics such as variables, summary statistics, pivot tables, scatter diagrams, confidence intervals, and hypothesis testing. The guide includes examples and explanations to help students understand the concepts better. The article also highlights the importance of using computers for data analysis when dealing with large datasets. Course code, course name, and college/university are not mentioned.

COMPUTING ASSIGNMENT
Waleed Usman
Student Number: 11700685
Allocated Sample: 449

Section 1
The process of statistical research is driven from dataset which consists of variables. Variables
are dynamic elements which tend to change the value. These dataset contain data captured
through requisite symbols and also highlight the values assumed. In order to ascertain the
underlying the underlying relationship and association, it is imperative to explore the variables
provided. These relationships and other summary of variables can also be found using computers
as a suitable aid mechanism (Flick, 2015).
The following data can be used as an example to illustrate the same.
The summary statistics for the above data can be found with the aid of Data Analysis option that
excel presents.
1

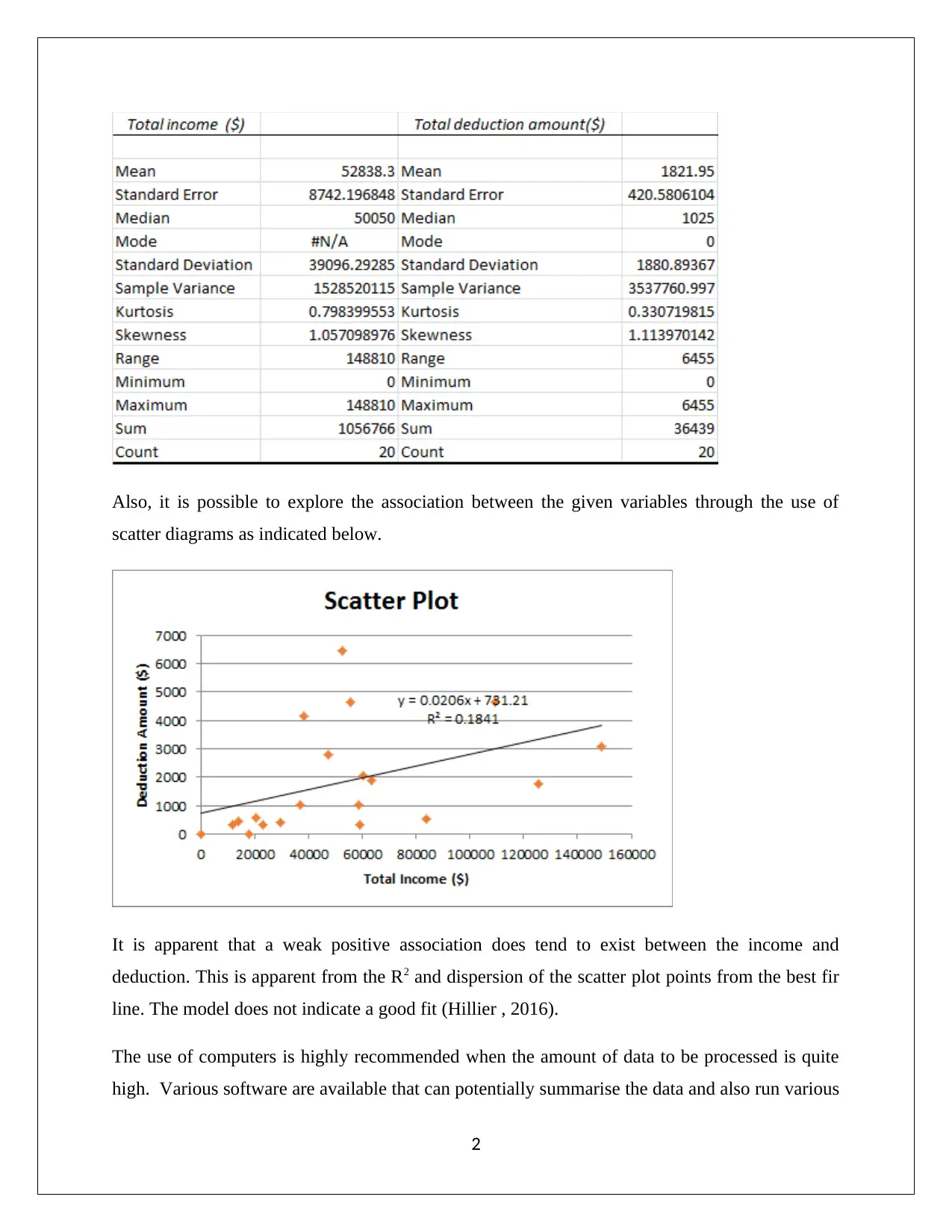
Also, it is possible to explore the association between the given variables through the use of
scatter diagrams as indicated below.
It is apparent that a weak positive association does tend to exist between the income and
deduction. This is apparent from the R2 and dispersion of the scatter plot points from the best fir
line. The model does not indicate a good fit (Hillier , 2016).
The use of computers is highly recommended when the amount of data to be processed is quite
high. Various software are available that can potentially summarise the data and also run various
2

inferential techniques so as to derive meaningful conclusions about the population (Hair et. al.,
2015).
Section 2
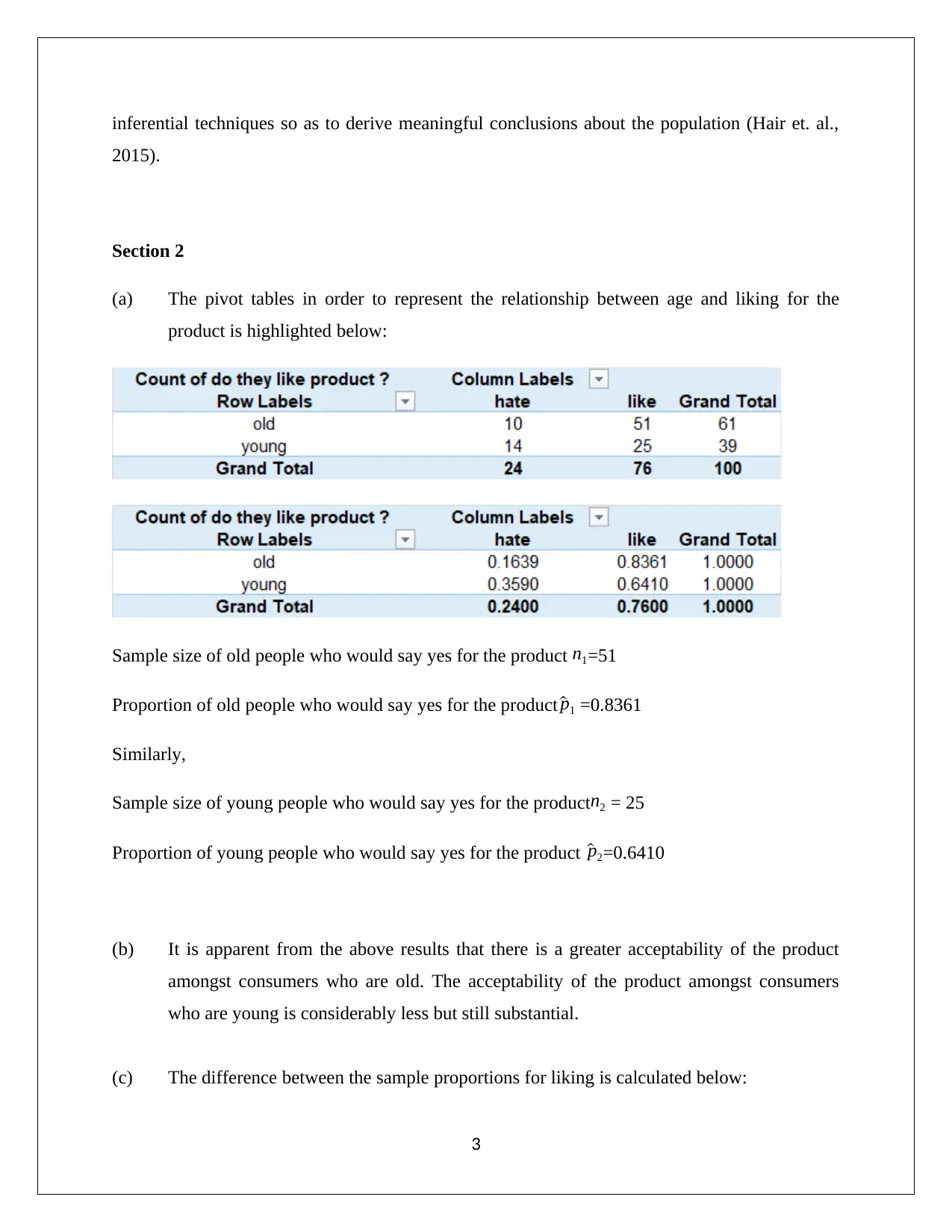
(a) The pivot tables in order to represent the relationship between age and liking for the
product is highlighted below:
Sample size of old people who would say yes for the product n1=51
Proportion of old people who would say yes for the product ^p1 =0.8361
Similarly,
Sample size of young people who would say yes for the productn2 = 25
Proportion of young people who would say yes for the product ^p2=0.6410
(b) It is apparent from the above results that there is a greater acceptability of the product
amongst consumers who are old. The acceptability of the product amongst consumers
who are young is considerably less but still substantial.
(c) The difference between the sample proportions for liking is calculated below:
3

^p1=0.8361
^p2=0.6410
Now,
Difference between the sample proportions ¿ ^p1− ^p2
^p1− ^p2=0.8361−0.6410=0.1950
Section 3
(a) The summary statistics for the sample is highlighted below:
For Old people
Sample size n1=61
Sample average x1=2.664
Sample standard deviation s1=1.094
For young people
Sample size n2 =39
Sample average x2=2.138
Sample standard deviation s2=1.412
4

(b) The average money that the old customers would pay would be higher than the
corresponding amount that young customers would pay. Also, the deviation trends seem
to be lesser for old customers as compared to young customers.
(c) Difference between the sample means x1−x2
μ1−μ2=x1 −x2=2.664−2.136
μ1−μ2=0.5280
Section 4
Data sample
(a) Scatter Plot
5

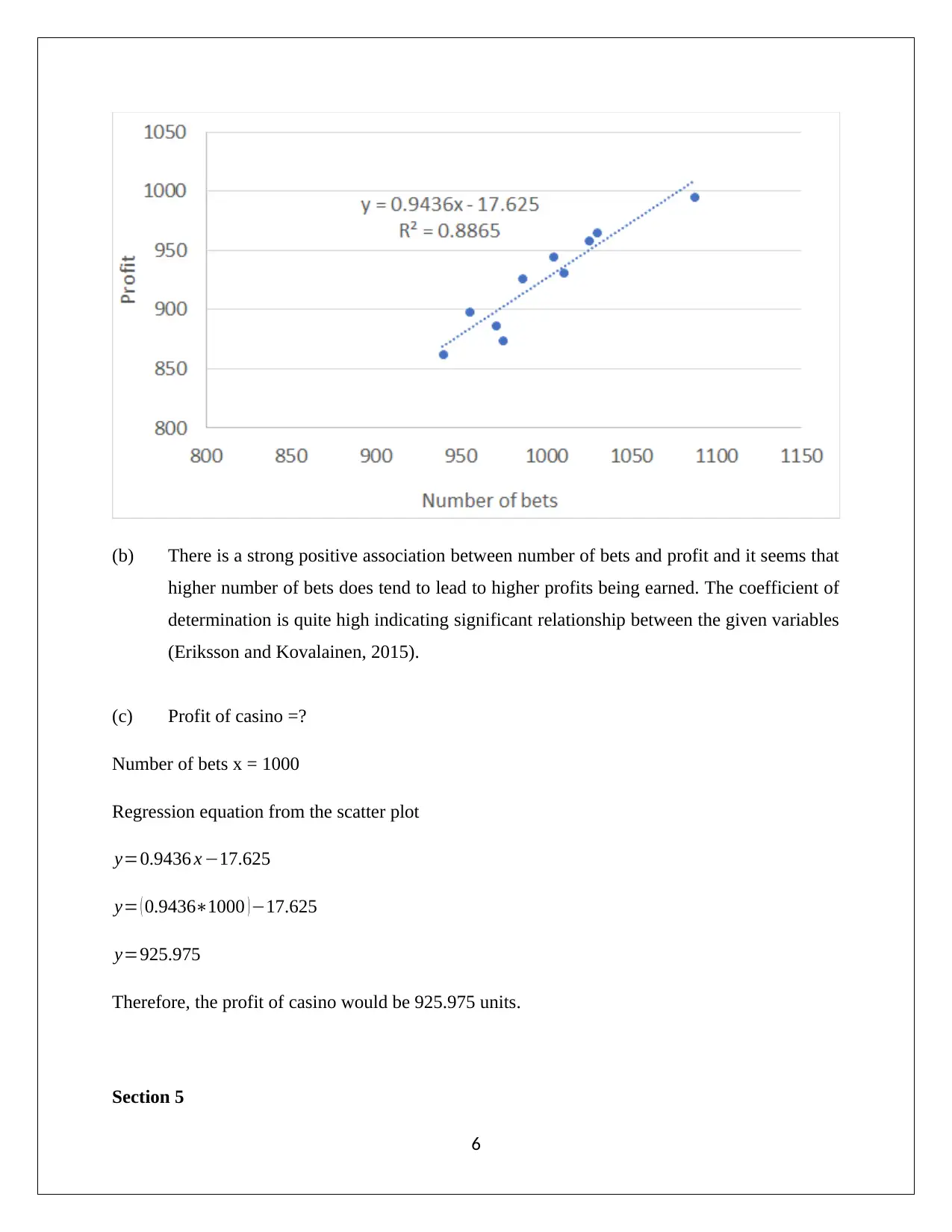
(b) There is a strong positive association between number of bets and profit and it seems that
higher number of bets does tend to lead to higher profits being earned. The coefficient of
determination is quite high indicating significant relationship between the given variables
(Eriksson and Kovalainen, 2015).
(c) Profit of casino =?
Number of bets x = 1000
Regression equation from the scatter plot
y=0.9436 x −17.625
y= ( 0.9436∗1000 )−17.625
y=925.975
Therefore, the profit of casino would be 925.975 units.
Section 5
6

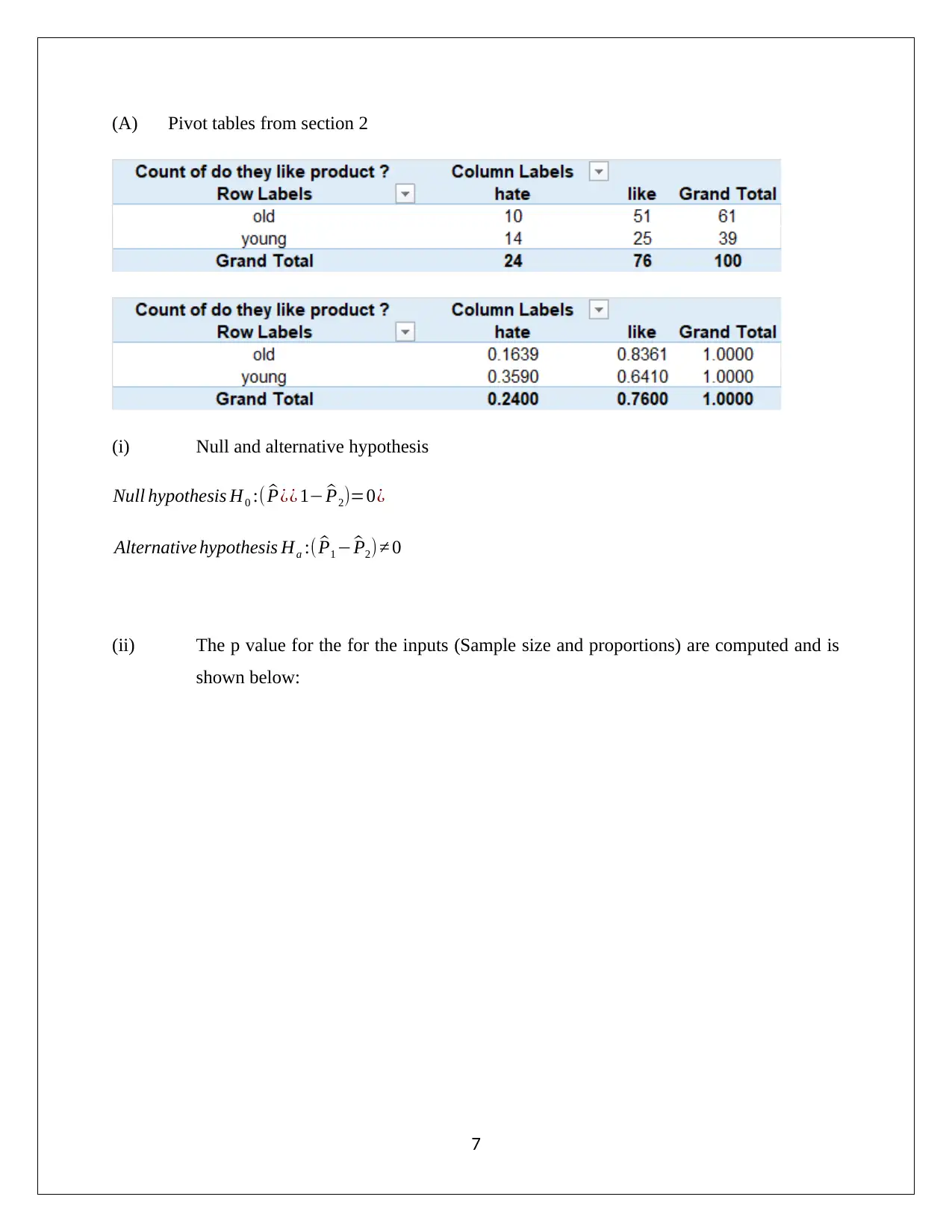
(A) Pivot tables from section 2
(i) Null and alternative hypothesis
Null hypothesis H0 :( ^P¿¿ 1− ^P2)=0¿
Alternative hypothesis Ha :( ^P1 − ^P2) ≠ 0
(ii) The p value for the for the inputs (Sample size and proportions) are computed and is
shown below:
7

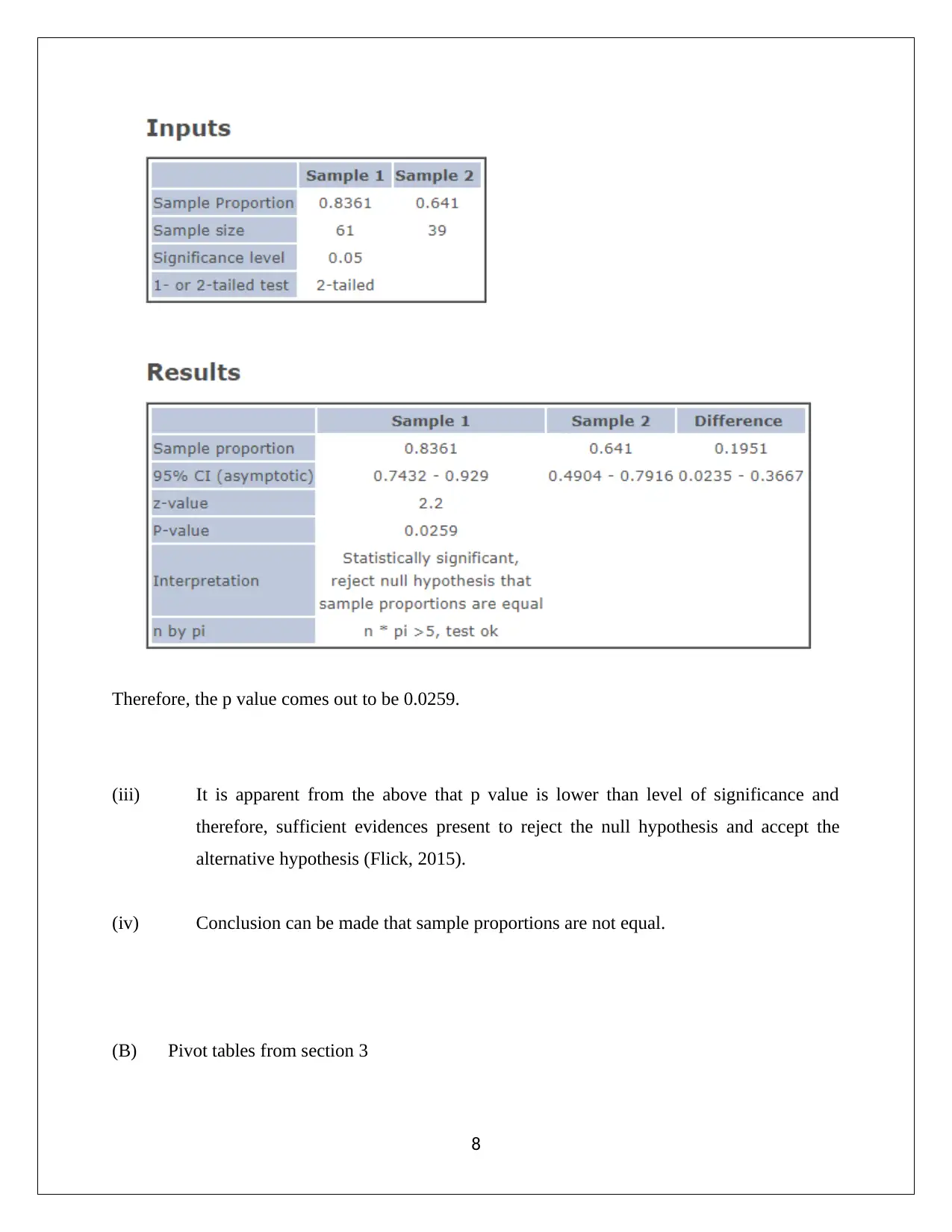
Therefore, the p value comes out to be 0.0259.
(iii) It is apparent from the above that p value is lower than level of significance and
therefore, sufficient evidences present to reject the null hypothesis and accept the
alternative hypothesis (Flick, 2015).
(iv) Conclusion can be made that sample proportions are not equal.
(B) Pivot tables from section 3
8

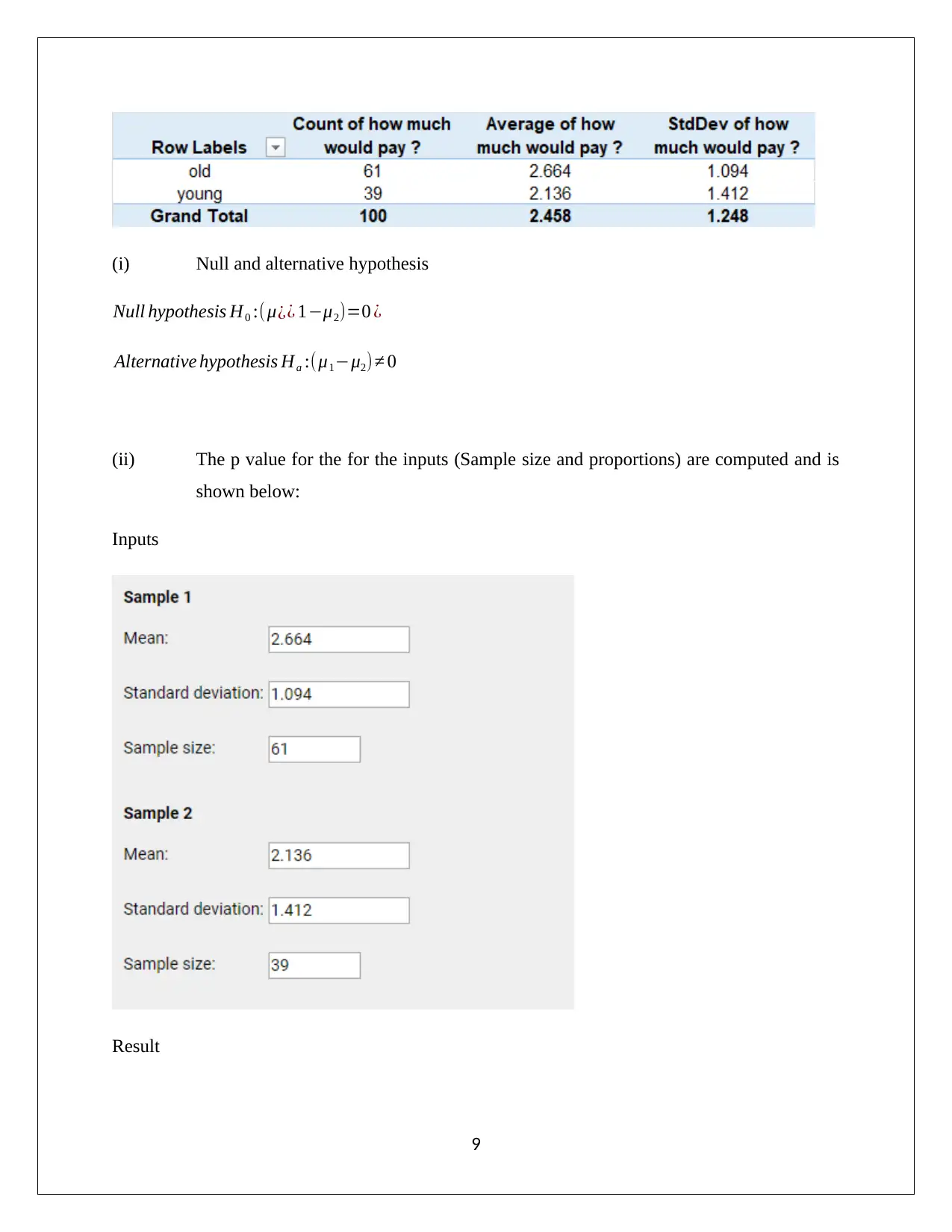
(i) Null and alternative hypothesis
Null hypothesis H0 :( μ¿¿ 1−μ2)=0 ¿
Alternative hypothesis Ha :(μ1−μ2)≠ 0
(ii) The p value for the for the inputs (Sample size and proportions) are computed and is
shown below:
Inputs
Result
9

The p value from the above comes out to be 0.0384.
(iii) Assuming level of significance = 5%
(iv) It can be seen that p value is lower than level of significance and therefore, sufficient
evidences present to reject the null hypothesis and to accept the alternative hypothesis
(Eriksson and Kovalainen, 2015).
(v) Conclusion can be made that sample means are not equal.
Section 6
(a) The numerical summary in the form of pivot table of the sample is highlighted below:
(b)
Sample size = 214
Number of people who will support the proposed change and will say yes = 128
10

Requisite proportion ^p= 128
214 =0.5981
(c) 90% confidence interval for proportion
Standard error ¿ √ 0.598 ( 1−0.598 )
214 =0.0335
The z value for 90% confidence interval = 1.645
Hence,
Lower limit =Proportion− ( z value∗Standard error )=0.5981− ( 1.645∗0.0335 )=0.543
Upper limit =Proportion+ ( z value∗Standard error )=0.5981+ (1.645∗0.0335 ) =0.653
Therefore, the 90% confidence interva [0.543 0.653].
Section 7
a) An example of a back to back histogram is indicated below.
11

b) The given histogram provides a monthly comparison of unemployment rates that prevail in
two cities namely Texas and California. The given variable is quantitative in nature
considering this variable is captured through numerical data.
c) The relationship between the two variables is weak considering the changes in the
unemployment witnessed in the two cities. This is because the unemployment may be the
result of domestic factor or international factors. If the unemployment is on account of
international factors, then the correlation would be higher but it would not be the case when
localised or regional factors are in play (Hillier, 2016).
d) The information indicated in the histogram and above discussion is relevant for business
decision making. This is imperative from the fact that there are some months witnessed in
California where the unemployment was in excess of 10% which would auger well for a
employer to set up a business consider that the requisite skills sets are available with the
labour force but there is a lack of opportunity (Hair et. al., 2015).
e) From the discussion in section 1, the above information can be used to draw association
between the two cities unemployment and therefore make prediction about the future
unemployment and the implications of the same on the business especially if it is located In
one of the cities mentioned (Eriksson and Kovalainen, 2015).
Section 8
(A) Using section 2
^p1− ^p2=0.8361−0.6410=0.1950
(i) The z score
^p1− ^p2 ¿ 0.1950
Average of the estimates (μ) = 0.14
Standard deviation (σ ) = 0.088
12

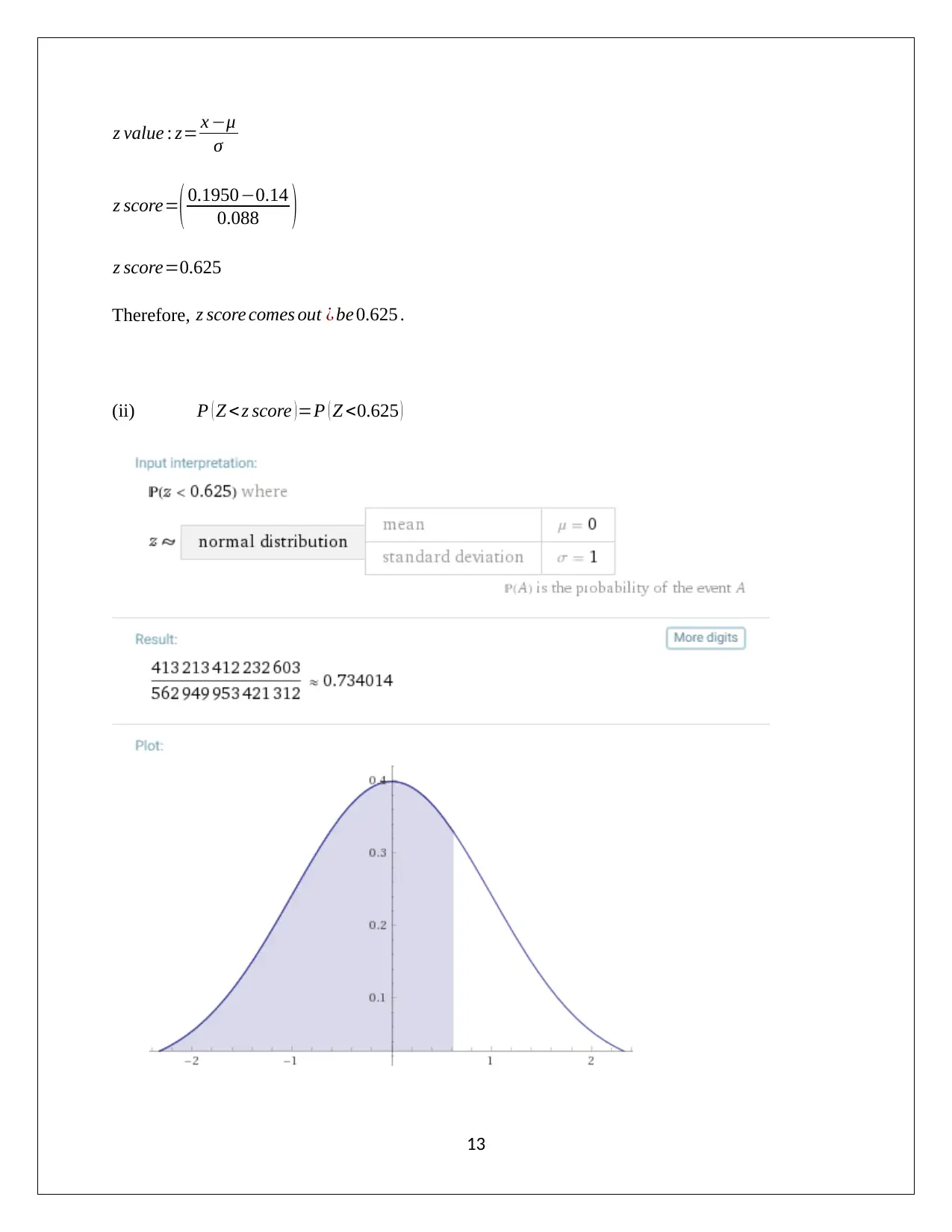
z value : z= x −μ
σ
z score=( 0.1950−0.14
0.088 )
z score=0.625
Therefore, z score comes out ¿ be 0.625 .
(ii) P ( Z < z score )=P ( Z <0.625 )
13

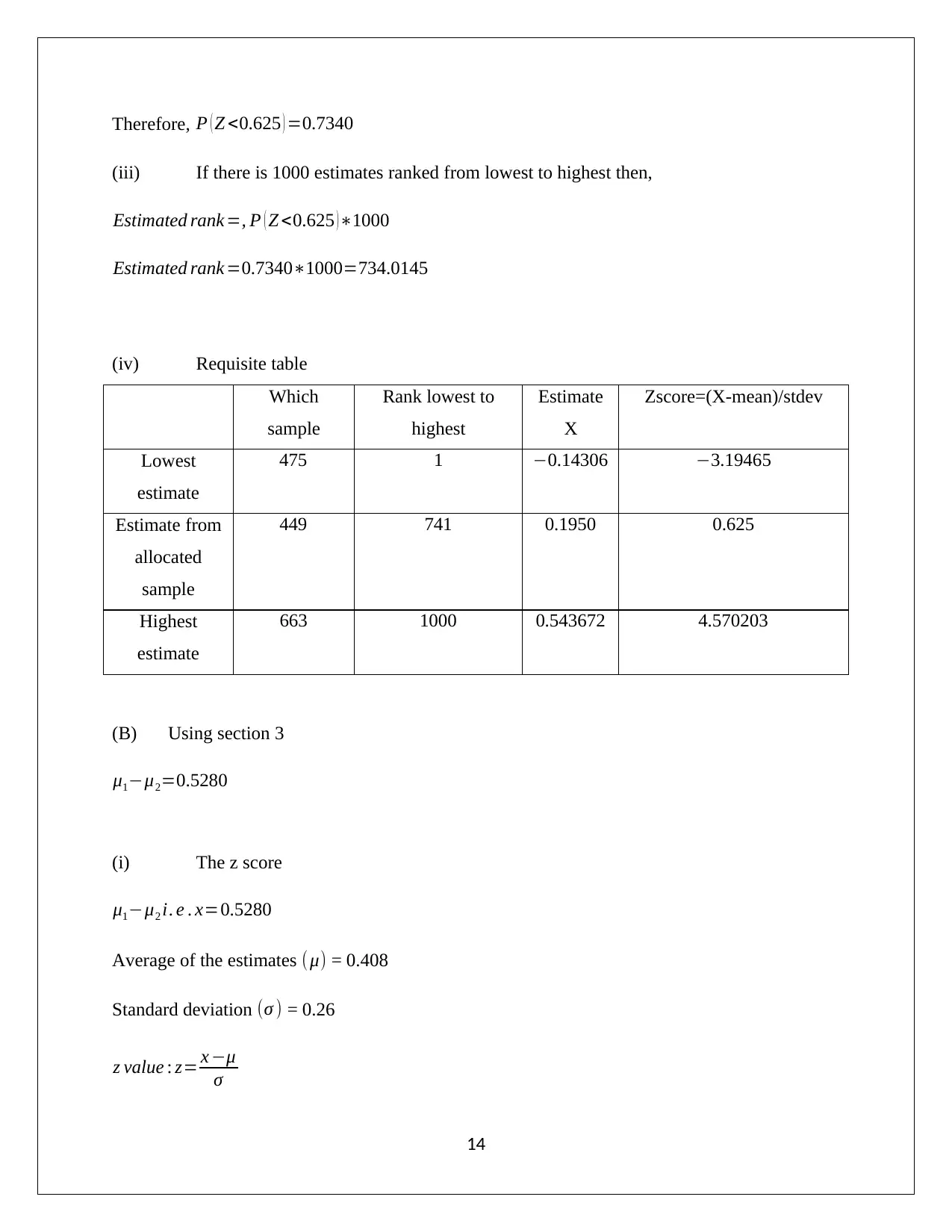
Therefore, P ( Z <0.625 ) =0.7340
(iii) If there is 1000 estimates ranked from lowest to highest then,
Estimated rank =, P ( Z <0.625 )∗1000
Estimated rank =0.7340∗1000=734.0145
(iv) Requisite table
Which
sample
Rank lowest to
highest
Estimate
X
Zscore=(X-mean)/stdev
Lowest
estimate
475 1 −0.14306 −3.19465
Estimate from
allocated
sample
449 741 0.1950 0.625
Highest
estimate
663 1000 0.543672 4.570203
(B) Using section 3
μ1−μ2=0.5280
(i) The z score
μ1−μ2 i. e . x=0.5280
Average of the estimates (μ) = 0.408
Standard deviation (σ ) = 0.26
z value : z= x −μ
σ
14

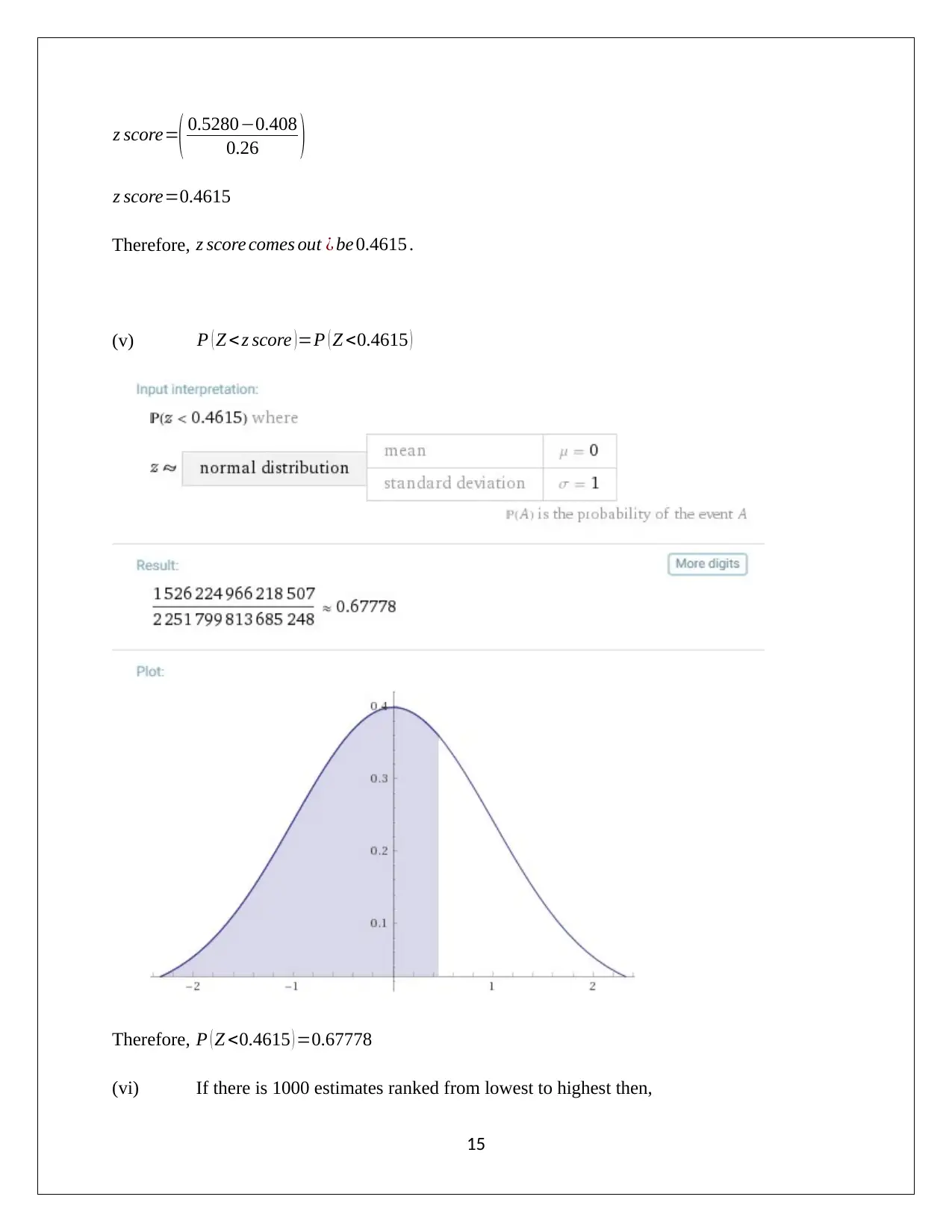
z score=( 0.5280−0.408
0.26 )
z score=0.4615
Therefore, z score comes out ¿ be 0.4615 .
(v) P ( Z < z score )=P ( Z <0.4615 )
Therefore, P ( Z <0.4615 ) =0.67778
(vi) If there is 1000 estimates ranked from lowest to highest then,
15

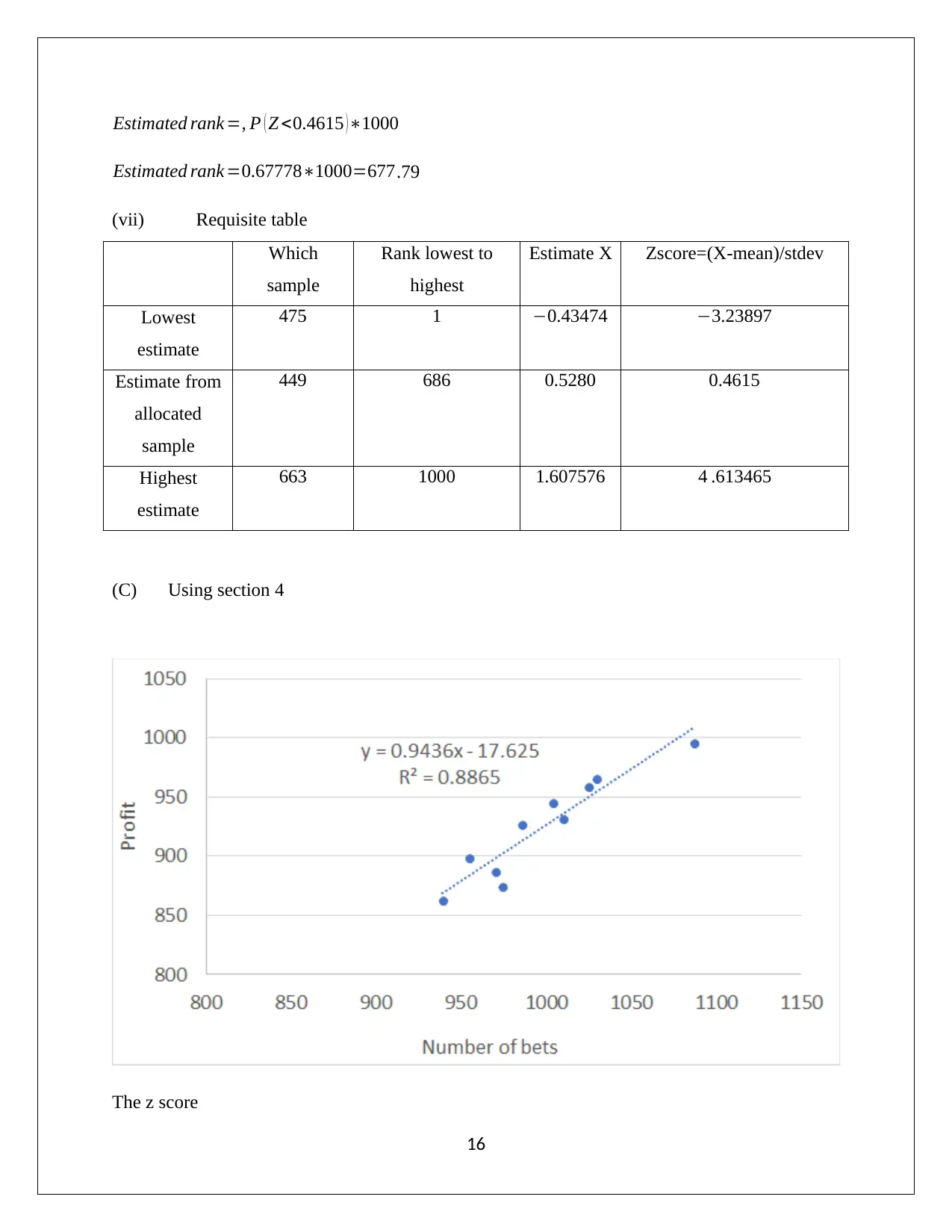
Estimated rank =, P ( Z <0.4615 )∗1000
Estimated rank =0.67778∗1000=677.79
(vii) Requisite table
Which
sample
Rank lowest to
highest
Estimate X Zscore=(X-mean)/stdev
Lowest
estimate
475 1 −0.43474 −3.23897
Estimate from
allocated
sample
449 686 0.5280 0.4615
Highest
estimate
663 1000 1.607576 4 .613465
(C) Using section 4
The z score
16

Slopeestimate=0.9436
Average of the estimates (μ) = 0.952
Standard deviation (σ ) = 0.237
z value : z= x −μ
σ
z score=( 0.9436−0.952
0.237 )
z score=−0.03544
Therefore, z score comes out ¿ be−0.03544 .
(viii) P ( Z < z score )=P ( Z <−0.03544 )
17

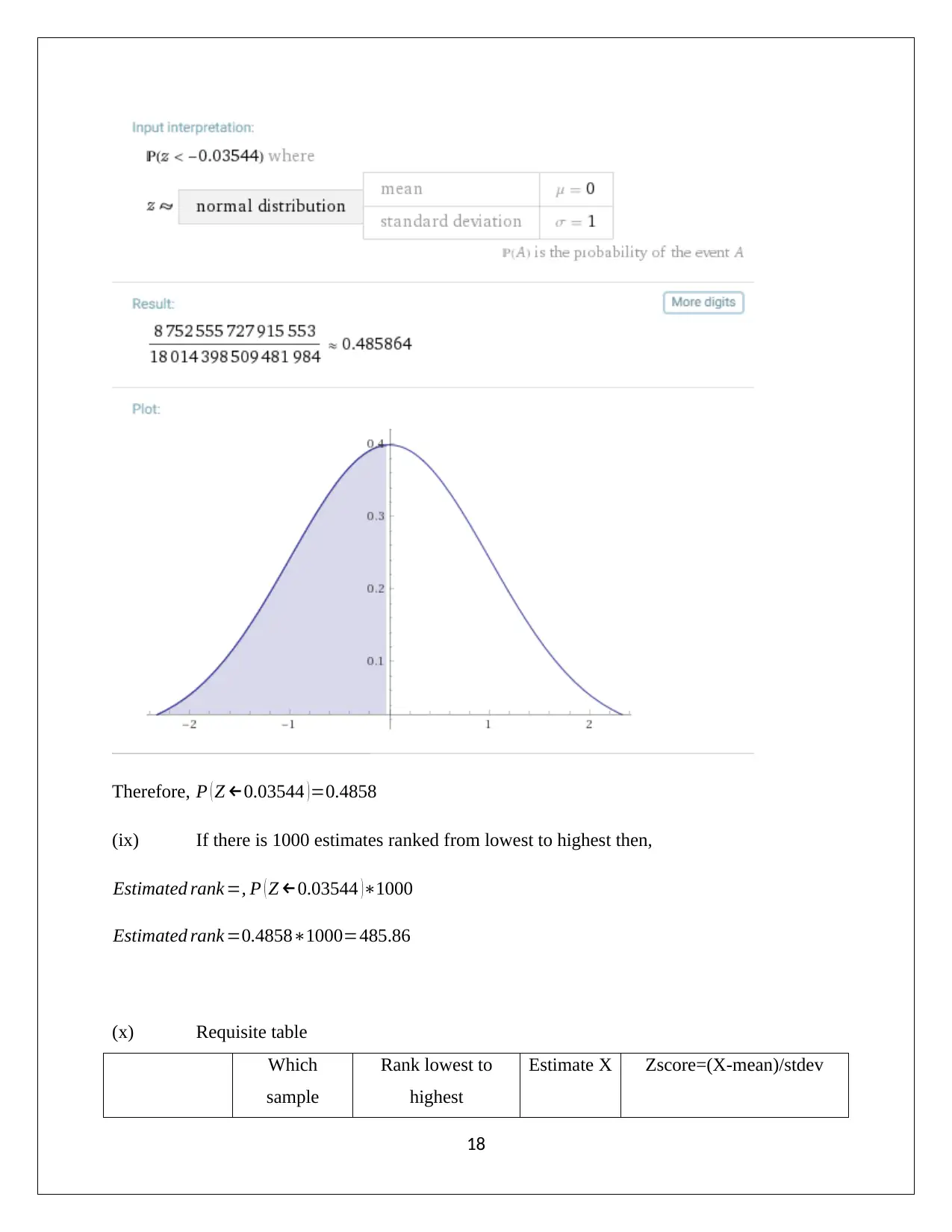
Therefore, P ( Z ←0.03544 )=0.4858
(ix) If there is 1000 estimates ranked from lowest to highest then,
Estimated rank =, P ( Z ←0.03544 )∗1000
Estimated rank =0.4858∗1000=485.86
(x) Requisite table
Which
sample
Rank lowest to
highest
Estimate X Zscore=(X-mean)/stdev
18

Lowest
estimate
141 1 −0.00348 −4.02937
Estimate from
allocated
sample
449 488 0.9436 −0.03544
Highest
estimate
398 1000 1.87172 3.876998
(D) It is apparent that actual rank of the allocated sample is 488 and the estimated rank in part
(A) and part (B) are significantly greater than the actual rank of the sample. However, for
part (C), the estimated rank of allocated sample comes out as 486 which is quite close to
the actual rank of 488.
(E) If the sampling distribution is the same, than comparison can be drawn even between
different datasets since the underlying properties tend to converge. This has been
exhibited here. Further, the sampling distribution plays a key role in hypothesis testing
and determination of the resultant p value. For the given case, the p value determination
has been done considering the normal distribution and if the distribution varies, then the
underlying process for determination of p value changes along with the value itself
(Flick, 2015).
19

References
Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research 3rd ed.
London: Sage Publications.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project. 4th ed. New York: Sage Publications.
Hair, J. F., Wolfinbarger, M., Money, A. H., Samouel, P., and Page, M. J. (2015) Essentials of
business research methods. 2nd ed. New York: Routledge.
Hillier, F. (2016) Introduction to Operations Research 6th ed. New York: McGraw Hill
Publications
20