Comprehensive Statistics Assignment: Data Analysis and Regression
VerifiedAdded on 2023/04/20
|11
|1566
|448
Homework Assignment
AI Summary
This statistics assignment solution provides a detailed analysis of data collection methods, focusing on the suitability of online surveys and stratified random sampling. It explores the relationship between preparation time and exam scores, identifying independent and dependent variables and discussing potential data collection issues. The solution includes frequency distributions and histograms to visualize data, scatter plots to assess correlations, and regression equations to model the relationship between variables. Furthermore, it covers hypothesis testing, standard error of estimate, and coefficient of determination in the context of multiple regression analysis, interpreting slope coefficients and determining statistical significance. This assignment, available on Desklib, offers valuable insights into statistical methods and their application in analyzing real-world data.

STATISTICS
Student ID
[Pick the date]
1
Student ID
[Pick the date]
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 1
a) Taking into consideration the nature of questions which are not difficult to understand, the
online survey method seems suitable for collection of data. Besides, conducting a face to face
survey may be difficult when a random sample has been selected because of the underlying
logistics. As a result, an online survey should be put in place and the link shared with the
sample respondents for collection of data (Hillier, 2016).
b) The sutiable sampling method deployed for sample selection would be stratified random
sampling. This has been chosen instead of simple random sampling in order to ensure that the
representation of key attributes matached with the population. These pivotal attributes could
be gender, country of origin besides educational background. These factors can impact the
data to be collected and hence attempt ought to be made to mirror the popualtion in these
regards (Flick, 2015).
c) For the given situation, the preparation time amount would be the independent variable as
with the marks scored as the dependent variable. This may be attributed to the fact that
scoring obtained in exams is a function of the preparation time. Further, both the variables are
numerical while the suitable mesurement scale is ratio as for both the variable, absolute zero
is defined (Eriksson and Kovalainen, 2015).
d) The issues in relation to data collection are highlighted as follows (Medhi, 2016).
The respondents may be only estimating the preparation time owing to which
accuracy is compromised. Also, the underlying time frame which ought to be used for
computation of preparation time seems to be missing which may lead to subjectivity
in interpretation.
The reporting of preparation time may be biased by the makrs scored. Students
scoring high marks may have a tendency to overestimate preparation time while those
scoring lower marks could underestimate preparation time.
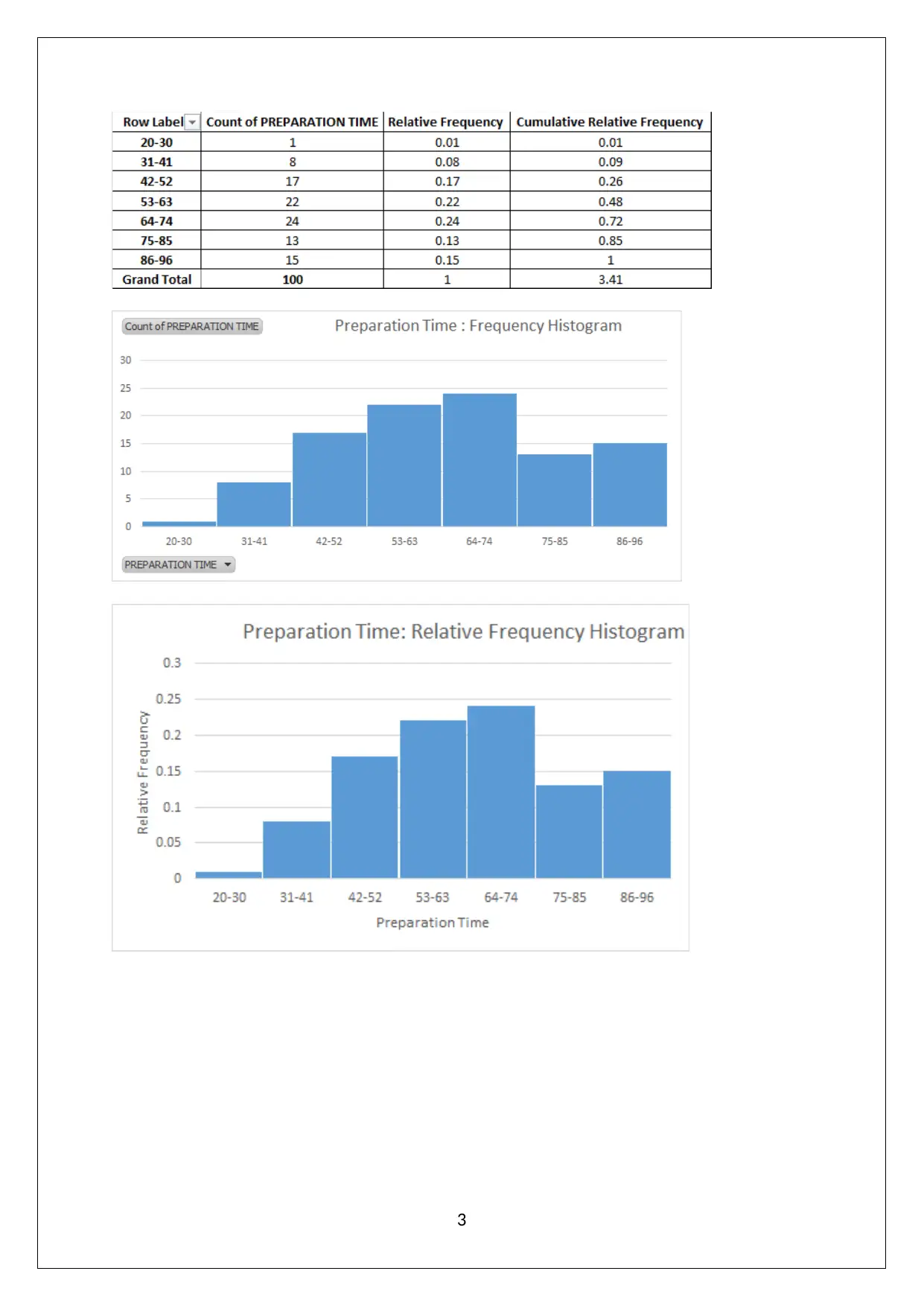
(e) Frequency distribution with 8 class intervals
Preparation time
2
a) Taking into consideration the nature of questions which are not difficult to understand, the
online survey method seems suitable for collection of data. Besides, conducting a face to face
survey may be difficult when a random sample has been selected because of the underlying
logistics. As a result, an online survey should be put in place and the link shared with the
sample respondents for collection of data (Hillier, 2016).
b) The sutiable sampling method deployed for sample selection would be stratified random
sampling. This has been chosen instead of simple random sampling in order to ensure that the
representation of key attributes matached with the population. These pivotal attributes could
be gender, country of origin besides educational background. These factors can impact the
data to be collected and hence attempt ought to be made to mirror the popualtion in these
regards (Flick, 2015).
c) For the given situation, the preparation time amount would be the independent variable as
with the marks scored as the dependent variable. This may be attributed to the fact that
scoring obtained in exams is a function of the preparation time. Further, both the variables are
numerical while the suitable mesurement scale is ratio as for both the variable, absolute zero
is defined (Eriksson and Kovalainen, 2015).
d) The issues in relation to data collection are highlighted as follows (Medhi, 2016).
The respondents may be only estimating the preparation time owing to which
accuracy is compromised. Also, the underlying time frame which ought to be used for
computation of preparation time seems to be missing which may lead to subjectivity
in interpretation.
The reporting of preparation time may be biased by the makrs scored. Students
scoring high marks may have a tendency to overestimate preparation time while those
scoring lower marks could underestimate preparation time.
(e) Frequency distribution with 8 class intervals
Preparation time
2
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Based on the above shown histograms, it can be said that distribution of preparation time
follows asymmetric distribution. Also, leftward skew is present (long leftward tail) in the
distribution which shows that data does not follow normal distribution.
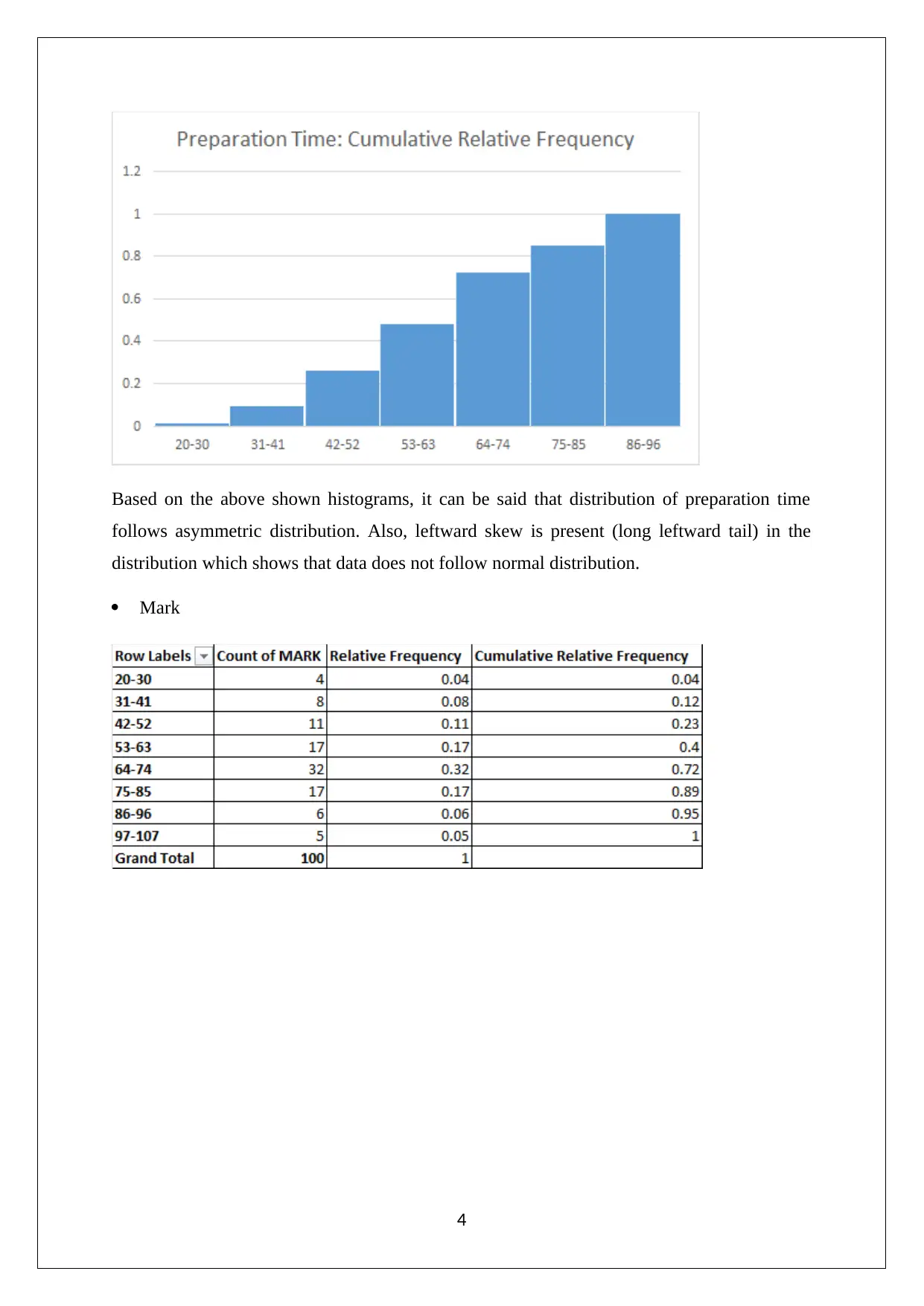
Mark
4
follows asymmetric distribution. Also, leftward skew is present (long leftward tail) in the
distribution which shows that data does not follow normal distribution.
Mark
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

5
Based on the above shown histograms, it can be said that distribution of mark follows
asymmetric distribution. Also, leftward skew is present (long leftward tail) in the distribution
which shows that data does not follow normal distribution.
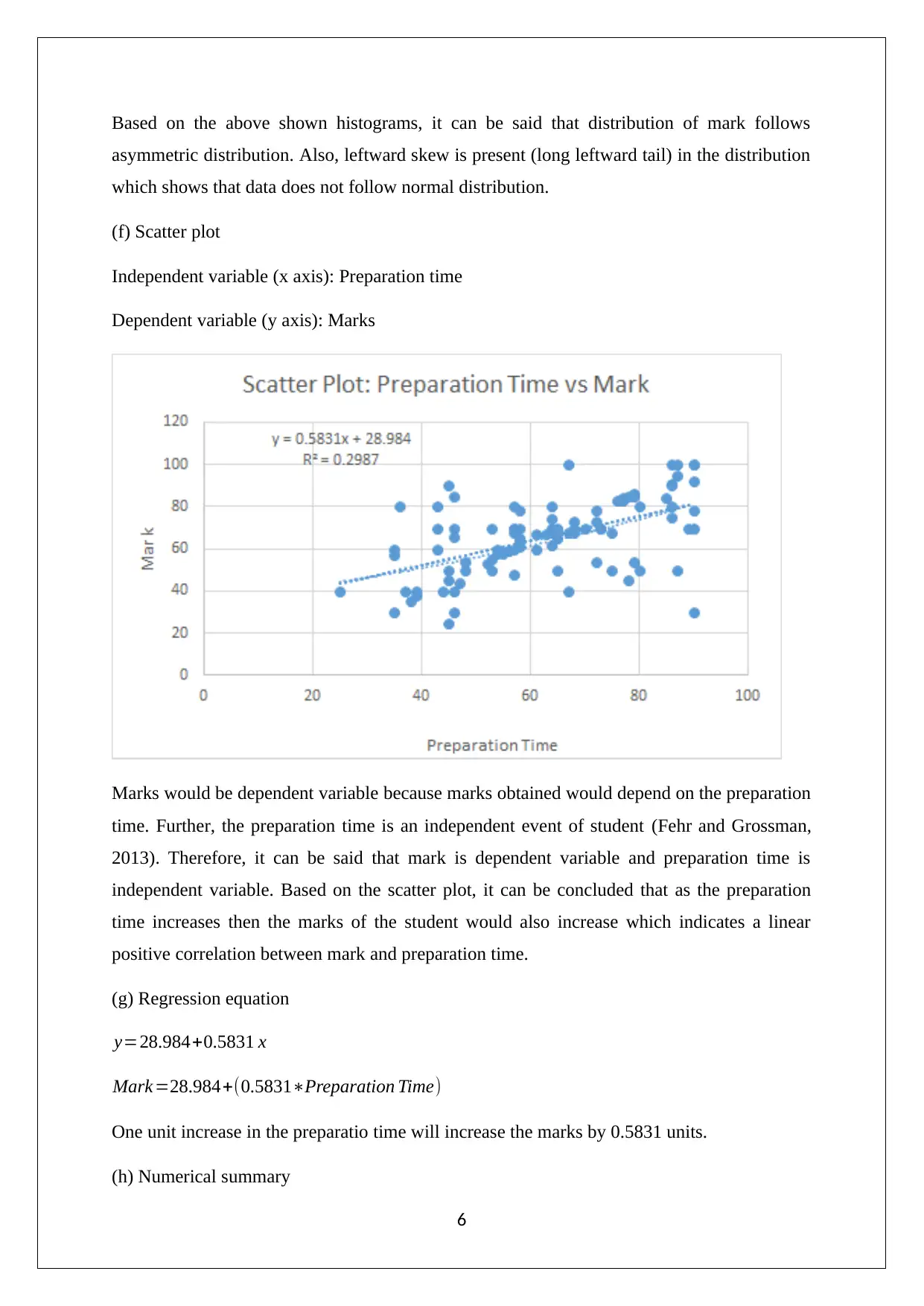
(f) Scatter plot
Independent variable (x axis): Preparation time
Dependent variable (y axis): Marks
Marks would be dependent variable because marks obtained would depend on the preparation
time. Further, the preparation time is an independent event of student (Fehr and Grossman,
2013). Therefore, it can be said that mark is dependent variable and preparation time is
independent variable. Based on the scatter plot, it can be concluded that as the preparation
time increases then the marks of the student would also increase which indicates a linear
positive correlation between mark and preparation time.
(g) Regression equation
y=28.984+0.5831 x
Mark=28.984+(0.5831∗Preparation Time)
One unit increase in the preparatio time will increase the marks by 0.5831 units.
(h) Numerical summary
6
asymmetric distribution. Also, leftward skew is present (long leftward tail) in the distribution
which shows that data does not follow normal distribution.
(f) Scatter plot
Independent variable (x axis): Preparation time
Dependent variable (y axis): Marks
Marks would be dependent variable because marks obtained would depend on the preparation
time. Further, the preparation time is an independent event of student (Fehr and Grossman,
2013). Therefore, it can be said that mark is dependent variable and preparation time is
independent variable. Based on the scatter plot, it can be concluded that as the preparation
time increases then the marks of the student would also increase which indicates a linear
positive correlation between mark and preparation time.
(g) Regression equation
y=28.984+0.5831 x
Mark=28.984+(0.5831∗Preparation Time)
One unit increase in the preparatio time will increase the marks by 0.5831 units.
(h) Numerical summary
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

(i) Correlation coefficient is considered as appropriate numerical measurement to
determine the strenght and direction of the linear association between the variables.
The correlation matrix is shown below.
7
determine the strenght and direction of the linear association between the variables.
The correlation matrix is shown below.
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
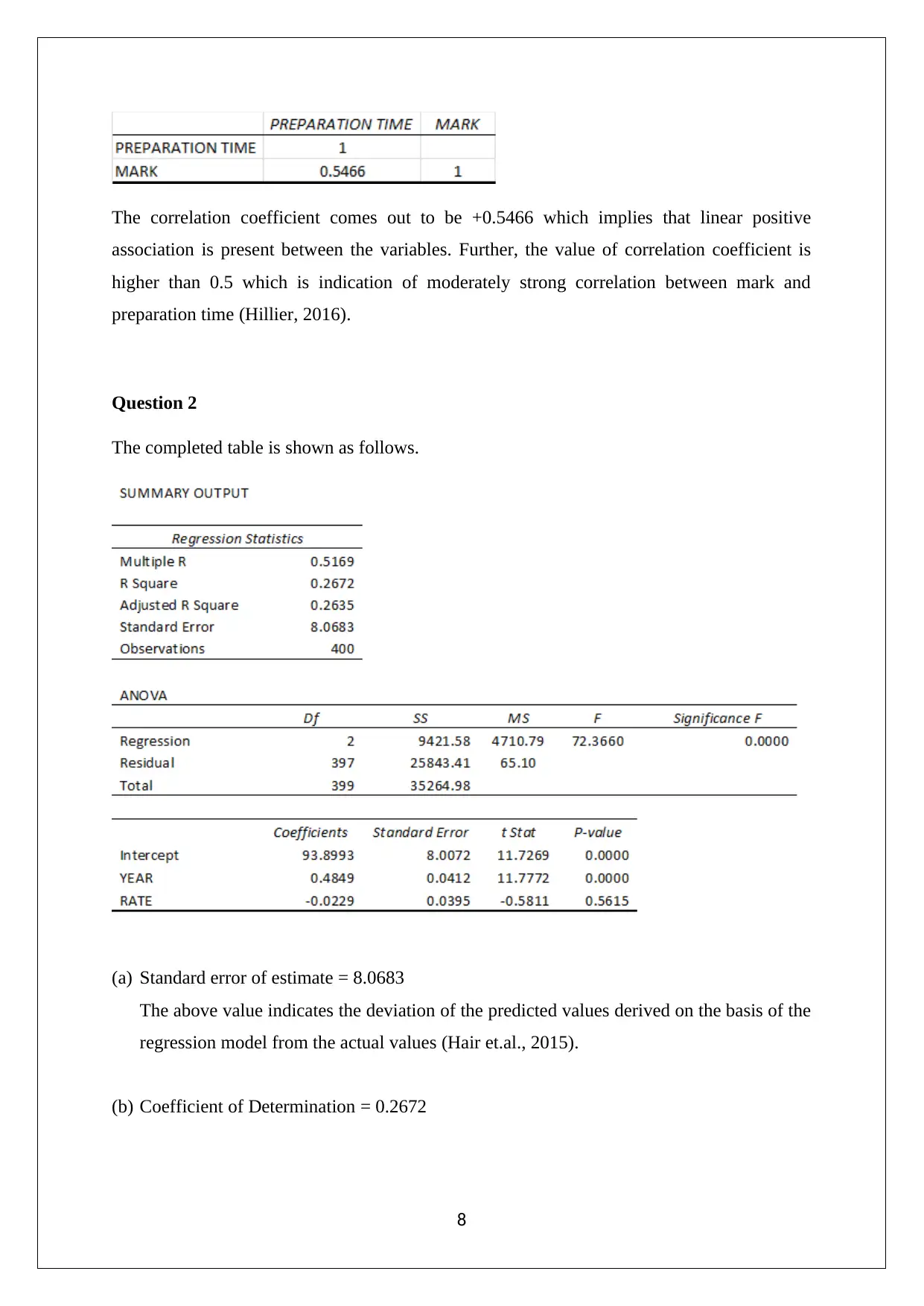
The correlation coefficient comes out to be +0.5466 which implies that linear positive
association is present between the variables. Further, the value of correlation coefficient is
higher than 0.5 which is indication of moderately strong correlation between mark and
preparation time (Hillier, 2016).
Question 2
The completed table is shown as follows.
(a) Standard error of estimate = 8.0683
The above value indicates the deviation of the predicted values derived on the basis of the
regression model from the actual values (Hair et.al., 2015).
(b) Coefficient of Determination = 0.2672
8
association is present between the variables. Further, the value of correlation coefficient is
higher than 0.5 which is indication of moderately strong correlation between mark and
preparation time (Hillier, 2016).
Question 2
The completed table is shown as follows.
(a) Standard error of estimate = 8.0683
The above value indicates the deviation of the predicted values derived on the basis of the
regression model from the actual values (Hair et.al., 2015).
(b) Coefficient of Determination = 0.2672
8

The above value indicates that 26.72% of the height of the son variations can be
accounted jointly by the independent variables considered in the above regression model
(Flick, 2015).
(c) The coefficient of determination is susceptible to the number of predictors. Hence, the
adjusted coefficient of determination is used which for the given case is 0.2635.
Considering the R2 and adjusted R2, it is apparent that the model represents a poor fit as
the underlying regression model has poor predictive power. Also, one of the independent
variable does not seem significant (Medhi, 2016).
(d) Hypothesis testing
Null and alternative hypotheses
Test statistic (F stat¿=( 4710.79
65.10 )=72.336
The p value (significance F) = 0.000
Significance level = 0.05
The p value is lower than significance level and hence, sufficient evidence is present to reject
the null hypothesis and to accept the alternative hypothesis (Shi and Tao, 2017). This implies
that at least one of the slope coefficients is not zero and hence, statistically significant.
Therefore, it can be concluded that the given multiple regression model is considered as
statistically significant.
(e) Interpretation of slope coefficients
9
accounted jointly by the independent variables considered in the above regression model
(Flick, 2015).
(c) The coefficient of determination is susceptible to the number of predictors. Hence, the
adjusted coefficient of determination is used which for the given case is 0.2635.
Considering the R2 and adjusted R2, it is apparent that the model represents a poor fit as
the underlying regression model has poor predictive power. Also, one of the independent
variable does not seem significant (Medhi, 2016).
(d) Hypothesis testing
Null and alternative hypotheses
Test statistic (F stat¿=( 4710.79
65.10 )=72.336
The p value (significance F) = 0.000
Significance level = 0.05
The p value is lower than significance level and hence, sufficient evidence is present to reject
the null hypothesis and to accept the alternative hypothesis (Shi and Tao, 2017). This implies
that at least one of the slope coefficients is not zero and hence, statistically significant.
Therefore, it can be concluded that the given multiple regression model is considered as
statistically significant.
(e) Interpretation of slope coefficients
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

father’s height (x1): When father’s height is increased by 1 unit then the respective son’s
height would also be increased by 0.4849 units. The sign of slope coefficient is positive
which indicates that direction of change is same.
Mother’s height (x2): When mother’s height is increased by 1 unit then the respective son’s
height would also be decreased by -0.0229 units. The sign of slope coefficient is negative
which indicates that direction of change in the variables is not same (Taylor and Cihon,
2017).
(f) Hypothesis testing (Father’s height and Son’s height)
Test statistic (t stat¿=11.77
The p value = 0.000
Significance level = 0.05
The p value is lower than significance level and hence, sufficient evidence is present to reject
the null hypothesis and to accept the alternative hypothesis (Koch, 2016). This implies that
the slope coefficients (father’s height) is statistically significant. Therefore, it can be
concluded that statistically significant correlation is present between father’s height and son’s
height.
(g) Hypothesis testing (Father’s height and Son’s height)
Test statistic (t stat ¿=−0.5811
The p value = 0.5615
Significance level = 0.05
The p value is higher than significance level and hence, insufficient evidence is present to
reject the null hypothesis and to accept the alternative hypothesis (Harmon, 2016). This
10
height would also be increased by 0.4849 units. The sign of slope coefficient is positive
which indicates that direction of change is same.
Mother’s height (x2): When mother’s height is increased by 1 unit then the respective son’s
height would also be decreased by -0.0229 units. The sign of slope coefficient is negative
which indicates that direction of change in the variables is not same (Taylor and Cihon,
2017).
(f) Hypothesis testing (Father’s height and Son’s height)
Test statistic (t stat¿=11.77
The p value = 0.000
Significance level = 0.05
The p value is lower than significance level and hence, sufficient evidence is present to reject
the null hypothesis and to accept the alternative hypothesis (Koch, 2016). This implies that
the slope coefficients (father’s height) is statistically significant. Therefore, it can be
concluded that statistically significant correlation is present between father’s height and son’s
height.
(g) Hypothesis testing (Father’s height and Son’s height)
Test statistic (t stat ¿=−0.5811
The p value = 0.5615
Significance level = 0.05
The p value is higher than significance level and hence, insufficient evidence is present to
reject the null hypothesis and to accept the alternative hypothesis (Harmon, 2016). This
10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

implies that the slope coefficients (mother’s height) is not statistically significant. Therefore,
it can be concluded that no statistically significant correlation is present between mother’s
height and son’s height. Thus, height of son is not associated with the height of the mother.
References
Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research. 3rd ed.
London: Sage Publications.
Fehr, F. H. and Grossman, G. (2013). An introduction to sets, probability and hypothesis
testing. 3rd ed. Ohio: Heath.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project. 4th ed. New York: Sage Publications.
Hair, J. F., Wolfinbarger, M., Money, A. H., Samouel, P., and Page, M. J. (2015) Essentials
of business research methods. 2nd ed. New York: Routledge.
Harmon, M. (2016) Hypothesis Testing in Excel - The Excel Statistical Master. 7th ed.
Florida: Mark Harmon.
Hillier, F. (2016) Introduction to Operations Research. 6th ed. New York: McGraw Hill
Publications.
Koch, K.R. (2016) Parameter Estimation and Hypothesis Testing in Linear Models. 2nd ed.
London: Springer Science & Business Media.
Medhi, J. (2016) Statistical Methods: An Introductory Text. 4th ed. Sydney: New Age
International.
Shi, N. Z. and Tao, J. (2017) Statistical Hypothesis Testing: Theory and Methods. 3rd ed.
Singapore: World Scientific.
Taylor, K. J. and Cihon, C. (2017) Statistical Techniques for Data Analysis. 2nd ed.
Melbourne: CRC Press.
11
it can be concluded that no statistically significant correlation is present between mother’s
height and son’s height. Thus, height of son is not associated with the height of the mother.
References
Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research. 3rd ed.
London: Sage Publications.
Fehr, F. H. and Grossman, G. (2013). An introduction to sets, probability and hypothesis
testing. 3rd ed. Ohio: Heath.
Flick, U. (2015) Introducing research methodology: A beginner's guide to doing a research
project. 4th ed. New York: Sage Publications.
Hair, J. F., Wolfinbarger, M., Money, A. H., Samouel, P., and Page, M. J. (2015) Essentials
of business research methods. 2nd ed. New York: Routledge.
Harmon, M. (2016) Hypothesis Testing in Excel - The Excel Statistical Master. 7th ed.
Florida: Mark Harmon.
Hillier, F. (2016) Introduction to Operations Research. 6th ed. New York: McGraw Hill
Publications.
Koch, K.R. (2016) Parameter Estimation and Hypothesis Testing in Linear Models. 2nd ed.
London: Springer Science & Business Media.
Medhi, J. (2016) Statistical Methods: An Introductory Text. 4th ed. Sydney: New Age
International.
Shi, N. Z. and Tao, J. (2017) Statistical Hypothesis Testing: Theory and Methods. 3rd ed.
Singapore: World Scientific.
Taylor, K. J. and Cihon, C. (2017) Statistical Techniques for Data Analysis. 2nd ed.
Melbourne: CRC Press.
11
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


