Exploring Statistical Data: Analysis, Plots, and Interpretation

This statistics assignment solution includes a box plot analysis identifying an outlier, which is then removed for subsequent calculations. The solution proceeds with a stem and leaf plot, followed by the calculation of the mean, median, mode, and standard deviation for the sample data. It verifie...Read More

STATISTICS
STUDENT NAME/ID
[Pick the date]

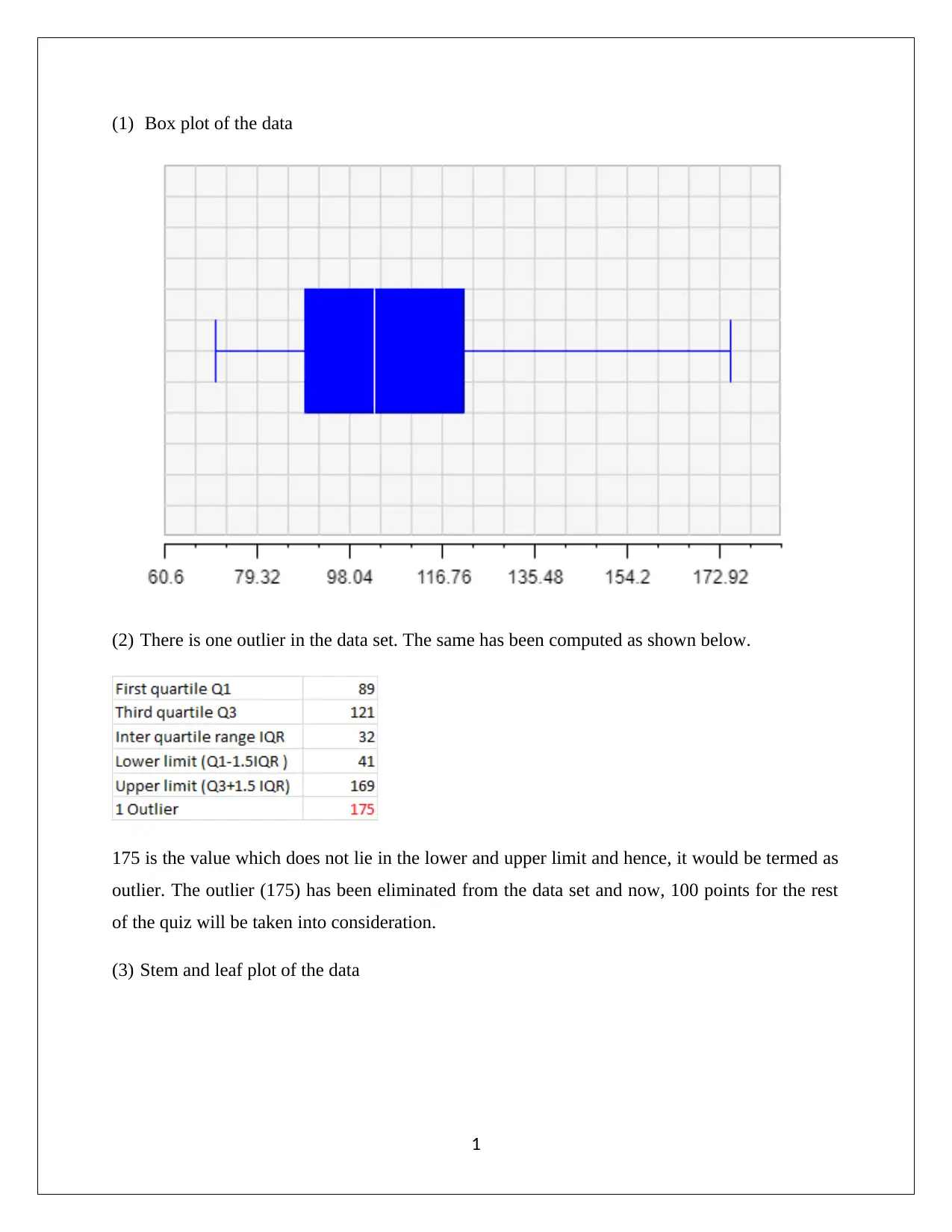
(1) Box plot of the data
(2) There is one outlier in the data set. The same has been computed as shown below.
175 is the value which does not lie in the lower and upper limit and hence, it would be termed as
outlier. The outlier (175) has been eliminated from the data set and now, 100 points for the rest
of the quiz will be taken into consideration.
(3) Stem and leaf plot of the data
1

(4) The mean of the sample data is 104.880.
(5) The median of the sample data is 102.500.
(6) The mode of the sample data is 88.
(7) The standard deviation of the sample is 18.206.
(8) The sample size is 100.
(9) The standard deviation of the population is 18.115.
(10) The given data set does follow the relationship of standard deviation of the sample and
standard deviation of the population. Hence, there is no need to re-derive the data set.
(11) Sorted data (ascending order) and median
2

3

It is apparent that sample size is an even number and therefore, the formula for even sample size
for median computation would be used as highlighted below.
Median={(n /2) thvalue+(( n/2)+1)th value ¿ }/ 2
Here , sample ¿ ¿ 100
Median={( 100
2 ) thvalue+(( 100
2 )+1)th value ¿ }/2={(50 th value+51 th value)}/2
Median=(102+103)/2=102.5
Yes, it can be seen that computed median value from sorted data agreed with the value computed
from excel function.
(12) 72nd percentile of the data = 117.28
It indicates that 72% of the data values are fall below than 117.28.
(13) Histogram with bin interval of 10 is highlighted below.
(14) Frequency table
4

(15) Relative frequency histogram
> 67.167 <=
77.167 > 77.167 <=
87.167 >87.167 <=
97.167 >97.167 <=
107.167 >107.167
<= 117.167 >117.167
<= 127.167 >127.167
<= 137.167 >137.167
<= 147.167
0
0.05
0.1
0.15
0.2
0.25
Relative frequency histogram
Range
Relative frequency
(16) Cumulative relative frequency histogram
5

> 67.167 <=
77.167 > 77.167 <=
87.167 >87.167 <=
97.167 >97.167 <=
107.167 >107.167 <=
117.167 >117.167 <=
127.167 >127.167 <=
137.167 >137.167 <=
147.167
0
0.2
0.4
0.6
0.8
1
1.2
Cumulative relative frequency histogram
Range
Cumulative relative frequency
(17) Sample size of likely voters when margin of error =1%
Sample siz e= z∗√ ¿
Sample ¿ ( 1.96∗
√ 0.5∗1000∗0.5
1 % )
2
=96040
(18) Distribution of ‘A’ has largest mean.
 The mean of distribution of A has ‘about the same’ the median.
 The mean of distribution of B has “less than” the median.
 The distribution of ‘A’ has the highest median value.
 The distribution of B has ‘a left skew.’
(19) Bar chart of popular vote
6

Woodrow Wilson
Theodore Roosevelt
William Taft
Eugene Debs
0 5 10 15 20 25 30 35 40 45
Bar Chart
% popular votes
Candidate
Pie chart of electoral vote
Woodrow Wilson ; 435
Theodore Roosevelt ; 88
William Taft ; 8
Pie Chart
7