Statistics Study Material with Solved Assignments and Examples - Desklib

This study material covers various topics in Statistics including contingency tables, non-normal distribution, experimental studies, binomial distribution, and more. It includes solved examples and assignments. The material is suitable for students pursuing Statistics courses in colleges and universities.

STATISTICS
Student Name/Id
[Pick the date]

1
Question 1
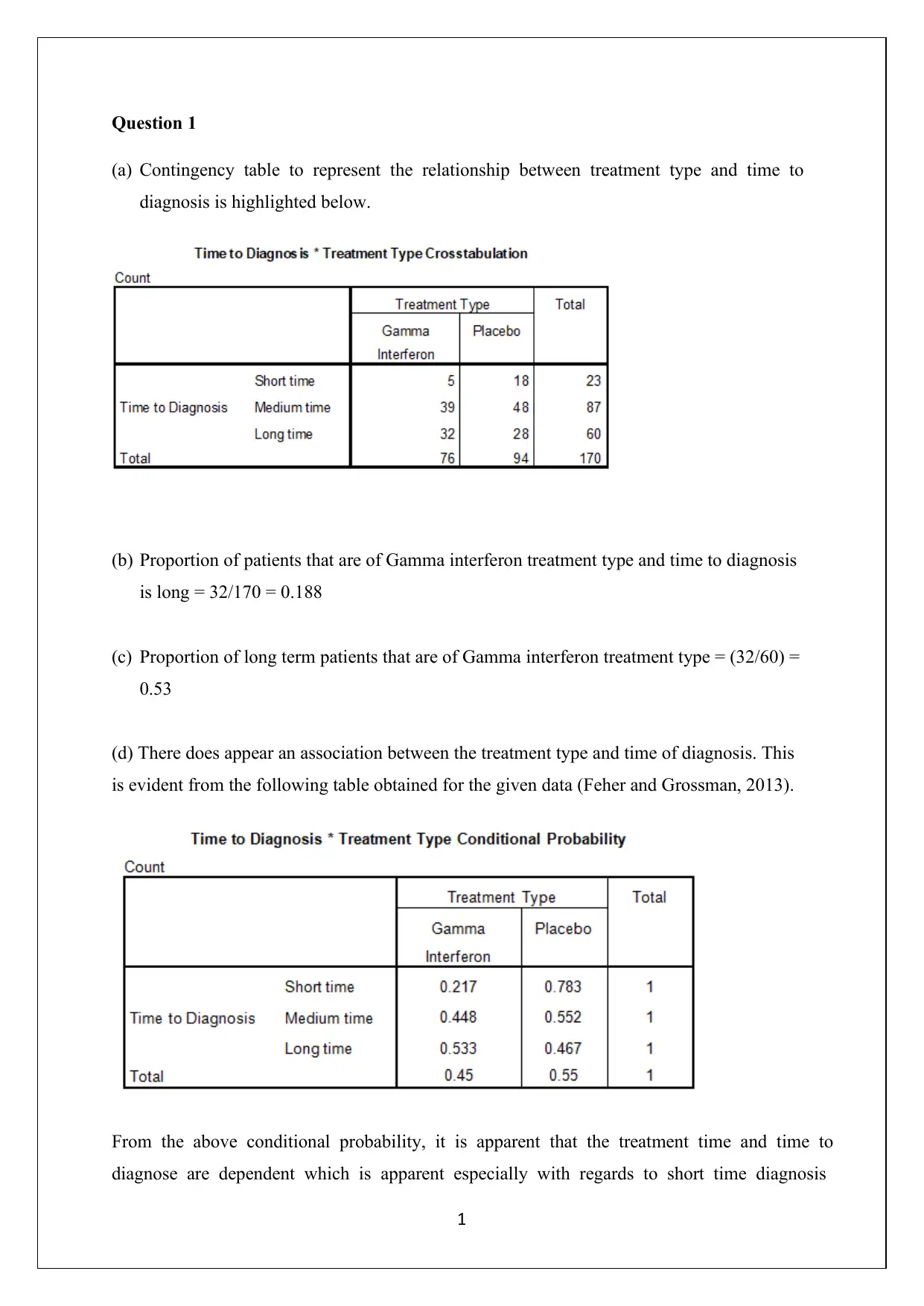
(a) Contingency table to represent the relationship between treatment type and time to
diagnosis is highlighted below.
(b) Proportion of patients that are of Gamma interferon treatment type and time to diagnosis
is long = 32/170 = 0.188
(c) Proportion of long term patients that are of Gamma interferon treatment type = (32/60) =
0.53
(d) There does appear an association between the treatment type and time of diagnosis. This
is evident from the following table obtained for the given data (Feher and Grossman, 2013).
From the above conditional probability, it is apparent that the treatment time and time to
diagnose are dependent which is apparent especially with regards to short time diagnosis

2
cases. A vast majority of these belong to placebo treatment thus lending credibility to the
conclusion that for placebo treatment, short time diagnosis seems more probable.
Question 2
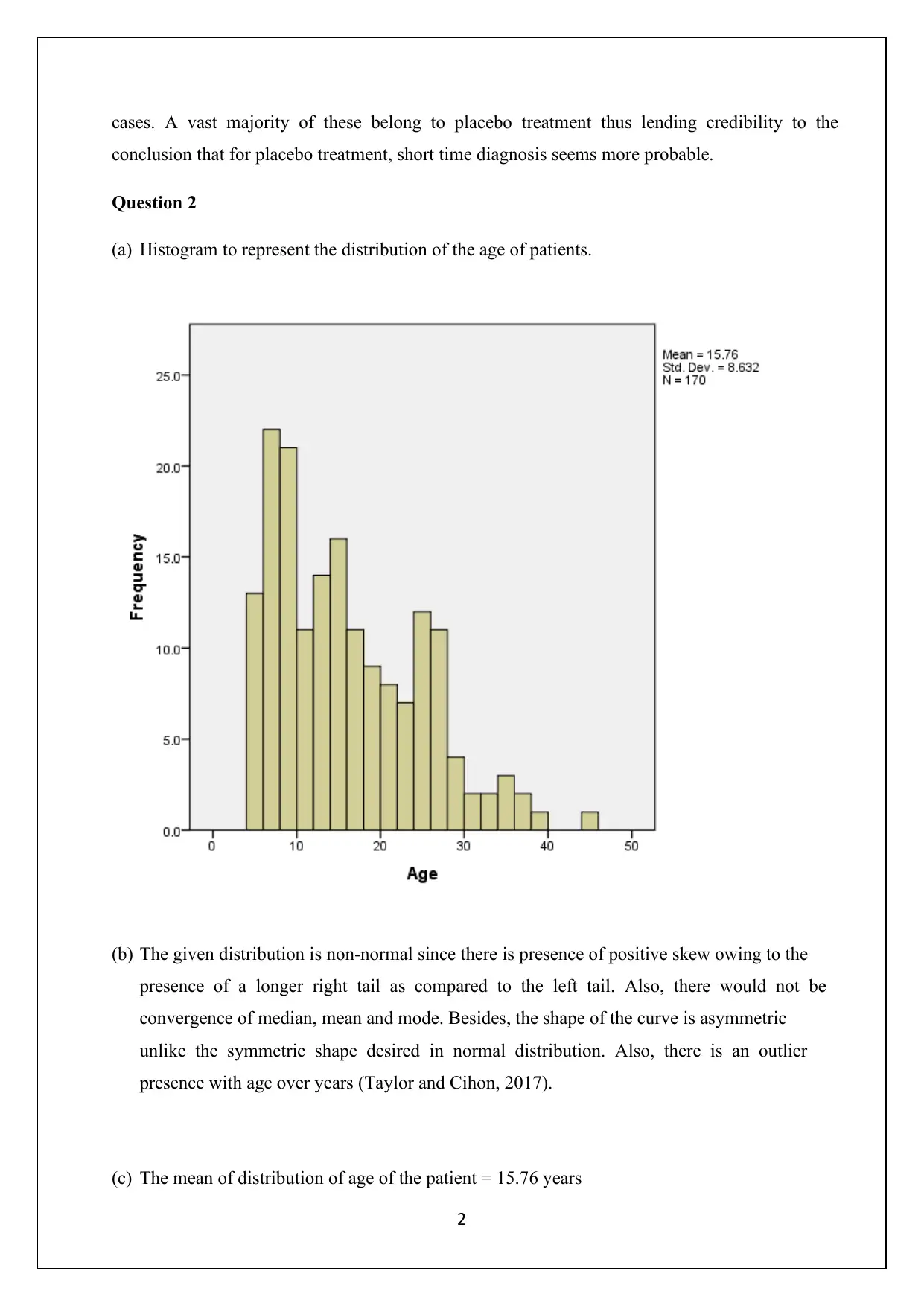
(a) Histogram to represent the distribution of the age of patients.
(b) The given distribution is non-normal since there is presence of positive skew owing to the
presence of a longer right tail as compared to the left tail. Also, there would not be
convergence of median, mean and mode. Besides, the shape of the curve is asymmetric
unlike the symmetric shape desired in normal distribution. Also, there is an outlier
presence with age over years (Taylor and Cihon, 2017).
(c) The mean of distribution of age of the patient = 15.76 years

3
Standard deviation of age of the patients = 8.632 years
(d) Median of distribution of age of the patient = 14.00 years
IQR of distribution of age of the patient = 14.00 years
Considering the skewed nature of the data, mean would not be a fair representative of the
central tendency as it could be influenced by the presence of outliers. As a result, median
would a suitable measure of central tendency especially taking into consideration that median
is not influenced by extreme value. Owing to skewed data, standard deviation is not a
suitable choice for measurement of dispersion since it would be influenced by incorrect
mean. As a result, IQR is the suitable option for measuring dispersion without being
influenced by extreme values or outliers (Medhi, 2016).
Question 3
a) The given study is experimental study since the independent variable is under the control
of the researcher and by administering various treatments, the researcher is recording the
results obtained in various groups so as to analyse the impact of each of the treatments
(fertilizer) on the yield of corn.
b) The response variable is the yield of corn (in kgs). The factor variable is the type of
fertilizer and there are three levels to the same namely A, B and C depending upon the
difference in ratio of potassium and nitrogen peroxide. The experimental unit correspond to
each of 150 plots used for this experiment.
c) One of principles is to have a control which has not been done since there is no
experimental unit without application of any fertiliser. However, the second principle of
randomisation has been adhered to since the factor treatment to experiments units is random
in nature. The third principle of replication is adhered since every treatment is extended to 50
plots and not one. No concrete measures seem to be in place for blcking.
d) A confounding variable is one which tends to influence both the dependent and
independent variables in a given study and hence can lead to a spurious relationship between
the dependent and independent variables. One of the confounding variables would be soil

4
type which would impact the suitable type of fertiliser based on the underlying deficiency of
minerals in soil. Also, the soil would determine the productivity of corn. Thus, a given factor
which is superior in the given experiment may fail elsewhere owing to difference in soil
composition.
Question 4
a) The variable of interest is the weight of infant born while the unit of measurement is kg.
b) The corresponding value of z from the z table which would result in a probability value of
0.01 is -2.326 (Medhi, 2016)
Also, we know that Z = (X- Mean)/Standard Deviation
In the given case, mean = 2.9 kg, standard deviation = 0.45 kg
Hence, -2.326 = (X-2.9)/0.45
Solving the above, we get X = 1.85 kg
Thus, 99% of the infants would have a weight in excess of 1.85 kg.
c) Percentage of new born babies weighted between 1.8 kg and 4.0 kg
( ) ( ) ( )
Therefore, there is a 98.54% of new born babies weighted between 1.8 kg and 4.0 kg.
(d) Probability that new born babies weighted less than 3.5 kg.
( ) ( ) ( )
Now,
Number of babies weighing less than 3.5 kg when there are15000 babies born =

5
Question 5
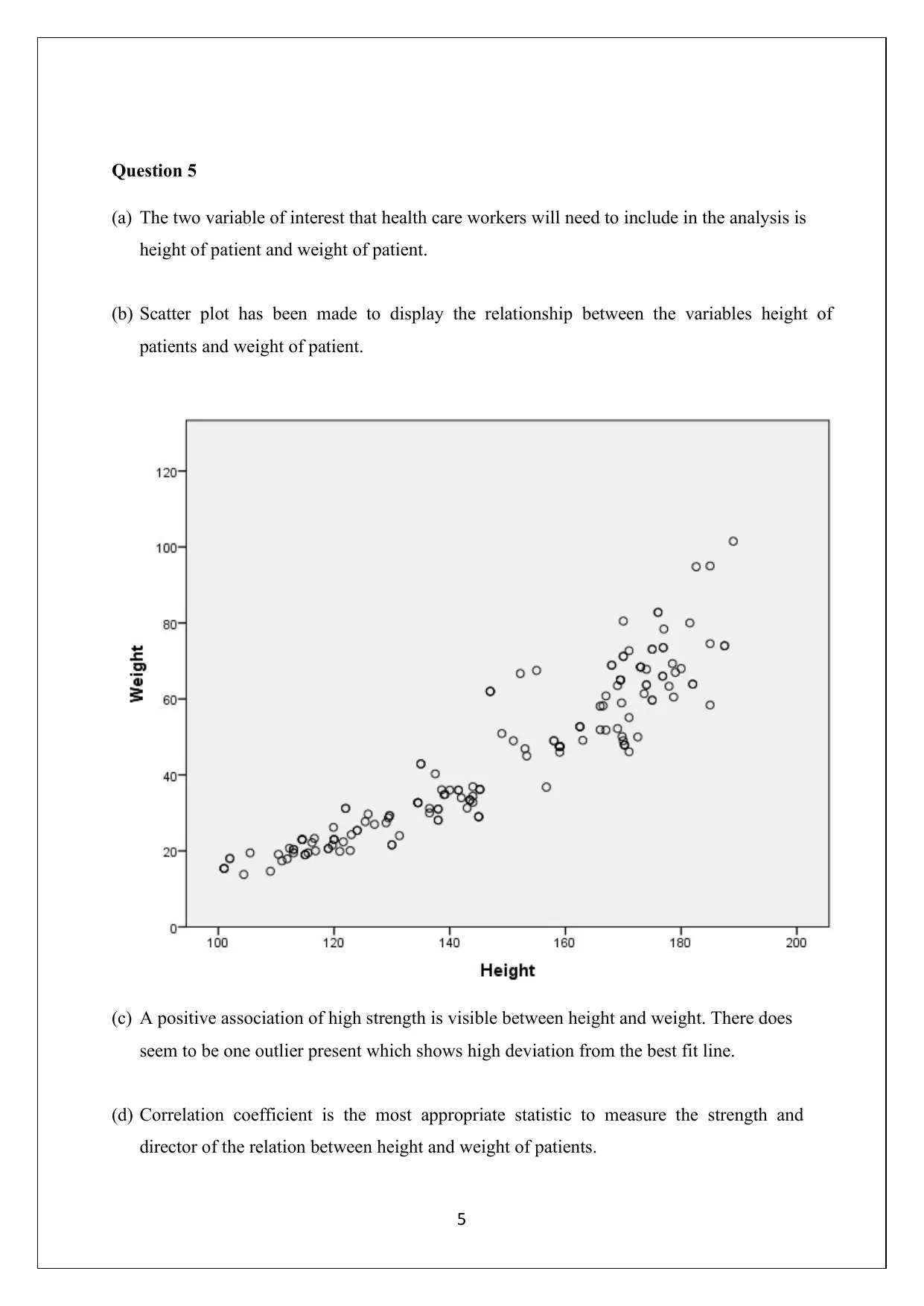
(a) The two variable of interest that health care workers will need to include in the analysis is
height of patient and weight of patient.
(b) Scatter plot has been made to display the relationship between the variables height of
patients and weight of patient.
(c) A positive association of high strength is visible between height and weight. There does
seem to be one outlier present which shows high deviation from the best fit line.
(d) Correlation coefficient is the most appropriate statistic to measure the strength and
director of the relation between height and weight of patients.

6
The value of correlation comes out to ne 0.922.
The value of correlation is close to 1 which indicates that height and weight of patient are
having strong positive relationship.
(e) Regression model
Regression equation

7
( )
(f) Weight of patient =?
Height of patient = 200 cm
( )
( )
(g) The R2 value is 0.85 which implies that 85% of the variation seen in weight can be
explained by corresponding changes in height of patients.
Question 6
a) The variable of interest in the showing of undesirable side effects by patients.
b) The appropriate model to represent the given variable would be binomial distribution since
there are only two outcomes possible with regards to side effects. The various parameters of
this model are as follows.
Number of trial= 10
Probability of patient getting side effect = 0.15
Probability of patient not getting side effect = 1-0.15 = 0.85
c) The various conditions for a binomial distribution are listed below.
 The underlying experiment should be based on n trials which are identical in nature.
 For each of these n trials, only two outputs i.e. success and failure possible.
 For each trial, there is no change in probability of success.
 Each of the n trials are independent
The given study fulfils the above conditions as exhibited below.

8
 For all the 10 patients, everything would be identical.
 For each of the patients, side effect may occur or may not occur.
 The probability of side effect appearing is 0.15 for each of the 10 patients.
 The outcome of one patient is not connected to the other.
d) Mean = np = 10*0.15 – 1.5 patients
Standard Deviation = √np(1-p) = (10*0.15*(1-0.15))0.5 = 1.13 patients
e) Requisite probability ( ) ( ) ( ) ( )
Formula for binomial distribution
( ) ( )
Where,
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )

9
f) In the given case, the binomial distribution needs to be approximated as normal
distribution. In order to ensure the same, the following two thumb rules need to be adhered to
(Feher and Grossman, 2013).
1) np >5 and also n(1-p)>5
2) np(1-p)>9
In the given case, np = 150*0.15 = 22.5
N(1-p) = 150*0.85 = 127.5
Np(1-p) = 150*0.15*0.85 = 19.13
It is apparent that the given approximation to normal distribution satisfies the various thumb
rules.
Mean of normal distribution = np = 150*0.15 = 22.5
Standard deviation of normal distribution = √np(1-p) = √150*0.15*0.85 = 4.37
Z statistics = (30-22.5)/4.37 = 1.715
P(X≥30) = P(Z≥1.715)
As per z table, P(Z<1.715) = 0.9568
Hence, requisite probability = 1-0.9568 = 0.043

10
References
Fehr, F. H. and Grossman, G. (2013) An introduction to sets, probability and hypothesis
testing. 3rd ed. Ohio: Heath.
Medhi, J. (2016) Statistical Methods: An Introductory Text. 4th ed. Sydney: New Age
International.
Taylor, K. J. and Cihon, C. (2017) Statistical Techniques for Data Analysis. 2nd ed.
Melbourne: CRC Press.