Symmetry and Normality of the Tovee Data

STATISTICS
Question One
Part a
Normality can be defined as the property of a dataset or variables in a dataset to be
modelled by a normal distribution (Barbara & Susan, 2014). Symmetry is closely related to
normality and it refers to the property of the distribution of a dataset or variables in a dataset to
be balanced evenly (or almost evenly) on both sides about the mean (O'Neil & Schutt, 2013;
Vicenc, 2017).
Here we evaluate the symmetry and normality of three variables from the Tovee Data;
VAS_choice for the Visual Analogue Scale, BMI for the Body Mass Index and WHR for the
Weight-Hip Ratio. The visual analogue scale refers to a measurement scale applied in measuring
when the subject is thought to lie across a wide range of values (Reips & Frederik, 2008).
Normality and Symmetry of VAS_choice
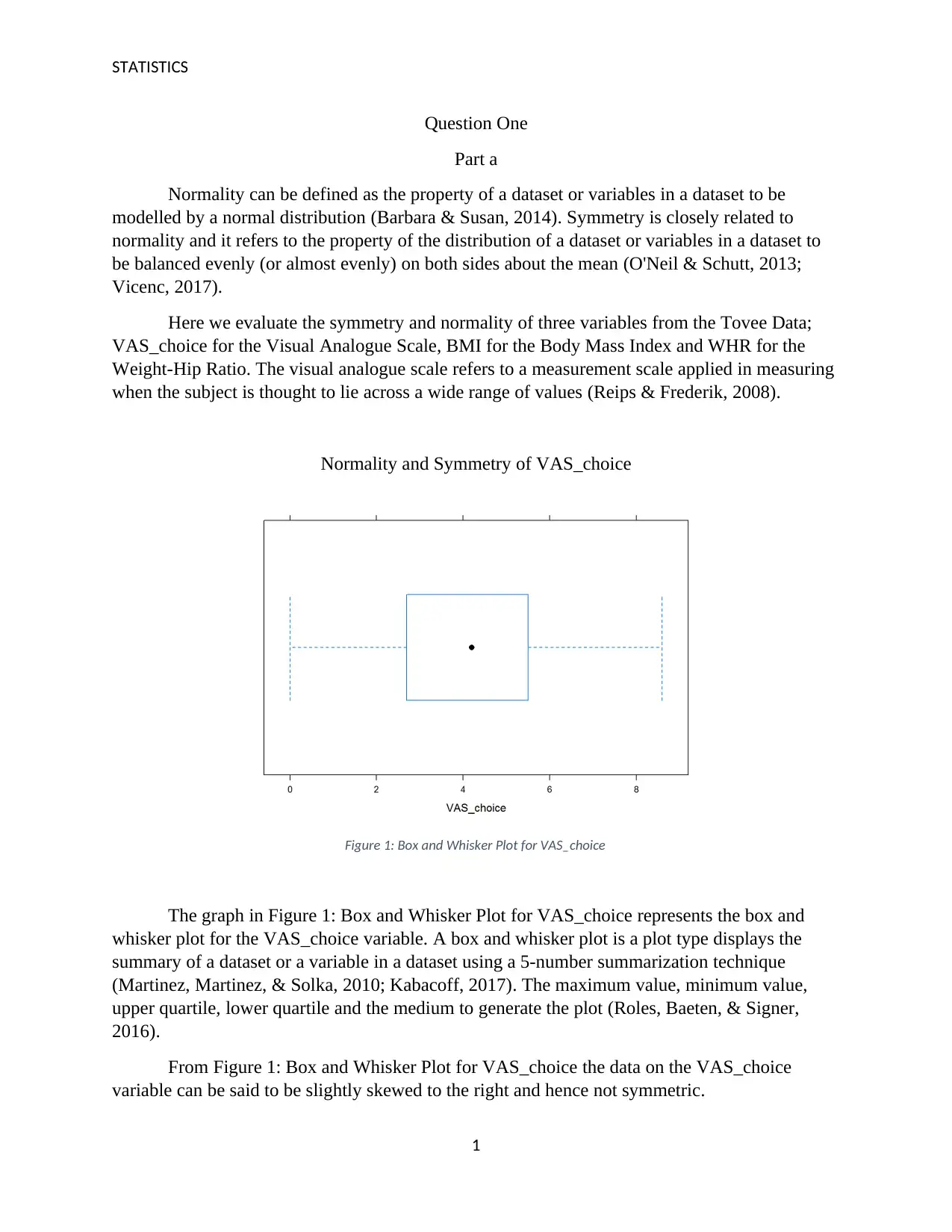
Figure 1: Box and Whisker Plot for VAS_choice
The graph in Figure 1: Box and Whisker Plot for VAS_choice represents the box and
whisker plot for the VAS_choice variable. A box and whisker plot is a plot type displays the
summary of a dataset or a variable in a dataset using a 5-number summarization technique
(Martinez, Martinez, & Solka, 2010; Kabacoff, 2017). The maximum value, minimum value,
upper quartile, lower quartile and the medium to generate the plot (Roles, Baeten, & Signer,
2016).
From Figure 1: Box and Whisker Plot for VAS_choice the data on the VAS_choice
variable can be said to be slightly skewed to the right and hence not symmetric.
1

STATISTICS
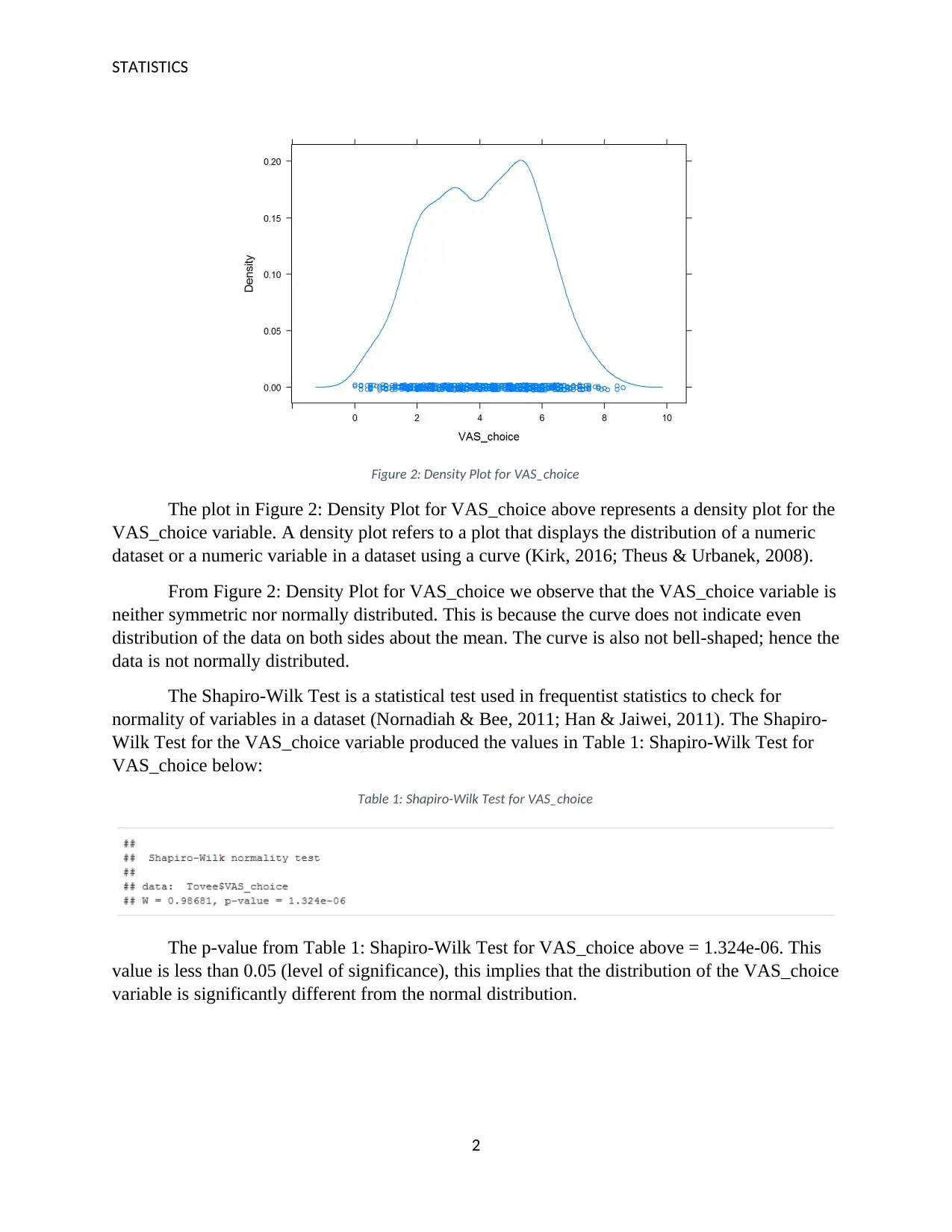
Figure 2: Density Plot for VAS_choice
The plot in Figure 2: Density Plot for VAS_choice above represents a density plot for the
VAS_choice variable. A density plot refers to a plot that displays the distribution of a numeric
dataset or a numeric variable in a dataset using a curve (Kirk, 2016; Theus & Urbanek, 2008).
From Figure 2: Density Plot for VAS_choice we observe that the VAS_choice variable is
neither symmetric nor normally distributed. This is because the curve does not indicate even
distribution of the data on both sides about the mean. The curve is also not bell-shaped; hence the
data is not normally distributed.
The Shapiro-Wilk Test is a statistical test used in frequentist statistics to check for
normality of variables in a dataset (Nornadiah & Bee, 2011; Han & Jaiwei, 2011). The Shapiro-
Wilk Test for the VAS_choice variable produced the values in Table 1: Shapiro-Wilk Test for
VAS_choice below:
Table 1: Shapiro-Wilk Test for VAS_choice
The p-value from Table 1: Shapiro-Wilk Test for VAS_choice above = 1.324e-06. This
value is less than 0.05 (level of significance), this implies that the distribution of the VAS_choice
variable is significantly different from the normal distribution.
2

STATISTICS
Normality and Symmetry of BMI
Figure 3: Box and Whisker Plot for BMI
From Figure 3: Box and Whisker Plot for BMI the data on the BMI variable can be said
to be almost symmetric.
Figure 4: Density Plot for BMI
From Figure 4: Density Plot for BMI we observe that the BMI variable is neither
symmetric nor normally distributed. This is because the curve does not indicate even distribution
of the data on both sides about the mean. The curve is also not bell-shaped; hence the data is not
normally distributed.
3

STATISTICS
The Shapiro-Wilk Test for the BMI variable produced the values in Table 2: Shapiro-
Wilk Test for BMI below:
Table 2: Shapiro-Wilk Test for BMI
The p-value from Table 2: Shapiro-Wilk Test for BMI above = 7.334e-15. This value is
less than 0.05 (level of significance), this implies that the distribution of the BMI variable is
significantly different from the normal distribution.
Normality and Symmetry of WHR
Figure 5: Box and Whisker Plot for WHR
From Figure 5: Box and Whisker Plot for WHR the data on the WHR variable can be
said to be skewed to the left and hence not symmetric.
4

STATISTICS
Figure 6: Density Plot for WHR
From Figure 6: Density Plot for WHR we observe that the WHR variable is neither
symmetric nor normally distributed. This is because the curve does not indicate even distribution
of the data on both sides about the mean. The curve is also not bell-shaped; hence the data is not
normally distributed.
The Shapiro-Wilk Test for the BMI variable produced the values in Table 2: Shapiro-
Wilk Test for BMI below:
Table 3: Shapiro-Wilk Test for WHR
The p-value from Table 3: Shapiro-Wilk Test for WHR above < 2.2e-16. This value is
less than 0.05 (level of significance), this implies that the distribution of the WHR variable is
significantly different from the normal distribution.
5

STATISTICS
Part b
The Box-Cox transformation is a transformation technique in statistics that transforms
data variables that have non-normal distributions into normally distributed variables (Ulf-
Dietrich & Uwe, 2014). The Box-Cox transformation is a power based transformation method
where the data points of the data variable that has non-normal distribution are raised to a given
power to achieve normality (Witten, 2011).
The Box-Cox transformation is suitable for the transformation of the BMI variables from
a non-normal variable to a normal variable.
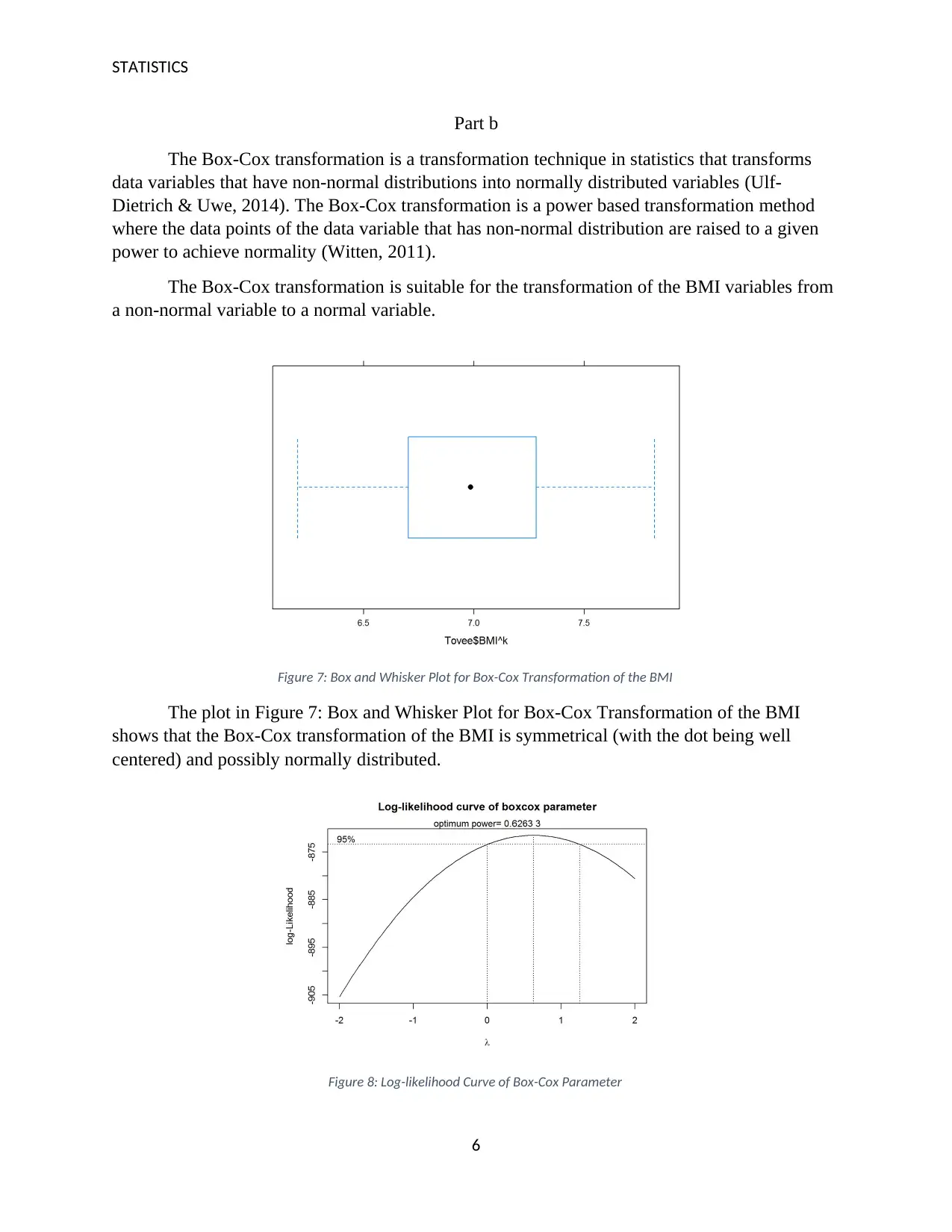
Figure 7: Box and Whisker Plot for Box-Cox Transformation of the BMI
The plot in Figure 7: Box and Whisker Plot for Box-Cox Transformation of the BMI
shows that the Box-Cox transformation of the BMI is symmetrical (with the dot being well
centered) and possibly normally distributed.
Figure 8: Log-likelihood Curve of Box-Cox Parameter
6

STATISTICS
From the plot in Figure 8: Log-likelihood Curve of Box-Cox Parameter above, we
observe a bell-shaped curve for log-likelihood. This implies that the Box-Cox transformation of
the BMI variable has resulted in normally distributed data points. The optimum power for the
Box-Cox transformation of the BMI variable has also been given as 0.62633.
Part c
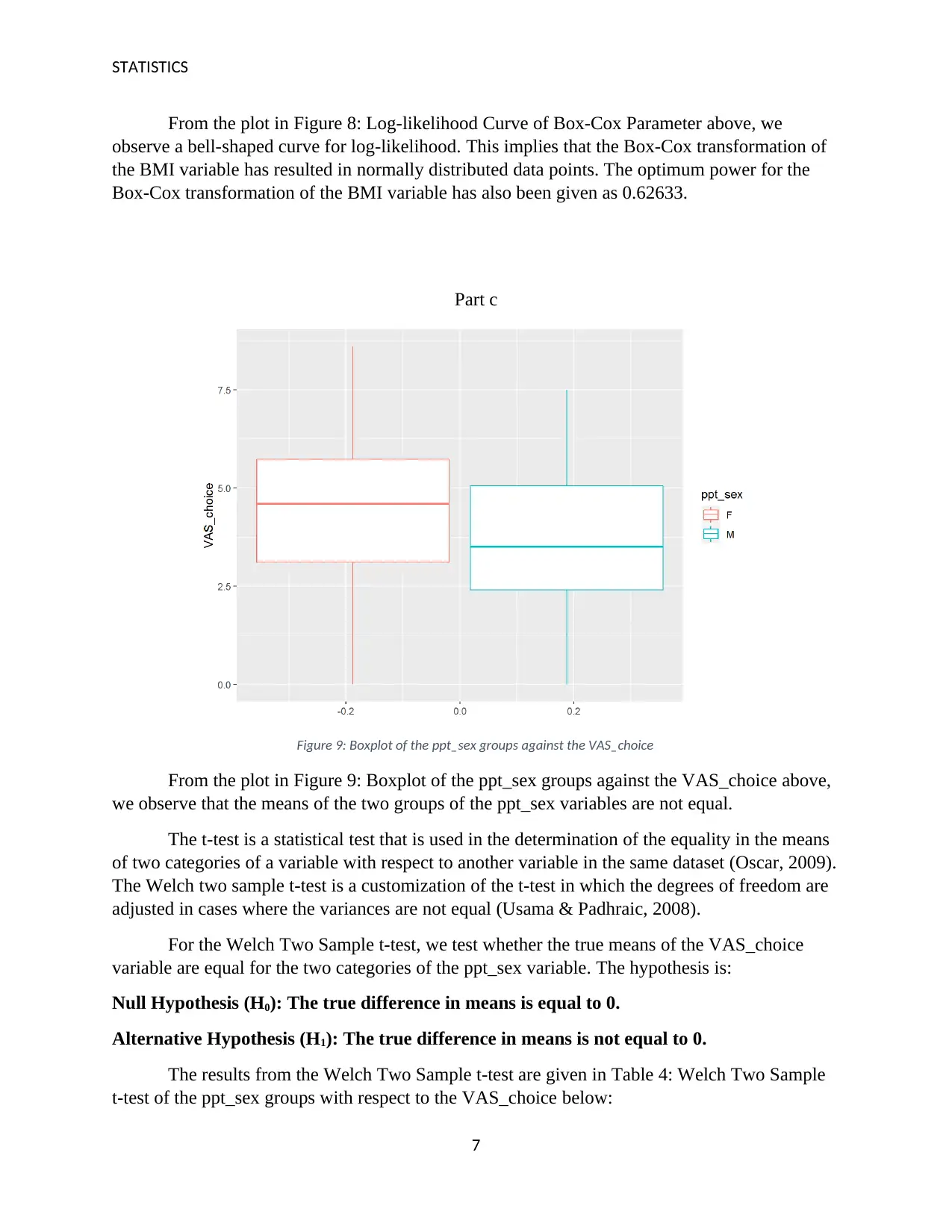
Figure 9: Boxplot of the ppt_sex groups against the VAS_choice
From the plot in Figure 9: Boxplot of the ppt_sex groups against the VAS_choice above,
we observe that the means of the two groups of the ppt_sex variables are not equal.
The t-test is a statistical test that is used in the determination of the equality in the means
of two categories of a variable with respect to another variable in the same dataset (Oscar, 2009).
The Welch two sample t-test is a customization of the t-test in which the degrees of freedom are
adjusted in cases where the variances are not equal (Usama & Padhraic, 2008).
For the Welch Two Sample t-test, we test whether the true means of the VAS_choice
variable are equal for the two categories of the ppt_sex variable. The hypothesis is:
Null Hypothesis (H0): The true difference in means is equal to 0.
Alternative Hypothesis (H1): The true difference in means is not equal to 0.
The results from the Welch Two Sample t-test are given in Table 4: Welch Two Sample
t-test of the ppt_sex groups with respect to the VAS_choice below:
7

STATISTICS
Table 4: Welch Two Sample t-test of the ppt_sex groups with respect to the VAS_choice
From Table 4: Welch Two Sample t-test of the ppt_sex groups with respect to the
VAS_choice above, we observe that at 95% confidence interval, the p-value is given as 2.666e-
10. This value is less than 0.05 (level of significance), hence we reject the null hypothesis and
conclude that the true difference in means is not equal to 0.
In the two sample t-test we assume that the dependent variable is normally distributed
(Galit, Peter, Inbal, Patel, & Kenneth, 2018). We also assume in the two sample t-test that the
variances are equal (Jaulin, 2010). This presents limitations in applying the two sample t-test for
this case. The VAS_choice variable is not normally distributed as seen from the Shapiro-Wilk
test in Table 1: Shapiro-Wilk Test for VAS_choice. We are also not certain as to whether the
variance in the two categories of the ppt_sex variable with respect to the VAS_choice variable is
equal. Application of the Welch Two Sample t-test however caters for the uncertainty in the
equality of the variance.
Part d
Figure 10: Boxplot of Joint Effect of ppt_sex and Site on VAS_choice
8

STATISTICS
From the plot in Figure 10: Boxplot of Joint Effect of ppt_sex and Site on VAS_choice
above we observe the boxplots for the four interactions between the categories of the ppt_sex
and Site variables. Under the F (Female) category of the ppt_sex variable, the two Site variable
categories (multiple and single) appear to have means that are not equal. Under the M (Male)
category of the ppt_sex variable, the two Site variable categories (multiple and single) appear to
have means that are almost equal.
Figure 11: Scatter Plots for the Joint Effect of ppt_sex and Site on VAS_choice
From the plot in Figure 11: Scatter Plots for the Joint Effect of ppt_sex and Site on
VAS_choice above we observe that the four interactions between the categories of the ppt_sex
and Site variables show not particular trend. The data points do not follow an identifiable trend,
however, many data points fall between the range of 0 to 7.5 with a few falling outside the range.
9

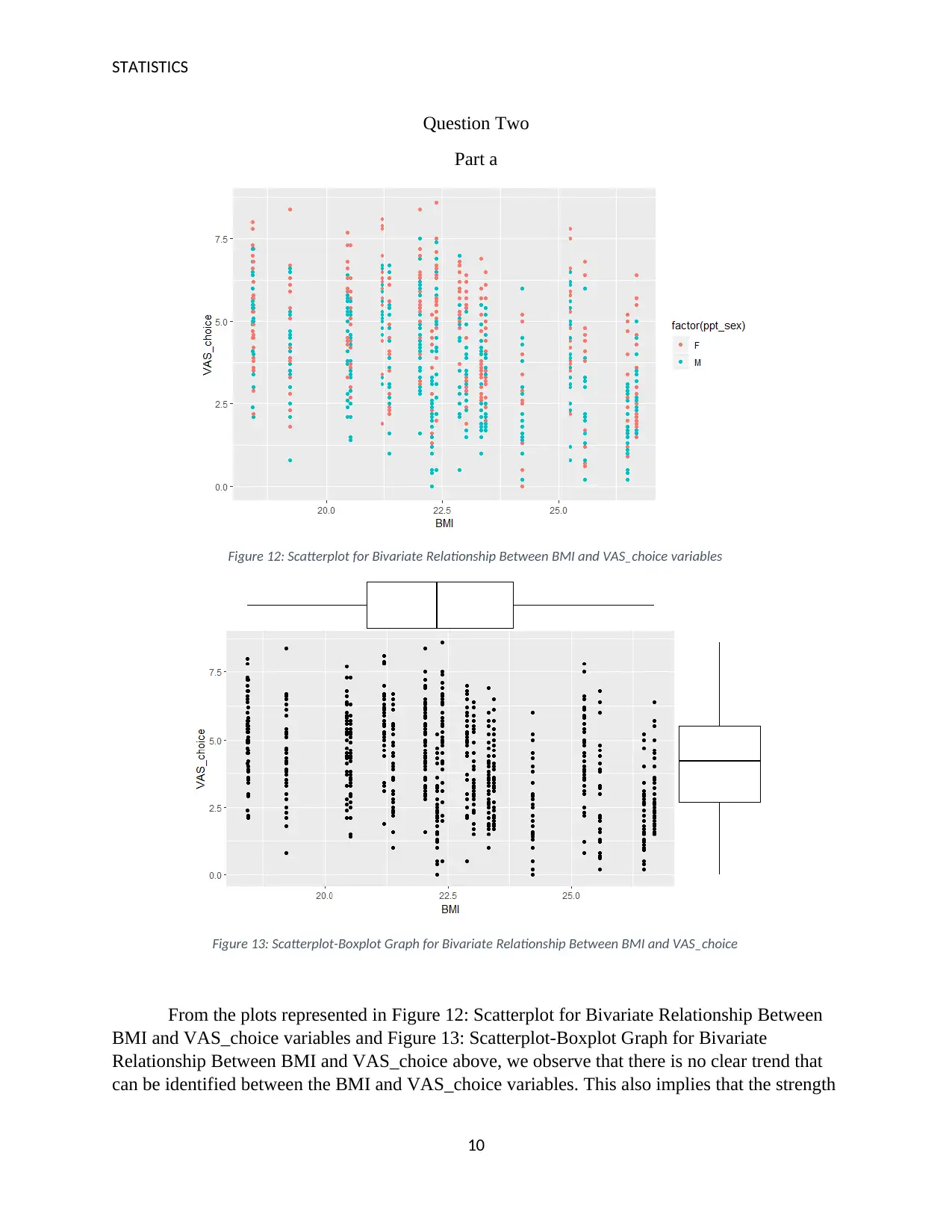
STATISTICS
Question Two
Part a
Figure 12: Scatterplot for Bivariate Relationship Between BMI and VAS_choice variables
Figure 13: Scatterplot-Boxplot Graph for Bivariate Relationship Between BMI and VAS_choice
From the plots represented in Figure 12: Scatterplot for Bivariate Relationship Between
BMI and VAS_choice variables and Figure 13: Scatterplot-Boxplot Graph for Bivariate
Relationship Between BMI and VAS_choice above, we observe that there is no clear trend that
can be identified between the BMI and VAS_choice variables. This also implies that the strength
10

STATISTICS
of any relationship that may exist between the BMI and VAS_choice variables is significantly
weak.
We also observe from the Figure 12: Scatterplot for Bivariate Relationship Between BMI
and VAS_choice variables that for the same value of the BMI, the values of the VAS_choice for
the male category is more likely be lower than that for the female category. This is evident from
the concentration of data points for the male category at the bottom of the graph while the
concentration of data points for the female category at the top of the graph. However, we can say
that for both categories of the ppt_sex variable, there is no indication of existence of a definable
relationship between the BMI and VAS_choice variables.
Outliers are data points or observations in a dataset that show significant difference in
measurement or magnitude in comparison to majority of other observations in the same dataset
(Schubert, Zimek, & Kriegel, 2012). Outliers can be observed on both plots and are present at the
0-point mark of the VAS_choice variable as well at and above the 7.5-point mark of the
VAS_choice variable. The presence of these outlier values may affect the results of statistical
analysis (Zimek, Schubert, & Kriegel, 2012). They may also result in test assumptions not being
met.
Part b
The summary of the model for fitted resistant line of VAS_choice vs BMI for the F
(Female) category of the ppt_sex is given in Table 5: Fitted Resistant Line Summary for the F
category of the ppt_sex variable below:
Table 5: Fitted Resistant Line Summary for the F category of the ppt_sex variable
From Table 5: Fitted Resistant Line Summary for the F category of the ppt_sex variable
we observe that the value of the y intercept = 13.447 while the value of the slope =-0.395.
11

STATISTICS
Figure 14: Plot of Resistant Line for F category of the ppt_sex variable
From Figure 14: Plot of Resistant Line for F category of the ppt_sex variable above, we
observe that not all the data points fall on the resistant line, this thus implies that the model is not
appropriated for the data. The model has the limitation of not capturing all the data points in the
data.
The summary of the model for fitted resistant line of VAS_choice vs BMI for the M
(Male) category of the ppt_sex is given in Table 6: Fitted Resistant Line Summary for the M
category of the ppt_sex variable below:
Table 6: Fitted Resistant Line Summary for the M category of the ppt_sex variable
From Table 6: Fitted Resistant Line Summary for the M category of the ppt_sex variable
above we observe that the value of the y intercept = 13.723 while the value of the slope =-0.447.
12

STATISTICS
Figure 15: Plot of Resistant Line for M category of ppt_sex variable
From Figure 15: Plot of Resistant Line for M category of ppt_sex variable above, we
observe that not all the data points fall on the resistant line, this thus implies that the model is not
appropriated for the data. The model has the limitation of not capturing all the data points in the
data.
13

STATISTICS
Part c
The summary of the model for fitted resistant line of VAS_choice on BMI for the F
(Female) category of the ppt_sex is given in Table 7: Regression Summary for F category of
ppt_sex variable below:
Table 7: Regression Summary for F category of ppt_sex variable
From Table 7: Regression Summary for F category of ppt_sex variable we observe that
the y intercept =10.89102 while the slope = -0.28563. At 0.05 level of significance, the BMI
variable is significant in the model. The value of the Adjusted R-squared = 0.1443, this implies
that the model explains only 14.43% of the relationship between the variables in the model. This
percentage is small and hence the model cannot be described as appropriate for the data. This
limits the application of the model for inference of the relationship between the two variables.
The summary of the model for fitted resistant line of VAS_choice on BMI for the M
(Male) category of the ppt_sex is given in Table 8: Regression Summary for M category of the
ppt_sex variable below:
Table 8: Regression Summary for M category of the ppt_sex variable
14

STATISTICS
From Table 8: Regression Summary for M category of the ppt_sex variable we observe
that the y intercept =10.36816 while the slope = -0.29702. At 0.05 level of significance, the BMI
variable is significant in the model. The value of the Adjusted R-squared = 0.1722, this implies
that the model explains only 17.22% of the relationship between the variables in the model. This
percentage is small and hence the model cannot be described as appropriate for the data. This
limits the application of the model for inference of the relationship between the two variables.
Part d
Figure 16: Comparison Plot for Resistant Lines and Regression Lines
From the plot in Figure 16: Comparison Plot for Resistant Lines and Regression Lines,
the lines in black represent the resistant lines while those in blue represent the regression lines.
We observe that the two sets of lines differ both in slope and y intercept. The lines for the
respective categories of the ppt_sex variables do share the same data point for when the value of
the BMI = 22.5.
15

STATISTICS
Part e
Here we apply the multiple linear regression analysis. The multiple linear regression
analysis is statistical analysis technique that represents the relationship between more than two
variables in an equation form (Smith, Martinez, & Giraud-Carrier, 2014).
The summary for the model for evaluating the relationship between the dependent
variables; VAS_choice and the independent variables; BMI and WHR is given in Table 9:
Summary of Regression Model of BMI and WHR on VAS_choice below;
Table 9: Summary of Regression Model of BMI and WHR on VAS_choice
From Table 9: Summary of Regression Model of BMI and WHR on VAS_choice above,
we observe that the intercept =18.21934 while the coefficient for BMI = -0.23458 and the
coefficient for WHR = -11.88907. At 0.05 level of significance, the BMI and WHR variables are
both significant in the model. The value of the Adjusted R-squared = 0.2251, this implies that the
model explains only 14.43% of the relationship between the variables in the model. This
percentage is small and hence the model cannot be described as appropriate for the data.
Therefore, the BMI and WHR can be said to be poor predictors of attractiveness.
16

STATISTICS
References
Barbara, I., & Susan, D. (2014). Introductory Statistics (1st ed.). New York: OpenStax CNX.
Galit, S., Peter, B. C., Inbal, Y., Patel, N. R., & Kenneth, L. C. (2018). Data Mining for Business
Analytics (1st ed.). New Delhi: John Wiley & Sons, Inc.
Han, K., & Jaiwei, P. (2011). Data Mining: Concepts and Techniques (3rd ed.). London: Morgan
Kaufman.
Jaulin, L. (2010). Probabilistic set-membership approach for robust regression. 5(1). Journal of
Statistical Theory and Practice, 1-14.
Kabacoff, R. I. (2017, March 15). graphs. Retrieved from statmethods:
www.statmethods.net/graphs/density.html
Kirk, A. (2016). Data Visualization: A Handbook for Data Driven Design (2nd ed.). Thousand
Oaks, CA: Sage Publications, Ltd.
Martinez, W. L., Martinez, A. R., & Solka, J. (2010). Exploratory Data Analysis With MATLAB,
2nd Edition (1 ed.). London: CRC/Chapmann & Hall.
Nornadiah, R., & Bee, W. Y. (2011). Power Comparisons of Shapiro-Wilk, Kolmogorov,
Lilliefors and Anderson-Darling Tests. Journal of Statistical Modelling and Analytics ,
21-33. 2(1).
O'Neil, C., & Schutt, R. (2013). Doing Data Science (3rd ed.). London: O'Reily.
Oscar, M. (2009). A data mining and knowledge discovery process model (1st ed.). Vienna: Julio
Ponce.
Reips, U. D., & Frederik, F. (2008). Interval Level Measurement with Visual Analogue Scales in
Internet-based Research: VAS Generator. Behaviour Research Methods, 40(3), 699-704.
Roles, R., Baeten, Y., & Signer, B. (2016). Interactive and Narrative Data Visualization for
Presentation-Based Knowledge Transfer. Communication in Computer and Information
Science, 4(6), 739.
Schubert, E., Zimek, A., & Kriegel, H. P. (2012). Local outlier detection reconsidered: A
generalized view on locality with applications to spatial, video, and network outlier
detection. 28. Data Mining and Knowledge Discovery, 190-237.
Smith, M. R., Martinez, T., & Giraud-Carrier, C. (2014). An Instance Level Analysis of Data
Complexity. 95(2). Machine Learning, 225-256.
Theus, M., & Urbanek, S. (2008). Inteactive Graphics For Data Analysis (1st ed.). Boca Raton:
CRC Press.
Ulf-Dietrich, R., & Uwe, M. (2014). Mining "Big Data" Using Big Data Services. International
Journal of Internet Science, 1(1), 1-8.
17

STATISTICS
Usama, F., & Padhraic, S. (2008). From data mining to Knowledge Discovery in Databases (4th
ed.). New York: CRC Press.
Vicenc, T. (2017). Studies in Big Data (1st ed.). Chicago: Springer International Publishing .
Witten, I. H. (2011). Data Mining: Practical Machine Learning Tools (3rd ed.). Sydney :
Morgan Kaufmann.
Zimek, A., Schubert, E., & Kriegel, H. P. (2012). A survey on unsupervised outlier detection in
high-dimensional numerical data. 5(5). Statistical Analysis and Data Mining, 363-387.
18