Thesis Proposal and Research Project

The provided document outlines the details of a thesis proposal and research project. It includes a Gantt chart with specific dates for tasks such as supervisor meetings, draft preparation, presentation, and interim report submission. The project has a budget of $0, supplied by the university, and utilizes materials like MATLAB software, internet resources, and library facilities. References to previous studies on radiative transfer equations, Lévy kinetics, and photon propagation are also provided.

UNIVERSITY AFFILIATION
FACULTY & DEPARTMENT
COURSE NAME
COURSE CODE
TITLE:
INVERSION OF THE RADIATIVE TRANSFER EQUATION USING MACHINE
LEARNING TECHNIQUES
STUDENT NAME
STUDENT REGISTRATION NUMBER
DATE OF SUBMISSION

ABSTRACT
In atmospheric sciences, the impact of smog and environmental pollutants are investigated by analyzing
solar radiation propagating through the atmosphere. Radiative heat transfer plays an important role in the optimal
design of furnaces and radiators. In medical diagnostics using optical methods, the propagation of electromagnetic
radiation is used to characterize tissue and blood for example, to screen for cancer and to monitor wounds. More
recently, this approach is also being considered for characterizing chemical suspensions and powder mixtures. In all
these applications, radiative transfer theory (RTT) is used to describe the propagation of radiation energy. The
radiative transfer equation (RTE) arising out of this theory is computationally intensive particularly if the intention
is to extract the radiative transfer coefficients which contain information regarding the characteristics of the medium
through which the radiation has travelled. In this study, the RTE solution will be obtained by using machine learning
techniques such as Neural Networks and Support Vector Machines. The performance of these methods will be
compared for solving the RTE under different conditions. This work will be carried out using MATLAB and the
machine learning toolbox available in MATLAB.
TABLE OF CONTENTS
1

ABSTRACT................................................................................................................................................1
INTRODUCTION.......................................................................................................................................3
PROBLEM DEFINITION AND SCOPE....................................................................................................6
APPROACH AND METHODS..................................................................................................................6
MATERIALS..............................................................................................................................................6
PROJECT PLAN AND MILESTONES......................................................................................................8
GANTT CHART.......................................................................................................................................10
PROJECT BUDGET.................................................................................................................................11
PROJECT DELIVERABLES....................................................................................................................11
PROJECT RESOURCES..........................................................................................................................11
INTRODUCTION
Neural networks
2

The neural network approach is adopted from the biological to artificial neurons and it consists
of dendrites, soma, axon, synapse, and the neuron activates after a certain threshold is met. The
learning occurs through the electronic and chemical changes in the effectiveness of synaptic
junction. An artificial neuron is simulated on hardware or by software. The input connections
and the receives as well as the node, unit, or PE simulates neuron body, output connection as the
transmit. The activation function employs a threshold or bias and the connection weights act as
synaptic junctions. Basic function of neuron is to sum inputs and produce output given sum is
greater than threshold. ANN node produces an output as follows:
(i) Multiplies each component of the input pattern by the weight of its connection.
(ii) Sums all weighted inputs and subtracts the threshold value implies total weighted
input.
(iii) Transforms the total weighted input into the output using the activation function.
The limitations of perceptron is the ability to form only linear discriminate functions such as the
classes which can be divided by a line or hyper-plane. The most functions are more complex as
they tend to be non-linear or not linearly separable. The combined results of two neurons can
produce good classification. More complex multi-layer networks are needed to solve more
difficult problems. In the multi-layer feed forward, Artificial Neural Networks have hidden layer
of nodes allowed combinations of the linear functions. The non-linear activation functions
displayed properties closer to real neurons where the output varies continuously but not linearly.
The non-linear ANN classifier is possible. There was no learning algorithm to adjust the weights
of a multilayer network and the weights have to be set. One of the most common ANN learning
algorithm is the back propagation whose error is sent back through the network to correct all
weights. Similarly, to the perceptron, the calculation of error here is based on the difference
3

between the target and the yield. The back propagation is therefore, the rate of change of the
error which is the most vital feedback through the network. The generalized delta rule relies on
the sigmoid activation function for communication. The cell body performs a weighting
algebraic sum or integration of the input signals. If the result exceeds a certain threshold value
then the neuron becomes active and produces a potential action which is sent to the axon. If it
does not exceed the threshold value, the neuron remains in idle state. An artificial neural network
receives external signals on one input layer of nodes, each of which is connected with a number
of internal nodes, organized in several levels. Each node processes the received signals and
transmits the result to succeeding nodes. An artificial neuron is the fundamental calculus unit of
the neural network and in the neural model it is formed from three basic elements.
Neural network spectroscopy
Applications of multi-layer feed-forward artificial neural networks (ANN) to spectroscopy are
reviewed. Network architecture and training algorithms are discussed. Back-propagation, the
most commonly used training algorithm, is analyzed in greater detail. The following types of
applications are considered: data reduction by means of neural networks, pattern recognition,
multivariate regression, robust regression, and handling of instrumental drifts (Cirovic).
Neural network optical properties
In the linear optic, there is a transient phenomenon that has no effect on anything. In the
transparent volume of a non-linear optical medium. The interference pattern causes a change in
the refractive index of the non-linear medium in the shape of those same parallel planes. An
optical perceptron with a soft optical threshold is implemented and trained with an adapted Back
propagation algorithm. The optical thresholding perceptron is composed of two section named
4

matrix-vector-multiplier and a thresholding device (Steck1, Skinner, Cruz-Cabrera, Yang, &
Behrman).
Working principle of neural networks
In the early learning phase, the artificial neural network is presented with input data set and
trained to fire out the desired values at the output layer. The training algorithm iteratively
modifies weights on connections through which signals are transmitted in order to minimize the
gap between network output and desired one. The autoencoder model is an auto associative
neural network encoder or simply autoencoder has the auto associative feature and bottleneck
layer. The learning algorithm for Neural Networks requires certain parameters such as the
learning rate, momentum, type of activation function of each neuron, error calculation function
and the network topology to train and test. In this work, the first goal to achieve is to find a
structure of adequate network while the optimization of the parameters remains a secondary
aspect. In fact, considering the type of data and physical principles that characterize them, it is
seen that spectra values are ranging in the intervals centered at 0 where there is the absence of
scattering (Munshi, Cummingham, Linfield , Davies, & Edwards, 2009).
MATLAB simulation of neural networks
The scalar input is multiplied with the scalar weight to form one of the terms that is sent to the
summer. The other input is multiplied by a bias and then it is passed to the summer. The summer
output, which is also referred to as the net input, goes into a transfer function which produces the
scalar neuron output.
5

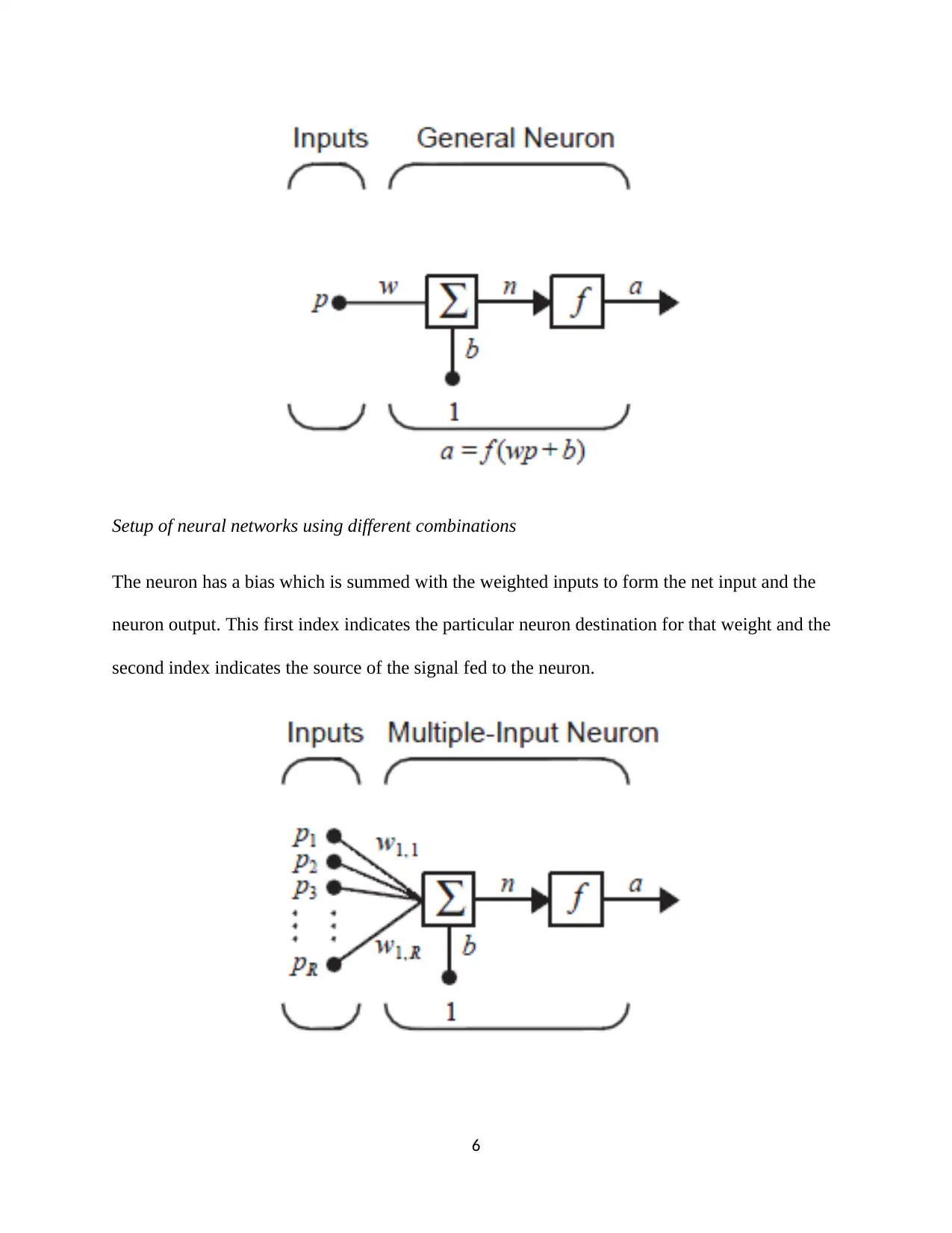
Setup of neural networks using different combinations
The neuron has a bias which is summed with the weighted inputs to form the net input and the
neuron output. This first index indicates the particular neuron destination for that weight and the
second index indicates the source of the signal fed to the neuron.
6

The layer includes the weight matrix, W, the summers, the bias vector, b, the transfer function
boxes and the output vector a. each layer has its own weight matrix, its own bias vector, a net
input vector and an output vector. The number of the layer as a superscript to the names for each
of these variables. A layer whose output is the network output is the output layer and all the other
layers tend to be hidden.
PROBLEM DEFINITION AND SCOPE
The main problem, in the quantitative analysis of turbid samples using near-infrared (NIR)
spectroscopy, is that multivariate calibration models built on conventional spectroscopic
measurements such as transmittance or reflectance are adversely affected by variations arising
from multiple light scattering, because these variations are not necessarily related to changes
in chemical information, i.e., concentrations of chemical components.
7

APPROACH AND METHODS
The approach adopted for the transfer equation for the radiative theory is one to investigate the
spectroscopy of the materials. Another approach that was adopted was the RTE-Based Scatter
Correction and Calibration Approach. It was the proposed methodology for estimation of
concentrations of chemical components in suspensions. The method involves
(i) Acquisition of the bulk optical properties
(ii) Extraction of pertinent chemical information
The AD method is much faster but does not take into account beam width and assumes that the
sample is of infinite width, thus ignoring any light loss through the sides of the sample which in
some cases could lead to significant errors (Dzhongava, Thennadil, & S, 2009).
MATERIALS
 Simulated data from using radiative transfer theory
 MATLAB R2017b software
8

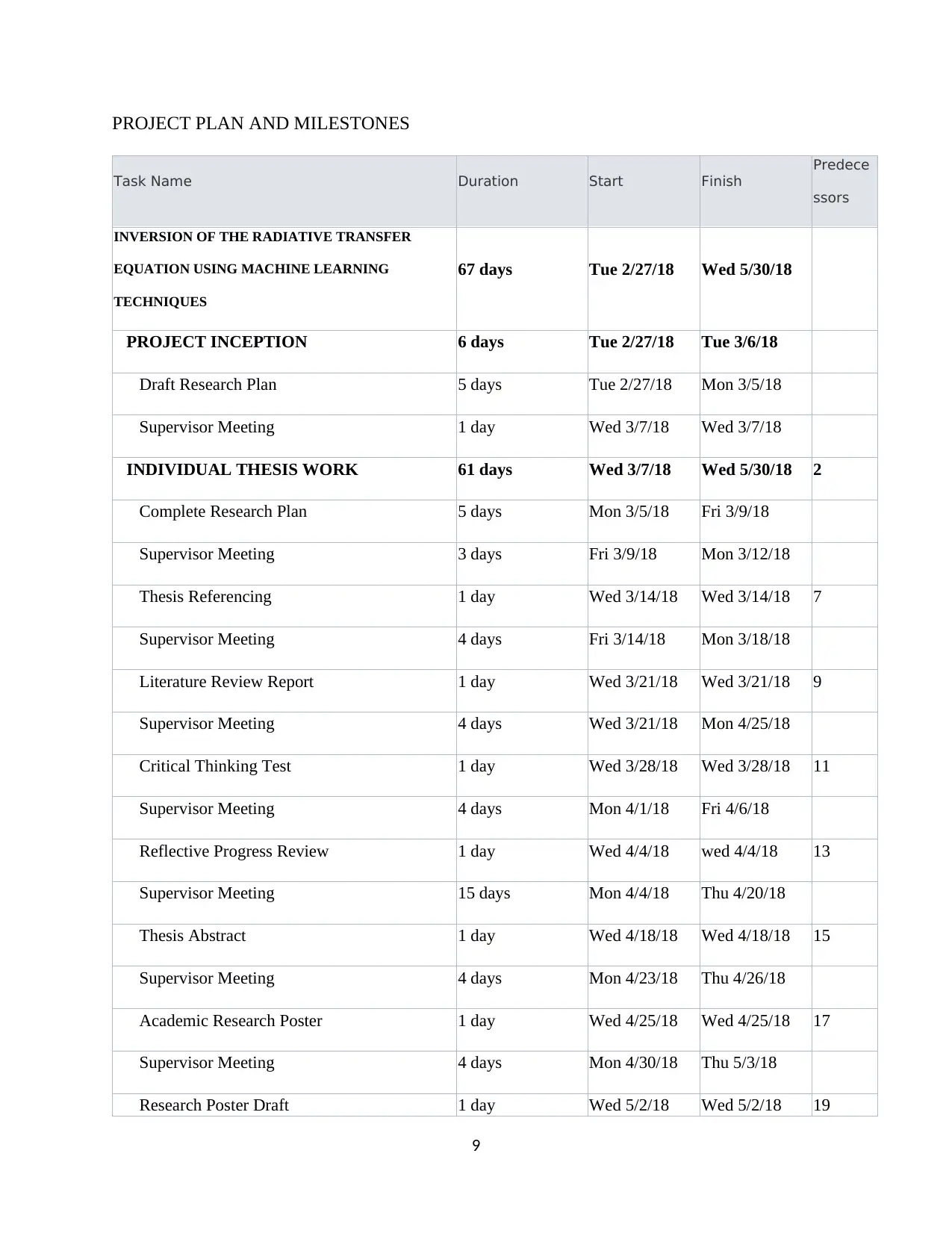
PROJECT PLAN AND MILESTONES
Task Name Duration Start Finish
Predece
ssors
INVERSION OF THE RADIATIVE TRANSFER
EQUATION USING MACHINE LEARNING
TECHNIQUES
67 days Tue 2/27/18 Wed 5/30/18
PROJECT INCEPTION 6 days Tue 2/27/18 Tue 3/6/18
Draft Research Plan 5 days Tue 2/27/18 Mon 3/5/18
Supervisor Meeting 1 day Wed 3/7/18 Wed 3/7/18
INDIVIDUAL THESIS WORK 61 days Wed 3/7/18 Wed 5/30/18 2
Complete Research Plan 5 days Mon 3/5/18 Fri 3/9/18
Supervisor Meeting 3 days Fri 3/9/18 Mon 3/12/18
Thesis Referencing 1 day Wed 3/14/18 Wed 3/14/18 7
Supervisor Meeting 4 days Fri 3/14/18 Mon 3/18/18
Literature Review Report 1 day Wed 3/21/18 Wed 3/21/18 9
Supervisor Meeting 4 days Wed 3/21/18 Mon 4/25/18
Critical Thinking Test 1 day Wed 3/28/18 Wed 3/28/18 11
Supervisor Meeting 4 days Mon 4/1/18 Fri 4/6/18
Reflective Progress Review 1 day Wed 4/4/18 wed 4/4/18 13
Supervisor Meeting 15 days Mon 4/4/18 Thu 4/20/18
Thesis Abstract 1 day Wed 4/18/18 Wed 4/18/18 15
Supervisor Meeting 4 days Mon 4/23/18 Thu 4/26/18
Academic Research Poster 1 day Wed 4/25/18 Wed 4/25/18 17
Supervisor Meeting 4 days Mon 4/30/18 Thu 5/3/18
Research Poster Draft 1 day Wed 5/2/18 Wed 5/2/18 19
9

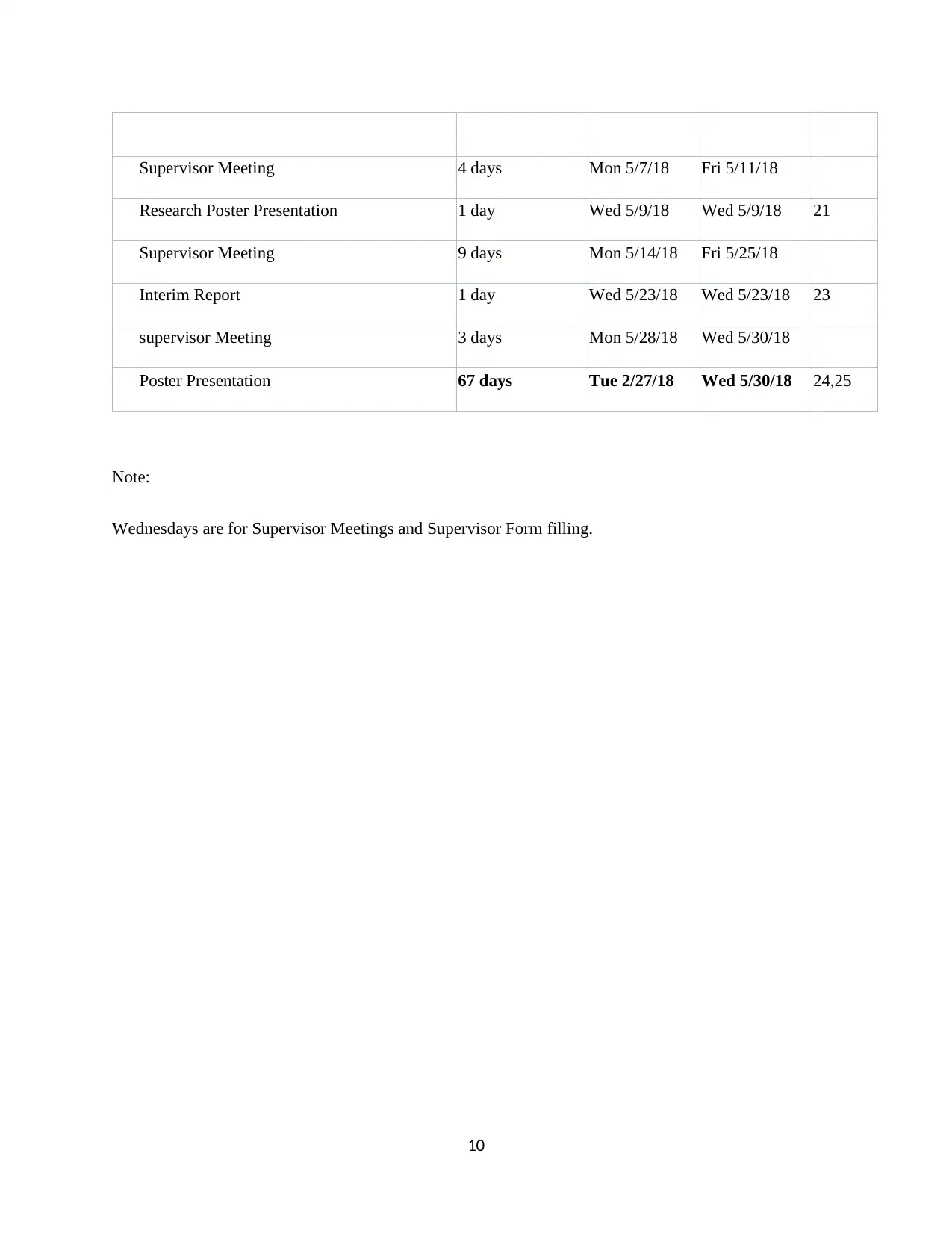
Supervisor Meeting 4 days Mon 5/7/18 Fri 5/11/18
Research Poster Presentation 1 day Wed 5/9/18 Wed 5/9/18 21
Supervisor Meeting 9 days Mon 5/14/18 Fri 5/25/18
Interim Report 1 day Wed 5/23/18 Wed 5/23/18 23
supervisor Meeting 3 days Mon 5/28/18 Wed 5/30/18
Poster Presentation 67 days Tue 2/27/18 Wed 5/30/18 24,25
Note:
Wednesdays are for Supervisor Meetings and Supervisor Form filling.
10

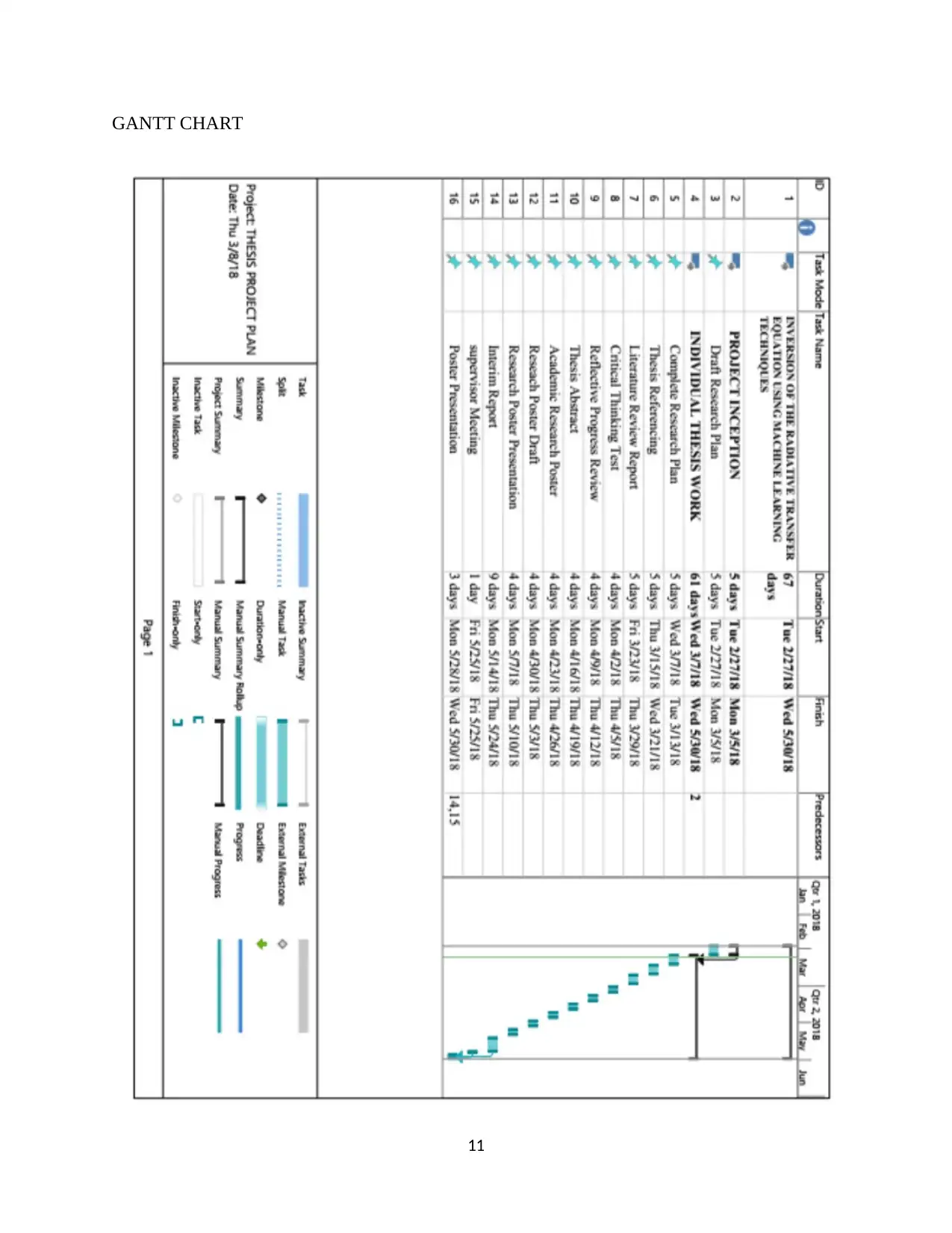
GANTT CHART
11

PROJECT BUDGET
The project budget as estimated for this project is $0 as supplied by the university for the entire
work. It is crucial to note, however, that the Thesis proposal report does not attract any project
costs.
PROJECT DELIVERABLES
The following items will be delivered at completion of the thesis project:
 Thesis Journal
 Supervisor meeting minutes
 Thesis Proposal Document
 Thesis Report
 Presentation Slides
PROJECT RESOURCES
The following materials will be utilized in the research process of the thesis design:
 The MATLAB R2017b Software
 Internet website and Peer-reviewed Journals
 The University Library
 The center for Neural Networks Machine Learning Website
12

REFERENCES
Dzhongava, E. H., Thennadil, C. R., & S. N. (2009). Applied Spectroscopy. 25-32.
Raimundas, S., & Thennadil, S. (2009). Radiative Transient Equations Theory. Analytical
Chemistry, 1-11.
Davis, A., and A. Marshak, Lévy kinetics in slab geometry: Scaling of transmission probability,
in Fractal Frontiers, M. M. Novak and T. G. Dewey (eds.), World Scientific, Singapore, pp. 63-
72 (1997).
Buldyrev, S. V., S. Havlin, A. Ya. Kazakov, M. G. E. da Luz, E. P. Raposo, H. E. Stanley, and
G. M. Viswanathan, Average time spent by Lévy flights and walks on an interval with absorbing
boundaries, Phys. Rev. E, 64, 41108-41118 (2001).
Davis, A. B., and A. Marshak, Photon propagation in heterogeneous optical media with spatial
correlations: Enhanced mean-free-paths and wider-than-exponential free-path distributions, J.
Quant. Spectrosc. Rad. Transf., 84, 3-34 (2004).
Davis, A. B., and H. W. Barker, Approximation methods in three-dimensional radiative transfer,
in Three-Dimensional Radiative Transfer for Cloudy Atmospheres, A. Marshak and A. B. Davis
(eds.), Springer-Verlag, Heidelberg (Germany), to appear (2004).
Buldyrev, S. V., S. Havlin, A. Ya. Kazakov, M. G. E. da Luz, E. P. Raposo, H. E. Stanley, and
G. M. Viswanathan, 2001: Average time spent by Lévy flights and walks on an interval with
absorbing boundaries, Phys. Rev. E, 64, 41108-41118.
13