Inverted Pendulum: Designing a Controller for ROTPEN Kit
VerifiedAdded on 2023/04/21
|31
|3267
|118
AI Summary
This document provides a step-by-step guide on designing a controller for the ROTPEN kit to stabilize an inverted pendulum. It includes an introduction to the system, the aim of the project, and detailed instructions on building the Simulink model. The document also covers linearization of the system, full-state feedback, and MATLAB commands for control system design. It concludes with a discussion on the behavior of the inverted pendulum model and impulse input to the system.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

University
*** Semester
Inverted Pendulum
Student Name:
Register Number:
Submission Date:
*** Semester
Inverted Pendulum
Student Name:
Register Number:
Submission Date:
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Table of Contents
Question-1.................................................................................................................................................................... 1
Question-2.................................................................................................................................................................... 1
Question-3.................................................................................................................................................................... 2
Question-4.................................................................................................................................................................... 3
Question-5.................................................................................................................................................................... 5
Question-6.................................................................................................................................................................... 6
Question-7.................................................................................................................................................................... 8
Question-8.................................................................................................................................................................. 10
Question-9.................................................................................................................................................................. 12
Output Graphs............................................................................................................................................................... 14
Step Input to the System............................................................................................................................................ 14
Response of pendulum position to an Impulse Disturbance.........................................................................................15
Pole – zero map of the System..................................................................................................................................... 15
Step Response with estimator...................................................................................................................................... 16
Real Pole plot.............................................................................................................................................................. 16
Complex pole plot....................................................................................................................................................... 17
Real zero plot.............................................................................................................................................................. 17
Complex zero plot....................................................................................................................................................... 18
Integrator plot............................................................................................................................................................ 18
Differentiator Plot....................................................................................................................................................... 19
Notch filter with zero and pole plot............................................................................................................................. 19
Open loop of Bode plot............................................................................................................................................... 20
Open Loop of Nyquist Diagram.................................................................................................................................. 20
Closed Loop response of Bode and Nyquist plot..........................................................................................................21
Discrete -time system response of Inverted Pendulum.................................................................................................21
Input – Output Plot of Pendulum position...................................................................................................................22
Simulation of Simulink Model of the Inverted Pendulum............................................................................................22
Step response comparison........................................................................................................................................... 23
Change in position of pendulum at a point..................................................................................................................23
Impulse disturbance rejection in a pendulum..............................................................................................................24
Summary....................................................................................................................................................................... 24
References...................................................................................................................................................................... 25
Question-1.................................................................................................................................................................... 1
Question-2.................................................................................................................................................................... 1
Question-3.................................................................................................................................................................... 2
Question-4.................................................................................................................................................................... 3
Question-5.................................................................................................................................................................... 5
Question-6.................................................................................................................................................................... 6
Question-7.................................................................................................................................................................... 8
Question-8.................................................................................................................................................................. 10
Question-9.................................................................................................................................................................. 12
Output Graphs............................................................................................................................................................... 14
Step Input to the System............................................................................................................................................ 14
Response of pendulum position to an Impulse Disturbance.........................................................................................15
Pole – zero map of the System..................................................................................................................................... 15
Step Response with estimator...................................................................................................................................... 16
Real Pole plot.............................................................................................................................................................. 16
Complex pole plot....................................................................................................................................................... 17
Real zero plot.............................................................................................................................................................. 17
Complex zero plot....................................................................................................................................................... 18
Integrator plot............................................................................................................................................................ 18
Differentiator Plot....................................................................................................................................................... 19
Notch filter with zero and pole plot............................................................................................................................. 19
Open loop of Bode plot............................................................................................................................................... 20
Open Loop of Nyquist Diagram.................................................................................................................................. 20
Closed Loop response of Bode and Nyquist plot..........................................................................................................21
Discrete -time system response of Inverted Pendulum.................................................................................................21
Input – Output Plot of Pendulum position...................................................................................................................22
Simulation of Simulink Model of the Inverted Pendulum............................................................................................22
Step response comparison........................................................................................................................................... 23
Change in position of pendulum at a point..................................................................................................................23
Impulse disturbance rejection in a pendulum..............................................................................................................24
Summary....................................................................................................................................................................... 24
References...................................................................................................................................................................... 25


Question-1
ANSWER:
Introduction
The Rotary Inverted Pendulum is an exemplary control issue that is investigated
frequently as an undertaking in control courses because of its effectively created elements that
area mix of its multifaceted nature of control design 1. It is a system which is built using the
pendulum that is attached to the rotary arm’s end, which the motor controls. In general, the motor
includes the servomotor coupled, by using the gear-chain. The principle objective includes
keeping the pendulum in the upright position of unsteady equilibrium. The next objective
includes keeping the motor at the specifically mentioned angular position, when the first task is
being performed. Whereas, the last task includes destabilizing the motor starting from the
hanging position of the equilibrium which is not stable, with the goal to achieve the stability
range (i.e., here the mode controller could easily start the stabilization.) 2.
Aim
The aimincludesdesigning the controller for the ROTPEN kit, with the help of an
effective linearised pendulum model.
Question-2
ANSWER:
The below mentioned steps help to build the inverted pendulum model in Simulink, they
are 3,
1 P S A, "THE STABILIZATION OF FORCED INVERTED PENDULUM VIA FUZZY CONTROLLER",
in International Journal of Research in Engineering and Technology, vol. 05, 2016, 152-155.
2 J Babu & E Vargheese, "Stabilization of Rotary Arm Inverted Pendulum using State Feedback
Techniques", in International Journal of Engineering Research and, vol. V4, 2015.
3 H Ali, "Robust Stabilizing Controller Design for Inverted Pendulum System", in Jurnal Teknologi, vol. 71,
2014.
1
ANSWER:
Introduction
The Rotary Inverted Pendulum is an exemplary control issue that is investigated
frequently as an undertaking in control courses because of its effectively created elements that
area mix of its multifaceted nature of control design 1. It is a system which is built using the
pendulum that is attached to the rotary arm’s end, which the motor controls. In general, the motor
includes the servomotor coupled, by using the gear-chain. The principle objective includes
keeping the pendulum in the upright position of unsteady equilibrium. The next objective
includes keeping the motor at the specifically mentioned angular position, when the first task is
being performed. Whereas, the last task includes destabilizing the motor starting from the
hanging position of the equilibrium which is not stable, with the goal to achieve the stability
range (i.e., here the mode controller could easily start the stabilization.) 2.
Aim
The aimincludesdesigning the controller for the ROTPEN kit, with the help of an
effective linearised pendulum model.
Question-2
ANSWER:
The below mentioned steps help to build the inverted pendulum model in Simulink, they
are 3,
1 P S A, "THE STABILIZATION OF FORCED INVERTED PENDULUM VIA FUZZY CONTROLLER",
in International Journal of Research in Engineering and Technology, vol. 05, 2016, 152-155.
2 J Babu & E Vargheese, "Stabilization of Rotary Arm Inverted Pendulum using State Feedback
Techniques", in International Journal of Engineering Research and, vol. V4, 2015.
3 H Ali, "Robust Stabilizing Controller Design for Inverted Pendulum System", in Jurnal Teknologi, vol. 71,
2014.
1
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1) In the MATLAB command window type Simulink and it opens the Simulink
environment. Next,in Simulink open a new model window by selecting New >
Simulink > Blank Model of the open Simulink Start Page window or by
pressing Ctrl-N.
2) From the Simulink/User-Defined Functions library, 4 Fcn Blocks are inserted. The
following equations for , , , and are built by employing the blocks.
3) Every single Fcn block must be changed so that itmatches with its linked function.
4) From the Simulink/Continuous library4 Integrator blocks must be inserted. Every
single Integrator block’s output will be the system’s state variable, , , , and .
5) Every single Integrator block must be double-clicked for adding the “State Name:” of
the linked state variable. Next, the “Initial condition:”must be changedfor
(pendulum angle) to "pi", for representing that the pendulum starts to point straight up.
6) From the Simulink/Signal Routing library, 4 Multiplexer (Mux) blocks must be
inserted, for every single Fcn block.
7) From the Simulink/Sinks and Simulink/Sources libraries, 2 Out1 blocks and one In1
block must be inserted, respectively. Next, the labels must be double-clicked, as it
helps to change the names of the blocks. For "Position" of the cart and the "Angle" of
the pendulum, two outputs are provided when one input is for "Force" that is applied
on the cart.
8) Mux blocks’ each output is connected to the corresponding input of the Fcn block.
9) In the function blocks the below equations are filled 4.
( J eq+ M p r2 ) ¨θ + M p Lp rsinα ( ˙α )2−M p Lp rcosα ¨α=τ output−β1 ˙θ
4
3 M p Lp
2 ¨α −M p Lp rcosα ¨θ−Mp g Lp sinα=− β2 ˙α
τ output= Kt [ V m−Km ˙θ (t) ]
Rm
4 L Wan, J Lei & H Wu, "Design of LQR Controller for the Inverted Pendulum", in Advanced Materials
Research, vol. 1037, 2014, 221-224.
2
environment. Next,in Simulink open a new model window by selecting New >
Simulink > Blank Model of the open Simulink Start Page window or by
pressing Ctrl-N.
2) From the Simulink/User-Defined Functions library, 4 Fcn Blocks are inserted. The
following equations for , , , and are built by employing the blocks.
3) Every single Fcn block must be changed so that itmatches with its linked function.
4) From the Simulink/Continuous library4 Integrator blocks must be inserted. Every
single Integrator block’s output will be the system’s state variable, , , , and .
5) Every single Integrator block must be double-clicked for adding the “State Name:” of
the linked state variable. Next, the “Initial condition:”must be changedfor
(pendulum angle) to "pi", for representing that the pendulum starts to point straight up.
6) From the Simulink/Signal Routing library, 4 Multiplexer (Mux) blocks must be
inserted, for every single Fcn block.
7) From the Simulink/Sinks and Simulink/Sources libraries, 2 Out1 blocks and one In1
block must be inserted, respectively. Next, the labels must be double-clicked, as it
helps to change the names of the blocks. For "Position" of the cart and the "Angle" of
the pendulum, two outputs are provided when one input is for "Force" that is applied
on the cart.
8) Mux blocks’ each output is connected to the corresponding input of the Fcn block.
9) In the function blocks the below equations are filled 4.
( J eq+ M p r2 ) ¨θ + M p Lp rsinα ( ˙α )2−M p Lp rcosα ¨α=τ output−β1 ˙θ
4
3 M p Lp
2 ¨α −M p Lp rcosα ¨θ−Mp g Lp sinα=− β2 ˙α
τ output= Kt [ V m−Km ˙θ (t) ]
Rm
4 L Wan, J Lei & H Wu, "Design of LQR Controller for the Inverted Pendulum", in Advanced Materials
Research, vol. 1037, 2014, 221-224.
2
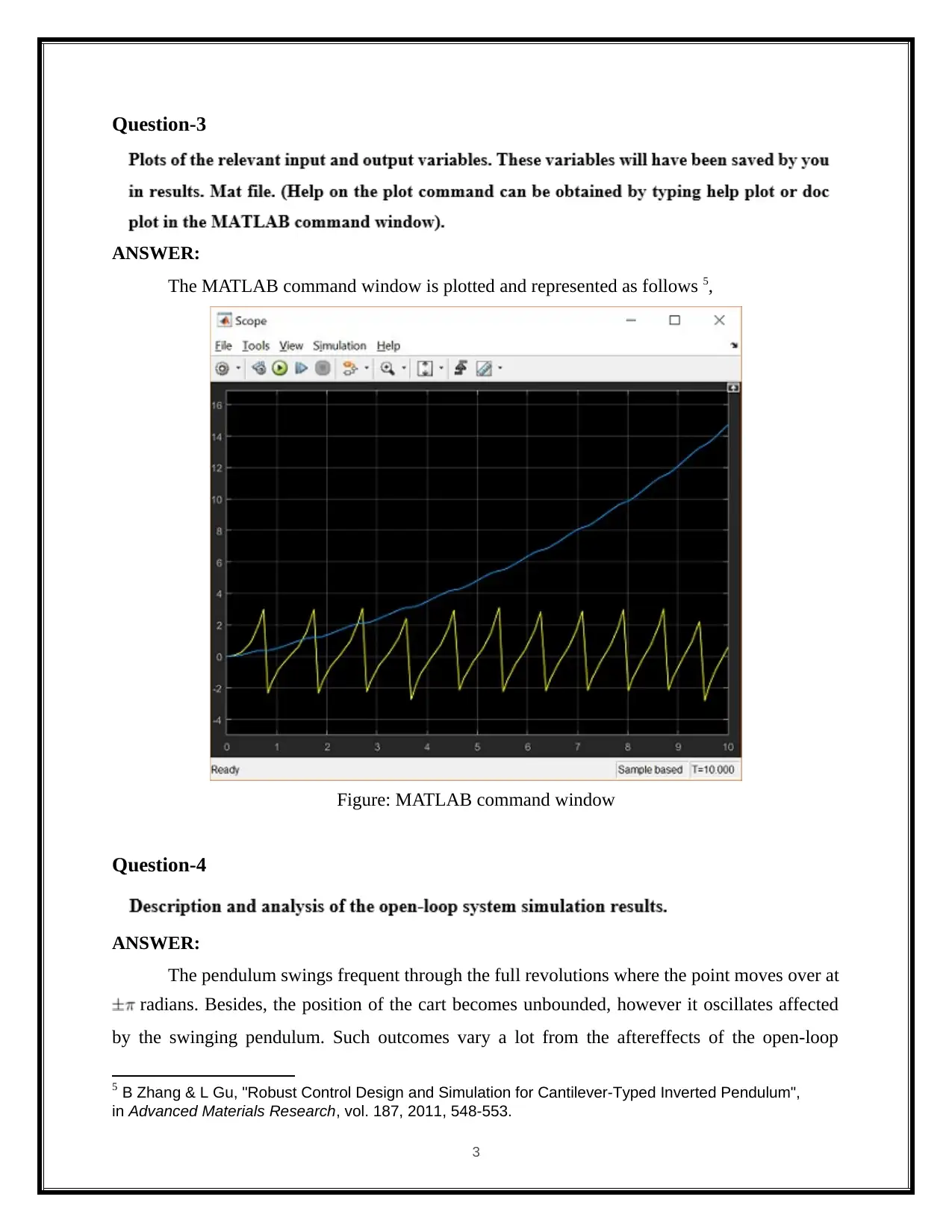
Question-3
ANSWER:
The MATLAB command window is plotted and represented as follows 5,
Figure: MATLAB command window
Question-4
ANSWER:
The pendulum swings frequent through the full revolutions where the point moves over at
radians. Besides, the position of the cart becomes unbounded, however it oscillates affected
by the swinging pendulum. Such outcomes vary a lot from the aftereffects of the open-loop
5 B Zhang & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted Pendulum",
in Advanced Materials Research, vol. 187, 2011, 548-553.
3
ANSWER:
The MATLAB command window is plotted and represented as follows 5,
Figure: MATLAB command window
Question-4
ANSWER:
The pendulum swings frequent through the full revolutions where the point moves over at
radians. Besides, the position of the cart becomes unbounded, however it oscillates affected
by the swinging pendulum. Such outcomes vary a lot from the aftereffects of the open-loop
5 B Zhang & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted Pendulum",
in Advanced Materials Research, vol. 187, 2011, 548-553.
3

simulation as mentioned at the beginning. This is expected obviously to the way that this
simulation utilized a completely nonlinear model 6.
Based on the pendulum’s reaction to the impulse of 1-Nsec implemented to the cart, the
pendulum’s design prerequisites are as follows:
1) For and the settling time is lower than 5 seconds
2) Pendulum angle will never be greater than 200 (0.35 radians) vertically.
In addition, the system’s response requirement for the 0.2-meter step command in the cart
position includes:
a) For and the settling time is lower than 5 seconds.
b) For the rise time is less than 0.5 seconds.
c) Pendulum angle will never be greater than 200 (0.35 radians) vertically.
Impulse response of the Open-loop
In the below equations, ‘v’ helps to return the poles and zeros as the column vectors.
The system’s zeros and poles where the pendulum position denotes the output are observed as
6 I Boussaada, I Morărescu & S Niculescu, "Inverted Pendulum Stabilization Via a Pyragas-Type
Controller: Revisiting the Triple Zero Singularity", in IFAC Proceedings Volumes, vol. 47, 2014, 6806-
6811.
4
simulation utilized a completely nonlinear model 6.
Based on the pendulum’s reaction to the impulse of 1-Nsec implemented to the cart, the
pendulum’s design prerequisites are as follows:
1) For and the settling time is lower than 5 seconds
2) Pendulum angle will never be greater than 200 (0.35 radians) vertically.
In addition, the system’s response requirement for the 0.2-meter step command in the cart
position includes:
a) For and the settling time is lower than 5 seconds.
b) For the rise time is less than 0.5 seconds.
c) Pendulum angle will never be greater than 200 (0.35 radians) vertically.
Impulse response of the Open-loop
In the below equations, ‘v’ helps to return the poles and zeros as the column vectors.
The system’s zeros and poles where the pendulum position denotes the output are observed as
6 I Boussaada, I Morărescu & S Niculescu, "Inverted Pendulum Stabilization Via a Pyragas-Type
Controller: Revisiting the Triple Zero Singularity", in IFAC Proceedings Volumes, vol. 47, 2014, 6806-
6811.
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

the following,
Time response can be retrieved from the poles of the system. Here, the system uses two transfer
functions, where the system contains a couple of outputs and a single input. Basically, all the
transfer functions work based on the input and output of the multi-input, multi-output (MIMO)
system which contains same poles, until there occurs a pole-zero cancellation.
Question-5
ANSWER:
The process of linearization comprises of producing the nonlinear system’s linear
approximation which is valid in a small region around the operating or trim point, a steady-state
5
Time response can be retrieved from the poles of the system. Here, the system uses two transfer
functions, where the system contains a couple of outputs and a single input. Basically, all the
transfer functions work based on the input and output of the multi-input, multi-output (MIMO)
system which contains same poles, until there occurs a pole-zero cancellation.
Question-5
ANSWER:
The process of linearization comprises of producing the nonlinear system’s linear
approximation which is valid in a small region around the operating or trim point, a steady-state
5
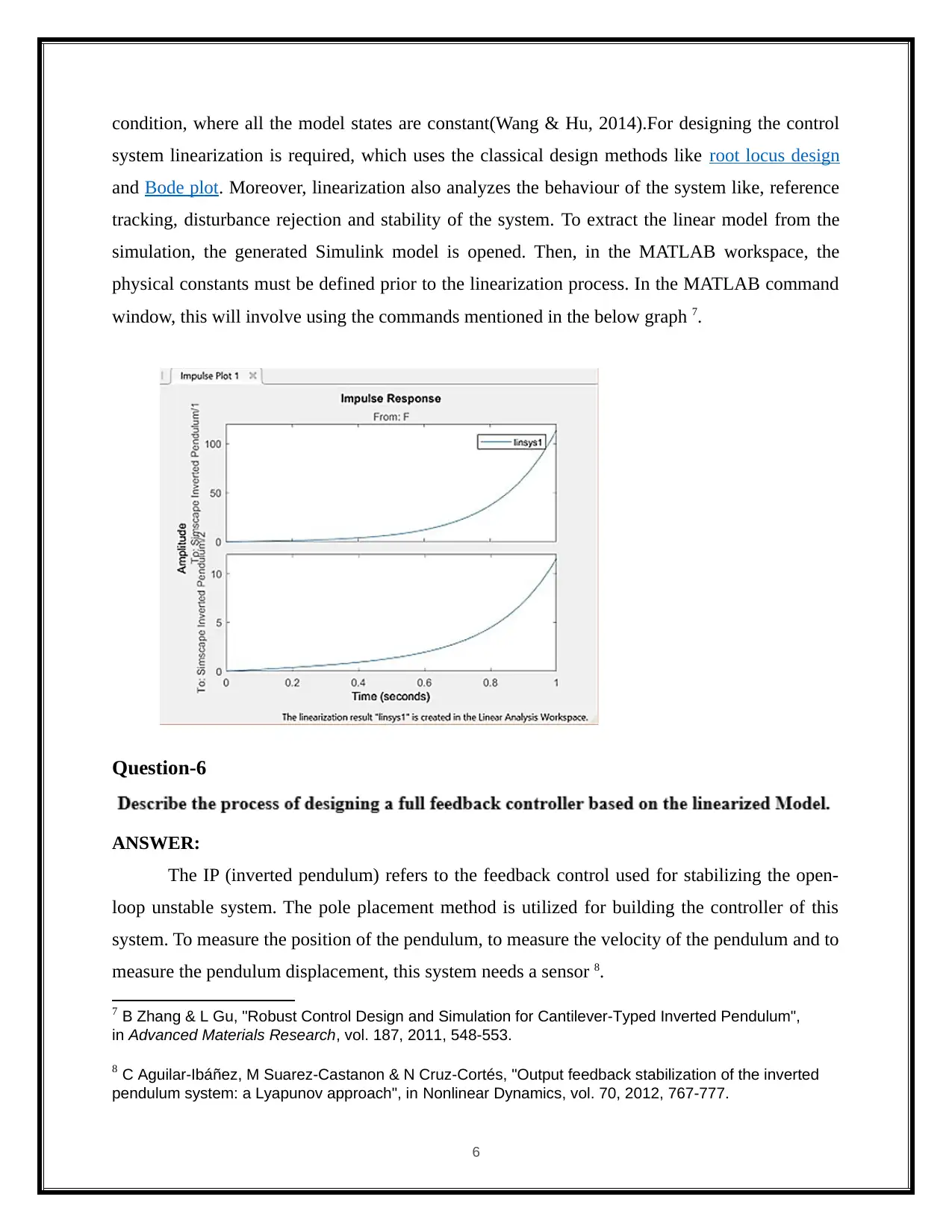
condition, where all the model states are constant(Wang & Hu, 2014).For designing the control
system linearization is required, which uses the classical design methods like root locus design
and Bode plot. Moreover, linearization also analyzes the behaviour of the system like, reference
tracking, disturbance rejection and stability of the system. To extract the linear model from the
simulation, the generated Simulink model is opened. Then, in the MATLAB workspace, the
physical constants must be defined prior to the linearization process. In the MATLAB command
window, this will involve using the commands mentioned in the below graph 7.
Question-6
ANSWER:
The IP (inverted pendulum) refers to the feedback control used for stabilizing the open-
loop unstable system. The pole placement method is utilized for building the controller of this
system. To measure the position of the pendulum, to measure the velocity of the pendulum and to
measure the pendulum displacement, this system needs a sensor 8.
7 B Zhang & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted Pendulum",
in Advanced Materials Research, vol. 187, 2011, 548-553.
8 C Aguilar-Ibáñez, M Suarez-Castanon & N Cruz-Cortés, "Output feedback stabilization of the inverted
pendulum system: a Lyapunov approach", in Nonlinear Dynamics, vol. 70, 2012, 767-777.
6
system linearization is required, which uses the classical design methods like root locus design
and Bode plot. Moreover, linearization also analyzes the behaviour of the system like, reference
tracking, disturbance rejection and stability of the system. To extract the linear model from the
simulation, the generated Simulink model is opened. Then, in the MATLAB workspace, the
physical constants must be defined prior to the linearization process. In the MATLAB command
window, this will involve using the commands mentioned in the below graph 7.
Question-6
ANSWER:
The IP (inverted pendulum) refers to the feedback control used for stabilizing the open-
loop unstable system. The pole placement method is utilized for building the controller of this
system. To measure the position of the pendulum, to measure the velocity of the pendulum and to
measure the pendulum displacement, this system needs a sensor 8.
7 B Zhang & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted Pendulum",
in Advanced Materials Research, vol. 187, 2011, 548-553.
8 C Aguilar-Ibáñez, M Suarez-Castanon & N Cruz-Cortés, "Output feedback stabilization of the inverted
pendulum system: a Lyapunov approach", in Nonlinear Dynamics, vol. 70, 2012, 767-777.
6

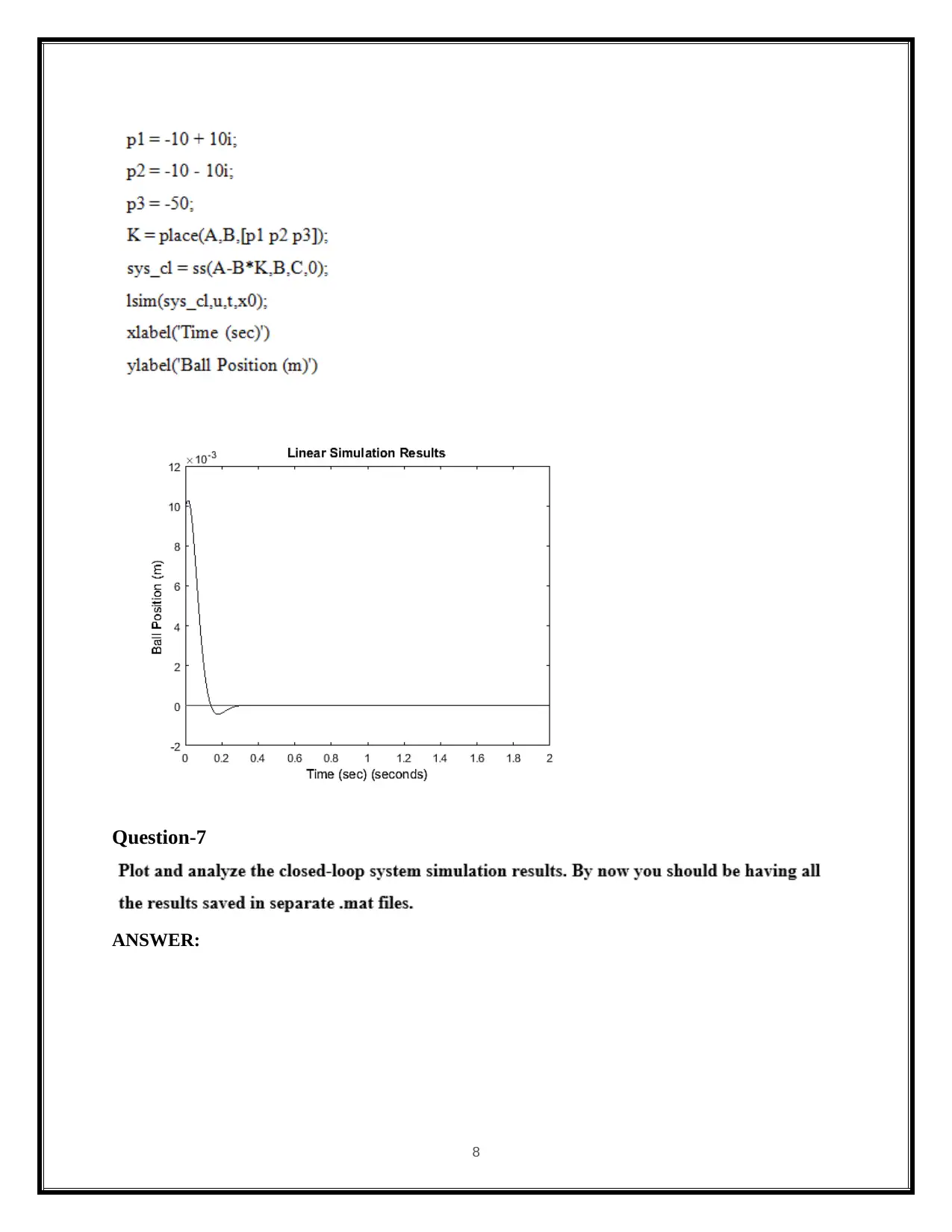
The full-state feedback system’s schematic is as follows 9.
Figure: Full-state feedback system
Here, the assumption includes that the reference is equivalent to zero, i.e., = 0. Thus, the input
is, (10)
Hence, for the closed-loop feedback system the equations of state-space are,
(11)
(12)
The closed-loop feedback system’s stability as well as the time-domain performance are
evaluated especially with the help of the eigenvalues’ location in the matrix ( )that are
equivalent to the closed-loop poles. There could be three poles in the system, as both the
matrices (i.e., and ) have 3x3 matrix. By choosing an appropriate state-feedback gain
matrix , we can place these The closed-loop poles could be placed anywhere if the state-
feedback gain matrix , is selected appropriately.
The state-feedback gain, , can be found by using the MATLAB function,, because it provides
the required closed-loop poles.
9 R Bitirgen, M Hancer & I Bayezit, "All Stabilizing State Feedback Controller for Inverted Pendulum
Mechanism", in IFAC-PapersOnLine, vol. 51, 2018, 346-351.
7
Figure: Full-state feedback system
Here, the assumption includes that the reference is equivalent to zero, i.e., = 0. Thus, the input
is, (10)
Hence, for the closed-loop feedback system the equations of state-space are,
(11)
(12)
The closed-loop feedback system’s stability as well as the time-domain performance are
evaluated especially with the help of the eigenvalues’ location in the matrix ( )that are
equivalent to the closed-loop poles. There could be three poles in the system, as both the
matrices (i.e., and ) have 3x3 matrix. By choosing an appropriate state-feedback gain
matrix , we can place these The closed-loop poles could be placed anywhere if the state-
feedback gain matrix , is selected appropriately.
The state-feedback gain, , can be found by using the MATLAB function,, because it provides
the required closed-loop poles.
9 R Bitirgen, M Hancer & I Bayezit, "All Stabilizing State Feedback Controller for Inverted Pendulum
Mechanism", in IFAC-PapersOnLine, vol. 51, 2018, 346-351.
7
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Question-7
ANSWER:
8
ANSWER:
8
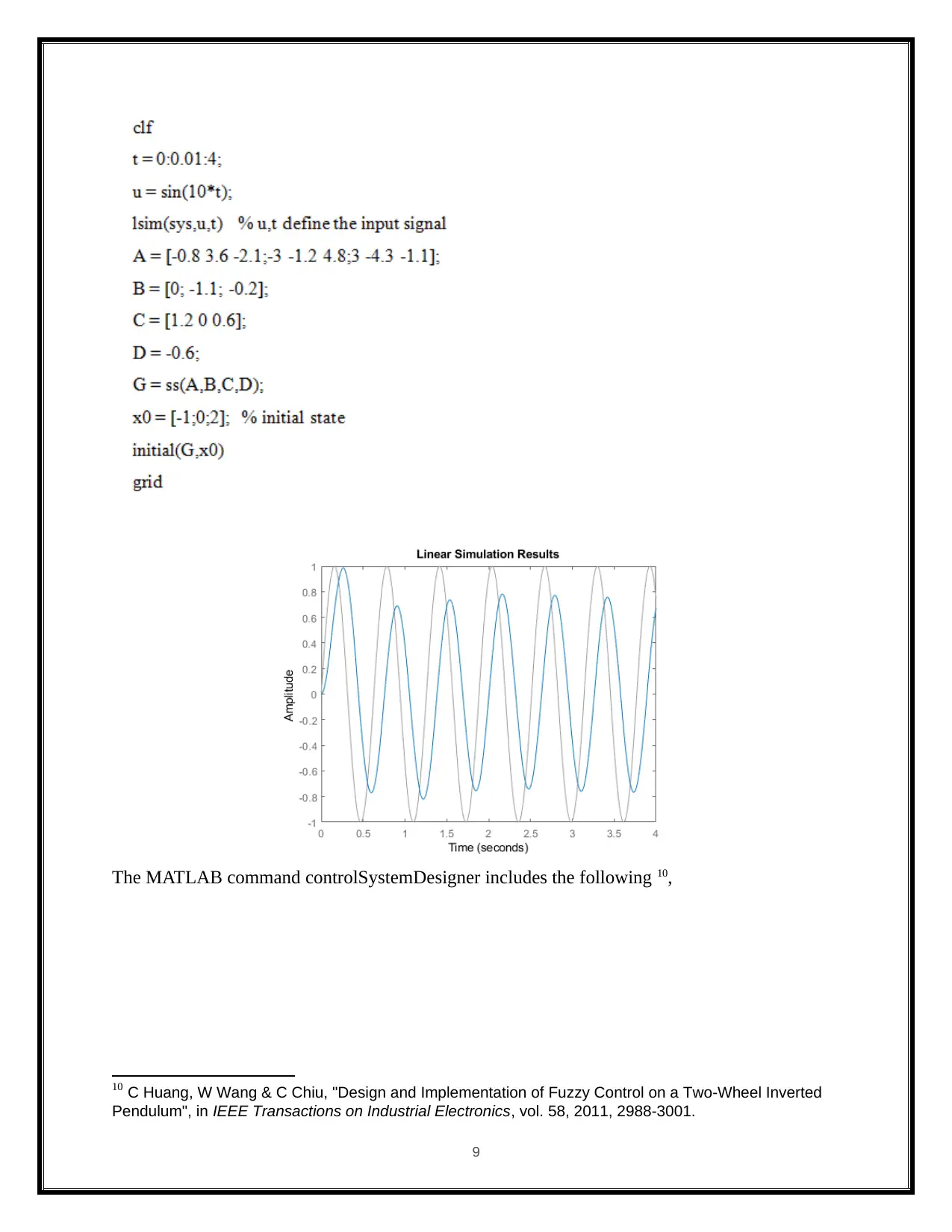
The MATLAB command controlSystemDesigner includes the following 10,
10 C Huang, W Wang & C Chiu, "Design and Implementation of Fuzzy Control on a Two-Wheel Inverted
Pendulum", in IEEE Transactions on Industrial Electronics, vol. 58, 2011, 2988-3001.
9
10 C Huang, W Wang & C Chiu, "Design and Implementation of Fuzzy Control on a Two-Wheel Inverted
Pendulum", in IEEE Transactions on Industrial Electronics, vol. 58, 2011, 2988-3001.
9

10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
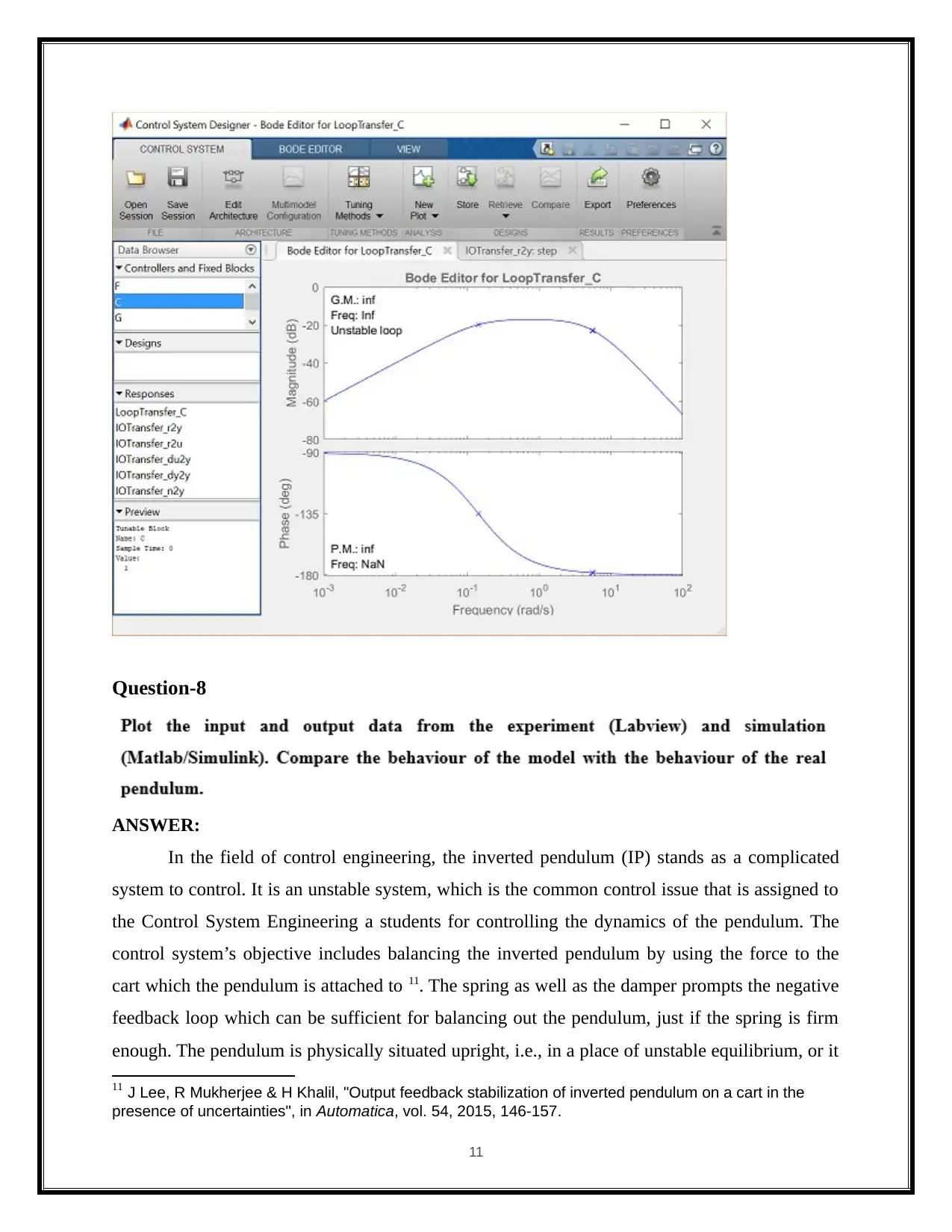
Question-8
ANSWER:
In the field of control engineering, the inverted pendulum (IP) stands as a complicated
system to control. It is an unstable system, which is the common control issue that is assigned to
the Control System Engineering a students for controlling the dynamics of the pendulum. The
control system’s objective includes balancing the inverted pendulum by using the force to the
cart which the pendulum is attached to 11. The spring as well as the damper prompts the negative
feedback loop which can be sufficient for balancing out the pendulum, just if the spring is firm
enough. The pendulum is physically situated upright, i.e., in a place of unstable equilibrium, or it
11 J Lee, R Mukherjee & H Khalil, "Output feedback stabilization of inverted pendulum on a cart in the
presence of uncertainties", in Automatica, vol. 54, 2015, 146-157.
11
ANSWER:
In the field of control engineering, the inverted pendulum (IP) stands as a complicated
system to control. It is an unstable system, which is the common control issue that is assigned to
the Control System Engineering a students for controlling the dynamics of the pendulum. The
control system’s objective includes balancing the inverted pendulum by using the force to the
cart which the pendulum is attached to 11. The spring as well as the damper prompts the negative
feedback loop which can be sufficient for balancing out the pendulum, just if the spring is firm
enough. The pendulum is physically situated upright, i.e., in a place of unstable equilibrium, or it
11 J Lee, R Mukherjee & H Khalil, "Output feedback stabilization of inverted pendulum on a cart in the
presence of uncertainties", in Automatica, vol. 54, 2015, 146-157.
11
is provided certain initial displacement. Then, the controller is changed to adjust the pendulum
and to keep up this parity within the sight of unsettling disturbances. A straightforward unsettling
influence might be a light tap on the pendulum that is balanced.
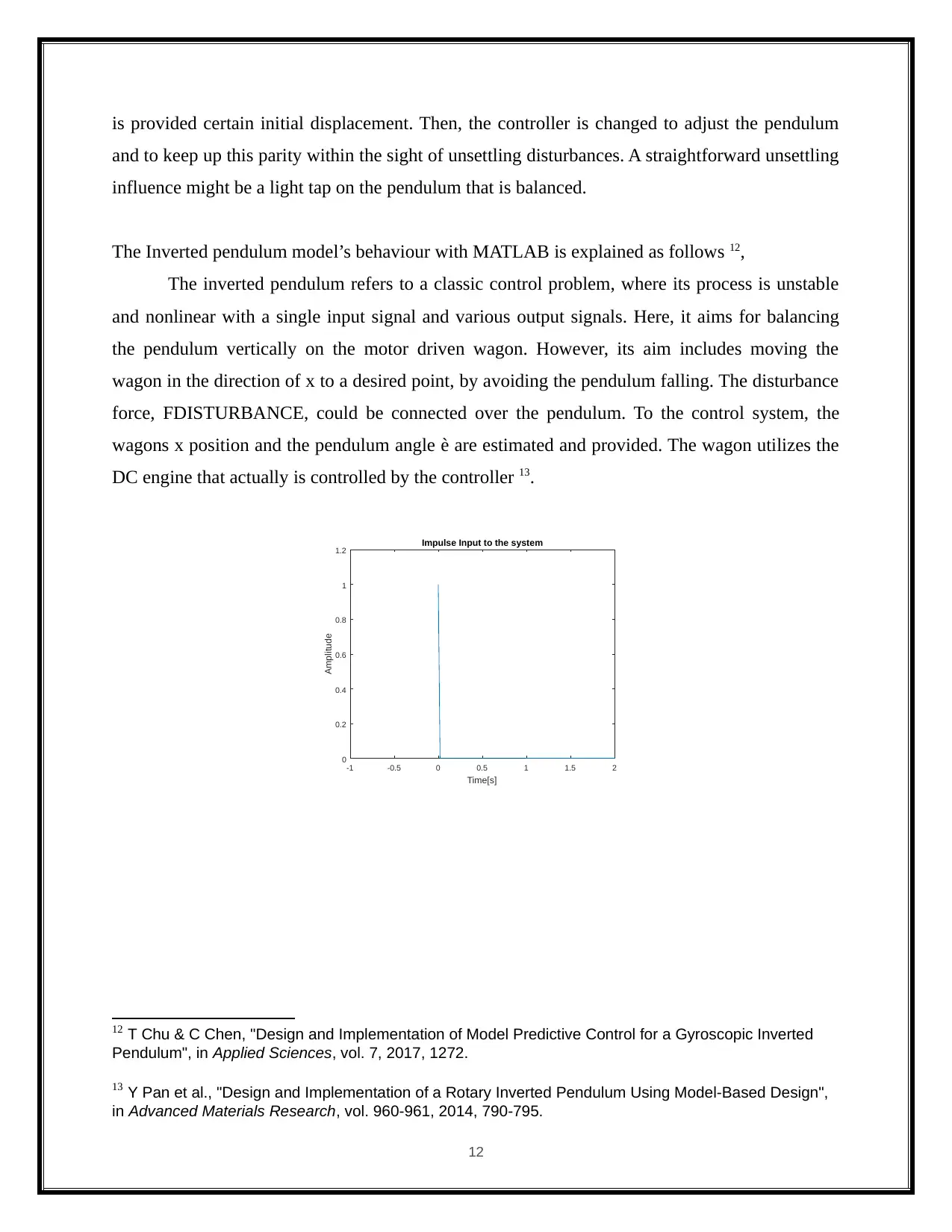
The Inverted pendulum model’s behaviour with MATLAB is explained as follows 12,
The inverted pendulum refers to a classic control problem, where its process is unstable
and nonlinear with a single input signal and various output signals. Here, it aims for balancing
the pendulum vertically on the motor driven wagon. However, its aim includes moving the
wagon in the direction of x to a desired point, by avoiding the pendulum falling. The disturbance
force, FDISTURBANCE, could be connected over the pendulum. To the control system, the
wagons x position and the pendulum angle è are estimated and provided. The wagon utilizes the
DC engine that actually is controlled by the controller 13.
Time[s]
-1 -0.5 0 0.5 1 1.5 2
Amplitude
0
0.2
0.4
0.6
0.8
1
1.2 Impulse Input to the system
12 T Chu & C Chen, "Design and Implementation of Model Predictive Control for a Gyroscopic Inverted
Pendulum", in Applied Sciences, vol. 7, 2017, 1272.
13 Y Pan et al., "Design and Implementation of a Rotary Inverted Pendulum Using Model-Based Design",
in Advanced Materials Research, vol. 960-961, 2014, 790-795.
12
and to keep up this parity within the sight of unsettling disturbances. A straightforward unsettling
influence might be a light tap on the pendulum that is balanced.
The Inverted pendulum model’s behaviour with MATLAB is explained as follows 12,
The inverted pendulum refers to a classic control problem, where its process is unstable
and nonlinear with a single input signal and various output signals. Here, it aims for balancing
the pendulum vertically on the motor driven wagon. However, its aim includes moving the
wagon in the direction of x to a desired point, by avoiding the pendulum falling. The disturbance
force, FDISTURBANCE, could be connected over the pendulum. To the control system, the
wagons x position and the pendulum angle è are estimated and provided. The wagon utilizes the
DC engine that actually is controlled by the controller 13.
Time[s]
-1 -0.5 0 0.5 1 1.5 2
Amplitude
0
0.2
0.4
0.6
0.8
1
1.2 Impulse Input to the system
12 T Chu & C Chen, "Design and Implementation of Model Predictive Control for a Gyroscopic Inverted
Pendulum", in Applied Sciences, vol. 7, 2017, 1272.
13 Y Pan et al., "Design and Implementation of a Rotary Inverted Pendulum Using Model-Based Design",
in Advanced Materials Research, vol. 960-961, 2014, 790-795.
12
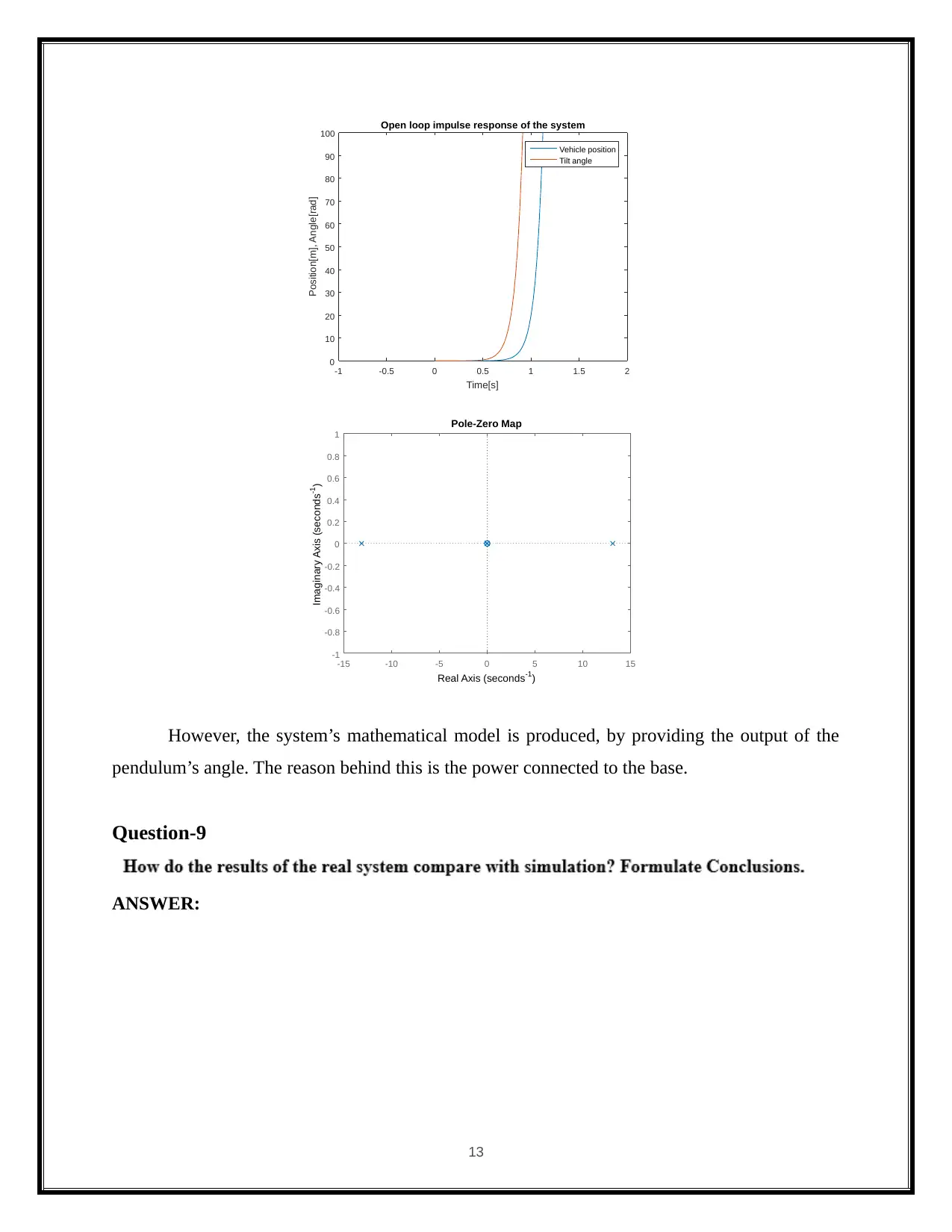
Time[s]
-1 -0.5 0 0.5 1 1.5 2
Position[m], Angle[rad]
0
10
20
30
40
50
60
70
80
90
100 Open loop impulse response of the system
Vehicle position
Tilt angle
-15 -10 -5 0 5 10 15
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
However, the system’s mathematical model is produced, by providing the output of the
pendulum’s angle. The reason behind this is the power connected to the base.
Question-9
ANSWER:
13
-1 -0.5 0 0.5 1 1.5 2
Position[m], Angle[rad]
0
10
20
30
40
50
60
70
80
90
100 Open loop impulse response of the system
Vehicle position
Tilt angle
-15 -10 -5 0 5 10 15
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Pole-Zero Map
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
However, the system’s mathematical model is produced, by providing the output of the
pendulum’s angle. The reason behind this is the power connected to the base.
Question-9
ANSWER:
13
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

The below illustrated graphs represent the comparison of θ’sreal time and simulation results 14.
14 H Li & A Lu, "The Design of Output Feedback Controller for Inverted Pendulum System", in Applied
Mechanics and Materials, vol. 336-338, 2013, 489-492.
14
14 H Li & A Lu, "The Design of Output Feedback Controller for Inverted Pendulum System", in Applied
Mechanics and Materials, vol. 336-338, 2013, 489-492.
14
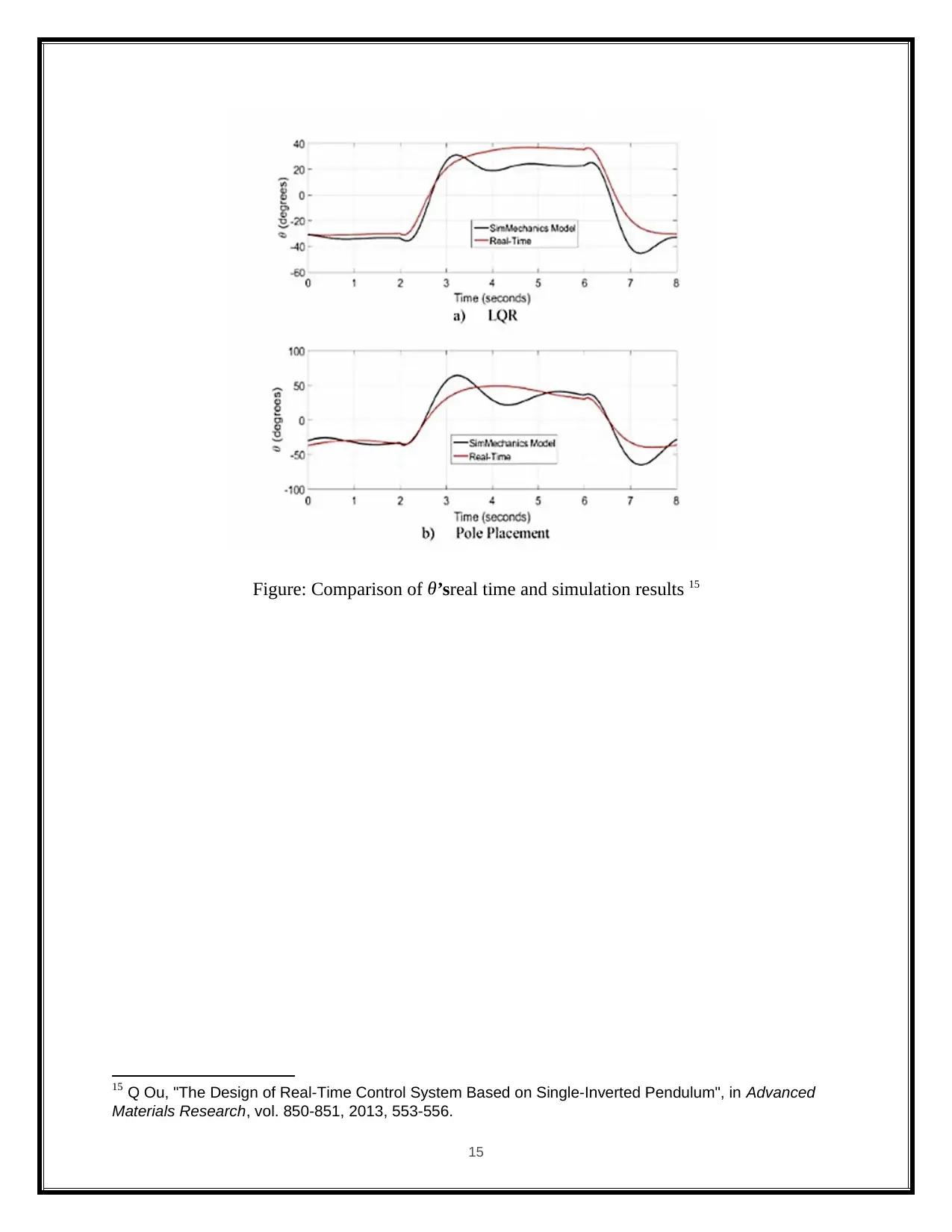
Figure: Comparison of θ’sreal time and simulation results 15
15 Q Ou, "The Design of Real-Time Control System Based on Single-Inverted Pendulum", in Advanced
Materials Research, vol. 850-851, 2013, 553-556.
15
15 Q Ou, "The Design of Real-Time Control System Based on Single-Inverted Pendulum", in Advanced
Materials Research, vol. 850-851, 2013, 553-556.
15
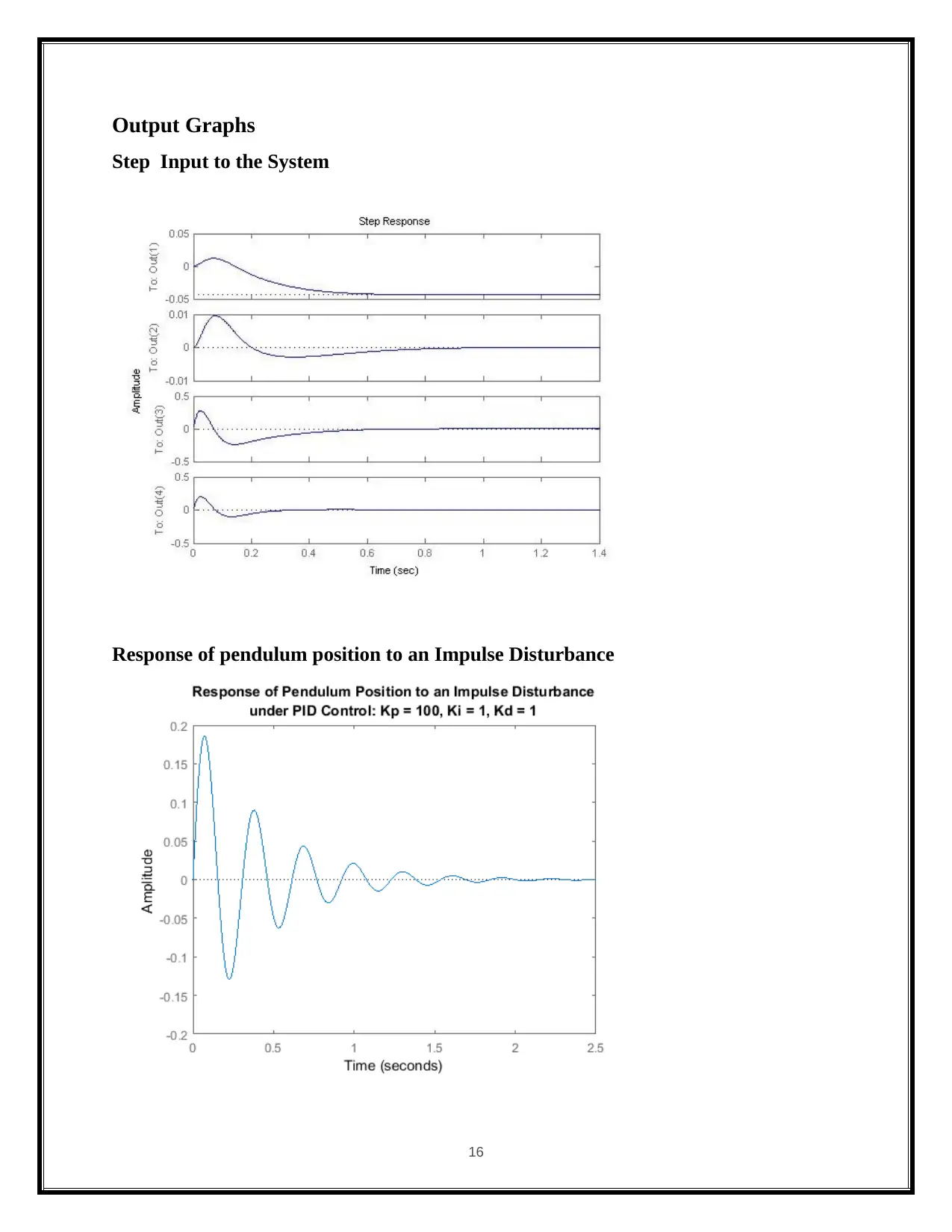
Output Graphs
Step Input to the System
Response of pendulum position to an Impulse Disturbance
16
Step Input to the System
Response of pendulum position to an Impulse Disturbance
16
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
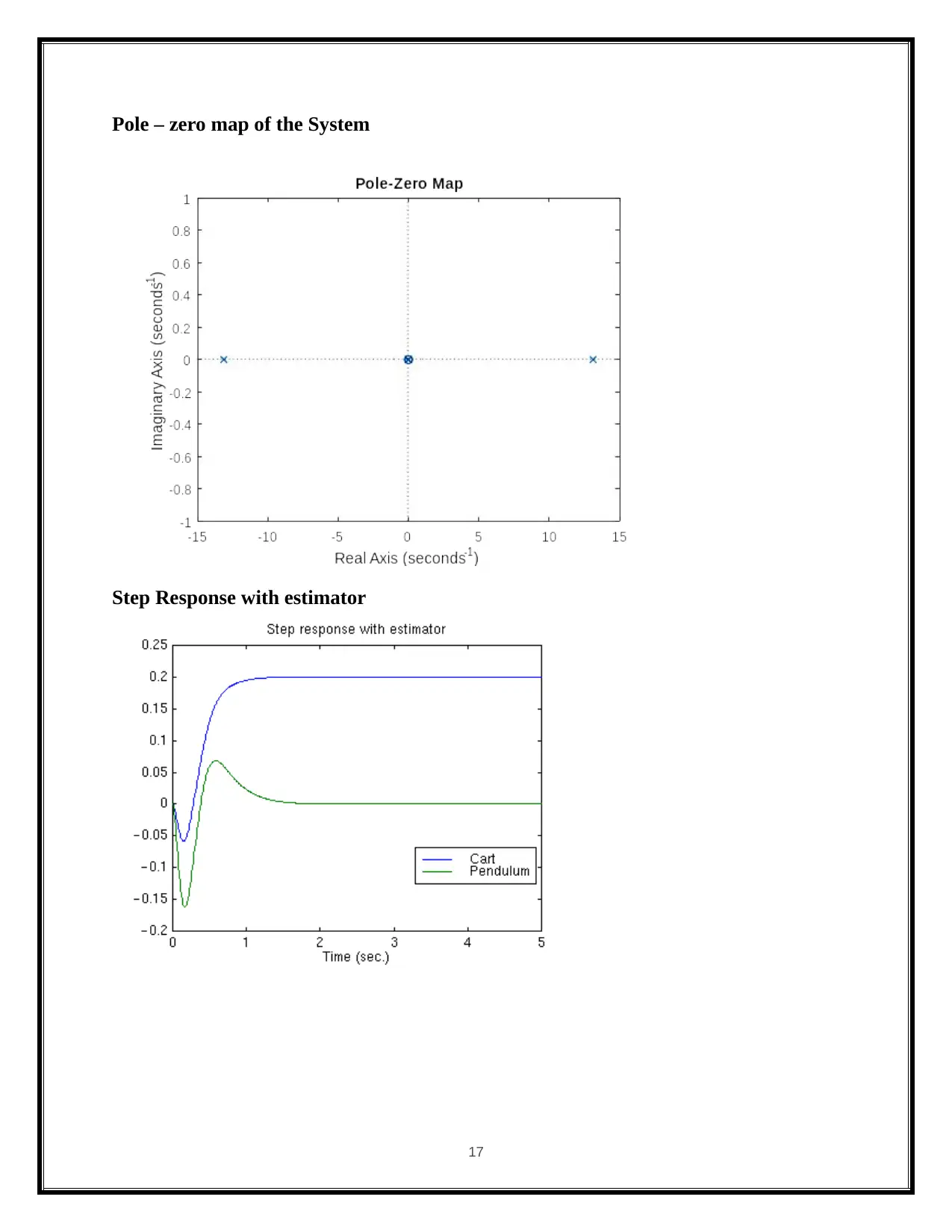
Pole – zero map of the System
Step Response with estimator
17
Step Response with estimator
17
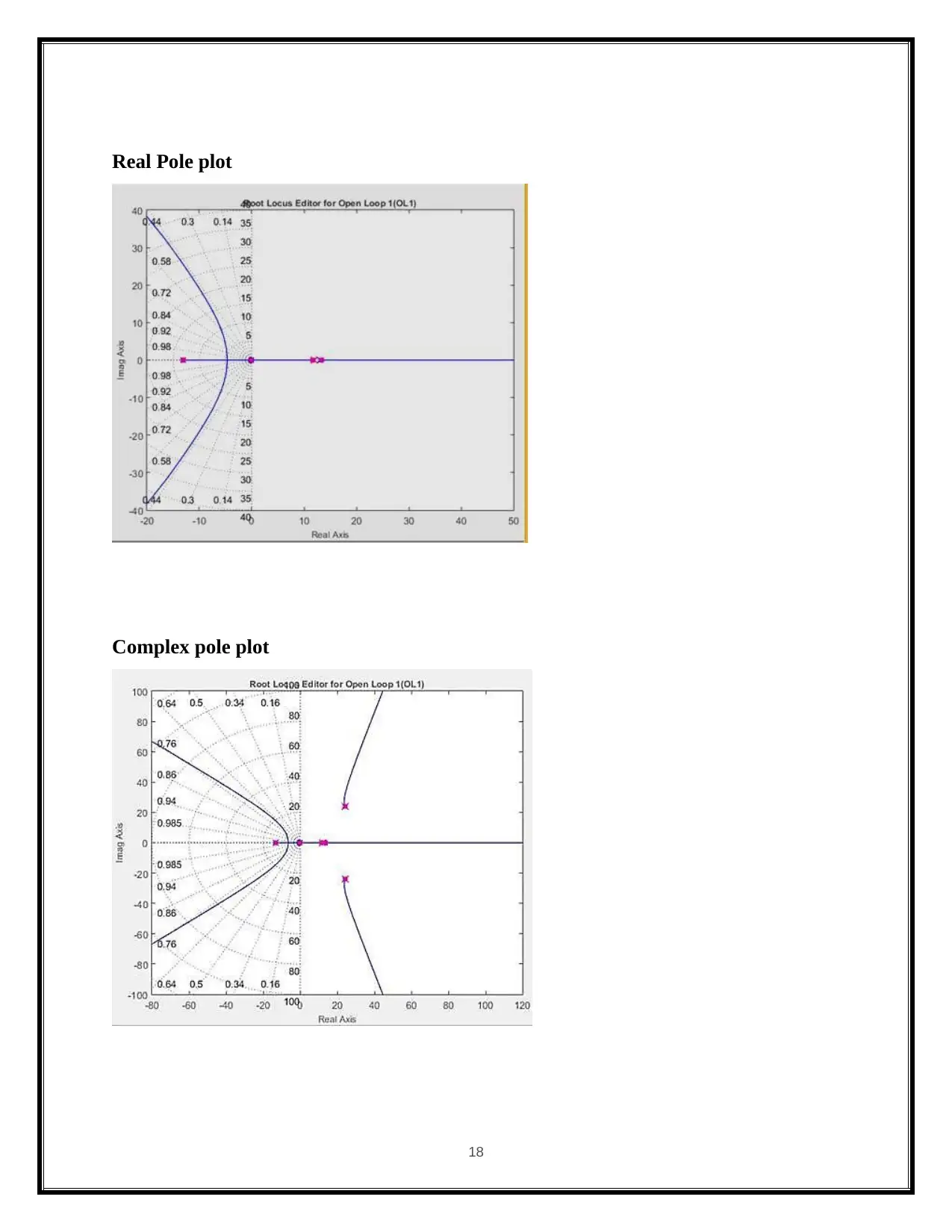
Real Pole plot
Complex pole plot
18
Complex pole plot
18
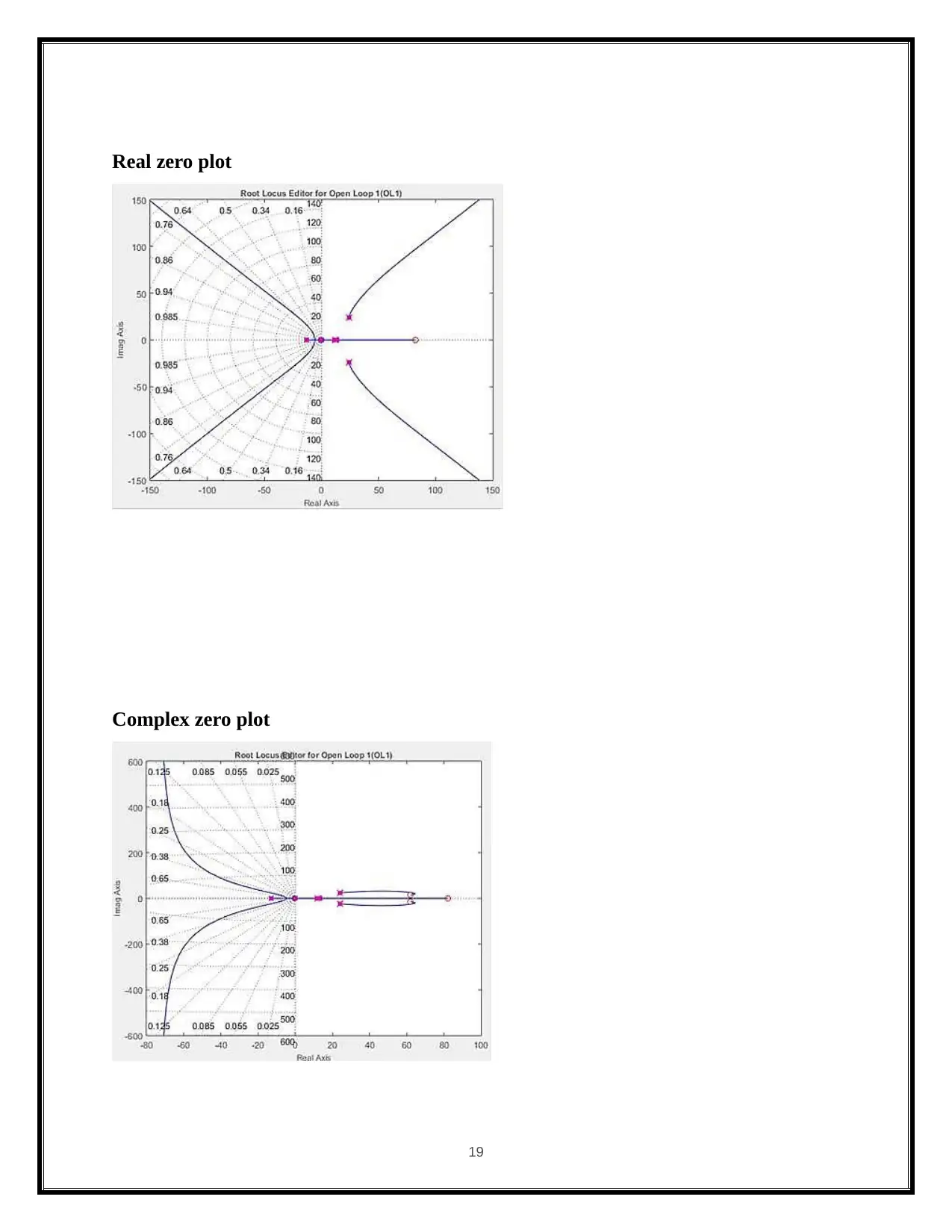
Real zero plot
Complex zero plot
19
Complex zero plot
19
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Integrator plot
20
20
Differentiator Plot
Notch filter with zero and pole plot
21
Notch filter with zero and pole plot
21
Open loop of Bode plot
Open Loop of
Nyquist
Diagram
22
Open Loop of
Nyquist
Diagram
22
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Closed Loop response of Bode and Nyquist plot
Discrete -time system response of Inverted Pendulum
23
Discrete -time system response of Inverted Pendulum
23
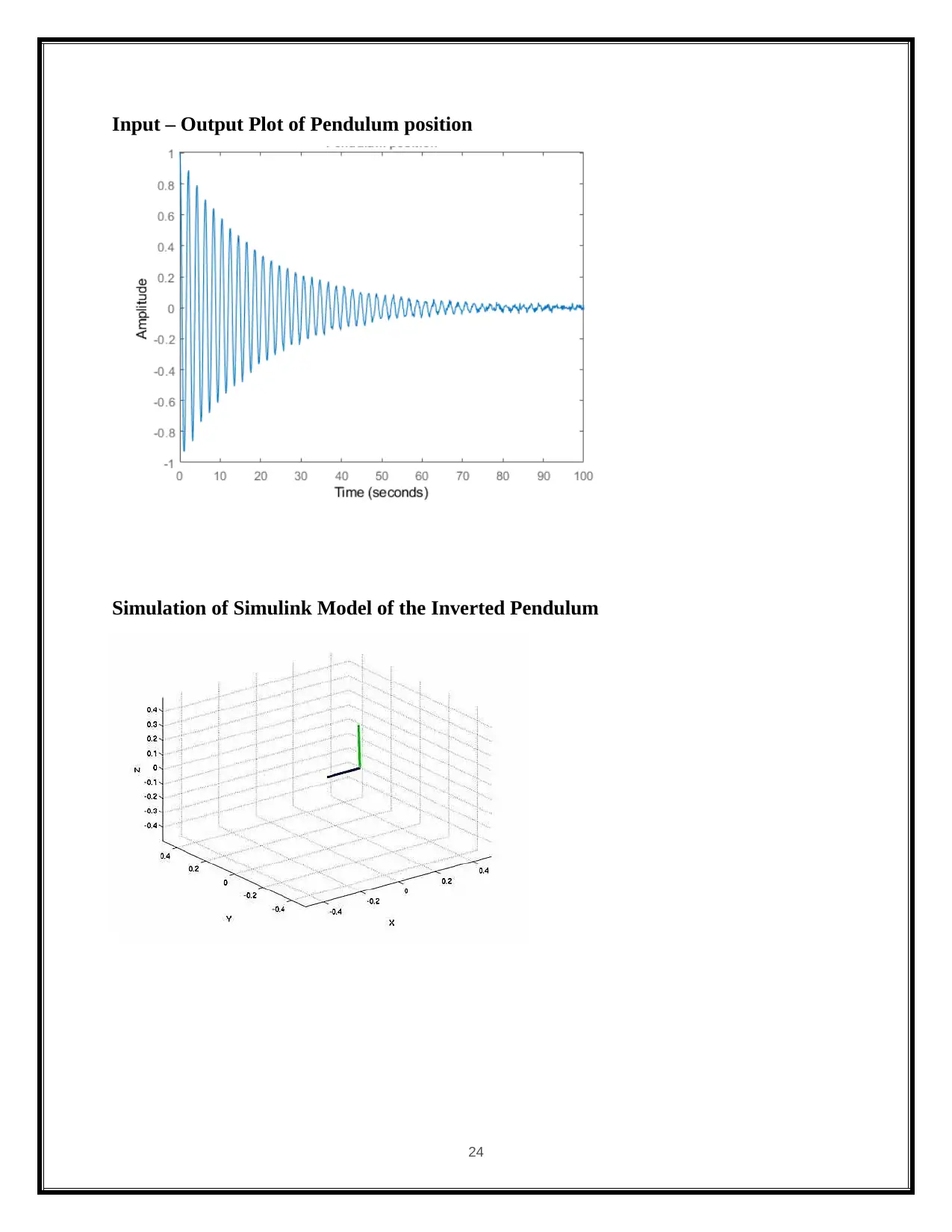
Input – Output Plot of Pendulum position
Simulation of Simulink Model of the Inverted Pendulum
24
Simulation of Simulink Model of the Inverted Pendulum
24
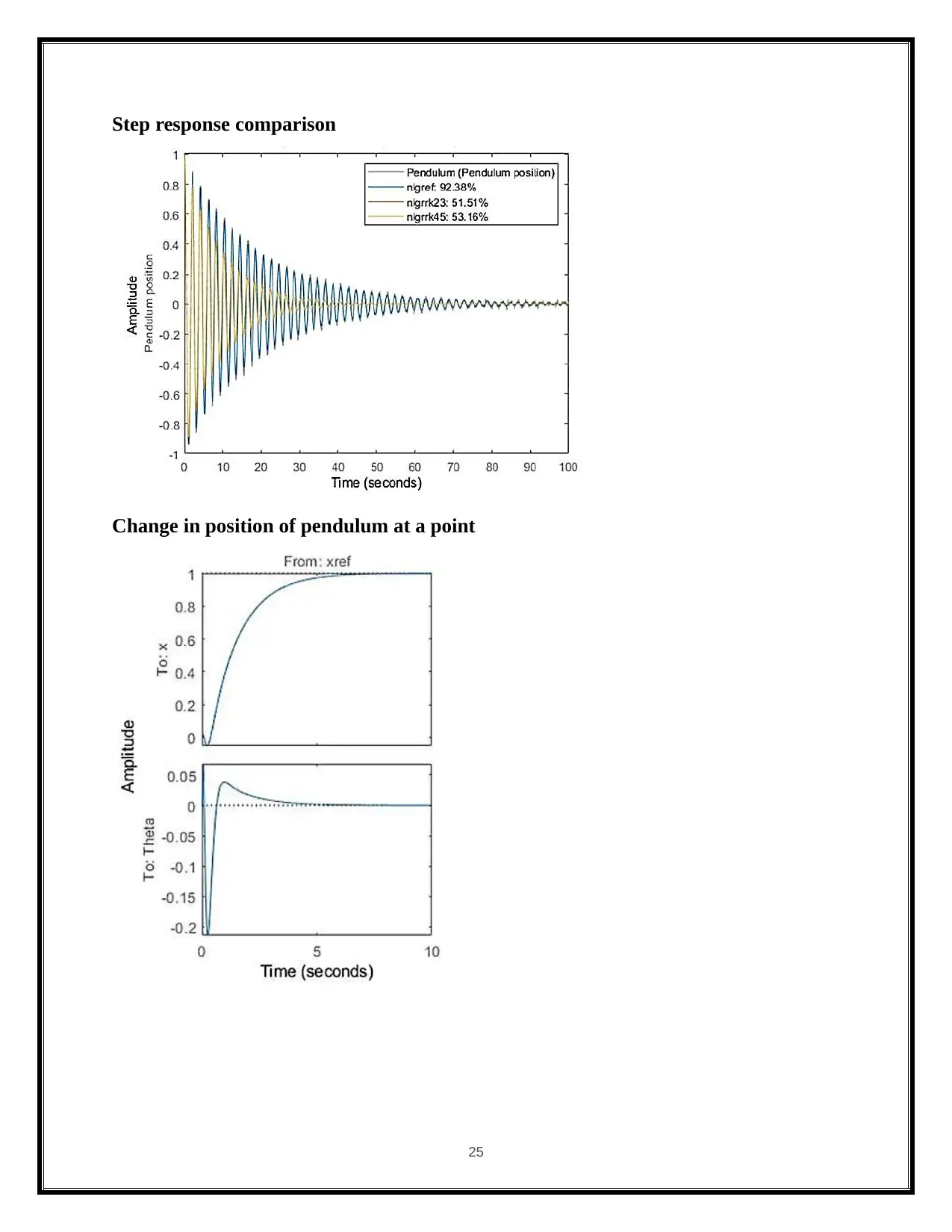
Step response comparison
Change in position of pendulum at a point
25
Change in position of pendulum at a point
25
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
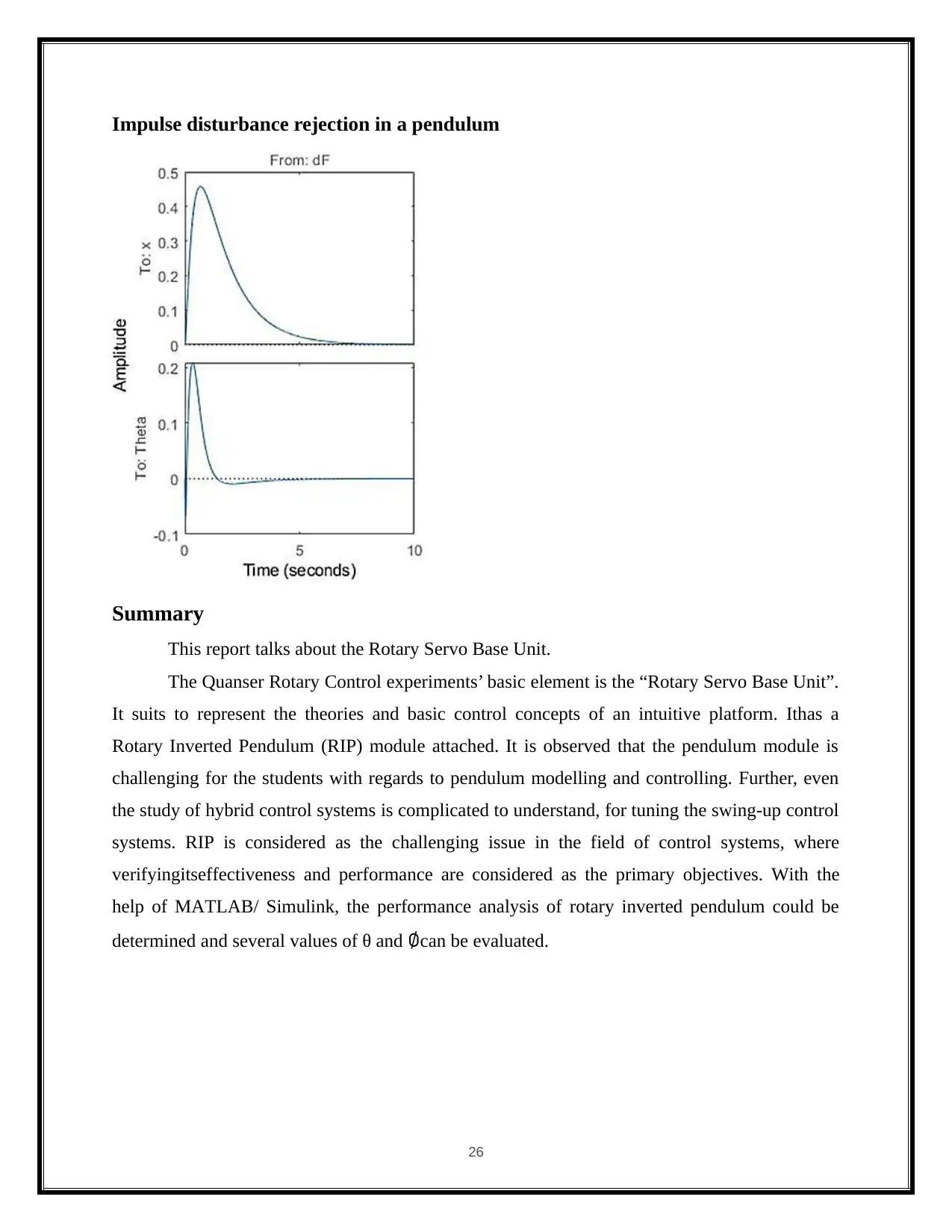
Impulse disturbance rejection in a pendulum
Summary
This report talks about the Rotary Servo Base Unit.
The Quanser Rotary Control experiments’ basic element is the “Rotary Servo Base Unit”.
It suits to represent the theories and basic control concepts of an intuitive platform. Ithas a
Rotary Inverted Pendulum (RIP) module attached. It is observed that the pendulum module is
challenging for the students with regards to pendulum modelling and controlling. Further, even
the study of hybrid control systems is complicated to understand, for tuning the swing-up control
systems. RIP is considered as the challenging issue in the field of control systems, where
verifyingitseffectiveness and performance are considered as the primary objectives. With the
help of MATLAB/ Simulink, the performance analysis of rotary inverted pendulum could be
determined and several values of θ and ∅can be evaluated.
26
Summary
This report talks about the Rotary Servo Base Unit.
The Quanser Rotary Control experiments’ basic element is the “Rotary Servo Base Unit”.
It suits to represent the theories and basic control concepts of an intuitive platform. Ithas a
Rotary Inverted Pendulum (RIP) module attached. It is observed that the pendulum module is
challenging for the students with regards to pendulum modelling and controlling. Further, even
the study of hybrid control systems is complicated to understand, for tuning the swing-up control
systems. RIP is considered as the challenging issue in the field of control systems, where
verifyingitseffectiveness and performance are considered as the primary objectives. With the
help of MATLAB/ Simulink, the performance analysis of rotary inverted pendulum could be
determined and several values of θ and ∅can be evaluated.
26

References
Aguilar-Ibáñez, C, M Suarez-Castanon, & N Cruz-Cortés, "Output feedback stabilization of the
inverted pendulum system: a Lyapunov approach.". in Nonlinear Dynamics, 70, 2012, 767-
777.
Ali, H, "Robust Stabilizing Controller Design for Inverted Pendulum System.". in Jurnal
Teknologi, 71, 2014.
Babu, J, & E Vargheese, "Stabilization of Rotary Arm Inverted Pendulum using State Feedback
Techniques.". in International Journal of Engineering Research and, V4, 2015.
Bitirgen, R, M Hancer, & I Bayezit, "All Stabilizing State Feedback Controller for Inverted
Pendulum Mechanism.". in IFAC-PapersOnLine, 51, 2018, 346-351.
Boussaada, I, I Morărescu, & S Niculescu, "Inverted pendulum stabilization: Characterization of
codimension-three triple zero bifurcation via multiple delayed proportional gains.".
in Systems & Control Letters, 82, 2015, 1-9.
Boussaada, I, I Morărescu, & S Niculescu, "Inverted Pendulum Stabilization Via a Pyragas-Type
Controller: Revisiting the Triple Zero Singularity.". in IFAC Proceedings Volumes, 47,
2014, 6806-6811.
Chu, T, & C Chen, "Design and Implementation of Model Predictive Control for a Gyroscopic
Inverted Pendulum.". in Applied Sciences, 7, 2017, 1272.
Huang, C, W Wang, & C Chiu, "Design and Implementation of Fuzzy Control on a Two-Wheel
Inverted Pendulum.". in IEEE Transactions on Industrial Electronics, 58, 2011, 2988-3001.
Lee, J, R Mukherjee, & H Khalil, "Output feedback stabilization of inverted pendulum on a cart
in the presence of uncertainties.". in Automatica, 54, 2015, 146-157.
Li, H, & A Lu, "The Design of Output Feedback Controller for Inverted Pendulum System.".
in Applied Mechanics and Materials, 336-338, 2013, 489-492.
Ou, Q, "The Design of Real-Time Control System Based on Single-Inverted Pendulum.".
in Advanced Materials Research, 850-851, 2013, 553-556.
27
Aguilar-Ibáñez, C, M Suarez-Castanon, & N Cruz-Cortés, "Output feedback stabilization of the
inverted pendulum system: a Lyapunov approach.". in Nonlinear Dynamics, 70, 2012, 767-
777.
Ali, H, "Robust Stabilizing Controller Design for Inverted Pendulum System.". in Jurnal
Teknologi, 71, 2014.
Babu, J, & E Vargheese, "Stabilization of Rotary Arm Inverted Pendulum using State Feedback
Techniques.". in International Journal of Engineering Research and, V4, 2015.
Bitirgen, R, M Hancer, & I Bayezit, "All Stabilizing State Feedback Controller for Inverted
Pendulum Mechanism.". in IFAC-PapersOnLine, 51, 2018, 346-351.
Boussaada, I, I Morărescu, & S Niculescu, "Inverted pendulum stabilization: Characterization of
codimension-three triple zero bifurcation via multiple delayed proportional gains.".
in Systems & Control Letters, 82, 2015, 1-9.
Boussaada, I, I Morărescu, & S Niculescu, "Inverted Pendulum Stabilization Via a Pyragas-Type
Controller: Revisiting the Triple Zero Singularity.". in IFAC Proceedings Volumes, 47,
2014, 6806-6811.
Chu, T, & C Chen, "Design and Implementation of Model Predictive Control for a Gyroscopic
Inverted Pendulum.". in Applied Sciences, 7, 2017, 1272.
Huang, C, W Wang, & C Chiu, "Design and Implementation of Fuzzy Control on a Two-Wheel
Inverted Pendulum.". in IEEE Transactions on Industrial Electronics, 58, 2011, 2988-3001.
Lee, J, R Mukherjee, & H Khalil, "Output feedback stabilization of inverted pendulum on a cart
in the presence of uncertainties.". in Automatica, 54, 2015, 146-157.
Li, H, & A Lu, "The Design of Output Feedback Controller for Inverted Pendulum System.".
in Applied Mechanics and Materials, 336-338, 2013, 489-492.
Ou, Q, "The Design of Real-Time Control System Based on Single-Inverted Pendulum.".
in Advanced Materials Research, 850-851, 2013, 553-556.
27

Pan, Y, P Meng, R Ge, & Z Mao, "Design and Implementation of a Rotary Inverted Pendulum
Using Model-Based Design.". in Advanced Materials Research, 960-961, 2014, 790-795.
S A, P, "THE STABILIZATION OF FORCED INVERTED PENDULUM VIA FUZZY
CONTROLLER.". in International Journal of Research in Engineering and Technology, 05,
2016, 152-155.
Wan, L, J Lei, & H Wu, "Design of LQR Controller for the Inverted Pendulum.". in Advanced
Materials Research, 1037, 2014, 221-224.
Zhang, B, & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted
Pendulum.". in Advanced Materials Research, 187, 2011, 548-553.
28
Using Model-Based Design.". in Advanced Materials Research, 960-961, 2014, 790-795.
S A, P, "THE STABILIZATION OF FORCED INVERTED PENDULUM VIA FUZZY
CONTROLLER.". in International Journal of Research in Engineering and Technology, 05,
2016, 152-155.
Wan, L, J Lei, & H Wu, "Design of LQR Controller for the Inverted Pendulum.". in Advanced
Materials Research, 1037, 2014, 221-224.
Zhang, B, & L Gu, "Robust Control Design and Simulation for Cantilever-Typed Inverted
Pendulum.". in Advanced Materials Research, 187, 2011, 548-553.
28
1 out of 31
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





