ITC544 Computer Organization and Architecture: Solved Assignment

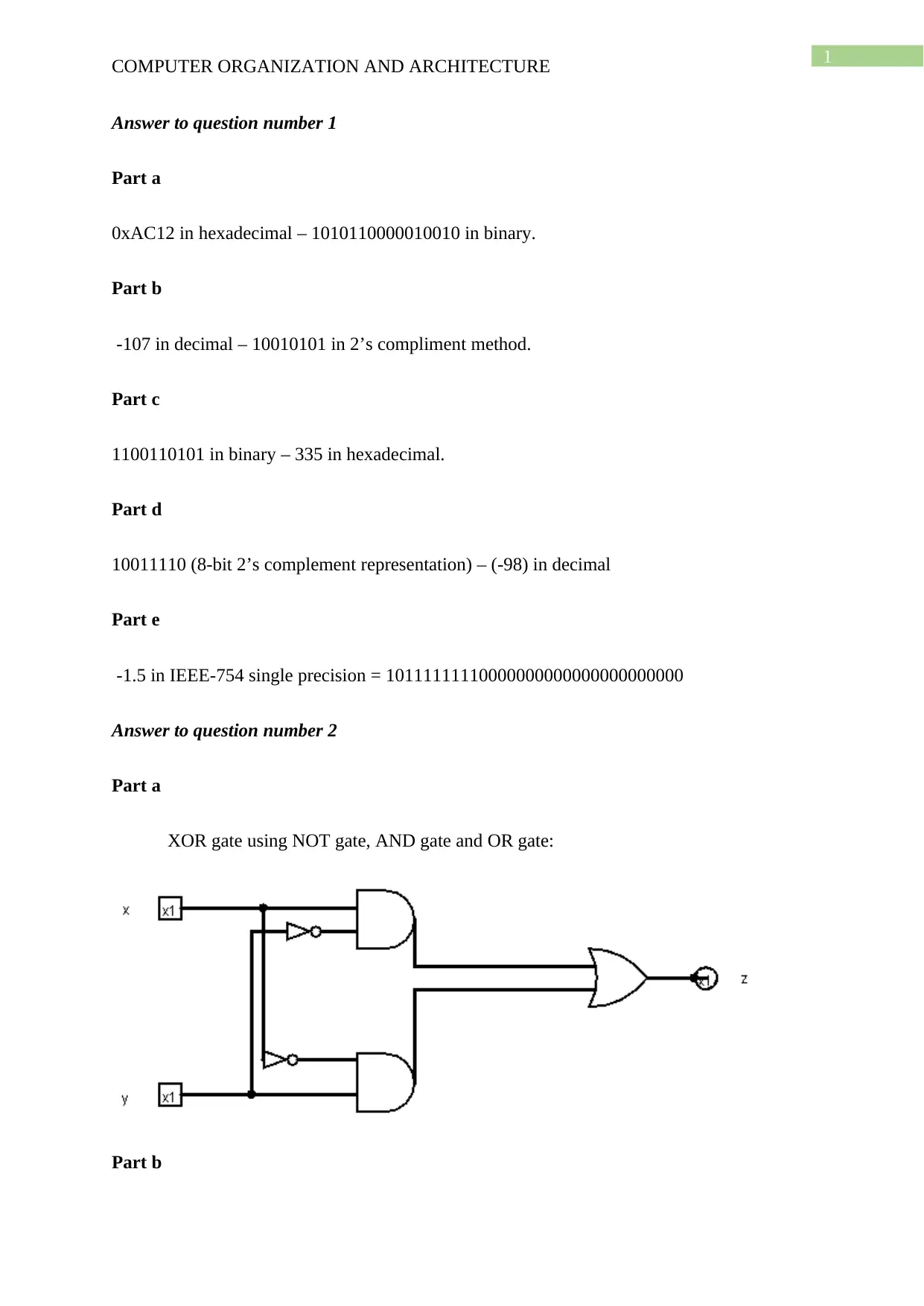
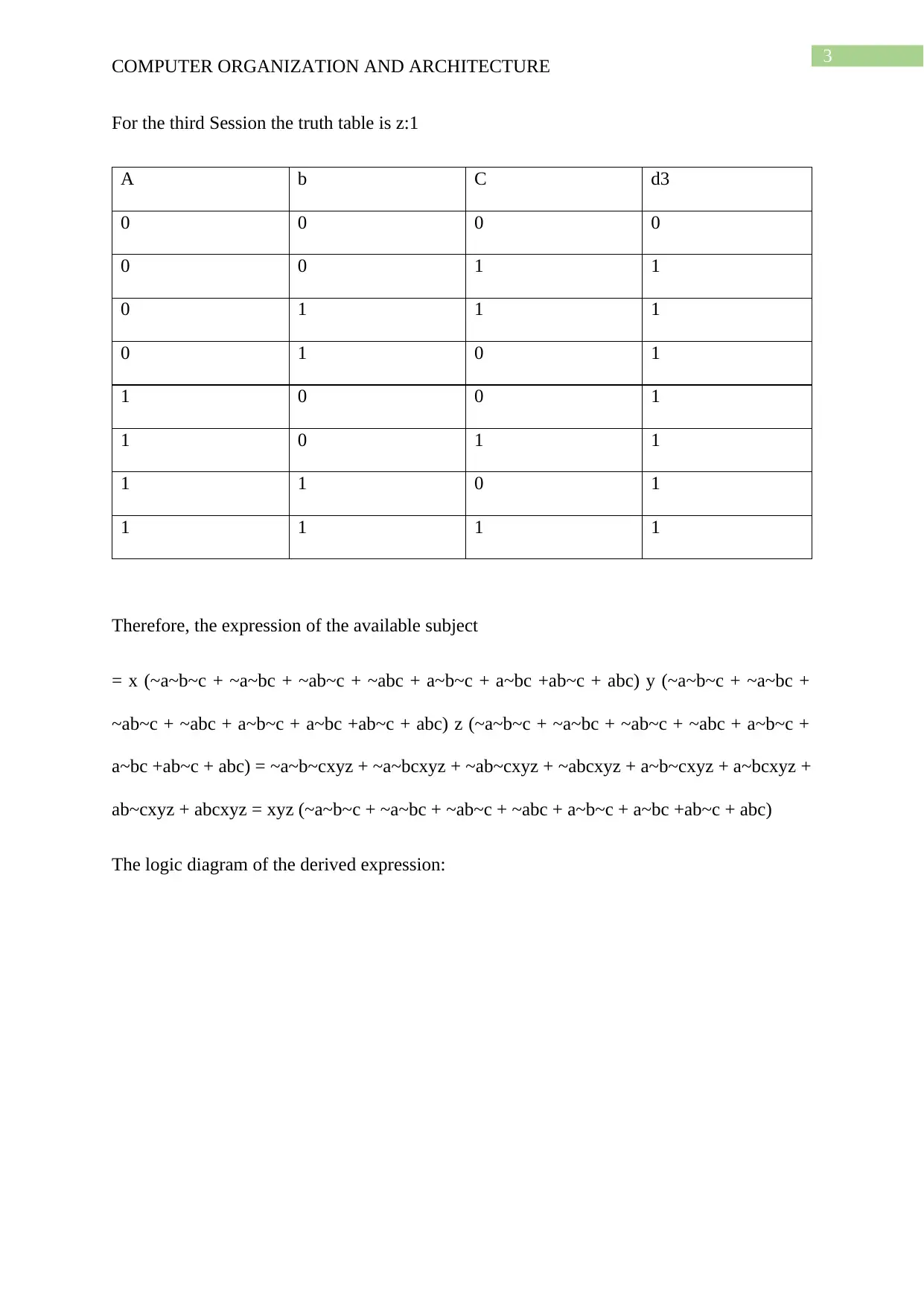
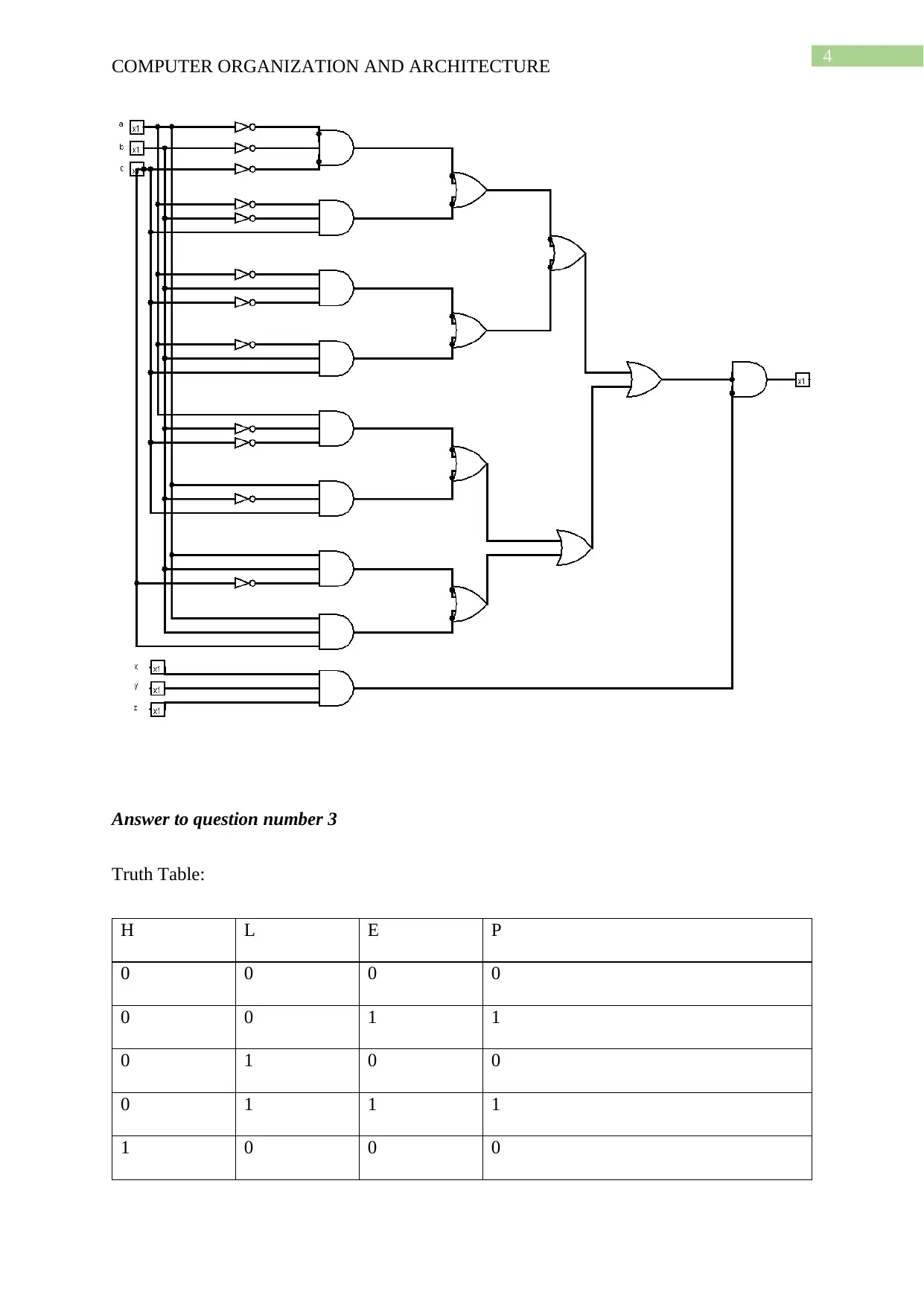
This document provides a solved assignment for a Computer Organization and Architecture course, likely ITC544. It includes solutions to problems involving data representation, such as converting between hexadecimal, binary, and decimal formats, as well as 2's complement representation and IEEE-754 single-precision floating-point representation. The assignment also covers digital logic, including the implementation of an XOR gate using other basic gates and the creation of truth tables and logical expressions for given scenarios. The document concludes with a bibliography referencing relevant academic resources. Desklib provides a platform to explore similar solved assignments and past papers.

Running head: COMPUTER ORGANIZATION AND ARCHITECTURE
Computer Organization and Architecture
Name of the Student:
Name of the University:
Author Note

1
COMPUTER ORGANIZATION AND ARCHITECTURE
Answer to question number 1
Part a
0xAC12 in hexadecimal – 1010110000010010 in binary.
Part b
-107 in decimal – 10010101 in 2’s compliment method.
Part c
1100110101 in binary – 335 in hexadecimal.
Part d
10011110 (8-bit 2’s complement representation) – (-98) in decimal
Part e
-1.5 in IEEE-754 single precision = 10111111110000000000000000000000
Answer to question number 2
Part a
XOR gate using NOT gate, AND gate and OR gate:
Part b

2
COMPUTER ORGANIZATION AND ARCHITECTURE
Let the three subjects that the student can apply be a, b and c and the three sessions be x, y
and z.
For the first session truth table is x: 1
a b C d1
0 0 0 0
0 0 1 1
0 1 1 1
0 1 0 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
For the second session the truth table is y:1
a b C d2
0 0 0 0
0 0 1 1
0 1 1 1
0 1 0 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1

3
COMPUTER ORGANIZATION AND ARCHITECTURE
For the third Session the truth table is z:1
A b C d3
0 0 0 0
0 0 1 1
0 1 1 1
0 1 0 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Therefore, the expression of the available subject
= x (~a~b~c + ~a~bc + ~ab~c + ~abc + a~b~c + a~bc +ab~c + abc) y (~a~b~c + ~a~bc +
~ab~c + ~abc + a~b~c + a~bc +ab~c + abc) z (~a~b~c + ~a~bc + ~ab~c + ~abc + a~b~c +
a~bc +ab~c + abc) = ~a~b~cxyz + ~a~bcxyz + ~ab~cxyz + ~abcxyz + a~b~cxyz + a~bcxyz +
ab~cxyz + abcxyz = xyz (~a~b~c + ~a~bc + ~ab~c + ~abc + a~b~c + a~bc +ab~c + abc)
The logic diagram of the derived expression:

4
COMPUTER ORGANIZATION AND ARCHITECTURE
Answer to question number 3
Truth Table:
H L E P
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0

5
COMPUTER ORGANIZATION AND ARCHITECTURE
1 0 1 1
1 1 0 0
1 1 1 1
The expression of the logical diagram:
P = ((H’L + HL’). E) + (H.L)
= EH’L + H’LE + HL

6
COMPUTER ORGANIZATION AND ARCHITECTURE
Bibliography
Chattopadhyay, A., Amarú, L., Soeken, M., Gaillardon, P. E., & De Micheli, G. (2016, May).
Notes on majority Boolean algebra. In Multiple-Valued Logic (ISMVL), 2016 IEEE
46th International Symposium on (pp. 50-55). IEEE.
Smessaert, H., & Demey, L. (2016, August). Visualising the Boolean Algebra $$\mathbb {B}
_ {4} $$ in 3D. In International Conference on Theory and Application of Diagrams
(pp. 289-292). Springer, Cham.