Analysis of Statistical Data: MATH 1P98 Practical Assignment 1
VerifiedAdded on 2020/04/07
|15
|867
|302
Homework Assignment
AI Summary
This document provides a detailed solution to a MATH 1P98 Practical Statistics assignment. It includes a frequency distribution table and histogram analysis for length data, calculating percentages, and identifying outliers. The assignment further computes mean, median, and mode for firefighter fatality data and assesses the normality of the distribution. It also addresses Z-scores, percentiles, and the application of the empirical rule and Chebyshev's theorem. Additionally, the solution covers the five-number summary, box plots, and analysis of stock price volatility, including calculations of mean, median, and standard deviation. The document offers comprehensive statistical analysis and data interpretation.

MATH 1P98 – PRACTICAL STATISTICS
Assignment: 1
STUDENT ID/ NAME
[Pick the date]
Assignment: 1
STUDENT ID/ NAME
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 1
(a) Frequency distribution table for length data
(b) Percentage of observation greater than 60.4 units ¿ ?
Total number of observation = 54
Observation greater than 60.4 units = 28
Percentage of observation greater than 60.4 units = 28/54 = 51.85%
1
(a) Frequency distribution table for length data
(b) Percentage of observation greater than 60.4 units ¿ ?
Total number of observation = 54
Observation greater than 60.4 units = 28
Percentage of observation greater than 60.4 units = 28/54 = 51.85%
1
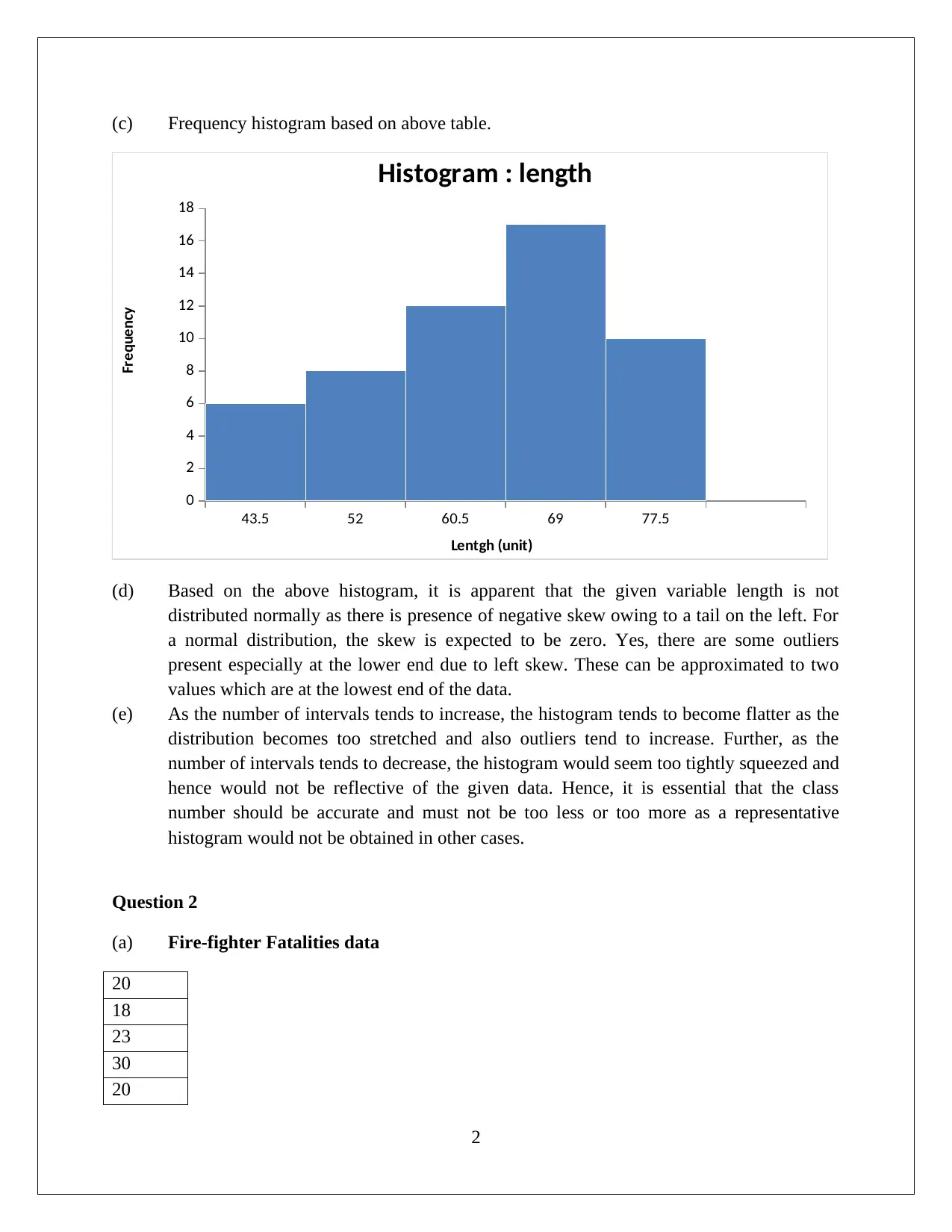
(c) Frequency histogram based on above table.
43.5 52 60.5 69 77.5
0
2
4
6
8
10
12
14
16
18
Histogram : length
Lentgh (unit)
Frequency
(d) Based on the above histogram, it is apparent that the given variable length is not
distributed normally as there is presence of negative skew owing to a tail on the left. For
a normal distribution, the skew is expected to be zero. Yes, there are some outliers
present especially at the lower end due to left skew. These can be approximated to two
values which are at the lowest end of the data.
(e) As the number of intervals tends to increase, the histogram tends to become flatter as the
distribution becomes too stretched and also outliers tend to increase. Further, as the
number of intervals tends to decrease, the histogram would seem too tightly squeezed and
hence would not be reflective of the given data. Hence, it is essential that the class
number should be accurate and must not be too less or too more as a representative
histogram would not be obtained in other cases.
Question 2
(a) Fire-fighter Fatalities data
20
18
23
30
20
2
43.5 52 60.5 69 77.5
0
2
4
6
8
10
12
14
16
18
Histogram : length
Lentgh (unit)
Frequency
(d) Based on the above histogram, it is apparent that the given variable length is not
distributed normally as there is presence of negative skew owing to a tail on the left. For
a normal distribution, the skew is expected to be zero. Yes, there are some outliers
present especially at the lower end due to left skew. These can be approximated to two
values which are at the lowest end of the data.
(e) As the number of intervals tends to increase, the histogram tends to become flatter as the
distribution becomes too stretched and also outliers tend to increase. Further, as the
number of intervals tends to decrease, the histogram would seem too tightly squeezed and
hence would not be reflective of the given data. Hence, it is essential that the class
number should be accurate and must not be too less or too more as a representative
histogram would not be obtained in other cases.
Question 2
(a) Fire-fighter Fatalities data
20
18
23
30
20
2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

12
24
9
25
15
8
11
15
34
Computation of mean
∑ xi= ( 20+18+23+30+20+ 12+ 24+9+ 25+15+8+11+15+34 )
∑ xi=264
Number of observation n=14
Mean ¿ ∑ xi
n = ( 264
14 )=18.85
Computation of median
The data can be r-arranged from lower to upper order as
8
9
11
12
15
15
18
20
20
23
24
25
30
3
24
9
25
15
8
11
15
34
Computation of mean
∑ xi= ( 20+18+23+30+20+ 12+ 24+9+ 25+15+8+11+15+34 )
∑ xi=264
Number of observation n=14
Mean ¿ ∑ xi
n = ( 264
14 )=18.85
Computation of median
The data can be r-arranged from lower to upper order as
8
9
11
12
15
15
18
20
20
23
24
25
30
3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

34
It is apparent that number of observation is even and hence the median would be average of two
middle terms (7th term and 8th term).
Median = (18+20)/2 = 19
Computation of mode
Highest frequency value is 20 with frequency of 2 and hence, the mode would be 20.
As the measures of the central tendency (mean, median and mode) do not converge to a single
value, hence the given distribution would not be normal.
(b) Variance and standard deviation of the data
Mean of data x=18.85
x (x−x ) (x−x )2
20 1.14 1.31
18 -0.86 0.73
23 4.14 17.16
30 11.14 124.16
20 1.14 1.31
12 -6.86 47.02
24 5.14 26.45
9 -9.86 97.16
25 6.14 37.73
15 -3.86 14.88
8 -10.86 117.88
11 -7.86 61.73
15 -3.86 14.88
34 15.14 229.31
Total 0.00 791.71
4
It is apparent that number of observation is even and hence the median would be average of two
middle terms (7th term and 8th term).
Median = (18+20)/2 = 19
Computation of mode
Highest frequency value is 20 with frequency of 2 and hence, the mode would be 20.
As the measures of the central tendency (mean, median and mode) do not converge to a single
value, hence the given distribution would not be normal.
(b) Variance and standard deviation of the data
Mean of data x=18.85
x (x−x ) (x−x )2
20 1.14 1.31
18 -0.86 0.73
23 4.14 17.16
30 11.14 124.16
20 1.14 1.31
12 -6.86 47.02
24 5.14 26.45
9 -9.86 97.16
25 6.14 37.73
15 -3.86 14.88
8 -10.86 117.88
11 -7.86 61.73
15 -3.86 14.88
34 15.14 229.31
Total 0.00 791.71
4

Standard deviation s2= √ ∑ ( x−x)2
n−1 =¿ √ 791.71
14−1 =¿ 7.8039 ¿ ¿
Variance s=(7.8039)2=60.9011
∑ (x−x )=0.00
The above is equal to zero as it highlights the sum of deviations from the mean which for all data
set is always zero.
(c) The standard deviation would increase since there would be additional deviation from the
mean which would increase the overall numerator and hence lead to a higher value of
standard deviation despite the increase in values.
Question 3
(a) Percentage of car lengths falls between 144 and 234 ¿ ?
x=189
s=15
P ( 144< X <234 ) =P ( 144−189< X−x <234−189 )
5
n−1 =¿ √ 791.71
14−1 =¿ 7.8039 ¿ ¿
Variance s=(7.8039)2=60.9011
∑ (x−x )=0.00
The above is equal to zero as it highlights the sum of deviations from the mean which for all data
set is always zero.
(c) The standard deviation would increase since there would be additional deviation from the
mean which would increase the overall numerator and hence lead to a higher value of
standard deviation despite the increase in values.
Question 3
(a) Percentage of car lengths falls between 144 and 234 ¿ ?
x=189
s=15
P ( 144< X <234 ) =P ( 144−189< X−x <234−189 )
5
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
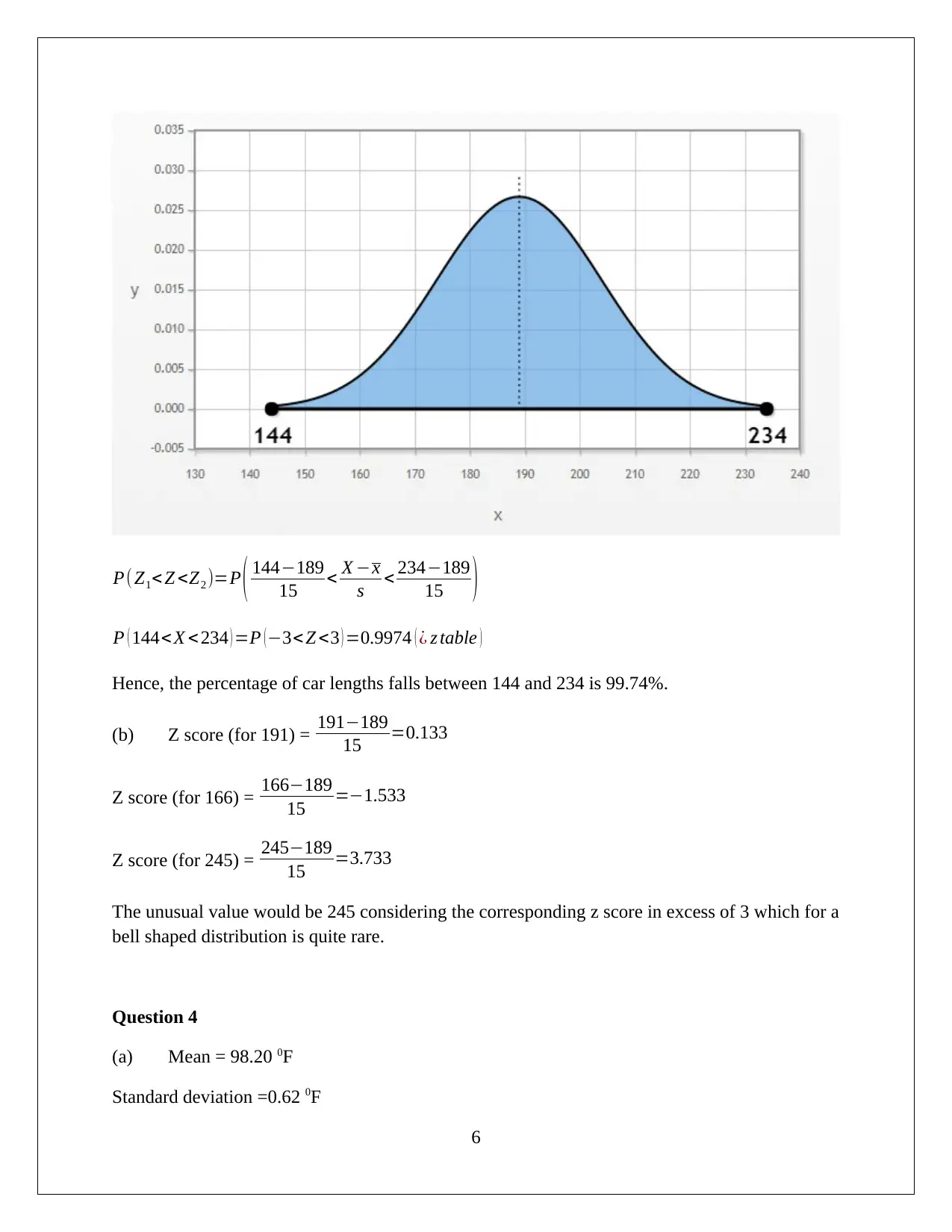
P(Z1< Z <Z2 )=P ( 144−189
15 < X −x
s < 234−189
15 )
P ( 144< X <234 ) =P (−3< Z <3 ) =0.9974 ( ¿ z table )
Hence, the percentage of car lengths falls between 144 and 234 is 99.74%.
(b) Z score (for 191) = 191−189
15 =0.133
Z score (for 166) = 166−189
15 =−1.533
Z score (for 245) = 245−189
15 =3.733
The unusual value would be 245 considering the corresponding z score in excess of 3 which for a
bell shaped distribution is quite rare.
Question 4
(a) Mean = 98.20 0F
Standard deviation =0.62 0F
6
15 < X −x
s < 234−189
15 )
P ( 144< X <234 ) =P (−3< Z <3 ) =0.9974 ( ¿ z table )
Hence, the percentage of car lengths falls between 144 and 234 is 99.74%.
(b) Z score (for 191) = 191−189
15 =0.133
Z score (for 166) = 166−189
15 =−1.533
Z score (for 245) = 245−189
15 =3.733
The unusual value would be 245 considering the corresponding z score in excess of 3 which for a
bell shaped distribution is quite rare.
Question 4
(a) Mean = 98.20 0F
Standard deviation =0.62 0F
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Body temperatures that are 2.5 of standard deviation =?
Percentage of body temperature fall in this range =?
Body temperature
98.6 96.6 98 98 99 97.4 98.4 98.4 98.4 98.6
Lower limit ¿ 98.20− ( 2.5∗0.62 )=96.65
Upper limit =98.20+ (2.5∗0.62 ) =99.75
Body temperatures which fall between these two limits are shown below:
97.4 98 98 98.4 98.4 98.4 98.6 98.6 99
Percentage of body temperature fall in this range = (9/10)*100 = 90%
b) It would not be reasonable to use the empirical rule for the Length data as it is not normally
distributed as has been earlier highlighted. The empirical rule can only be applied for those
distributions which are near normal and have a bell shaped curve. However, it would be
reasonable to apply the Chebyshev theorem for the Length data as this theorem is valid for non-
normal distributions as well.
Question 5
(a) The data value 69.9 would lie in the 80th percentile of the given data considering the fact
that only 10 values in the length data would be greater than this value. The interpretation
of this length with regards to bear length is that 80% of the bears would have a length
lesser than 69.9
(b) Computation of percentile
L= ( K
100 )N
Where,
k = percentile
7
Percentage of body temperature fall in this range =?
Body temperature
98.6 96.6 98 98 99 97.4 98.4 98.4 98.4 98.6
Lower limit ¿ 98.20− ( 2.5∗0.62 )=96.65
Upper limit =98.20+ (2.5∗0.62 ) =99.75
Body temperatures which fall between these two limits are shown below:
97.4 98 98 98.4 98.4 98.4 98.6 98.6 99
Percentage of body temperature fall in this range = (9/10)*100 = 90%
b) It would not be reasonable to use the empirical rule for the Length data as it is not normally
distributed as has been earlier highlighted. The empirical rule can only be applied for those
distributions which are near normal and have a bell shaped curve. However, it would be
reasonable to apply the Chebyshev theorem for the Length data as this theorem is valid for non-
normal distributions as well.
Question 5
(a) The data value 69.9 would lie in the 80th percentile of the given data considering the fact
that only 10 values in the length data would be greater than this value. The interpretation
of this length with regards to bear length is that 80% of the bears would have a length
lesser than 69.9
(b) Computation of percentile
L= ( K
100 )N
Where,
k = percentile
7

n=number of values
Arrange the data into ascending order
8
Arrange the data into ascending order
8
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

P20
L= ( 20
100 )∗54=10.8 11
Hence, P20 would be 11th term of the data set i. e 48.0
P72
L= ( 72
100 )∗54=38.88 39
Hence, P20 would be 39th term of the dataset i. e 65.0
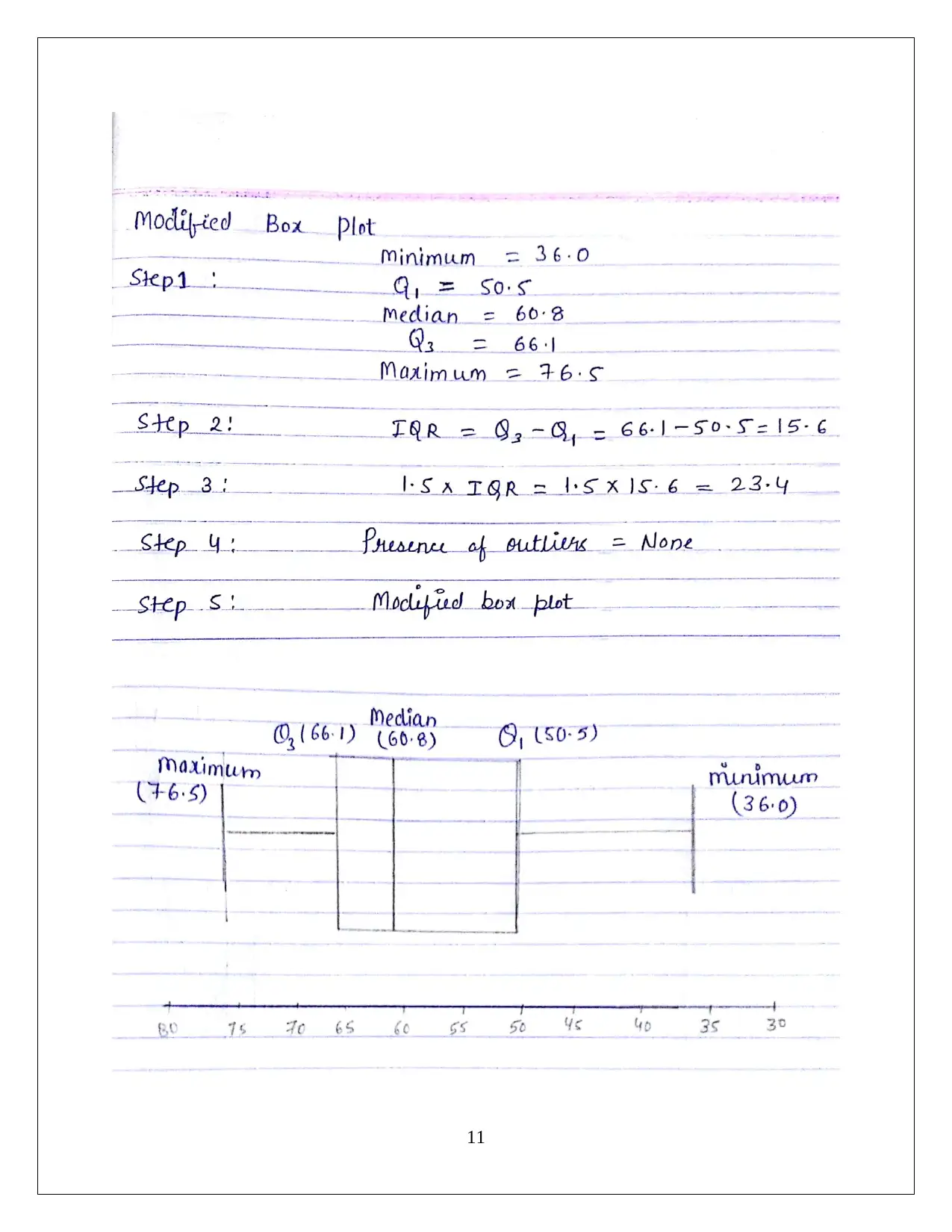
(c) 5 –number summary for the data
Box Plot
10
L= ( 20
100 )∗54=10.8 11
Hence, P20 would be 11th term of the data set i. e 48.0
P72
L= ( 72
100 )∗54=38.88 39
Hence, P20 would be 39th term of the dataset i. e 65.0
(c) 5 –number summary for the data
Box Plot
10
11
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





