Confidence Interval for Proportion and Mean of Kuku on Marlborough Sounds Mussel Farm

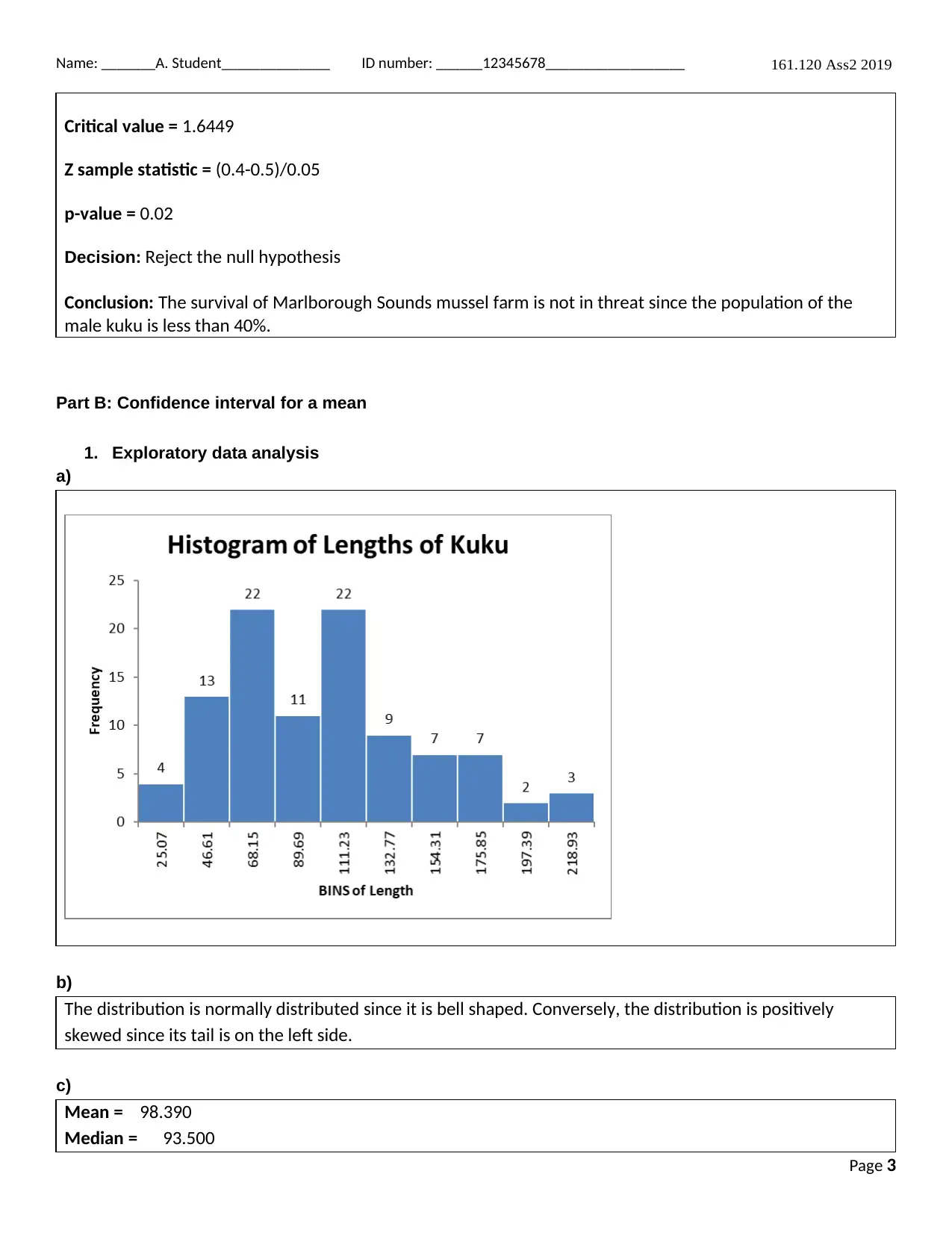
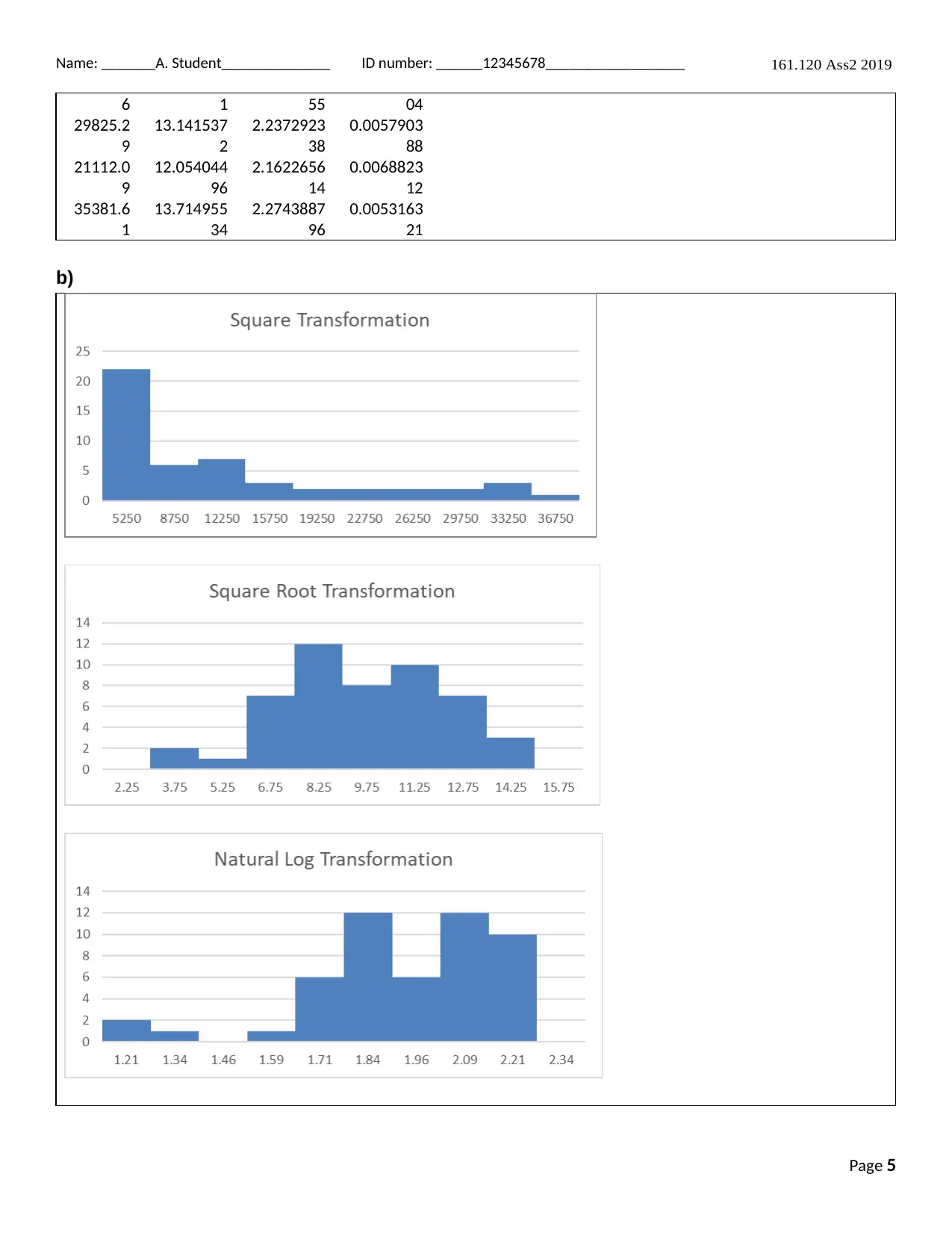
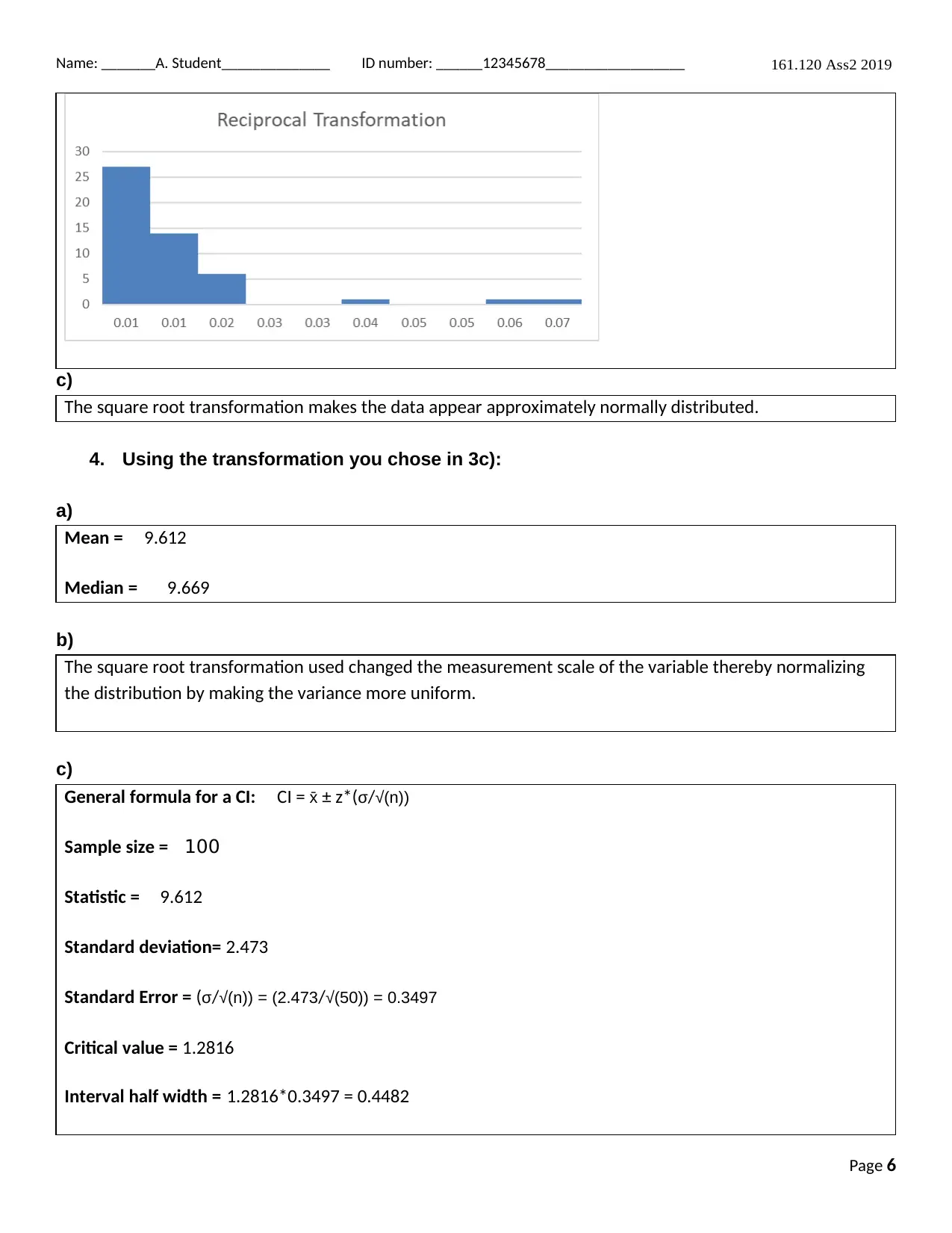
This document provides a confidence interval for the proportion and mean of kuku on Marlborough Sounds Mussel Farm. It includes exploratory data analysis, validity of the confidence interval, hypothesis, and interpretation. The document also discusses the transformation of data and its impact on the distribution.

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
161.120 Ass2 2019
Student’s name:
Student’s ID:
Page 1

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
Part A: Confidence Interval for a proportion [15 marks]
1. Proportion
The proportion of kuku that are female in the sample is 0.5
2. Confidence interval
General formula for a CI: CI = p̂ ± z * √ (p̂(1 - p̂)/n)
Sample size = 100
Statistic = 50
Standard Error = √(p̂(1 - p̂)/n) = √(0.5*(1-0.5)/100) = 0.05
Critical value = 1.6449
Interval half width = 1.6449 * 0.05 = 0.0822
95% CI = (0.5–0.0822, 0.5+0.822) = (0.4178, 0.5822)
Interpretation: We are 95% confident that the proportion of female kuku in the Marlborough Sounds
mussel farm is between 41.78% and 58.22%.
3. Validity of the confidence interval
The confidence interval is valid.
This conclusion is since there is a confidence level (95% confidence level), there is a statistic (50 or 0.5), and
that there is a margin of error (0.0822).
4. Conclusion
Hypothesis
H0: Proportion of male kuku is more than 40%
H1: Proportion of male kuku is less than or equal to 40%
General formula for a CI: z = (P - p̂)/SE
Sample size = 100
Statistic = 50
Standard Error = √ (p̂ (1 - p̂)/n) = √ (0.5*(1-0.5)/100) = 0.05
Page 2

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
Critical value = 1.6449
Z sample statistic = (0.4-0.5)/0.05
p-value = 0.02
Decision: Reject the null hypothesis
Conclusion: The survival of Marlborough Sounds mussel farm is not in threat since the population of the
male kuku is less than 40%.
Part B: Confidence interval for a mean
1. Exploratory data analysis
a)
b)
The distribution is normally distributed since it is bell shaped. Conversely, the distribution is positively
skewed since its tail is on the left side.
c)
Mean = 98.390
Median = 93.500
Page 3

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
Comment: It is evident that the distribution is positively skewed since the mean is grater than the
median.
2. Confidence interval
a)
General formula for a CI: CI = x̄ ± z*(σ/√(n))
Sample size = 50
Statistic = 98.39
Standard deviation = 46.66033
Standard Error = (σ/√(n)) = (46.66/√(50)) = 6.5988
Critical value = z = 1.2816
Interval half width = 8.4557
90% CI = (98.39-8.46, 98.39+8.46) = (89.93, 106.85)
Interpretation: We are 90% confident that the mean length of female kuku in the Marlborough Sounds
mussel farm is between 89.93 and 106.85.
b)
Since the distribution is skewed to the right based on the histogram, then there is a concern on the validity of the
confidence interval. This skewness violates the assumption of the central limit theorem which imply that the
independent values should be approximately normally distributed.
3. Transforming the data
a)
Square
Square
root
Natural
Log Reciprocal
28493.4
4
12.992305
42
2.2273724
42
0.0059241
71
31897.9 13.364131 2.2518814 0.0055991
Page 4

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
6 1 55 04
29825.2
9
13.141537
2
2.2372923
38
0.0057903
88
21112.0
9
12.054044
96
2.1622656
14
0.0068823
12
35381.6
1
13.714955
34
2.2743887
96
0.0053163
21
b)
Page 5

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
c)
The square root transformation makes the data appear approximately normally distributed.
4. Using the transformation you chose in 3c):
a)
Mean = 9.612
Median = 9.669
b)
The square root transformation used changed the measurement scale of the variable thereby normalizing
the distribution by making the variance more uniform.
c)
General formula for a CI: CI = x̄ ± z*(σ/√(n))
Sample size = 100
Statistic = 9.612
Standard deviation= 2.473
Standard Error = (σ/√(n)) = (2.473/√(50)) = 0.3497
Critical value = 1.2816
Interval half width = 1.2816*0.3497 = 0.4482
Page 6

161.120 Ass2 2019Name: _______A. Student______________ ID number: ______12345678__________________
90% CI = (9.612-0.4482, 9.612+0.4482) = (9.164, 10.060)
d)
Transformed median = 9.669
Back-transformed median = 9.669^2 = 93.49
CI formula: nq ± 1.96*√(nq(1-q))
Size: 50
q: 0.5
Critical Value: 1.2816
Standard error = √(nq(1-q)) = √(50*0.5(1-0.5)) = 3.536
Interval half width = 1.2816 * 3.536 = 4.53
90% CI: (93.49-4.53, 93.49+4.53) = (88.96, 98.02)
Interpretation: We are 90% confident that the median length of female kuku on the mussel farm is between
88.96 and 98.02.
Page 7