Building a Lift Operational Logic Circuit in Logisim

This assignment focuses on building a lift operational logic circuit in Logisim. It covers the inputs, restrictions, and successful operations of the lift.

Running head: COMPUTER SYSTEMS AND NETWORKS
COMPUTER SYSTEMS AND NETWORKS
Name of the Student
Name of the University
Author Note

1COMPUTER SYSTEMS AND NETWORKS
Introduction:
The main objective of this particular assignment is to build a lift operational logic circuit in
Logisim. The logic circuit has two inputs, namely C and D which has values in the range of 0
to 7 representing the floor numbers. Floor 0,4 and 6 are known to be private floors and the
operation of the lift from or to the private floors are restricted. Additionally, the lift does not
move when starting and destination floors are same. This is modelled by a Successful LED
light in the circuit. The LED is ON when lift movement is possible and the LED is OFF when
the lift movement is restricted. The input C and input D are modelled by C1,C2,C3 and
D1,D2 and D3 respectively with each having one bit.
Representation table of input C and D:
Successful operations from C to D:
1 to 2, 2 to 1, 1 to 3, 3 to 1, 1 to 5 , 5 to 1, 1 to 7, 7 to 1, 2 to 3, 3 to 2, 2 to 5, 5 to 2, 2 to 7, 7
to 2, 3 to 5, 5 to 3, 3 to 7, 7 to 3, 5 to 7, 7 to 5
Truth Table representation of C and D for Successful operation:
C1 C2 C3 D1 D2 D3 Successful

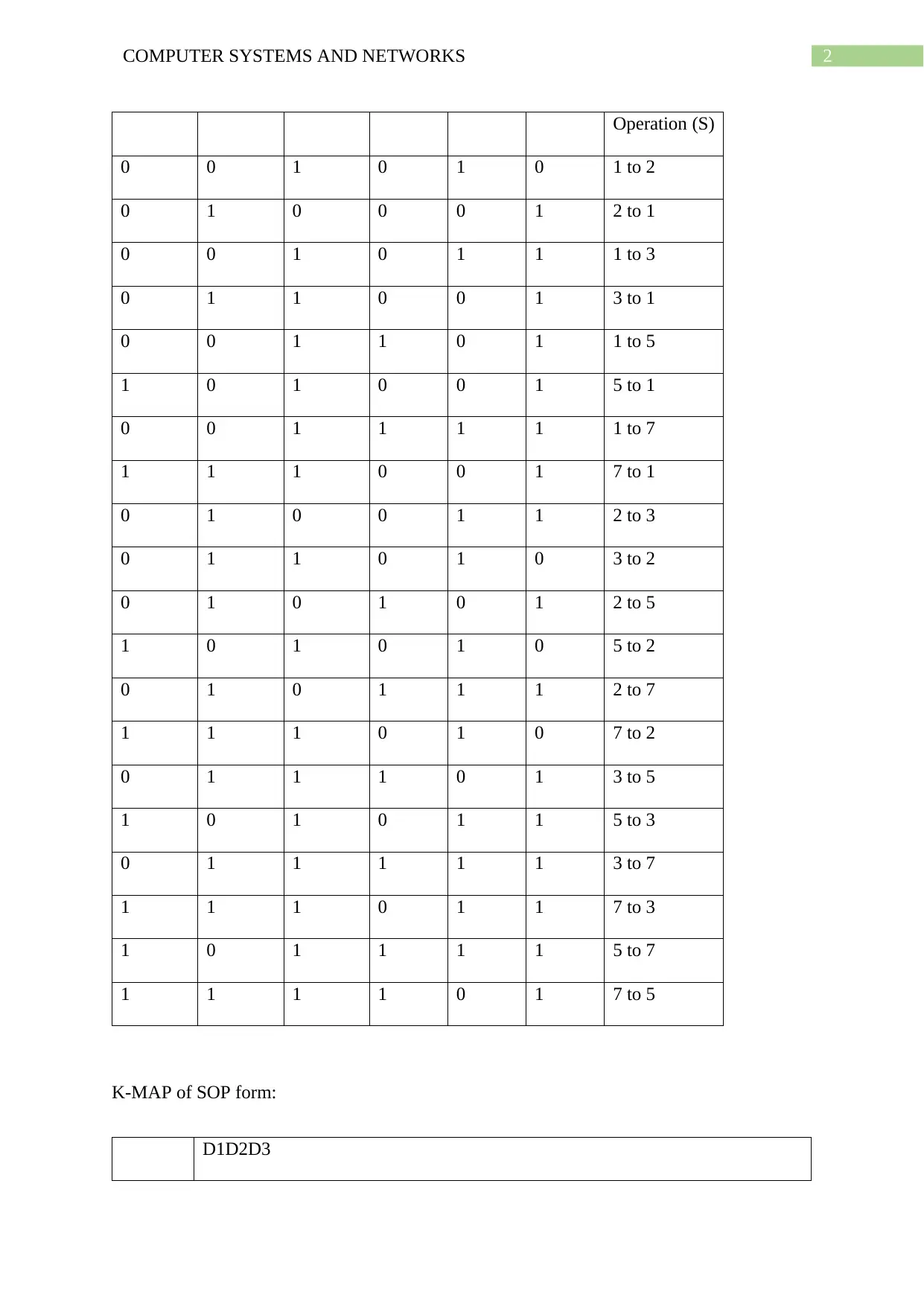
2COMPUTER SYSTEMS AND NETWORKS
Operation (S)
0 0 1 0 1 0 1 to 2
0 1 0 0 0 1 2 to 1
0 0 1 0 1 1 1 to 3
0 1 1 0 0 1 3 to 1
0 0 1 1 0 1 1 to 5
1 0 1 0 0 1 5 to 1
0 0 1 1 1 1 1 to 7
1 1 1 0 0 1 7 to 1
0 1 0 0 1 1 2 to 3
0 1 1 0 1 0 3 to 2
0 1 0 1 0 1 2 to 5
1 0 1 0 1 0 5 to 2
0 1 0 1 1 1 2 to 7
1 1 1 0 1 0 7 to 2
0 1 1 1 0 1 3 to 5
1 0 1 0 1 1 5 to 3
0 1 1 1 1 1 3 to 7
1 1 1 0 1 1 7 to 3
1 0 1 1 1 1 5 to 7
1 1 1 1 0 1 7 to 5
K-MAP of SOP form:
D1D2D3

3COMPUTER SYSTEMS AND NETWORKS
C1C2C3 000 001 011 010 110 111 101 100
000 0 0 0 0 0 0 0 0
001 0 0 1 1 0 1 1 0
011 0 1 0 1 0 1 1 0
010 0 1 1 0 0 1 1 0
110 0 0 0 0 0 0 0 0
111 0 1 1 1 0 0 1 0
101 0 1 1 1 0 1 0 0
100 0 0 0 0 0 0 0 0
S = ∑
m
(10,11,13,15,17,19,21,23,25,26,29,31,41,42,43,47,57,58,59,61)
Solution of the K-map gives minimum SOP expression as given below.
Minimized Boolean Expression:
S = C1'C2C3'D3 + C3D1'D2D3' + C2'C3D1'D2 + C1C3D1'D3 + C2C3D2'D3 + C1'C3D1D3
+ C2'C3D2D3
Logisim Circuit Diagram:

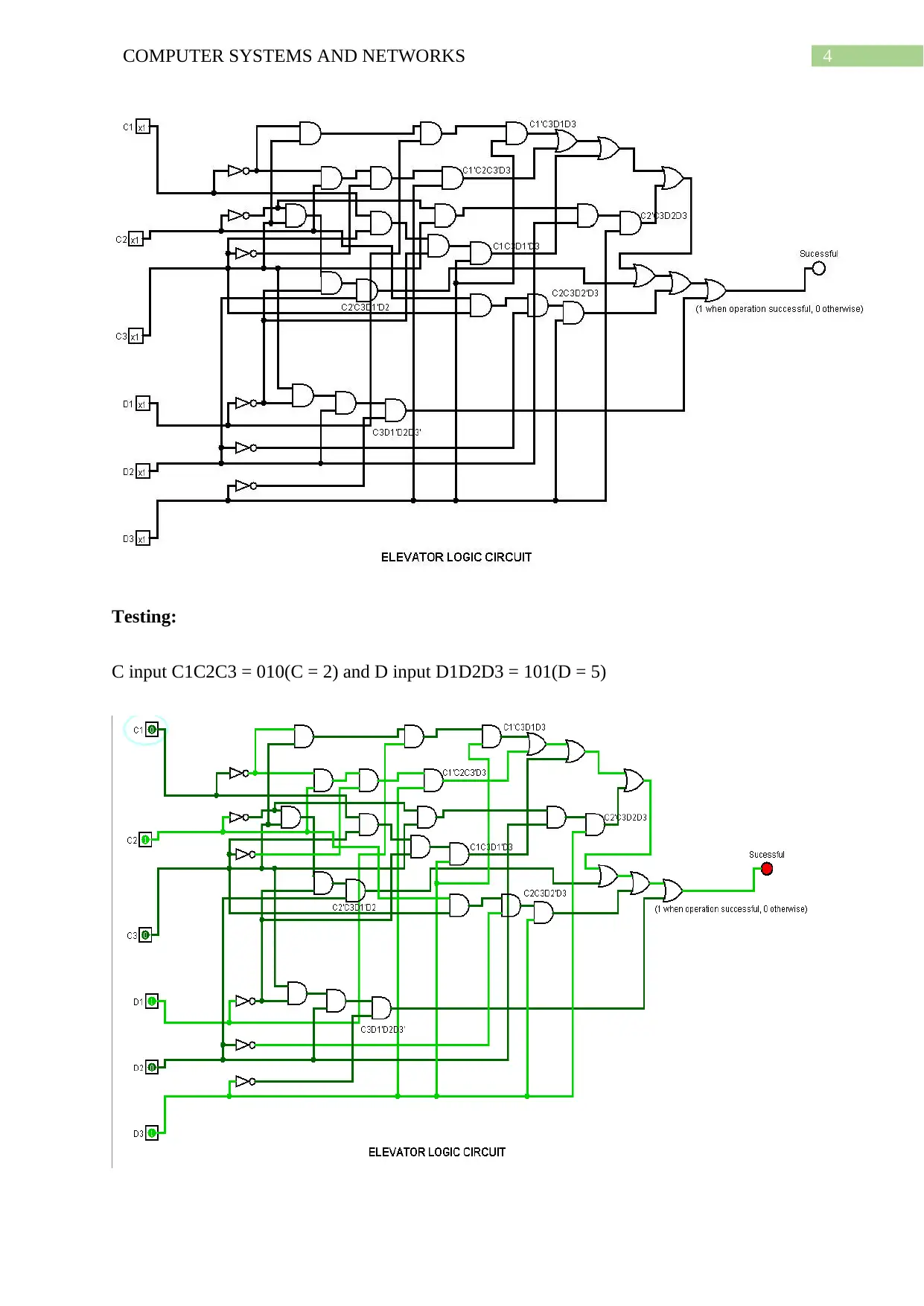
4COMPUTER SYSTEMS AND NETWORKS
Testing:
C input C1C2C3 = 010(C = 2) and D input D1D2D3 = 101(D = 5)

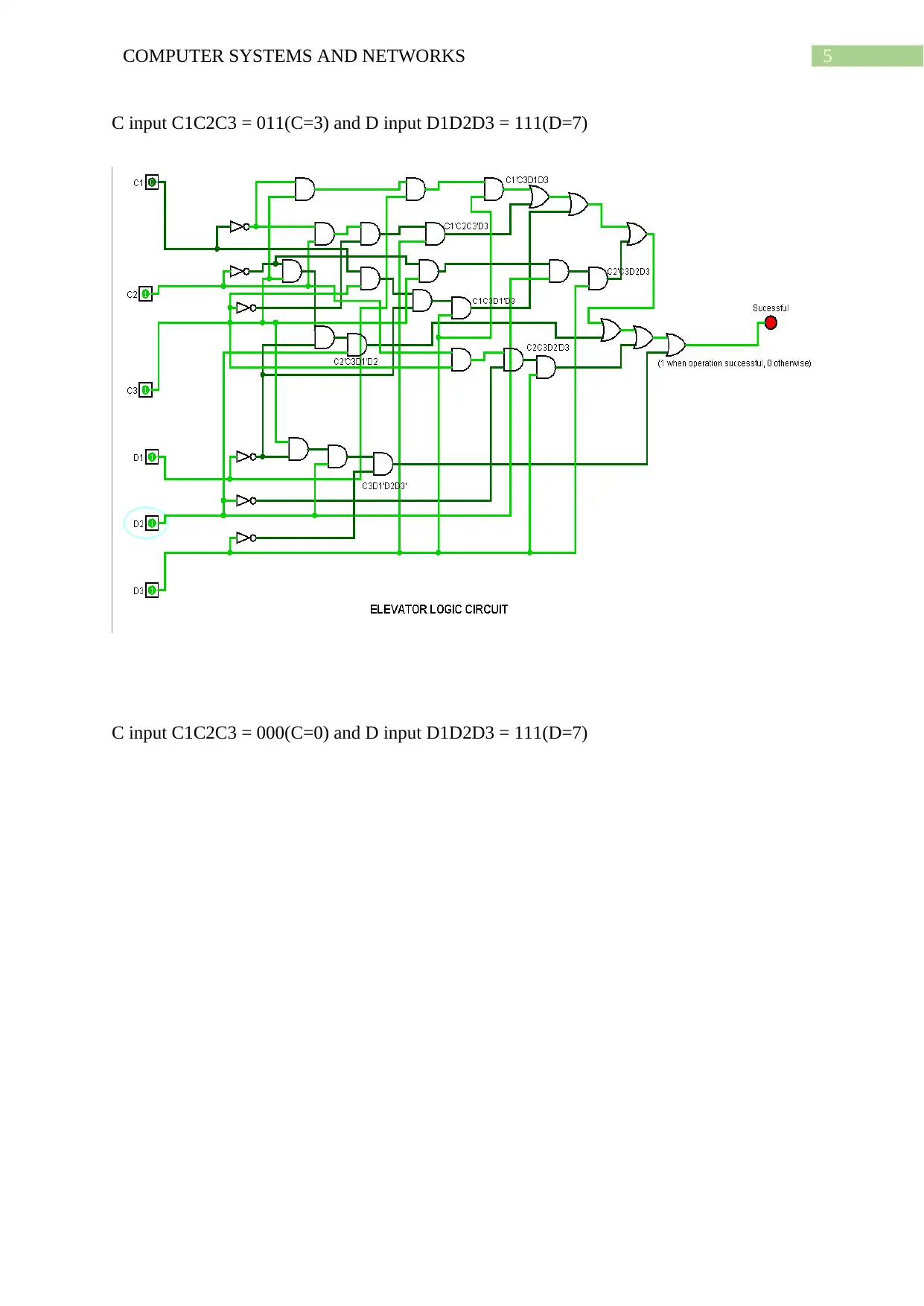
5COMPUTER SYSTEMS AND NETWORKS
C input C1C2C3 = 011(C=3) and D input D1D2D3 = 111(D=7)
C input C1C2C3 = 000(C=0) and D input D1D2D3 = 111(D=7)

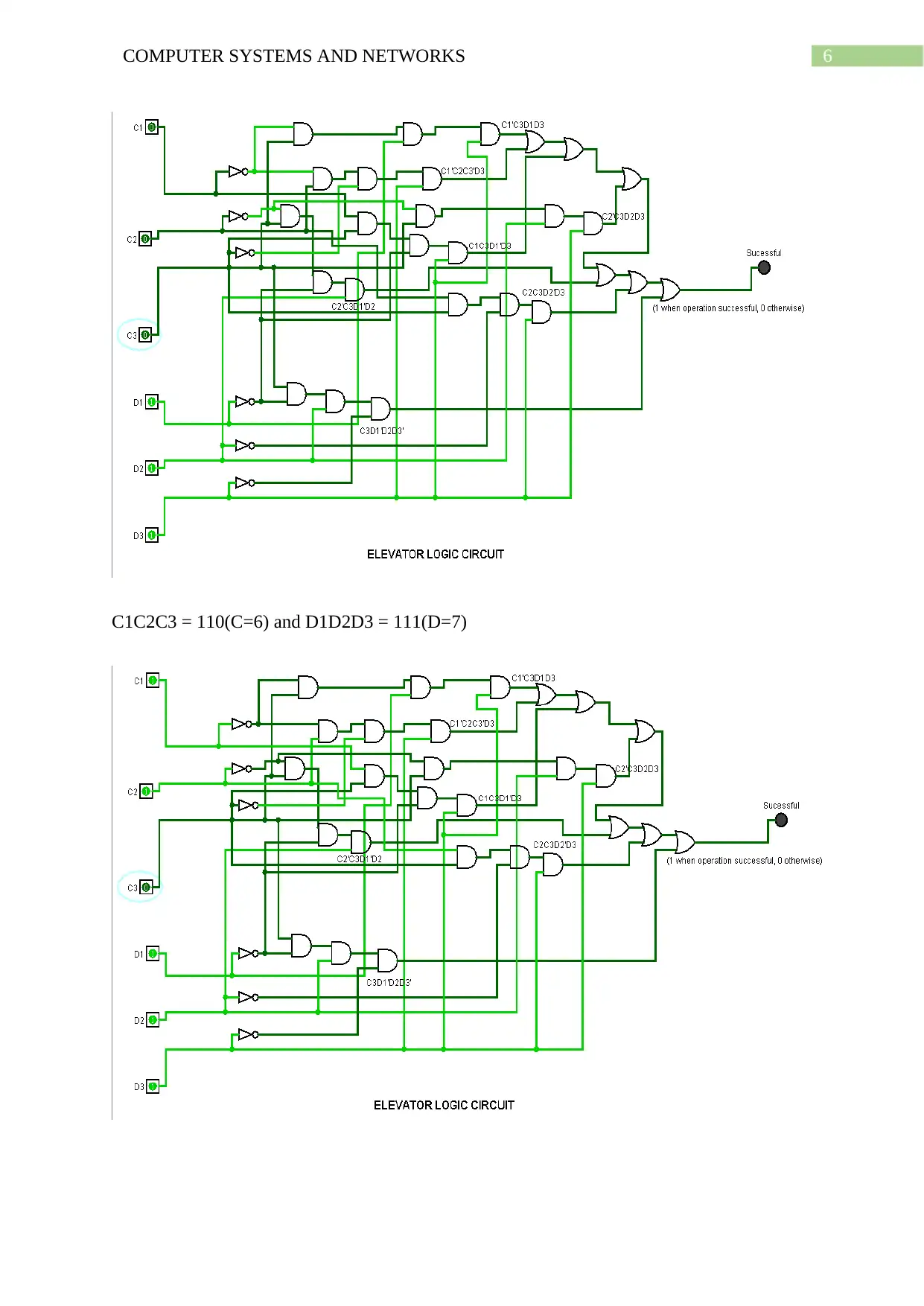
6COMPUTER SYSTEMS AND NETWORKS
C1C2C3 = 110(C=6) and D1D2D3 = 111(D=7)

7COMPUTER SYSTEMS AND NETWORKS
It is evident from the testing that the lift movement is working according to the truth table.
The first test is Successful as C=2 and D= 5 and both are valid input for movement. The
second test is also Successful as C=3 and D=7 and both operations are valid. However, in the
third test is not Successful as C=0 (a private floor) and D = 7 (valid for movement). This way
as the destination floor is private in fourth test (as C =110 and D=111) the lift movement is
Unsuccessful.
Conclusion:
Thus in conclusion it can be stated that design of the lift movement logic circuit is
successfully implemented as all the operations of the lift is according to the truth table for
Successful operation. This Successful operation is realized from the ON state of Successful
LED in the logic circuit. The method sum of product and then K-MAP technique is used here
to build the logic circuit. A slightly different approach of providing only permitted states of C
and D through two 3 to 8 decoders can be used to make the same operation of circuit,
however in that case the number of primary gates will be larger and thus the circuit is in-
efficient from the point of view of cost of the circuit. The circuit can further be integrated to
count the number of successful and unsuccessful operation and locking the circuit operation
after a certain number of Unsuccessful operations. This can be realized by mainly a counter
and other necessary gates, but due to complexity and size of circuit this advance design is not
implemented here. Thus the design of the circuit is appropriate based on the stated specific
operations of the lift.