SEO Title: Desklib - Online Library for Study Material with Solved Assignments

The article includes solved assignments on statistics, probability, and market segmentation. It also covers measures of central tendency, correlation, and regression analysis. The content is relevant to various courses and universities.

Running head: STATISTICS ASSIGNMENT
STATISTICS ASSIGNMENT
Name of student
Name of University

1STATISTICS ASSIGNMENT
Table of Contents
Question 1........................................................................................................................................2
Question 2........................................................................................................................................3
Question 3........................................................................................................................................5
Question 4........................................................................................................................................6
Question 5........................................................................................................................................8
Question 6........................................................................................................................................9
Question 7......................................................................................................................................10
Question 8......................................................................................................................................10

2STATISTICS ASSIGNMENT
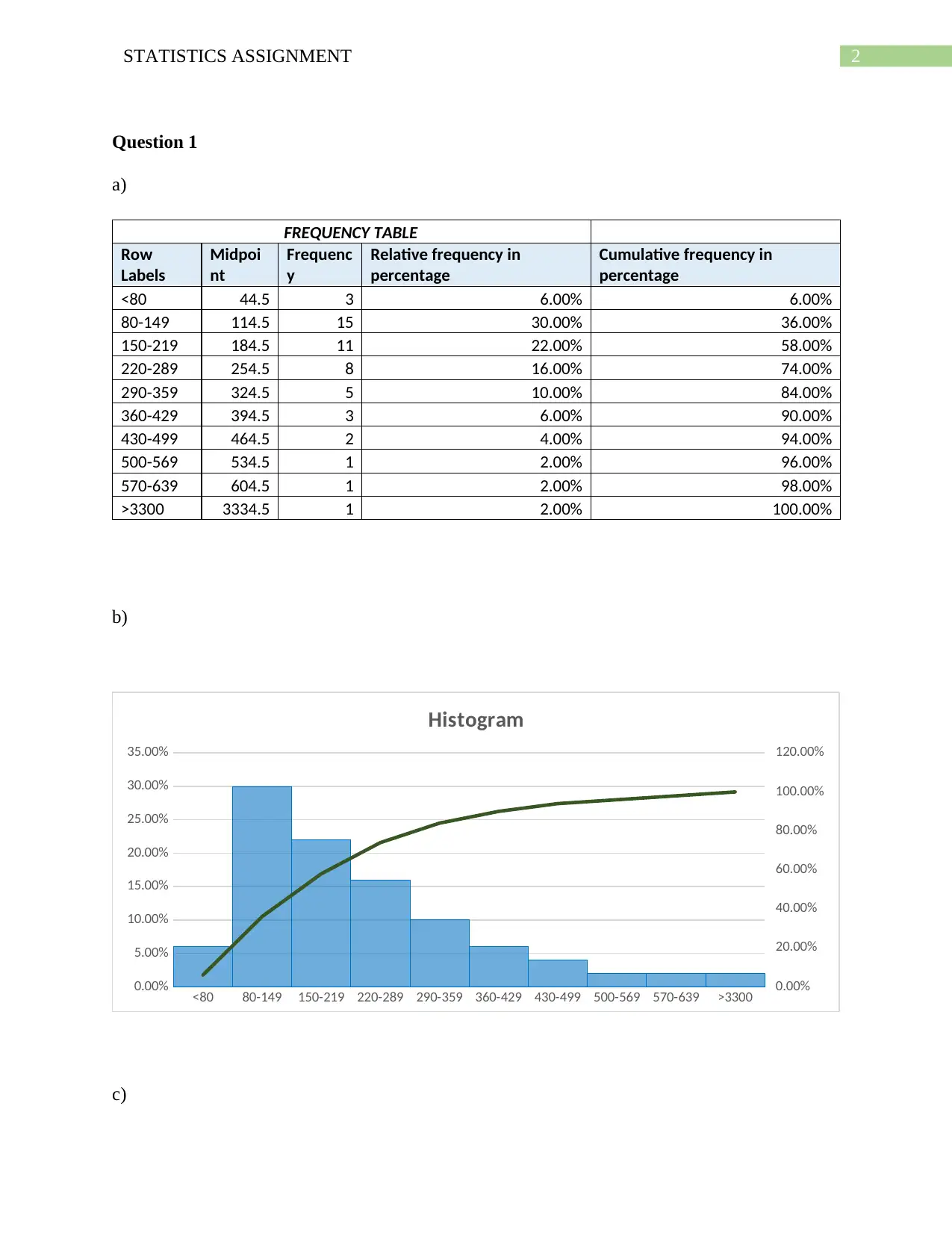
Question 1
a)
FREQUENCY TABLE
Row
Labels
Midpoi
nt
Frequenc
y
Relative frequency in
percentage
Cumulative frequency in
percentage
<80 44.5 3 6.00% 6.00%
80-149 114.5 15 30.00% 36.00%
150-219 184.5 11 22.00% 58.00%
220-289 254.5 8 16.00% 74.00%
290-359 324.5 5 10.00% 84.00%
360-429 394.5 3 6.00% 90.00%
430-499 464.5 2 4.00% 94.00%
500-569 534.5 1 2.00% 96.00%
570-639 604.5 1 2.00% 98.00%
>3300 3334.5 1 2.00% 100.00%
b)
<80 80-149 150-219 220-289 290-359 360-429 430-499 500-569 570-639 >3300
0.00%
5.00%
10.00%
15.00%
20.00%
25.00%
30.00%
35.00%
0.00%
20.00%
40.00%
60.00%
80.00%
100.00%
120.00%
Histogram
c)

3STATISTICS ASSIGNMENT
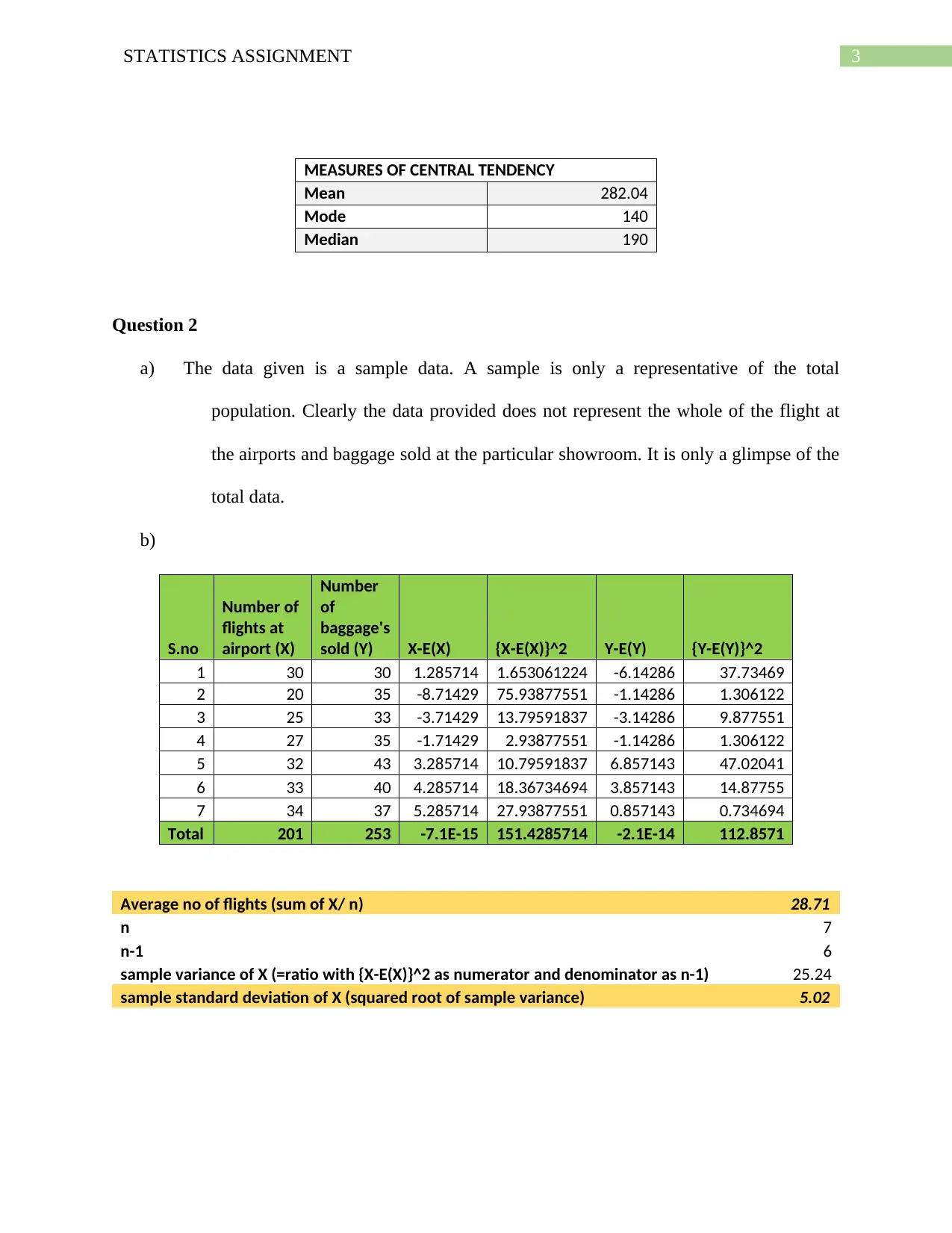
MEASURES OF CENTRAL TENDENCY
Mean 282.04
Mode 140
Median 190
Question 2
a) The data given is a sample data. A sample is only a representative of the total
population. Clearly the data provided does not represent the whole of the flight at
the airports and baggage sold at the particular showroom. It is only a glimpse of the
total data.
b)
S.no
Number of
flights at
airport (X)
Number
of
baggage's
sold (Y) X-E(X) {X-E(X)}^2 Y-E(Y) {Y-E(Y)}^2
1 30 30 1.285714 1.653061224 -6.14286 37.73469
2 20 35 -8.71429 75.93877551 -1.14286 1.306122
3 25 33 -3.71429 13.79591837 -3.14286 9.877551
4 27 35 -1.71429 2.93877551 -1.14286 1.306122
5 32 43 3.285714 10.79591837 6.857143 47.02041
6 33 40 4.285714 18.36734694 3.857143 14.87755
7 34 37 5.285714 27.93877551 0.857143 0.734694
Total 201 253 -7.1E-15 151.4285714 -2.1E-14 112.8571
Average no of flights (sum of X/ n) 28.71
n 7
n-1 6
sample variance of X (=ratio with {X-E(X)}^2 as numerator and denominator as n-1) 25.24
sample standard deviation of X (squared root of sample variance) 5.02

4STATISTICS ASSIGNMENT
c)
sample standard deviation of Y 4.34
3rd quartile of Y (Q3) 38.50
1st quartile of Y (Q1) 34.00
IQR of Y (= Q3-Q1) 4.50
The inter quartile range is preferred over the standard deviation when the data has
outliers or extreme values. This is because the IQR is not affected by the presence of outliers
unlike the mean and hence the standard deviation. Suppose in the current data, a value of number
of baggage for a particular day was uncharacteristically high, taking value 100. This would mean
that the mean would also be inflated and hence the standard deviation. However this is
misleading as this is a rare event. The IQR however would not change as the quartile values
would not change much due to its dependence on the ordering of the data and will be immune to
the bias arising out of the outlier. The calculations and discrepancy in given as follows:
standard deviation of Y with outlier
22.9311
9
3rd quartile of Y with outlier 40.75
1st quartile of Y with outlier 34.50
IQR of Y with outlier 6.25
d)
Correlation (X,Y) = 0.45
This means that the Y increase with X and vice versa. The correlation is positive and
moderate. Thus being a manager, I would stalk up more bags and put them on display on the day
that more flights are scheduled.

5STATISTICS ASSIGNMENT
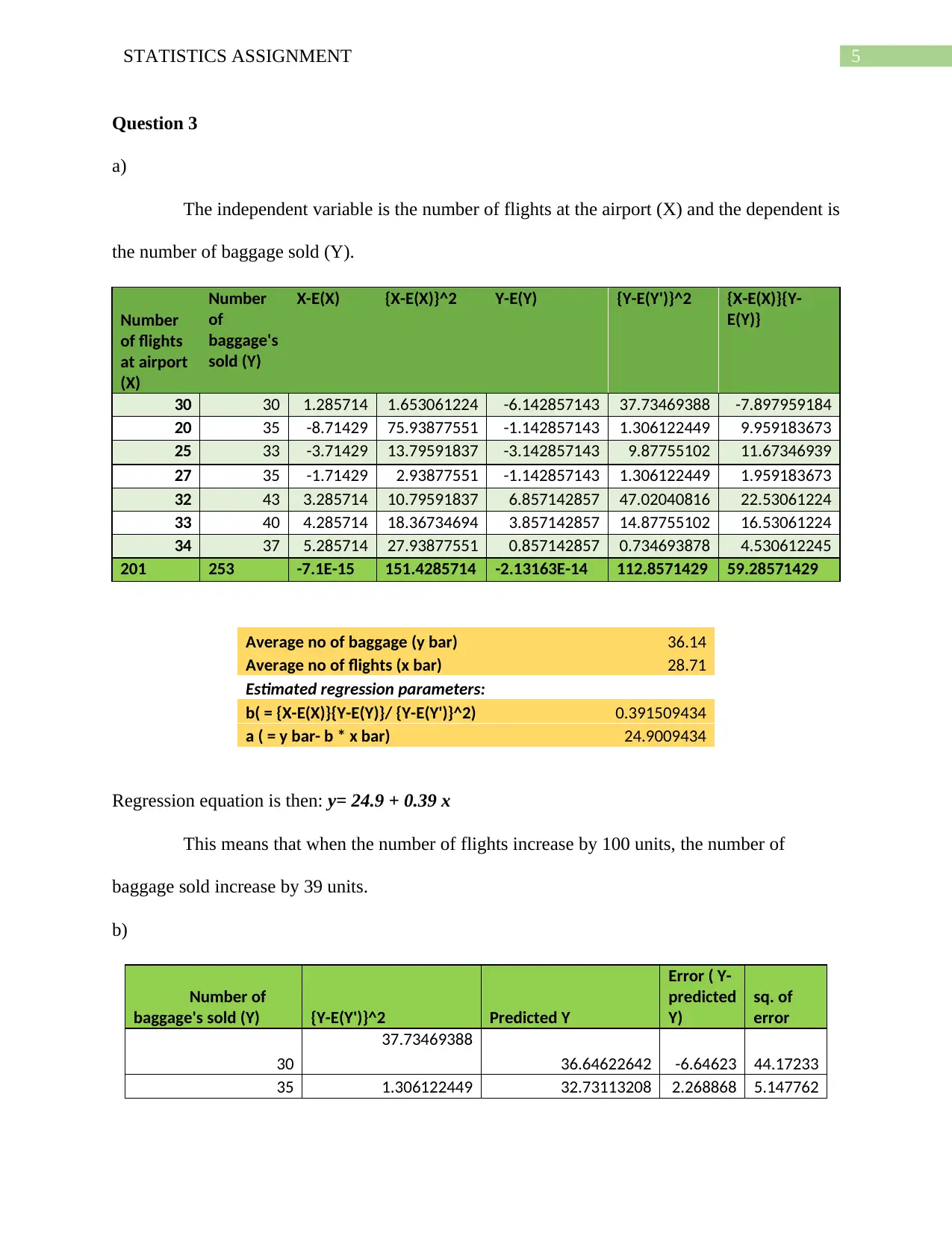
Question 3
a)
The independent variable is the number of flights at the airport (X) and the dependent is
the number of baggage sold (Y).
Number
of flights
at airport
(X)
Number
of
baggage's
sold (Y)
X-E(X) {X-E(X)}^2 Y-E(Y) {Y-E(Y')}^2 {X-E(X)}{Y-
E(Y)}
30 30 1.285714 1.653061224 -6.142857143 37.73469388 -7.897959184
20 35 -8.71429 75.93877551 -1.142857143 1.306122449 9.959183673
25 33 -3.71429 13.79591837 -3.142857143 9.87755102 11.67346939
27 35 -1.71429 2.93877551 -1.142857143 1.306122449 1.959183673
32 43 3.285714 10.79591837 6.857142857 47.02040816 22.53061224
33 40 4.285714 18.36734694 3.857142857 14.87755102 16.53061224
34 37 5.285714 27.93877551 0.857142857 0.734693878 4.530612245
201 253 -7.1E-15 151.4285714 -2.13163E-14 112.8571429 59.28571429
Average no of baggage (y bar) 36.14
Average no of flights (x bar) 28.71
Estimated regression parameters:
b( = {X-E(X)}{Y-E(Y)}/ {Y-E(Y')}^2) 0.391509434
a ( = y bar- b * x bar) 24.9009434
Regression equation is then: y= 24.9 + 0.39 x
This means that when the number of flights increase by 100 units, the number of
baggage sold increase by 39 units.
b)
Number of
baggage's sold (Y) {Y-E(Y')}^2 Predicted Y
Error ( Y-
predicted
Y)
sq. of
error
30
37.73469388
36.64622642 -6.64623 44.17233
35 1.306122449 32.73113208 2.268868 5.147762

6STATISTICS ASSIGNMENT
33
9.87755102
34.68867925 -1.68868 2.851638
35
1.306122449
35.47169811 -0.4717 0.222499
43
47.02040816
37.42924528 5.570755 31.03331
40
14.87755102
37.82075472 2.179245 4.74911
37
0.734693878
38.21226415 -1.21226 1.469584
253
112.8571429
253 -1.4E-14 89.64623
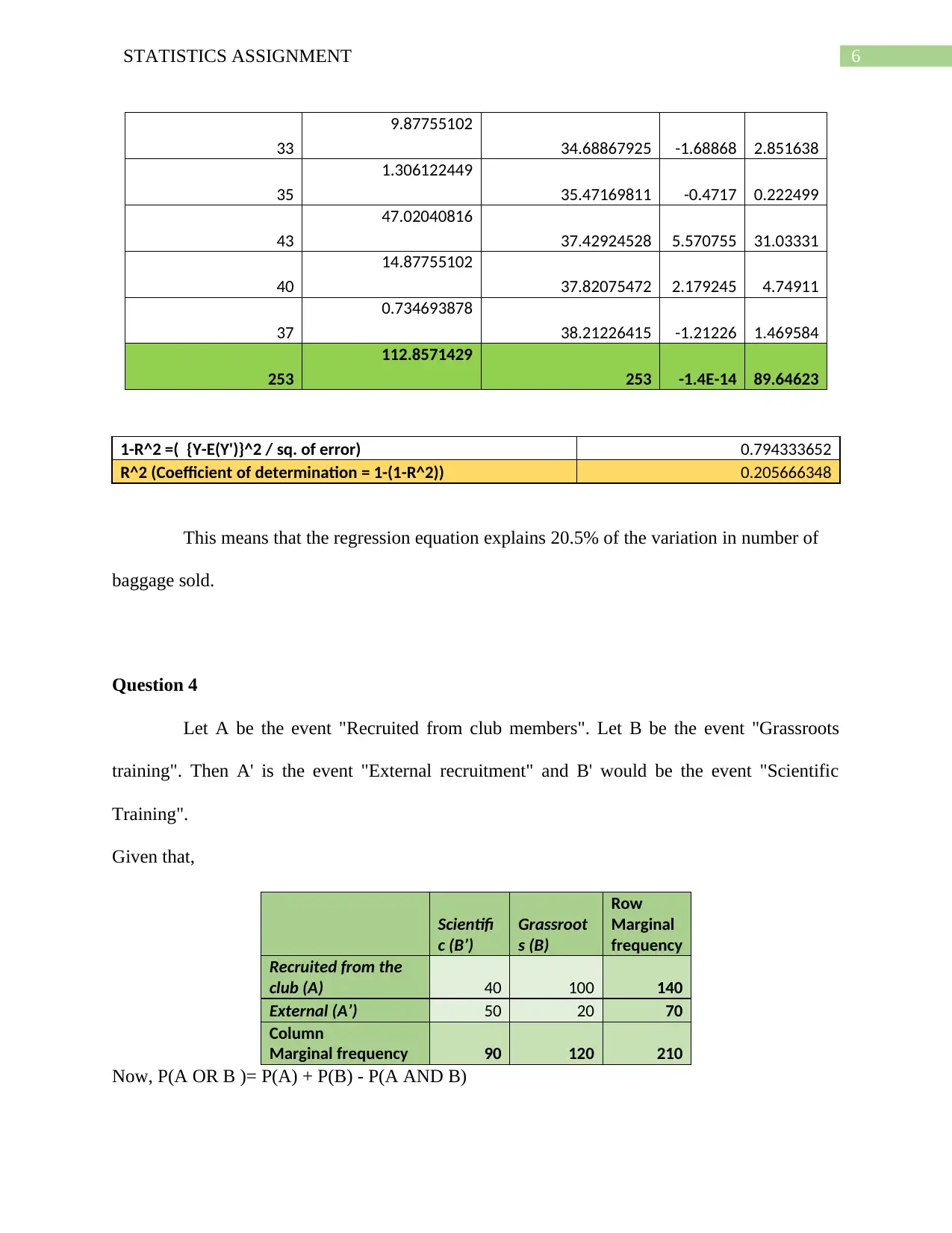
1-R^2 =( {Y-E(Y')}^2 / sq. of error) 0.794333652
R^2 (Coefficient of determination = 1-(1-R^2)) 0.205666348
This means that the regression equation explains 20.5% of the variation in number of
baggage sold.
Question 4
Let A be the event "Recruited from club members". Let B be the event "Grassroots
training". Then A' is the event "External recruitment" and B' would be the event "Scientific
Training".
Given that,
Scientifi
c (B’)
Grassroot
s (B)
Row
Marginal
frequency
Recruited from the
club (A) 40 100 140
External (A’) 50 20 70
Column
Marginal frequency 90 120 210
Now, P(A OR B )= P(A) + P(B) - P(A AND B)

7STATISTICS ASSIGNMENT
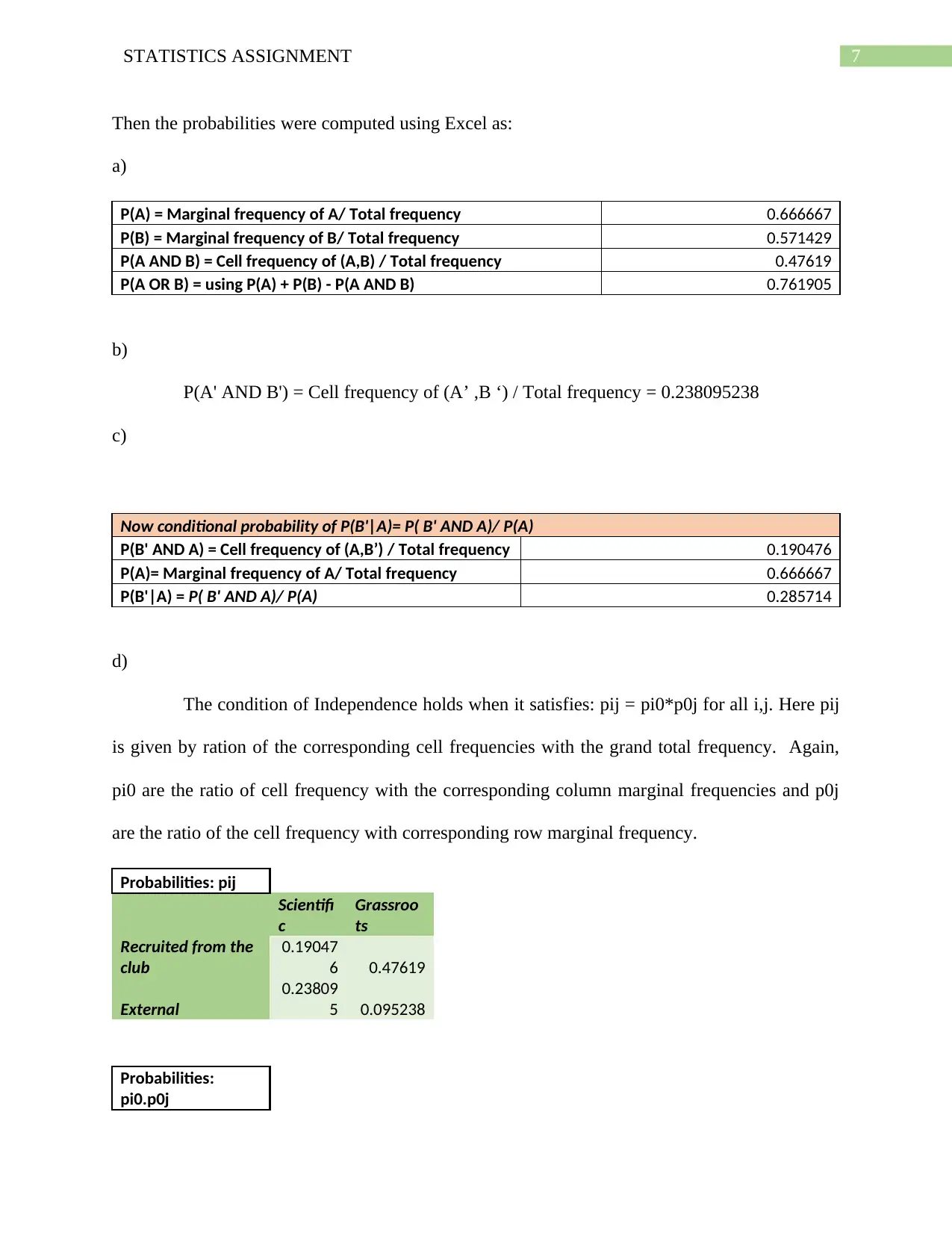
Then the probabilities were computed using Excel as:
a)
P(A) = Marginal frequency of A/ Total frequency 0.666667
P(B) = Marginal frequency of B/ Total frequency 0.571429
P(A AND B) = Cell frequency of (A,B) / Total frequency 0.47619
P(A OR B) = using P(A) + P(B) - P(A AND B) 0.761905
b)
P(A' AND B') = Cell frequency of (A’ ,B ‘) / Total frequency = 0.238095238
c)
Now conditional probability of P(B'|A)= P( B' AND A)/ P(A)
P(B' AND A) = Cell frequency of (A,B’) / Total frequency 0.190476
P(A)= Marginal frequency of A/ Total frequency 0.666667
P(B'|A) = P( B' AND A)/ P(A) 0.285714
d)
The condition of Independence holds when it satisfies: pij = pi0*p0j for all i,j. Here pij
is given by ration of the corresponding cell frequencies with the grand total frequency. Again,
pi0 are the ratio of cell frequency with the corresponding column marginal frequencies and p0j
are the ratio of the cell frequency with corresponding row marginal frequency.
Probabilities: pij
Scientifi
c
Grassroo
ts
Recruited from the
club
0.19047
6 0.47619
External
0.23809
5 0.095238
Probabilities:
pi0.p0j

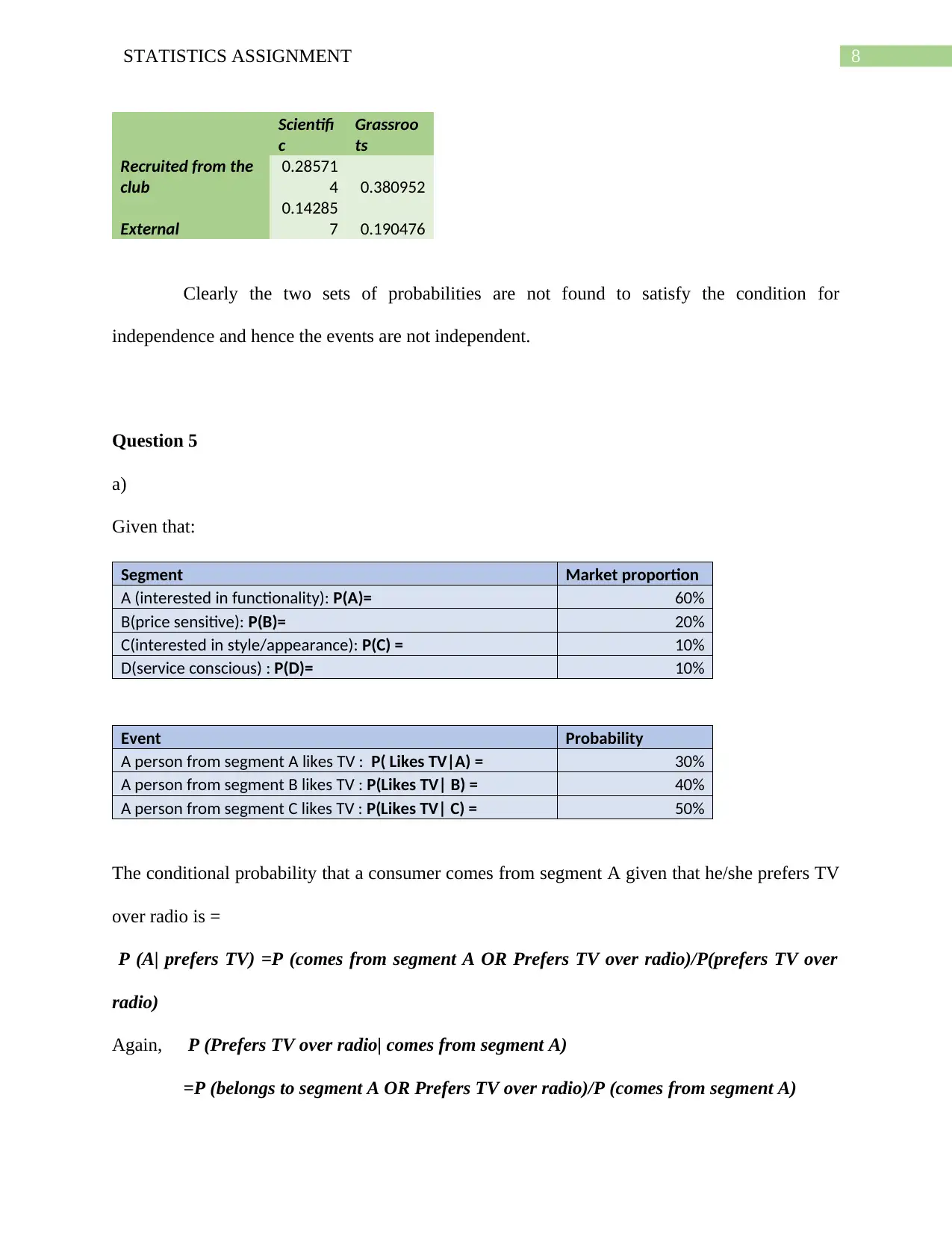
8STATISTICS ASSIGNMENT
Scientifi
c
Grassroo
ts
Recruited from the
club
0.28571
4 0.380952
External
0.14285
7 0.190476
Clearly the two sets of probabilities are not found to satisfy the condition for
independence and hence the events are not independent.
Question 5
a)
Given that:
Segment Market proportion
A (interested in functionality): P(A)= 60%
B(price sensitive): P(B)= 20%
C(interested in style/appearance): P(C) = 10%
D(service conscious) : P(D)= 10%
Event Probability
A person from segment A likes TV : P( Likes TV|A) = 30%
A person from segment B likes TV : P(Likes TV| B) = 40%
A person from segment C likes TV : P(Likes TV| C) = 50%
The conditional probability that a consumer comes from segment A given that he/she prefers TV
over radio is =
P (A| prefers TV) =P (comes from segment A OR Prefers TV over radio)/P(prefers TV over
radio)
Again, P (Prefers TV over radio| comes from segment A)
=P (belongs to segment A OR Prefers TV over radio)/P (comes from segment A)

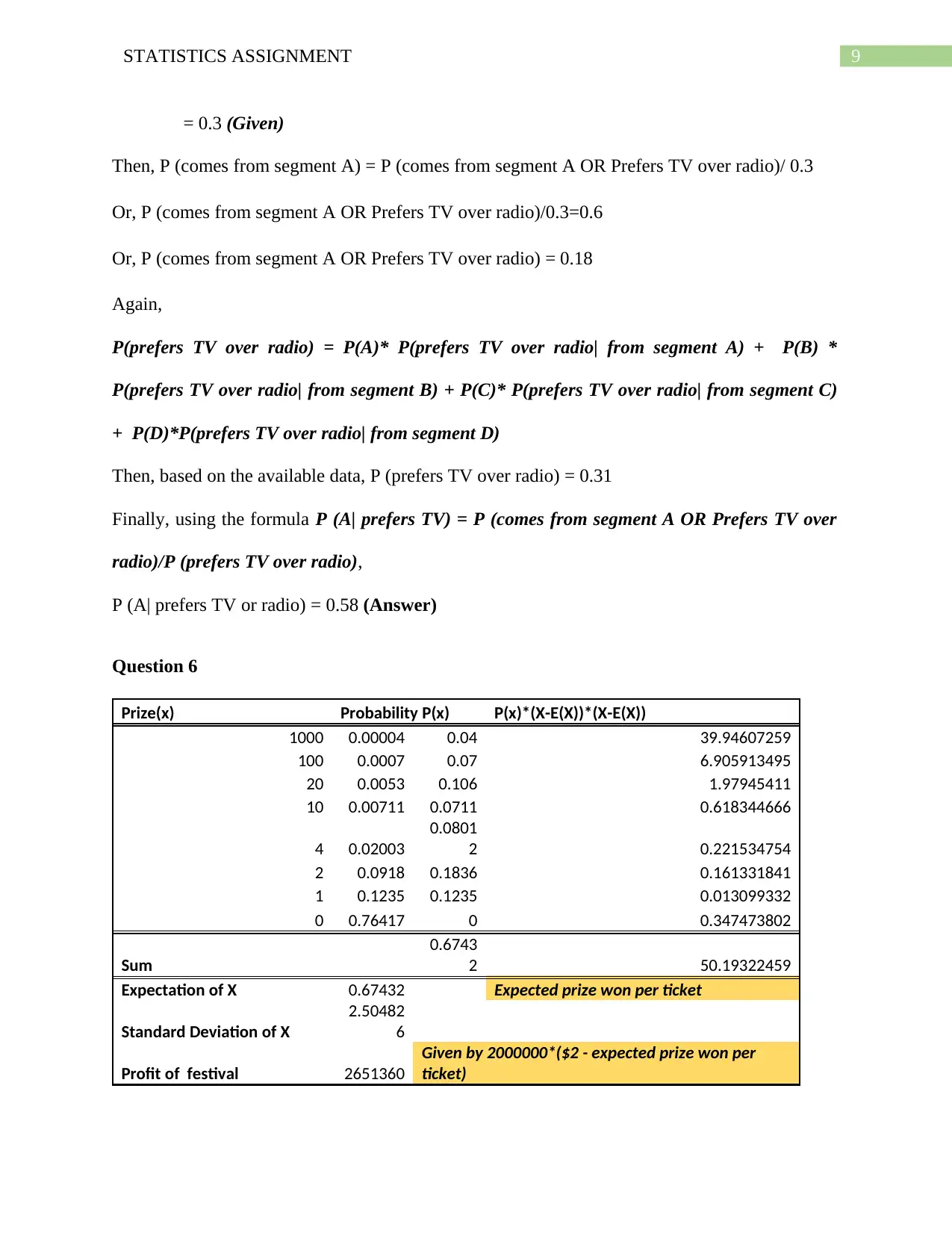
9STATISTICS ASSIGNMENT
= 0.3 (Given)
Then, P (comes from segment A) = P (comes from segment A OR Prefers TV over radio)/ 0.3
Or, P (comes from segment A OR Prefers TV over radio)/0.3=0.6
Or, P (comes from segment A OR Prefers TV over radio) = 0.18
Again,
P(prefers TV over radio) = P(A)* P(prefers TV over radio| from segment A) + P(B) *
P(prefers TV over radio| from segment B) + P(C)* P(prefers TV over radio| from segment C)
+ P(D)*P(prefers TV over radio| from segment D)
Then, based on the available data, P (prefers TV over radio) = 0.31
Finally, using the formula P (A| prefers TV) = P (comes from segment A OR Prefers TV over
radio)/P (prefers TV over radio),
P (A| prefers TV or radio) = 0.58 (Answer)
Question 6
Prize(x) Probability P(x) P(x)*(X-E(X))*(X-E(X))
1000 0.00004 0.04 39.94607259
100 0.0007 0.07 6.905913495
20 0.0053 0.106 1.97945411
10 0.00711 0.0711 0.618344666
4 0.02003
0.0801
2 0.221534754
2 0.0918 0.1836 0.161331841
1 0.1235 0.1235 0.013099332
0 0.76417 0 0.347473802
Sum
0.6743
2 50.19322459
Expectation of X 0.67432 Expected prize won per ticket
Standard Deviation of X
2.50482
6
Profit of festival 2651360
Given by 2000000*($2 - expected prize won per
ticket)

10STATISTICS ASSIGNMENT
Question 7
Given that,
mean speed of train travelling from Kyoto to Tokyo is = 250
standard deviation of speed of train travelling from Kyoto to Tokyo is = 30
Assume that the speed of the train follows a normal distribution and is denoted by X. Then X
follows Normal(250,30)
a)
P(X< 200)= 0.04779 (Answer)
b)
P(X>300)= 0.04779 (Answer)
c)
P(210<X<280) = P( X<280) - P(X<210)
P(X<280)= 0.841345
P(X<210)= 0.091211
P(210<X<280) = 0.750134 (Answer)
Question 8
Let X denote the average number of shoppers visiting a center during a 1 hour period
The Assuming that X follows Normal distribution
Given than mean of X is 448
and that the standard deviation of X is 21
Then the statistic , mean of X, denoted by say Xbar computed from a random sample of
size 49 (= 7*7), follows Normal(448, 21/7)
P( 441 < Xbar < 446) = P( Xbar < 446) - P( Xbar < 441)
P( Xbar < 441)
0.009815
329
P( Xbar < 446) 0.252492

11STATISTICS ASSIGNMENT
538
P( 441 < Xbar < 446) =
0.242677
209 (Answer)