Electrical and Electronic Engineering Problems

This document provides solutions to various electrical and electronic engineering problems. It covers topics such as calculating currents, voltages, and resistances using Kirchhoff's Laws and Ohm's Law. The problems involve series and parallel resistors, circuit simplification using Norton's and Thevenin's theorems, and analyzing complex waveforms.

ELECTRICAL AND ELECTRONIC ENGINEERING PROBLEMS
By Name
Course
Instructor
Institution
Location
Date

Task 1 a
a. Using the laws of Series and Parallel resistors calculate the total current (It) flowing in the
network below.
b. Then use Kirchoff’s Laws to calculate the current flowing in each of the branches containing
the resistors numbered R1 to R5.
a) At C
1
RC
= 1
R1
+ 1
R2
1
RC
= 1
2.4 + 1
1.7 =1.0049
Rc=0.995 Ω
At F
1
RF
= 1
R3
+ 1
R4
+ 1
R5
1
RF
= 1
60 + 1
20 + 1
30 =0.1 Ω
RF=10 Ω
Hence, total resistance, RT =10 Ω+0.995 Ω
RT =10.995 Ω
From Ohms Law, I = V/R
I T= V
RT
= 132
10.995 =12.005 A
b) Kirchhoff’s Current Law Equivalent Circuit

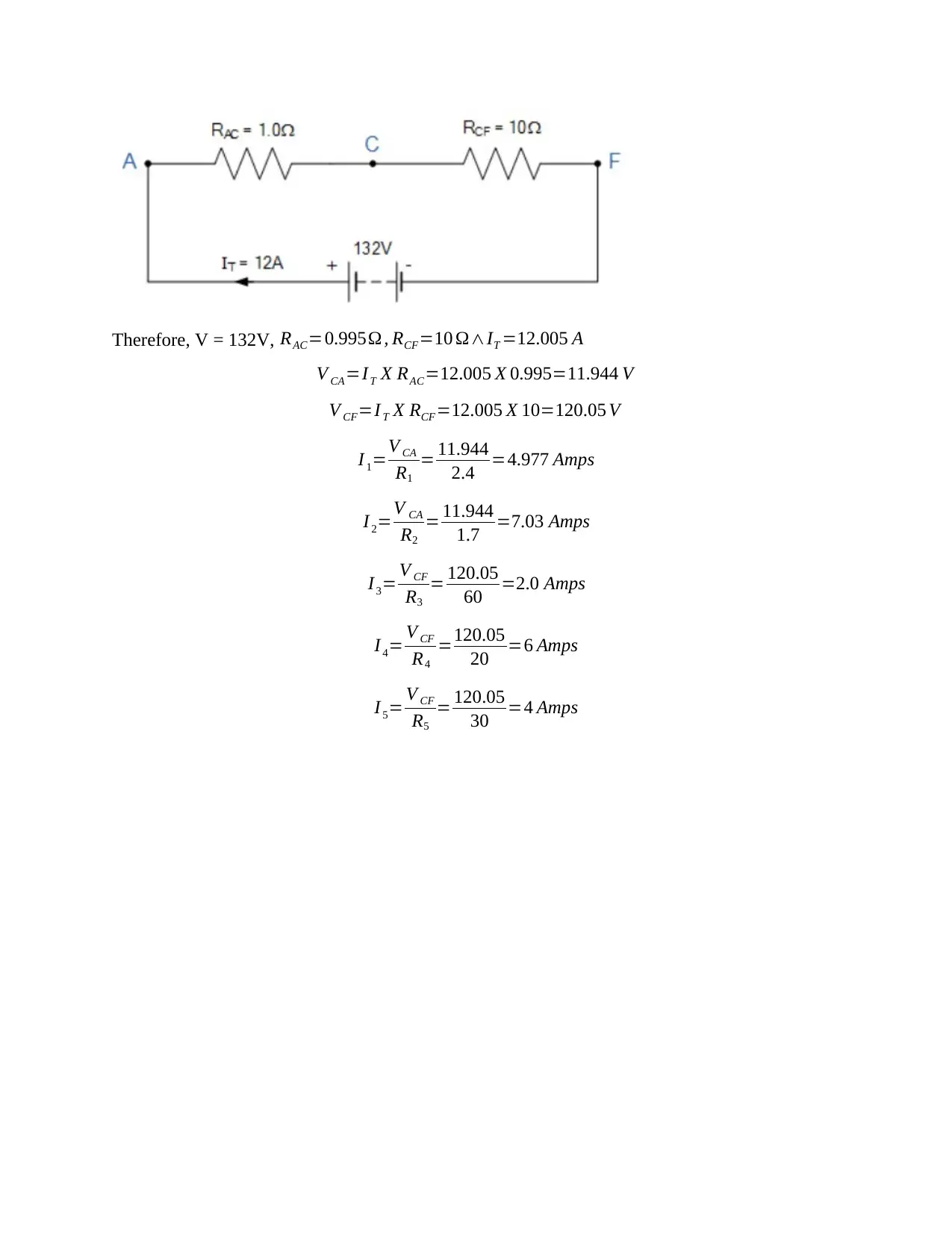
Therefore, V = 132V, RAC=0.995Ω , RCF=10 Ω∧IT =12.005 A
V CA=I T X RAC=12.005 X 0.995=11.944 V
V CF=I T X RCF=12.005 X 10=120.05 V
I 1=V CA
R1
= 11.944
2.4 =4.977 Amps
I 2=V CA
R2
= 11.944
1.7 =7.03 Amps
I3= V CF
R3
= 120.05
60 =2.0 Amps
I 4= V CF
R4
=120.05
20 =6 Amps
I 5= V CF
R5
= 120.05
30 =4 Amps

Task 1b
Using Kirchoff’s Laws for currents and voltages in networks, calculate the currents flowing in
R1, R2 and R3.
Using Kirchhoffs Current Law, KCL the equations are given as:
At node B: I 3=I 1 +I2 ……………………… (i)
At node A: I 1+ I 2=I 3
Using Kirchhoffs Voltage Law, KVL the equations are given as:
Loop 1:
10=R1 I 1+ R3 I3=10 I1+ 40 I 3
Loop 2:
20=R2 I2 + R3 I3=20 I 2+ 40 I3
Loop 3:
20−10=10 I 1−20 I 2
From equation (i)
10=50 I 1 +40 I 2=10 I 1 +40 ( I 1 +I2 )
And
20=20 I2 +40 ( I1 + I2 ) =40 I1+ 60 I 2
Solving Simultaneous Equations
I 1=−0.143 A

I 2=0.429 A
I 3=−0.143+0.429=0.286 A
Remove RL Ohms = 10 Ohms resistor
EMF in the circuit = 12 V – 6V = 6V
Total circuit Resistance, RT ( R1∈series with R2 ) =6 Ohms+12 Ohms=18 Ohms
Current in the Circuit, I = 6
18 =0.333 A
Voltage appearing between XY:

V XY =EMFXY −Voltage across V 2
V XY =12− ( 12 x 0.333 )
V XY =12−4=8 V
Equivalent Voltage (Vs) = 8V
Equivalent Resistance (R equivalent) = R1 ∈¿ with R2
Requivalent = R1 x R2
R1 + R2
=6 x 12
6+12 =72
18 =4 Ohms
Therefore, Thevenin’s Equivalent circuit would consist of a voltage source of 8V and a series
resistance of 4Ω
V Thevenin =8 V
RThevenin =4 Ohms
By adding the RL Ohms = 10 Ohms resistor into the circuit:
The current flowing through RL;
I = V
R = 8 V
4 Ω+10 Ω = 8
14 =0.571 A
The voltage across RL
V =IR
V =0.571 X 10
V =5.71 V

b. Using Norton’s theorem for simplification of circuits, determine the current flowing in and the
voltage drop across Rl, the 6 Ω resistor in the network shown
To calculate the Nortons equivalent of the circuit above center 6Ω load resistor is removed first
and short out the terminals X and Y to give us the following circuit.
Break the circuit into two sides after shortening the 6 Ohms resistor as shown below:

I 1= 84
12 =7 Amp ,
I 2= 24
24 =1 Amp
Adding thetwo currents=I 1+I 2=7 A+1 A=8 Amps
The Equivalent Resistance (Rs)
12 Ω and 24 Ω in parallel
RT = R1 x R2
R1 + R2
= 12 x 24
12+24 =288
36 =8 Ω
Nortons equivalent circuit
Reconnecting the 6 Ohms resistor

Using 8A to determine the voltage across 6 Ohms resistor
By the use of current divider rule:
Current across 6 Ohms resistor = 8
8+6 x 8 A= 8
14 x 8 A=4.57 A
Voltage drop 6 Ohms resistor¿ 4.57 x 6=27.43 A

The first step is to split the circuit into two;
Remove the 84V power supply from the circuit;
Let RR=Resistance of circuit , R

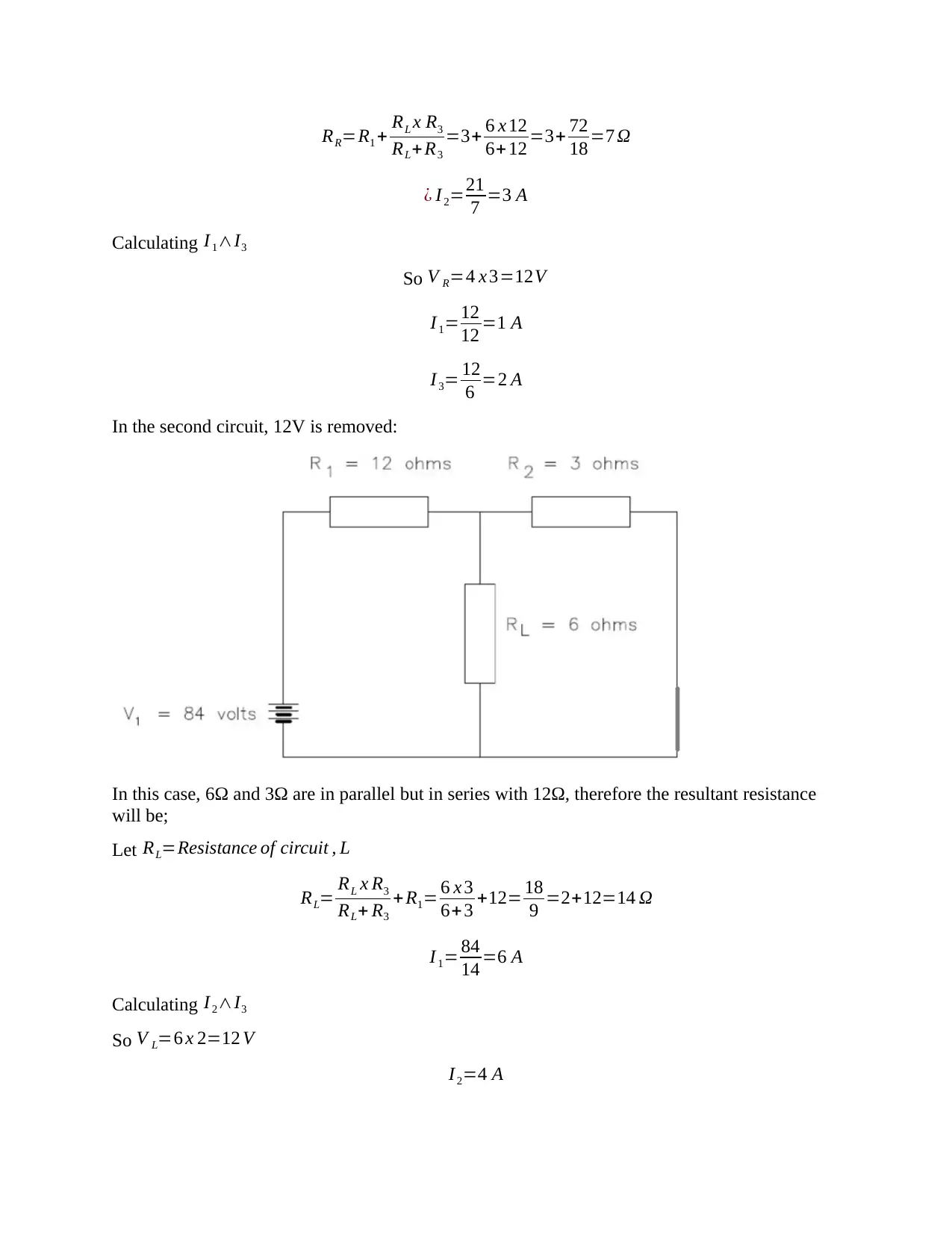
RR=R1 + RL x R3
RL+R3
=3+ 6 x 12
6+12 =3+ 72
18 =7 Ω
¿ I 2=21
7 =3 A
Calculating I 1∧I3
So V R=4 x 3=12V
I 1=12
12 =1 A
I 3= 12
6 =2 A
In the second circuit, 12V is removed:
In this case, 6Ω and 3Ω are in parallel but in series with 12Ω, therefore the resultant resistance
will be;
Let RL=Resistance of circuit , L
RL= RL x R3
RL+ R3
+ R1= 6 x 3
6+3 +12= 18
9 =2+12=14 Ω
I 1= 84
14 =6 A
Calculating I 2∧I3
So V L=6 x 2=12 V
I 2=4 A

I3=2 A
By reassembling the circuit;
From the Kirchhoff’s 1st Law: I 1+ I2 + I3 … … ..=0
I 1=6 A−1 A=5 A
I 2=4 A−3 A=1 A
I 3=2 A +2 A=4 A
Therefore, RL=4 A
Voltage across RL=4 x 6=24V
Task 3
The circuit below shows a method of retaining the memory of a ‘phone when a battery is
changed. Position 1 is the normal charging mode and position 2 is the reset of the ‘phone
memory by the discharge of the capacitor. The resistor R2 represents the ‘phone. The switch is in
position 1 for 10 seconds and then moved to position 2 for 5 seconds and then to position 1 for 5
seconds. Calculate;
a. The time constant for both switch positions.
b. Sketch rise and decay of the voltage across the capacitor and estimate the time required to
fully charge and completely discharge the capacitor
At switching position 1 (Capacitor charging); First 10 seconds
Time Constant, τ = R1 C = 10 x 103 x 100 x 10−6=1.0 s
At switching position 2 (Capacitor discharging) Next 5 seconds
Time Constant, τ = R2C = 5 x 103 x 100 x 10−6=0.5 s

At switching position 1 (Capacitor charging); Last 5 seconds
Time Constant, τ = R1 C = 10 x 103 x 100 x 10−6=1.0 s
During Charging (Position 1)
V C=V S {1−e( −t
RC )
}
At t = 0
V C=2 {1−e(−0
1 )
}=0
At t = 2
V C=2 {1−e(−2
1 )
}=1.729
At t = 4
V C=2 {1−e(−4
1 )
}=1.963
At t = 6
V C=2 {1−e(−6
1 )
}=1.995
At t = 8
V C=2 {1−e(−8
1 )
}=1.999
At t = 10
V C=2 {1−e(−10
1 )
}=2.0
Time Capacitor Voltage
0 0
2 1.729
4 1.963
6 1.995
8 1.999
10 2.0

Time required to fully charge = 5 Time constant
T = 5 x 1.0 = 5 seconds
During discharge
V C=V S {e( −t
RC )
}
At t = 0
V C=2 {e(−0
0.5 )
}=2
At t = 1
V C=2 { e
( −1
0.5 ) }=0.271
At t = 2
V C=2 {e(−2
0.5 )
}=0.0366
At t = 3

V C=2 {e(−3
0.5 )
}=0.00496
At t = 4
V C=2 {e(−4
0.5)
}=0.000671
At t = 5
V C=2 {e(−5
0.5 )
}=0.000091
Time Capacitor Voltage
0 2
1 0.271
2 0.0366
3 0.00496
4 0.000671
5 0.000091
Time required to fully discharge = 5 Time constant
T = 5 x 0.5 = 2.5 seconds
At switching position 1 (Capacitor charging); Last 5 seconds
V C=V S {1−e( −t
RC )
}

At t = 0
V C=2 {1−e(−0
1 )
}=0
At t = 1
V C=2 {1−e(−1
1 )
}=¿1.2642
At t = 2
V C=2 {1−e(−2
1 )
}=1.729
At t = 3
V C=2 {1−e(−3
1 )
}=1.9
At t = 4
V C=2 {1−e(−4
1 )
}=1.963
At t = 5
V C=2 {1−e(−5
1 )
}=1.9865
Time required to fully charge = 5 Time constant

T = 5 x 1.0 = 5 seconds
Task 4
The three diagrams below are complex waveforms.
a) Identify and describe each one.
b) Explain how they are produced from a pure sine wave
Triangular waveform: A triangular wave is a non-sinusoidal waveform named for its triangle
shape. They are continuous, piecewise linear, and periodic real function. By summing odd
harmonics of the fundamental while multiplying every odd by -1 which changes the phase by Π,
and multiplying one of the square of the mode number, n by the amplitude of the harmonics, the
resultant is triangular wave.
Just like square waves, triangular waves are produced from odd harmonics, but the higher
harmonics roll off much faster compared to the square waves.
The equation if summarized mathematically as:

Complex wave: This is a sine wave of various phases, amplitudes, and frequencies.
Complex waves can be produced by adding tow sine waves with frequency corresponding to the
fundamental and second harmonics from the harmonic series. The resultant waveform is a
complex wave with period equal to the period of the fundamental sine wave
Square wave: A square waveform is a non-sinusoidal periodic waveform in which there is
alternation of the amplitude at a steady frequency between fixed minimum and maximum values,
with similar duration at maximum and minimum.
A square wave may be produced from numerous sine waves at dissimilar frequencies. The sine
waves added in addition of fundamental frequency are known as harmonics. A square wave has
harmonics at fundamental frequency odd multiples.
As high harmonics are added, the outcome gets close to an ideal square wave which possesses
infinite harmonics.
sin ( angle ) + sin ( 3 x angle )
3 + sin ( 5 x angle )
5 + sin(7 x angle)
7 +. … ..

Inductive Reactance , XL=2 Π fL=2 Π x 50 x 0.15=47.13 Ω

Capacitive Reactance , Xc= 1
2 ΠfC = 1
2 Πx 50 x 100 x 10−6 =31.83 Ω
Circuit Impedance, Z= √ R2+ ( X L− XC )
, Z= √122+ ( 47.132−31.832 )
, Z= √ 144+234=19.4 Ω
Circuit Current, I
I = V S
Z = 100
19.4 =5.14 A
Voltages across RLC series circuit, V R ,V L , V C
V R=I x R=5.14 x 12=61.7 V
V L=I x X L=5.14 x 47.13=242.2 V
V C=I x XC =5.14 x 31.8=163.5V
Power factor of the circuit and Phase Angle θ
cos Φ= R
Z = 12
19.4 =0.619
cos−1 Φ=cos−1 0.619=51.8 lagging
Phasor diagram

Inductive Reactance , XL=ωL=2 Π fL=2 Π x 100 x 0.02=12.6 Ω
Capacitive Reactance , XC= 1
ωC = 1
2 ΠfC = 1
2 Πx 100 x 5 x 10−6 =318.3 Ω
Circuit Impedance,
Z= 1
√( 1
R )+ ( 1
XC
− 1
X L )2
Z= 1
√( 1
50 )+ ( 1
318.3 − 1
12.6 )2
¿ 1
√ ( 0.0004 +0.0058 ) = 1
0.0788 =12.7 Ω
Current through resistor; I R =V
R = 50
50 =1.0 A
Current through inductor; I L= V
XL
= 50
12.6 =3.9 A
Current through capacitor, I C= V
XC
= 50
318.3 =0.16 A
Total supply, Is = I S= √I R
2+ ( I L−IC ) = √ 12+ ( 3.9−0.16 ) 2=3.87 A

Conductance, G
G= 1
R = 1
50 =0.02 s
Inductive Susceptance, BC= 1
XC
= 1
318.3 =0.003 S
Admittance, Y = Y = 1
Z = 1
12.7 =0.078 s
Phase Angle, Φ between the resultant current and supply voltage
cos Φ= R
Z = 0.02
0.078 =0.256
Φ=cos−1 0.256=75o lag
Current Triangle
Admittance Triangle

Task 6 a) An ideal transformer has a turns ratio of 10:3 (Primary to secondary) and voltage
source of 250V on the primary winding. There is a resistance of 150Ω across the secondary
winding. Determine;
I. The electromotive force in the secondary winding.
II. The current in the secondary winding.
III. The current in the primary winding;
IV. The power input to the transformer. Note; An ideal transformer can be assumed to
have no losses.
N1
N 2
= V 1
V 2
=n=Turn ratio
n=250
V S
= 10
3
V S = 250 x 3
10 =75 V
E2=V 2=75 V
i. Electromotive force, E2 E2=75V
Power in secondary = V 2 I 2=I 2 R
ii. Current in secondary coil, I 2=V 2
R = 75
150 =0.5 A
Power in the Primary winding = Power in the secondary winding

Power , P=V 1 I1 =V 2 I 2
V 2 I2=75 x 0.5=37.5 W
iii.
Current ∈the primary winding , I1= P
V 1
=37.5
250 =0.15 A
iv.
Input Power V 1 I1=250 x 0.15=37.5 W
b) A transformer with a primary impedance of 1.2 KOhms has a circuit impedance of 100KOhms
connected to the secondary winding.
Determine the turns ratio of the transformer that will enable the maximum power to be
transmitted from the primary to the secondary winding from primary widnis.
Power in secondary = V 2 I 2
Power in the Primary = V 1 I 1
For maximum Power transfer; V 1 I1=V 2 I2
V 1 I1=V 2 I2
I 1
2 R1=I2
2 R2
I 1
2 x 1200=I2
2 x 100,000
I2
2
I1
2 = 100
1.2 =83.33333
I2
I1
= √ 83.33333=9.12
Since; V 1 I1=V 2 I2 =n
V 1
V 2
= I 2
I 1
=9.12
N = 10 turns

TECHNIQUES OF SOLVING RLC CIRCUITS
The techniques of solving RLC circuits using AC theory include using Simulink and Laplace
method
Laplace Transform
Laplace transform can be used in solving RLC circuits by providing the prediction of circuit
response. The first step when using this method is first developing the differential equation,
applying Laplace transformation and then solving the solution algebraically.
Simulink
The RLC circuits can also be solved by the use of MATLAB Simulink software which is first
installed and then using library browser in the software to key in the required parameters before
running the program.
BIBLIOGRAPHY
Ohira, T., 2016. Ideal Transformer [Enigmas, etc.]. s.l.:IEEE Microwave Magazine. Vol 17. pp. 102.
Seiger, H., 2012. The Confluence of Faraday's and Kirchoff's Laws in Bioelectrochemical Systems. s.l.:The
Scientific World Journal. Vol 2012. pp. 1-3.