ENGIN1002 Physics: Fluids Practical for Online Students
VerifiedAdded on 2023/03/31
|18
|2362
|472
AI Summary
This document provides a practical guide for ENGIN1002 Physics students to study fluids. It includes objectives, introduction, procedure, results and analysis, discussion, conclusion, and recommendations. The document also covers topics like flow meters, open channel flow, friction loss in pipes, and Reynolds number.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running Head: ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 1
ENGIN1002 Physics: Fluids Practical for Online Students
By(name)
Institutional Affiliation
ENGIN1002 Physics: Fluids Practical for Online Students
By(name)
Institutional Affiliation
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 2
Table of Contents
1. Objectives....................................................................................................................................1
2. Introduction..................................................................................................................................1
3. Procedure.....................................................................................................................................2
4. Results and Analysis....................................................................................................................3
5. Discussion....................................................................................................................................7
6. Conclusion...................................................................................................................................7
7. Recommendations........................................................................................................................7
8. References....................................................................................................................................7
List of Figures
Figure 1: Relationship between dynamic head and velocity...........................................................4
Figure 2: Relationship between Re and the friction factor, f..........................................................5
Figure 3: Relationship between Re and the loss coefficient, f.........................................................6
Table of Contents
1. Objectives....................................................................................................................................1
2. Introduction..................................................................................................................................1
3. Procedure.....................................................................................................................................2
4. Results and Analysis....................................................................................................................3
5. Discussion....................................................................................................................................7
6. Conclusion...................................................................................................................................7
7. Recommendations........................................................................................................................7
8. References....................................................................................................................................7
List of Figures
Figure 1: Relationship between dynamic head and velocity...........................................................4
Figure 2: Relationship between Re and the friction factor, f..........................................................5
Figure 3: Relationship between Re and the loss coefficient, f.........................................................6

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 1
Objectives
i) To determine the velocity of a fluid in a pipe using Bernoulli principle.
ii) To determine the friction coefficient f for a straight pipe for different flow rates
iii) To investigate the effect of an abrupt change in the pipe shape to the flow
characteristics of a fluid (water in this case) by determining the loss factor k.
Introduction
Some of the common flow meters used in measuring pipe flow include differential pressures
flowmeters including venture tube, rotameters, and orifice plates electromagnetic flow meter1.
These methods are however not applicable in open channel flows. In most cases flow
measurement in open channel is used in measurement of fluid height as the fluid passes through
an obstruction as a flume or a weir in the channel.
Weirs are of different types. The most common types include broad chested (rectangular) and
sharp-crested (either trapezoidal or triangular) (Mory, 2013). Sharp-crested weirs are used in the
measurement of discharge of smaller channels while broad-crested weirs are used in the
measurement of large canals and river’s channels (Monin & Yaglom, 2013).
In this case the flow rate is computed using the formula
Q=Cd 2
3 B √ ( 2 g ) h
3
2
Where;
Cd is the coefficient of discharge.
h is the height measured from the top of the weir to the water surface.
B is the width of the water channel.
g is the acceleration due to gravity = 9.81 m/s2
Therefore, it is easy to calculate the flow rate Q by measuring h.
1
Objectives
i) To determine the velocity of a fluid in a pipe using Bernoulli principle.
ii) To determine the friction coefficient f for a straight pipe for different flow rates
iii) To investigate the effect of an abrupt change in the pipe shape to the flow
characteristics of a fluid (water in this case) by determining the loss factor k.
Introduction
Some of the common flow meters used in measuring pipe flow include differential pressures
flowmeters including venture tube, rotameters, and orifice plates electromagnetic flow meter1.
These methods are however not applicable in open channel flows. In most cases flow
measurement in open channel is used in measurement of fluid height as the fluid passes through
an obstruction as a flume or a weir in the channel.
Weirs are of different types. The most common types include broad chested (rectangular) and
sharp-crested (either trapezoidal or triangular) (Mory, 2013). Sharp-crested weirs are used in the
measurement of discharge of smaller channels while broad-crested weirs are used in the
measurement of large canals and river’s channels (Monin & Yaglom, 2013).
In this case the flow rate is computed using the formula
Q=Cd 2
3 B √ ( 2 g ) h
3
2
Where;
Cd is the coefficient of discharge.
h is the height measured from the top of the weir to the water surface.
B is the width of the water channel.
g is the acceleration due to gravity = 9.81 m/s2
Therefore, it is easy to calculate the flow rate Q by measuring h.
1

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 2
Friction loss in pipes
In pipes, friction loss is concerned with the loss in head in a pipe as the fluid flow changes from
laminar to turbulent, for example by the introduction of a bent in a straight pipe. Pipe flow
studies are useful in determining the Reynolds number. To determine head loss, two manometers
are connected at different places along the length of the pipe. In the region with less turbulent
flow which can be considered laminar, the reading indicated by the manometer is lower than the
reading indicated by a manometer in a turbulent region which records high pressures (Institute et
al., 2012). The loss in head is due to effects of resistance to the motion of the fluid and is
expressed as a function of the loss factor f which is in turn related to the Reynolds number.
Head loss is given by the following equation:hL=f u2
2 g
L
D ,
Where,
hL is the head loss due to friction
u is the fluid velocity
L is the length of the pipe between the two manometers
D is the internal diameter of the pipe
In addition to the loss of head due to friction which is regarded as the major cause of head loss,
there are also other causes of head loss considered to be minor (Granger, 2012). These include
bends, open or partially closed valves, abrupt changes in contraction and expansion (Pletcher,
Tannehill, & Anderson, 2016). Head loss can also be expressed as a function of the loss factor k
as the equation below shows.
hL=k u2
2 g
Where,
k is the loss factor and u is the velocity.
2
Friction loss in pipes
In pipes, friction loss is concerned with the loss in head in a pipe as the fluid flow changes from
laminar to turbulent, for example by the introduction of a bent in a straight pipe. Pipe flow
studies are useful in determining the Reynolds number. To determine head loss, two manometers
are connected at different places along the length of the pipe. In the region with less turbulent
flow which can be considered laminar, the reading indicated by the manometer is lower than the
reading indicated by a manometer in a turbulent region which records high pressures (Institute et
al., 2012). The loss in head is due to effects of resistance to the motion of the fluid and is
expressed as a function of the loss factor f which is in turn related to the Reynolds number.
Head loss is given by the following equation:hL=f u2
2 g
L
D ,
Where,
hL is the head loss due to friction
u is the fluid velocity
L is the length of the pipe between the two manometers
D is the internal diameter of the pipe
In addition to the loss of head due to friction which is regarded as the major cause of head loss,
there are also other causes of head loss considered to be minor (Granger, 2012). These include
bends, open or partially closed valves, abrupt changes in contraction and expansion (Pletcher,
Tannehill, & Anderson, 2016). Head loss can also be expressed as a function of the loss factor k
as the equation below shows.
hL=k u2
2 g
Where,
k is the loss factor and u is the velocity.
2
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 3
The second part of this laboratory exercise helps us calculate the two unknowns, k and f and to
derive the Reynolds number. Reynolds number is given by the following equation
Re = ρVD
μ where,
V is the velocity of the fluid in m/s
D is the internal diameter of the pipe in m
μ is the dynamic viscosity in kg/ms
ρis the density of the fluid in kg/m3
The density and dynamic viscosity are obtained from moody charts for a given temperature.
Procedure
Part (i)
The dynamic and static heads were measured using a pitot tube at different points along the pipe
length and the results entered into an excel sheet.
Part (ii)
The head loss for a for a short section of the pipe (914 mm) was measured for different flow
rates for both a straight pipe and a pipe with a right angle bend and the results were recorded in
an excel sheet.
Results and Analysis
Task 1
Open Channel.
Determining velocity from pitot readings
From the formula h= v 2
2 g
3
The second part of this laboratory exercise helps us calculate the two unknowns, k and f and to
derive the Reynolds number. Reynolds number is given by the following equation
Re = ρVD
μ where,
V is the velocity of the fluid in m/s
D is the internal diameter of the pipe in m
μ is the dynamic viscosity in kg/ms
ρis the density of the fluid in kg/m3
The density and dynamic viscosity are obtained from moody charts for a given temperature.
Procedure
Part (i)
The dynamic and static heads were measured using a pitot tube at different points along the pipe
length and the results entered into an excel sheet.
Part (ii)
The head loss for a for a short section of the pipe (914 mm) was measured for different flow
rates for both a straight pipe and a pipe with a right angle bend and the results were recorded in
an excel sheet.
Results and Analysis
Task 1
Open Channel.
Determining velocity from pitot readings
From the formula h= v 2
2 g
3

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 4
The velocity is given by, v = √ h
2 g which can be approximated as v = √ h
51 m/s when h is in mm
For example when h = 11 mm, v = √ 11
51 = 0.4644 m/s
NB: the rest of the calculations are performed in excel
The flow rate is obtained from,
Q=Cd 2
3 B √ ( 2 g ) h
3
2
Q = 2∗0.8∗75
1000 √ 2∗9.81 ( h1.5 ) = 0.00158 m3/s
Determining the mean velocity
u = Q
A , where A = B* h, h is the static head and Q is constant.
For example with h 65 mm, A = ( 75
1000 )( 65
1000 ) = 0.004875 m2
u = 0.00158
0.004875 = 0.3241 m/s
The values for the two velocities are different. The mean velocity is lower than the velocity
obtained from pitot readings by about 0.1403 m/s which is relatively high. This is indicative of
errors in the experiment, probably the measured head h and the dimensions needed to calculate
the area A.
4
The velocity is given by, v = √ h
2 g which can be approximated as v = √ h
51 m/s when h is in mm
For example when h = 11 mm, v = √ 11
51 = 0.4644 m/s
NB: the rest of the calculations are performed in excel
The flow rate is obtained from,
Q=Cd 2
3 B √ ( 2 g ) h
3
2
Q = 2∗0.8∗75
1000 √ 2∗9.81 ( h1.5 ) = 0.00158 m3/s
Determining the mean velocity
u = Q
A , where A = B* h, h is the static head and Q is constant.
For example with h 65 mm, A = ( 75
1000 )( 65
1000 ) = 0.004875 m2
u = 0.00158
0.004875 = 0.3241 m/s
The values for the two velocities are different. The mean velocity is lower than the velocity
obtained from pitot readings by about 0.1403 m/s which is relatively high. This is indicative of
errors in the experiment, probably the measured head h and the dimensions needed to calculate
the area A.
4

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 5
The sum of Pressure head + dynamic head + static head should be conserved at all points.
Therefore since dynamic head = static head-pressure head, it follows that the sum of the pitot
reading and the static head should be a constant. As the calculations in excel sheet show, the sum
appears to vary at some points
0 2 4 6 8 10 12
0
2
4
6
8
10
12
A plot of dynamic head against velocity
velocity m/s
head (mm)
Figure 1: Relationship between dynamic head and velocity
Task 2: Pipe friction
Area of the pipe is given by: A = 22
7 r2, r = 13.6/2000 = 0.0068 m
Therefore A = 22
7 *0.00682 = 0.000145 m2
Determining velocity
From the continuity equation, A1v1 = A2v2 = Q
5
The sum of Pressure head + dynamic head + static head should be conserved at all points.
Therefore since dynamic head = static head-pressure head, it follows that the sum of the pitot
reading and the static head should be a constant. As the calculations in excel sheet show, the sum
appears to vary at some points
0 2 4 6 8 10 12
0
2
4
6
8
10
12
A plot of dynamic head against velocity
velocity m/s
head (mm)
Figure 1: Relationship between dynamic head and velocity
Task 2: Pipe friction
Area of the pipe is given by: A = 22
7 r2, r = 13.6/2000 = 0.0068 m
Therefore A = 22
7 *0.00682 = 0.000145 m2
Determining velocity
From the continuity equation, A1v1 = A2v2 = Q
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 6
For example, if volume = 860 mL and time = 6.9 s, Q = ( 860
1000 )∗0.001
6.9
= 0.0001246 m3/s
Therefore, v = Q
A = 0.0001246
0.000145 = 0.85957 m/s
The straight pipe
From the equation, hL=f u2
2 g
L
D from which,
f = 2 gD hL
u2 L
For example, if hL = 0.018 m and v = 0.8596 then f = 2∗9.81∗0.0136∗0.018
0.8596∗0.8596∗0.914 = 0.00711
Calculating Reynolds number
Re = ρVD
μ
At 15 degree Celsius, ρ=999.099 kg/m3, μ = 0.001139 kg/m.s
For a velocity of 0.8596 m/s, Re = 999.099∗0.8596∗0.0136
0.001139 = 10254.63
For a laminar flow, f = 64
R
In our case, for Re = 10254.63, f = 64
10254.63 = 0.00624 which is less than the value obtained
from experimental data of 0.00711 by a factor of 0.00087.
6
For example, if volume = 860 mL and time = 6.9 s, Q = ( 860
1000 )∗0.001
6.9
= 0.0001246 m3/s
Therefore, v = Q
A = 0.0001246
0.000145 = 0.85957 m/s
The straight pipe
From the equation, hL=f u2
2 g
L
D from which,
f = 2 gD hL
u2 L
For example, if hL = 0.018 m and v = 0.8596 then f = 2∗9.81∗0.0136∗0.018
0.8596∗0.8596∗0.914 = 0.00711
Calculating Reynolds number
Re = ρVD
μ
At 15 degree Celsius, ρ=999.099 kg/m3, μ = 0.001139 kg/m.s
For a velocity of 0.8596 m/s, Re = 999.099∗0.8596∗0.0136
0.001139 = 10254.63
For a laminar flow, f = 64
R
In our case, for Re = 10254.63, f = 64
10254.63 = 0.00624 which is less than the value obtained
from experimental data of 0.00711 by a factor of 0.00087.
6
ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 7
NB: the rest of the calculations are included in the excel sheet.
3.9 3.95 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4
0
0.005
0.01
0.015
0.02
0.025 A graph of f against log(Re)
Log(Re)
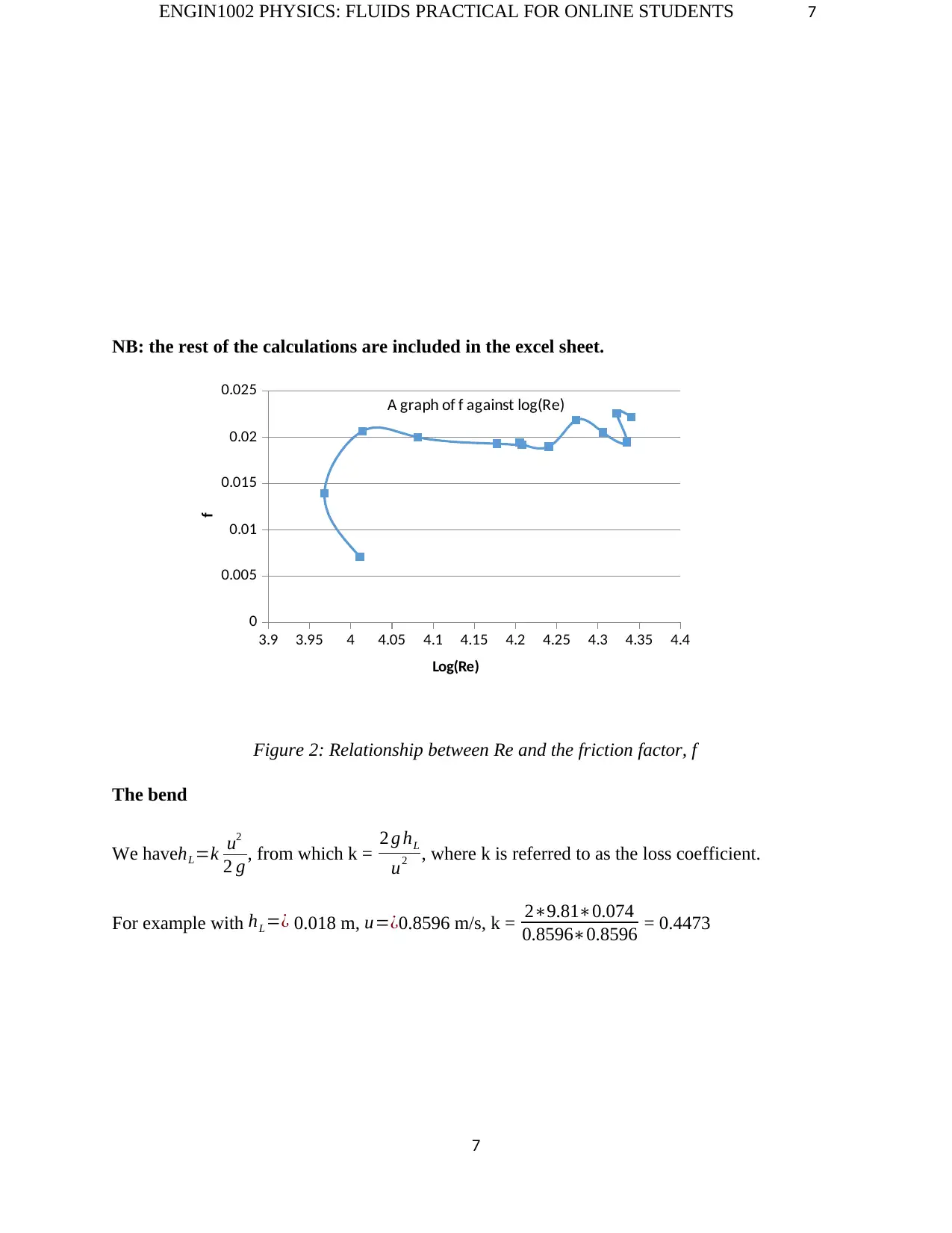
f
Figure 2: Relationship between Re and the friction factor, f
The bend
We havehL=k u2
2 g , from which k = 2 g hL
u2 , where k is referred to as the loss coefficient.
For example with hL=¿ 0.018 m, u=¿0.8596 m/s, k = 2∗9.81∗0.074
0.8596∗0.8596 = 0.4473
7
NB: the rest of the calculations are included in the excel sheet.
3.9 3.95 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4
0
0.005
0.01
0.015
0.02
0.025 A graph of f against log(Re)
Log(Re)
f
Figure 2: Relationship between Re and the friction factor, f
The bend
We havehL=k u2
2 g , from which k = 2 g hL
u2 , where k is referred to as the loss coefficient.
For example with hL=¿ 0.018 m, u=¿0.8596 m/s, k = 2∗9.81∗0.074
0.8596∗0.8596 = 0.4473
7
ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 8
3.9 3.95 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4
0
500
1000
1500
2000
2500
3000
3500
4000
A graph of k against log(Re)
k
log(Re)
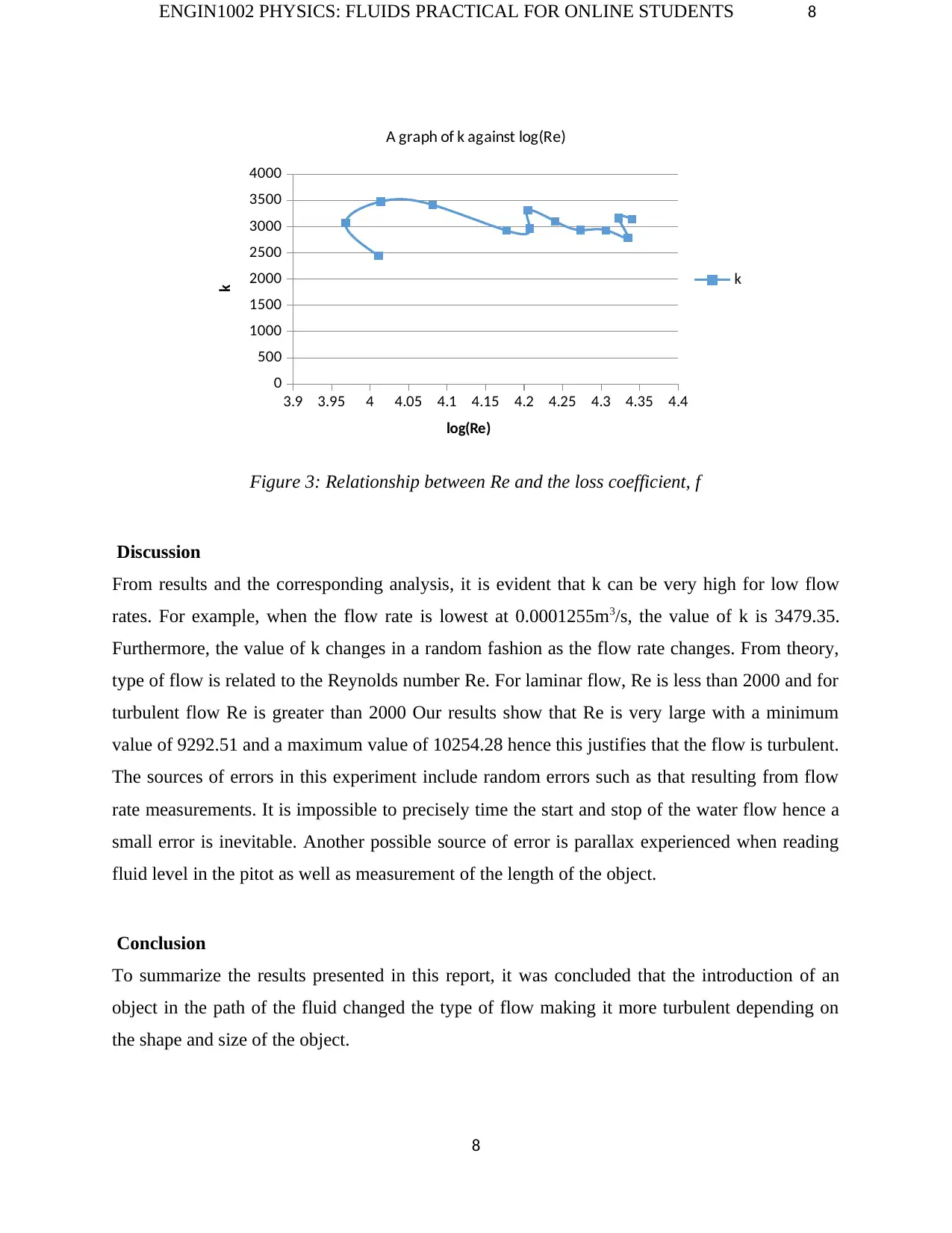
k
Figure 3: Relationship between Re and the loss coefficient, f
Discussion
From results and the corresponding analysis, it is evident that k can be very high for low flow
rates. For example, when the flow rate is lowest at 0.0001255m3/s, the value of k is 3479.35.
Furthermore, the value of k changes in a random fashion as the flow rate changes. From theory,
type of flow is related to the Reynolds number Re. For laminar flow, Re is less than 2000 and for
turbulent flow Re is greater than 2000 Our results show that Re is very large with a minimum
value of 9292.51 and a maximum value of 10254.28 hence this justifies that the flow is turbulent.
The sources of errors in this experiment include random errors such as that resulting from flow
rate measurements. It is impossible to precisely time the start and stop of the water flow hence a
small error is inevitable. Another possible source of error is parallax experienced when reading
fluid level in the pitot as well as measurement of the length of the object.
Conclusion
To summarize the results presented in this report, it was concluded that the introduction of an
object in the path of the fluid changed the type of flow making it more turbulent depending on
the shape and size of the object.
8
3.9 3.95 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4
0
500
1000
1500
2000
2500
3000
3500
4000
A graph of k against log(Re)
k
log(Re)
k
Figure 3: Relationship between Re and the loss coefficient, f
Discussion
From results and the corresponding analysis, it is evident that k can be very high for low flow
rates. For example, when the flow rate is lowest at 0.0001255m3/s, the value of k is 3479.35.
Furthermore, the value of k changes in a random fashion as the flow rate changes. From theory,
type of flow is related to the Reynolds number Re. For laminar flow, Re is less than 2000 and for
turbulent flow Re is greater than 2000 Our results show that Re is very large with a minimum
value of 9292.51 and a maximum value of 10254.28 hence this justifies that the flow is turbulent.
The sources of errors in this experiment include random errors such as that resulting from flow
rate measurements. It is impossible to precisely time the start and stop of the water flow hence a
small error is inevitable. Another possible source of error is parallax experienced when reading
fluid level in the pitot as well as measurement of the length of the object.
Conclusion
To summarize the results presented in this report, it was concluded that the introduction of an
object in the path of the fluid changed the type of flow making it more turbulent depending on
the shape and size of the object.
8
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 9
Recommendations
Several adjustments can be made to improve the accuracy of the results obtained in this
laboratory exercise. For instance, the experiment involving filling a bucket with water to
determine the flow rate can be improved by automating the process using automatic valves and
timers for more precise control.
References
Granger, R. A. (2012). Fluid Mechanics. North Chelmsford, MA: Courier Corporation.
Institute, T. P., Southerland, J. T., Boberg, J. S., Downey, M. S., Nakra, A., & Rabjohn, L. V.
(2012). McGlamry's Comprehensive Textbook of Foot and Ankle Surgery. Philadelphia,
PA: Lippincott Williams & Wilkins.
Monin, A. S., & Yaglom, A. M. (2013). Statistical fluid mechanics, volume II: mechanics of
turbulence. Courier Corporation.
Mory, M. (2013). Local Equations of Fluid Mechanics. Fluid Mechanics for Chemical
Engineering, 1-28.
Pletcher, R. H., Tannehill, J. C., & Anderson, D. (2016). Computational Fluid Mechanics and
Heat Transfer, Third Edition. Oxfordshire, England: Taylor & Francis.
9
Recommendations
Several adjustments can be made to improve the accuracy of the results obtained in this
laboratory exercise. For instance, the experiment involving filling a bucket with water to
determine the flow rate can be improved by automating the process using automatic valves and
timers for more precise control.
References
Granger, R. A. (2012). Fluid Mechanics. North Chelmsford, MA: Courier Corporation.
Institute, T. P., Southerland, J. T., Boberg, J. S., Downey, M. S., Nakra, A., & Rabjohn, L. V.
(2012). McGlamry's Comprehensive Textbook of Foot and Ankle Surgery. Philadelphia,
PA: Lippincott Williams & Wilkins.
Monin, A. S., & Yaglom, A. M. (2013). Statistical fluid mechanics, volume II: mechanics of
turbulence. Courier Corporation.
Mory, M. (2013). Local Equations of Fluid Mechanics. Fluid Mechanics for Chemical
Engineering, 1-28.
Pletcher, R. H., Tannehill, J. C., & Anderson, D. (2016). Computational Fluid Mechanics and
Heat Transfer, Third Edition. Oxfordshire, England: Taylor & Francis.
9

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 10
8. Appendices
Fluids practical 1: Open channel for Online students
Object is 150mm long, 25mm high at its maximum.
10
8. Appendices
Fluids practical 1: Open channel for Online students
Object is 150mm long, 25mm high at its maximum.
10

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 11
It is the same width of the channel, 75mm.
1. Flow measurement using rectangular weir:
Height of water above weir =
43mm
Cd of weir=0.8
2.Measurements over object:
Distance measurement: 0 is leading edge of object. + is downstream of this
Static head is depth from water surface, to channel bottom for distance <0 or > 150mm,
or to the object top surface for 0 < dist < 150mm.
Distanc
e
Pitot
tube Static head velocity1(u) area
Pitot
tube
mean
velocity
static
+pressure
head
mm mm mm mm
-1000 11 65 0.4644 0.004875 11 0.3241 76
11
It is the same width of the channel, 75mm.
1. Flow measurement using rectangular weir:
Height of water above weir =
43mm
Cd of weir=0.8
2.Measurements over object:
Distance measurement: 0 is leading edge of object. + is downstream of this
Static head is depth from water surface, to channel bottom for distance <0 or > 150mm,
or to the object top surface for 0 < dist < 150mm.
Distanc
e
Pitot
tube Static head velocity1(u) area
Pitot
tube
mean
velocity
static
+pressure
head
mm mm mm mm
-1000 11 65 0.4644 0.004875 11 0.3241 76
11
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
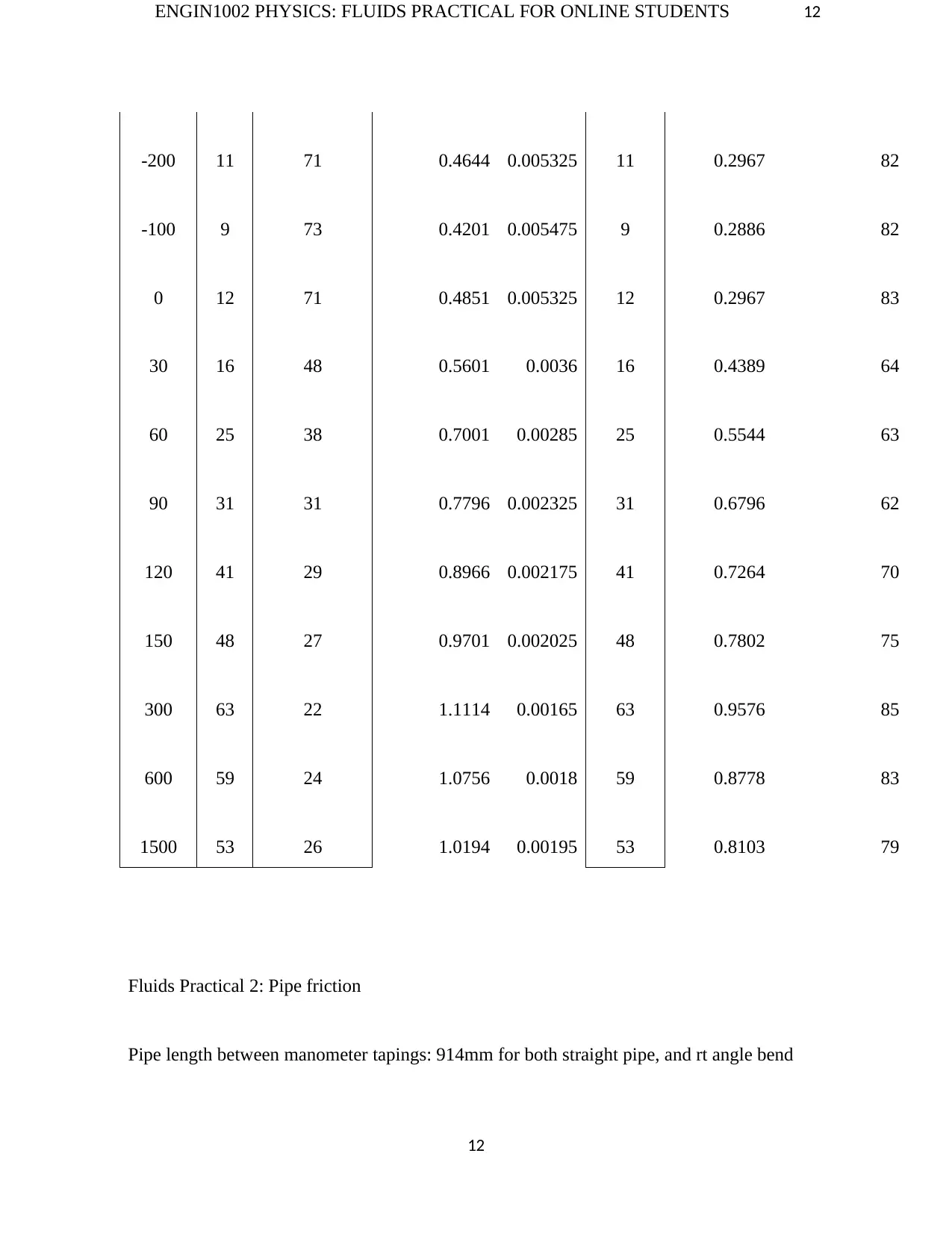
ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 12
-200 11 71 0.4644 0.005325 11 0.2967 82
-100 9 73 0.4201 0.005475 9 0.2886 82
0 12 71 0.4851 0.005325 12 0.2967 83
30 16 48 0.5601 0.0036 16 0.4389 64
60 25 38 0.7001 0.00285 25 0.5544 63
90 31 31 0.7796 0.002325 31 0.6796 62
120 41 29 0.8966 0.002175 41 0.7264 70
150 48 27 0.9701 0.002025 48 0.7802 75
300 63 22 1.1114 0.00165 63 0.9576 85
600 59 24 1.0756 0.0018 59 0.8778 83
1500 53 26 1.0194 0.00195 53 0.8103 79
Fluids Practical 2: Pipe friction
Pipe length between manometer tapings: 914mm for both straight pipe, and rt angle bend
12
-200 11 71 0.4644 0.005325 11 0.2967 82
-100 9 73 0.4201 0.005475 9 0.2886 82
0 12 71 0.4851 0.005325 12 0.2967 83
30 16 48 0.5601 0.0036 16 0.4389 64
60 25 38 0.7001 0.00285 25 0.5544 63
90 31 31 0.7796 0.002325 31 0.6796 62
120 41 29 0.8966 0.002175 41 0.7264 70
150 48 27 0.9701 0.002025 48 0.7802 75
300 63 22 1.1114 0.00165 63 0.9576 85
600 59 24 1.0756 0.0018 59 0.8778 83
1500 53 26 1.0194 0.00195 53 0.8103 79
Fluids Practical 2: Pipe friction
Pipe length between manometer tapings: 914mm for both straight pipe, and rt angle bend
12

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 13
Pipe ID 13.6mm
Material: drawn brass.
Volume
tim
e head loss head loss
straight pipe only bend + straight
milliliters sec mm mm
860 6.9 18 92
820
7.2
6 29 95
860
6.8
5 53 133
865 5.9 70 178
870
4.7
6 105 237
880
4.4
9 120 276
972 4.9 120 305
13
Pipe ID 13.6mm
Material: drawn brass.
Volume
tim
e head loss head loss
straight pipe only bend + straight
milliliters sec mm mm
860 6.9 18 92
820
7.2
6 29 95
860
6.8
5 53 133
865 5.9 70 178
870
4.7
6 105 237
880
4.4
9 120 276
972 4.9 120 305
13

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 14
9
900
4.2
6 138 336
960
4.2
1 185 370
1040
4.2
3 202 430
980
3.7
3 219 467
825
3.2
3 240 501
1030
3.8
7 256 540
flow rate
Velocity(m/
s) f Re log(Re) f log(Re) k
0.000124638 0.8596
0.00711
2 10254.27752
4.01090
5
0.00711
2
4.01090
5
2442.5256
6
0.000112948 0.7789
0.01395
3 9292.50788
3.96813
3
0.01395
3
3.96813
3
3070.9415
83
14
9
900
4.2
6 138 336
960
4.2
1 185 370
1040
4.2
3 202 430
980
3.7
3 219 467
825
3.2
3 240 501
1030
3.8
7 256 540
flow rate
Velocity(m/
s) f Re log(Re) f log(Re) k
0.000124638 0.8596
0.00711
2 10254.27752
4.01090
5
0.00711
2
4.01090
5
2442.5256
6
0.000112948 0.7789
0.01395
3 9292.50788
3.96813
3
0.01395
3
3.96813
3
3070.9415
83
14
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 15
0.000125547 0.8658
0.02063
9 10329.12626
4.01406
4
0.02063
9
4.01406
4
3479.3473
69
0.00014661 1.0111
0.01998
9 12062.01328 4.08142
0.01998
9 4.08142
3414.7270
48
0.000182773 1.2605
0.01929
3 15037.23567
4.17716
8
0.01929
3
4.17716
8
2925.2723
23
0.000195991 1.3517
0.01917
5 16124.71463
4.20749
2
0.01917
5
4.20749
2
2962.6651
07
0.00019479 1.3434
0.01941
2 16025.863
4.20482
1
0.01941
2
4.20482
1
3314.6105
22
0.000211268 1.4570
0.01897
8 17381.55459
4.24008
9
0.01897
8
4.24008
9
3104.0596
37
0.000228029 1.5726
0.02183
8 18760.51878
4.27324
5
0.02183
8
4.27324
5
2933.8726
3
0.000245863 1.6956
0.02051
1 20227.80127
4.30594
9
0.02051
1
4.30594
9
2933.0093
94
0.000262735 1.8120
0.01947
3 21615.88147
4.33477
3
0.01947
3
4.33477
3
2789.4185
83
0.000255418 1.7615
0.02258
1 21013.92281
4.32250
7
0.02258
1
4.32250
7
3166.3709
02
15
0.000125547 0.8658
0.02063
9 10329.12626
4.01406
4
0.02063
9
4.01406
4
3479.3473
69
0.00014661 1.0111
0.01998
9 12062.01328 4.08142
0.01998
9 4.08142
3414.7270
48
0.000182773 1.2605
0.01929
3 15037.23567
4.17716
8
0.01929
3
4.17716
8
2925.2723
23
0.000195991 1.3517
0.01917
5 16124.71463
4.20749
2
0.01917
5
4.20749
2
2962.6651
07
0.00019479 1.3434
0.01941
2 16025.863
4.20482
1
0.01941
2
4.20482
1
3314.6105
22
0.000211268 1.4570
0.01897
8 17381.55459
4.24008
9
0.01897
8
4.24008
9
3104.0596
37
0.000228029 1.5726
0.02183
8 18760.51878
4.27324
5
0.02183
8
4.27324
5
2933.8726
3
0.000245863 1.6956
0.02051
1 20227.80127
4.30594
9
0.02051
1
4.30594
9
2933.0093
94
0.000262735 1.8120
0.01947
3 21615.88147
4.33477
3
0.01947
3
4.33477
3
2789.4185
83
0.000255418 1.7615
0.02258
1 21013.92281
4.32250
7
0.02258
1
4.32250
7
3166.3709
02
15
ENGIN1002 PHYSICS: FLUIDS PRACTICAL FOR ONLINE STUDENTS 16
0.00026615 1.8355
0.02218
3 21896.86627
4.34038
2
0.02218
3
4.34038
2
3143.1876
64
16
0.00026615 1.8355
0.02218
3 21896.86627
4.34038
2
0.02218
3
4.34038
2
3143.1876
64
16
1 out of 18
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





