Econometrics and Business Statistics: Analysis of Interest Rates and Stock Prices

This study analyzes the relationship between interest rates and stock prices using econometrics and business statistics. The results show an inverse relationship between the two variables. The study includes a confidence interval for the population mean weight-loss, hypothesis testing, t-tests, scatter plots, and regression analysis. The study is based on data from S&P 500 and Treasury bills.

Running head: ECONOMETRICS AND BUSINESS STATISTICS
ECON634: Econometrics and Business Statistics
Name of the Student:
Macquarie University
Take-home Test

2ECONOMETRICS AND BUSINESS STATISTICS
Table of Contents
Question 1........................................................................................................................................3
Part 1a).........................................................................................................................................3
Part 1b).........................................................................................................................................3
Part 1c).........................................................................................................................................3
Part 1d).........................................................................................................................................4
Part 1e).........................................................................................................................................4
Part 1f).........................................................................................................................................5
Question 2........................................................................................................................................6
Part 2a).........................................................................................................................................6
Part 2b).........................................................................................................................................6
Part 2c).........................................................................................................................................8
Part 2d).......................................................................................................................................10
Part 2e).......................................................................................................................................11
Part 2f).......................................................................................................................................11
Question 3......................................................................................................................................12
Part 3a).......................................................................................................................................12
Part 3b).......................................................................................................................................12
Part 3c).......................................................................................................................................12
Part 3d).......................................................................................................................................14
Part 3e).......................................................................................................................................15
Question 4......................................................................................................................................15

3ECONOMETRICS AND BUSINESS STATISTICS
Question 1
Part 1a)
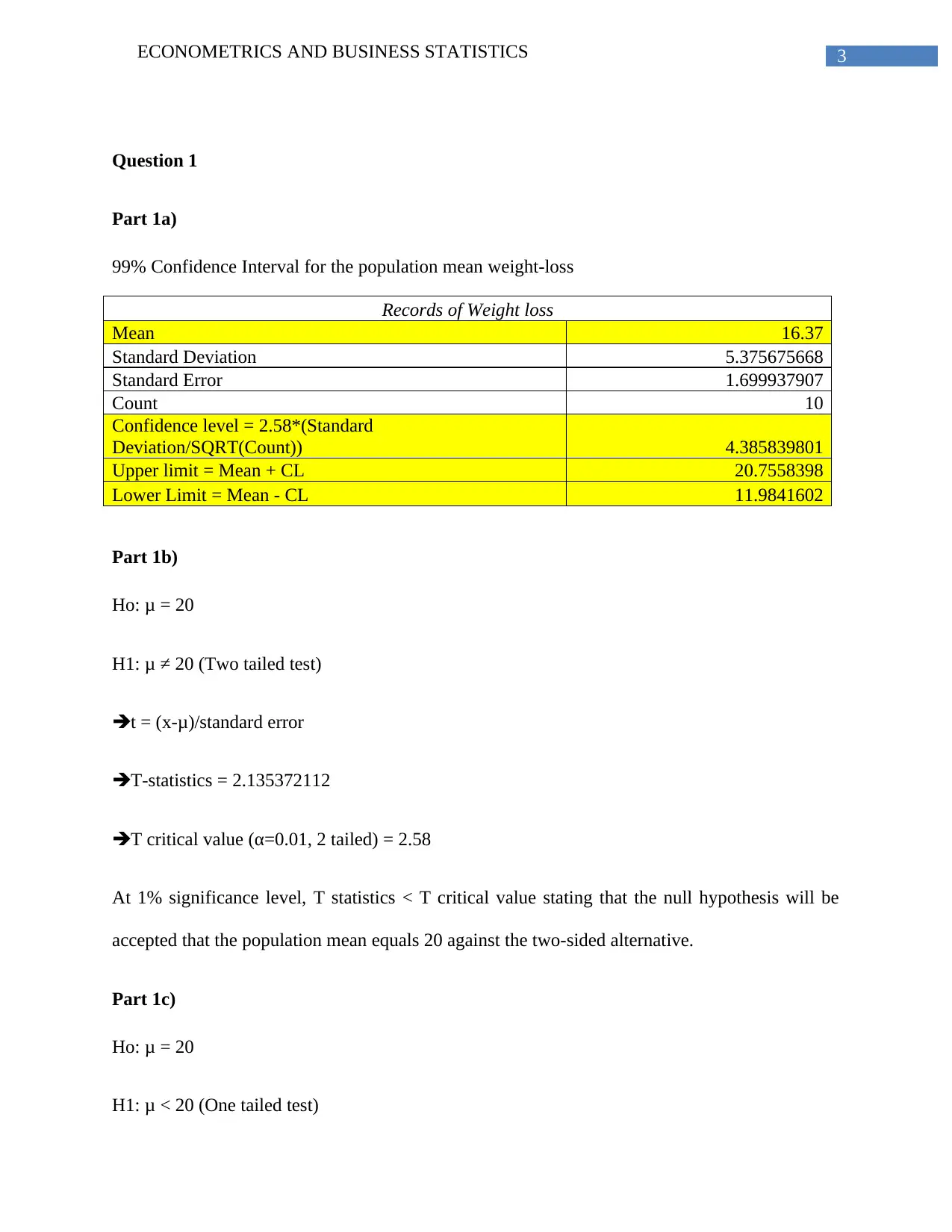
99% Confidence Interval for the population mean weight-loss
Records of Weight loss
Mean 16.37
Standard Deviation 5.375675668
Standard Error 1.699937907
Count 10
Confidence level = 2.58*(Standard
Deviation/SQRT(Count)) 4.385839801
Upper limit = Mean + CL 20.7558398
Lower Limit = Mean - CL 11.9841602
Part 1b)
Ho: μ = 20
H1: μ ≠ 20 (Two tailed test)
t = (x-μ)/standard error
T-statistics = 2.135372112
T critical value (α=0.01, 2 tailed) = 2.58
At 1% significance level, T statistics < T critical value stating that the null hypothesis will be
accepted that the population mean equals 20 against the two-sided alternative.
Part 1c)
Ho: μ = 20
H1: μ < 20 (One tailed test)

4ECONOMETRICS AND BUSINESS STATISTICS
t = (x-μ)/standard error
T statistics = 2.135372112
T critical value (α=0.05, one tailed) = 1.645
At 5% significance level, T statistics > T critical value stating that the null hypothesis will be
rejected that the population mean weight-loss is lower than 20 pounds at the 5% level against the
one-sided alternative hypothesis.
Part 1d)
P value results based on excel
=1-NORMDIST(X, Mean, Standard Deviation,TRUE)
=1-NORMDIST(20,16.74,1.699,TRUE)
p value = 0.016365313
Part 1e)
P value results based on excel
=1-NORMDIST(X, Mean, Standard Deviation,TRUE)
=1-NORMDIST(20,16.74,1.699,TRUE)
P value = 0.016365313
The calculated p-value of .0164 is the probability of committing a Type I Error (chance of
getting it wrong). A p-value of .016 is a considerable low probability of making a mistake, so it

5ECONOMETRICS AND BUSINESS STATISTICS
can be concluded that the averages are different and would not fall back to the null hypothesis of
population mean being 20.
Part 1f)
Ho: μ = 20
H1: μ < 20
t = (x-μ)/standard error
Standard error = 1.58113883 = 5/SQRT(10)
t statistics = 0.632455532
t critical value (α=0.05, one tailed) =1.645
Hence, null hypothesis accepted.
Critical value
=NORMINV(Probability (1-α),mean,Std dev)
=NORMINV(1-0.05,19,1.5811)
= 21.60074194
Beta
=NORMINV(1-0.05,19,1.5811)
=0.844326126 , this states that 84.32% failed to reject null hypothesis which is false, (false
negative)

6ECONOMETRICS AND BUSINESS STATISTICS
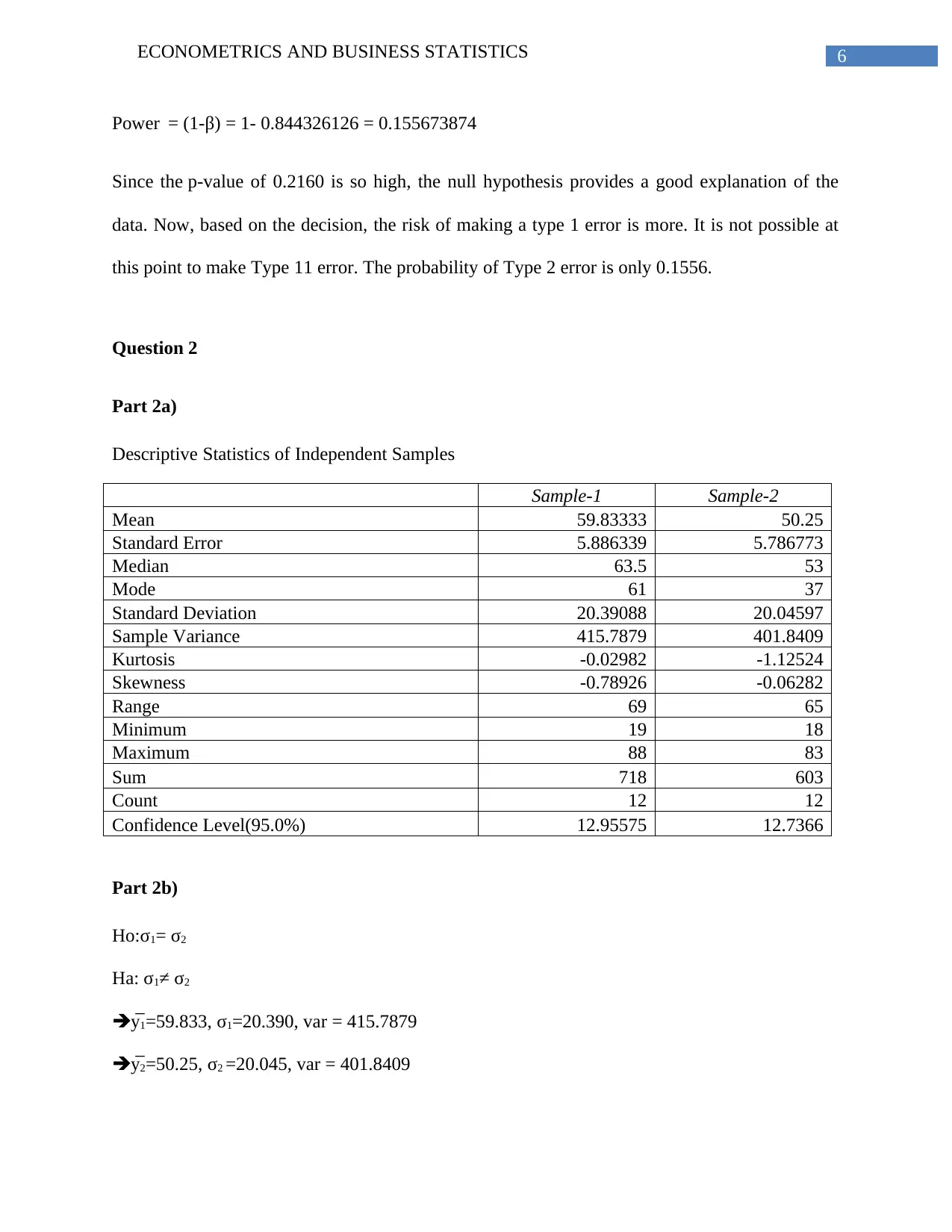
Power = (1-β) = 1- 0.844326126 = 0.155673874
Since the p-value of 0.2160 is so high, the null hypothesis provides a good explanation of the
data. Now, based on the decision, the risk of making a type 1 error is more. It is not possible at
this point to make Type 11 error. The probability of Type 2 error is only 0.1556.
Question 2
Part 2a)
Descriptive Statistics of Independent Samples
Sample-1 Sample-2
Mean 59.83333 50.25
Standard Error 5.886339 5.786773
Median 63.5 53
Mode 61 37
Standard Deviation 20.39088 20.04597
Sample Variance 415.7879 401.8409
Kurtosis -0.02982 -1.12524
Skewness -0.78926 -0.06282
Range 69 65
Minimum 19 18
Maximum 88 83
Sum 718 603
Count 12 12
Confidence Level(95.0%) 12.95575 12.7366
Part 2b)
Ho:σ1= σ2
Ha: σ1≠ σ2
y̅1=59.833, σ1=20.390, var = 415.7879
y̅2=50.25, σ2 =20.045, var = 401.8409

7ECONOMETRICS AND BUSINESS STATISTICS

8ECONOMETRICS AND BUSINESS STATISTICS
t-Test: Two-Sample Assuming Unequal Variances
Sample-1 Sample-2
Mean 59.83333333 50.25
Variance 415.7878788 401.8409091
Observations 12 12
Hypothesized Mean Difference 0
df 22
t Stat 1.160991741
P(T<=t) one-tail 0.129044121
t Critical one-tail 1.717144335
P(T<=t) two-tail 0.258088241
t Critical two-tail 2.073873058
Part 2c)

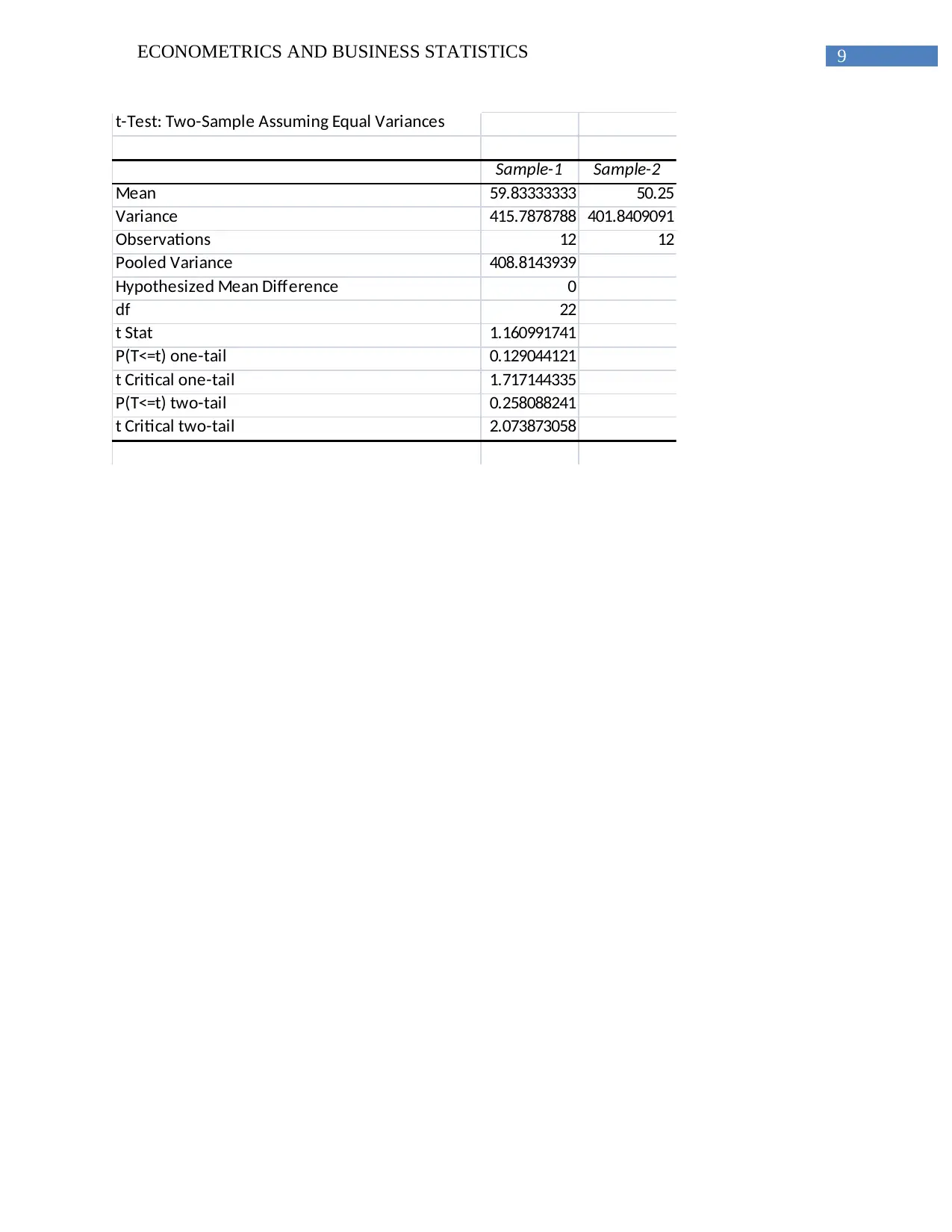
9ECONOMETRICS AND BUSINESS STATISTICS
t-Test: Two-Sample Assuming Equal Variances
Sample-1 Sample-2
Mean 59.83333333 50.25
Variance 415.7878788 401.8409091
Observations 12 12
Pooled Variance 408.8143939
Hypothesized Mean Difference 0
df 22
t Stat 1.160991741
P(T<=t) one-tail 0.129044121
t Critical one-tail 1.717144335
P(T<=t) two-tail 0.258088241
t Critical two-tail 2.073873058

10ECONOMETRICS AND BUSINESS STATISTICS
Part 2d)

11ECONOMETRICS AND BUSINESS STATISTICS
t-Test: Two-Sample Assuming Equal Variances
MP-Sam-1 MP-Sam-2
Mean 59.5 50.08333333
Variance 369 402.2651515
Observations 12 12
Pooled Variance 385.6325758
Hypothesized Mean Difference 0
df 22
t Stat 1.174589099
P(T<=t) one-tail 0.126358421
t Critical one-tail 1.717144335
P(T<=t) two-tail 0.252716842
t Critical two-tail 2.073873058
Part 2e)
The required condition for part c) and d) satisfied at the one tailed tests at df 22 at % significant
level which makes the results directional assuming equal variances for two samples whether
independent samples or matched samples.
Part 2f)
Independent sample t test for equal variances is undertaken because the two samples are taken
from different population. Also, where there is equal number of data points in both then equal
various test is considered whereas pairing of data is beneficial as it helps in analyzing the pre and
post variation for the same data with same data points. These differences occur because matched
pair is from the same population and independent t test is undertaken from two different
populations.

12ECONOMETRICS AND BUSINESS STATISTICS
Question 3
Part 3a)
As per the basic understanding, interest rates and stock prices have inverse relationship because
the high interest rates increases the costs of the companies that in turn lower the profits followed
by stock prices. However, the rising interest rate can be beneficial to reflect positive trends in the
economy.
Part 3b)
0 2 4 6 8 10 12 14 16
0
200
400
600
800
1000
1200
1400
1600
Scattergram between interest rates and stock
prices
Scattergram between interest
rates and stock prices
Interest Rates (T-Bill)
Stock Prices (S&P 500)
Yes, the scatter plot showing a downward increasing trend further justifies an inverse
relationship between interest rates and sock prices.
Part 3c)
Yt = β1 + β2Xt+ ε
S&P 500 = 1229.341 + 99.4014

13ECONOMETRICS AND BUSINESS STATISTICS
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.651891
R Square 0.424962
Adjusted R Square0.402845
Standard Error360.6937
Observations 28
ANOVA
df SS MS F Significance F
Regression 1 2499795 2499795 19.21442 0.000171
Residual 26 3382599 130100
Total 27 5882394
CoefficientsStandard Error t Stat P-value Lower 95%Upper 95%Lower 95.0%Upper 95.0%
Intercept 1229.341 148.4993 8.278433 9.26E-09 924.0967 1534.586 924.0967 1534.586
Tbill -99.4014 22.67665 -4.38343 0.000171 -146.014 -52.7889 -146.014 -52.7889
PROBABILITY OUTPUT
Percentile SP500
1.785714 118.78
5.357143 119.71
8.928571 128.05
12.5 160.41
16.07143 160.46
19.64286 186.84
23.21429 236.34
26.78571 265.79
30.35714 286.83
33.92857 322.84
37.5 334.59
41.07143 376.18
44.64286 415.74
48.21429 451.41
51.78571 460.42
55.35714 541.72
58.92857 670.5
62.5 873.43
66.07143 965.23
69.64286 993.94
73.21429 1085.5
76.78571 1130.65
80.35714 1194.18
83.92857 1207.23
87.5 1310.46
91.07143 1327.33
94.64286 1427.22
98.21429 1477.19
0
500
1000
1500
2000
0 20 40 60 80 100 120
SP500
Sample Percentile
Normal Probability Plot

14ECONOMETRICS AND BUSINESS STATISTICS
The R square came out as 0.4249962 which further states that around 42.49% variations are
explained by the independent variables in the model. The t statics is -43.83 highlighting inverse
relationship between the variables but being statistically valid as the p value is less than 0.05 at
5% significance level.
Part 3d)
As per the analysis, Treasury bill (interest rates) is the independent variable for the model that
affects the stock prices. Also, a change in Treasury bill would lead to 99.4014 units changes in
the stock prices results inversely. Yes, the sign of the slope coefficient is consistent with the
expectation of the given results assumed.
Part 3e)
Ho: The interest rates and stock prices have no significant relationship
H1: The interest rates and stock prices have inverse significant relationship (one tailed)
t = (x-μ)/standard error
Standard error = 22.676 = 5/SQRT(28)
t statistics = -4.38343
t critical value (α=0.05, one tailed) =-1.703
Hence, the null hypothesis will be rejected because the interest rates and stock prices have
inverse significant relationship.

15ECONOMETRICS AND BUSINESS STATISTICS
Question 4