University Flow Characteristics of Meters and Control Valve Experiment
VerifiedAdded on 2019/10/16
|15
|2811
|325
Practical Assignment
AI Summary
This assignment details an experiment investigating the flow characteristics of various air flow measuring and controlling devices. The experiment utilizes an air blower to generate flow through different devices including orifice plates, nozzles, Venturi tubes, Pitot tubes, and iris valves. The experimental procedure involves measuring the pressure drop across each device at different flow rates, which are controlled by adjusting the potentiometer setting of the air blower. The results section presents the data collected for each device, including manometer readings, calculated pressure drops, and air flow velocities. Sample calculations and graphs are provided to illustrate the relationships between flow rate and pressure drop. The analysis verifies theoretical predictions, such as the linear relationship between pipe velocity and the square root of the pressure drop for the orifice meter and nozzle. The Pitot tube experiment is used to determine the velocity profile within the pipe. The Iris valve experiment assesses the linear control of flow based on valve opening. This assignment offers valuable insights into fluid mechanics and experimental techniques.

Last Name 1
Name:
Professor:
Course:
Date: MMDDYYYY
Measurement of Flow Characteristics of Meters and Control Valve
Introduction: Fluid flow is measured and controlled by obstructing the flow with suitable
devices or modification of the internal diameter profile. Five types of devices are studied in
this experiment. Orifice plate, with central hole in a blind flange; Nozzle, like orifice plate
but the hole extended by a short pipe segment; Venturi tube, with converging and diverging
bells; Pitot tube, involving thin L-shaped tube with adjustable radial position, and Iris valve,
like adjustable diameter orifice plate; are studied using controlled delivery air blower. The air
flow creates a pressure drop across the device. The flow rate and corresponding pressure drop
are measured and plotted for the various devices.
Aim: To study pressure drop characteristics of various air flow measuring and controlling
devices and verify theoretical equations.
Experimental Procedure:
Equipment:
a) Two long and one short piece of PVC pipe sections of 84.6mm NB with flanges, a
pipe section with extensions and nut with bolts for connections.
b) An inlet element and an electric blower with potentiometer having settings
between 0 to 90. Air velocity in the pipe was made to vary linearly with
potentiometer setting.
c) 16 manometer panel. Small diameter columns: I and J, were to be used for Pitot
tube.
d) Anemometer to be placed at the centre of inlet element.
e) Flexible hoses for connecting to manometers.
f) Orifice plate and nozzle.
g) Venturi meter.
h) Pitot tube device with adjustable radial position.
i) Iris valve with adjustable opening diameter
Name:
Professor:
Course:
Date: MMDDYYYY
Measurement of Flow Characteristics of Meters and Control Valve
Introduction: Fluid flow is measured and controlled by obstructing the flow with suitable
devices or modification of the internal diameter profile. Five types of devices are studied in
this experiment. Orifice plate, with central hole in a blind flange; Nozzle, like orifice plate
but the hole extended by a short pipe segment; Venturi tube, with converging and diverging
bells; Pitot tube, involving thin L-shaped tube with adjustable radial position, and Iris valve,
like adjustable diameter orifice plate; are studied using controlled delivery air blower. The air
flow creates a pressure drop across the device. The flow rate and corresponding pressure drop
are measured and plotted for the various devices.
Aim: To study pressure drop characteristics of various air flow measuring and controlling
devices and verify theoretical equations.
Experimental Procedure:
Equipment:
a) Two long and one short piece of PVC pipe sections of 84.6mm NB with flanges, a
pipe section with extensions and nut with bolts for connections.
b) An inlet element and an electric blower with potentiometer having settings
between 0 to 90. Air velocity in the pipe was made to vary linearly with
potentiometer setting.
c) 16 manometer panel. Small diameter columns: I and J, were to be used for Pitot
tube.
d) Anemometer to be placed at the centre of inlet element.
e) Flexible hoses for connecting to manometers.
f) Orifice plate and nozzle.
g) Venturi meter.
h) Pitot tube device with adjustable radial position.
i) Iris valve with adjustable opening diameter
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Last Name 2
Details of individual experiment:
A) Nozzle and Orifice Plate:
1) The screws in the measuring flange were removed and 50mm ID orifice plate or
nozzle (in the direction of flow) were placed, aligned with the groove and re-fixed
together.
2) The two long pipes were separated by removing bolts and repositioned to
accommodate the measuring flange for orifice meter or nozzle. The parts were re-
bolted. Benches for intake pipe and fan were aligned using guiding pins and fixed
together using tow clamps. The bench rollers were then locked to prevent
unintended rolling of the benches.
3) The measuring points 15 and 16, were connected to the manometer panel by
rubber tubes, ensuring that the tubing remains unkinked.
4) The fan was started with potentiometer reading zero and manometer levels were
checked.
5) The manometer and Anemometer readings were taken for potentiometer positions
from 2 to 8 in steps of 1.
6) The manometer readings were converted to N/m2 and plotted with respect to
velocity measured using Anemometer.
B) Venturi tube:
1) The two long pipe sections were separated by removing clamps and adjusted to
accommodate the Venturi tube.
2) Hoses were connected to the measuring points 21, 22, 23, 24, 25 and 26, and inlets
on the manometer panel, ensuring no kinks in the hoses. The pipe diameters at the
measuring points were 21 (84.6 mm), 22 (71.8 mm), 23 (59 mm), 24 (66.8 mm),
25 (78.7 mm), and 26 (84.6 mm).
3) The fan was switched on, with the potentiometer set to zero. The levels of water in
the manometers were noted before starting the experiment.
4) For 5 different potentiometer settings (from 4 - 8), the differential manometer
readings (Δh, mm of water) were recorded and tabulated. The air flow velocities
were measured for each reading using the Anemometer provided.
C) Pitot Tube Experiment:
1) The Pitot tube was fixed between the intake pipe and pipe on the fan bench as
explained in A) above.
2) The hoses were used to connect measuring points 19 and 20, with the manometer
inlets I and J. As usual the hoses were connected without creating kinks.
3) The fan was switched on, with the potentiometer set to zero. Before starting the
experiment, the levels of manometers, I and J were checked.
4) For 6 different potentiometer settings (2 – 7 in steps of 1) and for each setting the
vertical distance (y) -40 to 40 mm in the steps of 20mm, the differential
manometer readings, Δh (mm of water), were recorded and tabulated.
D) Iris Control Valve Study:
1) The Iris valve was fixed like the measuring flange for orifice plate as described in
A) above.
2) Using the hoses, measuring points 17 and 18 were connected to the inlets on the
manometer panel, ensuring no kinks in the hoses.
Details of individual experiment:
A) Nozzle and Orifice Plate:
1) The screws in the measuring flange were removed and 50mm ID orifice plate or
nozzle (in the direction of flow) were placed, aligned with the groove and re-fixed
together.
2) The two long pipes were separated by removing bolts and repositioned to
accommodate the measuring flange for orifice meter or nozzle. The parts were re-
bolted. Benches for intake pipe and fan were aligned using guiding pins and fixed
together using tow clamps. The bench rollers were then locked to prevent
unintended rolling of the benches.
3) The measuring points 15 and 16, were connected to the manometer panel by
rubber tubes, ensuring that the tubing remains unkinked.
4) The fan was started with potentiometer reading zero and manometer levels were
checked.
5) The manometer and Anemometer readings were taken for potentiometer positions
from 2 to 8 in steps of 1.
6) The manometer readings were converted to N/m2 and plotted with respect to
velocity measured using Anemometer.
B) Venturi tube:
1) The two long pipe sections were separated by removing clamps and adjusted to
accommodate the Venturi tube.
2) Hoses were connected to the measuring points 21, 22, 23, 24, 25 and 26, and inlets
on the manometer panel, ensuring no kinks in the hoses. The pipe diameters at the
measuring points were 21 (84.6 mm), 22 (71.8 mm), 23 (59 mm), 24 (66.8 mm),
25 (78.7 mm), and 26 (84.6 mm).
3) The fan was switched on, with the potentiometer set to zero. The levels of water in
the manometers were noted before starting the experiment.
4) For 5 different potentiometer settings (from 4 - 8), the differential manometer
readings (Δh, mm of water) were recorded and tabulated. The air flow velocities
were measured for each reading using the Anemometer provided.
C) Pitot Tube Experiment:
1) The Pitot tube was fixed between the intake pipe and pipe on the fan bench as
explained in A) above.
2) The hoses were used to connect measuring points 19 and 20, with the manometer
inlets I and J. As usual the hoses were connected without creating kinks.
3) The fan was switched on, with the potentiometer set to zero. Before starting the
experiment, the levels of manometers, I and J were checked.
4) For 6 different potentiometer settings (2 – 7 in steps of 1) and for each setting the
vertical distance (y) -40 to 40 mm in the steps of 20mm, the differential
manometer readings, Δh (mm of water), were recorded and tabulated.
D) Iris Control Valve Study:
1) The Iris valve was fixed like the measuring flange for orifice plate as described in
A) above.
2) Using the hoses, measuring points 17 and 18 were connected to the inlets on the
manometer panel, ensuring no kinks in the hoses.

Last Name 3
3) The fan was switched on, with the potentiometer set to zero. The level of water in
the manometers was checked before starting the experiment.
4) The blower potentiometer settings from 2 to 6 in steps of 1 were used. For each
setting, readings were taken for 6 valve positions from 1 to 6. The readings were
recorded and tabulated.
3) The fan was switched on, with the potentiometer set to zero. The level of water in
the manometers was checked before starting the experiment.
4) The blower potentiometer settings from 2 to 6 in steps of 1 were used. For each
setting, readings were taken for 6 valve positions from 1 to 6. The readings were
recorded and tabulated.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Last Name 4
Results:
A) Nozzle and Orifice Flows:
Nozzle Characteristics
Potentiomete
r
∆h
(mm)
∆P
(N/m2)
sqrt(∆P
)
(N0.5/m)
Velocit
y (m/s)
2 4 39.2 6.3 1.4
3 8 78.5 8.9 2.1
4 15 147.2 12.1 2.8
5 23 225.6 15.0 3.5
6 33 323.7 18.0 4.2
7 46 451.3 21.2 5.0
8 63 618.0 24.9 6.0
∆h = Manometer Reading, ∆P = Manometer reading converted to Pa or N/m2, Velocity is as
measured by Anemometer.
Orifice Plate Characteristics:
Potentiometer
Setting
∆h
(mm)
∆P
(N/m2)
sqrt(∆P
)
(N0.5/m)
Velocity
(m/s)
2 4 39.2 6.3 1.2
3 9 88.3 9.4 1.9
4 16 157.0 12.5 2.5
5 23 225.6 15.0 3.1
6 35 343.4 18.5 3.8
7 48 470.9 21.7 4.4
8 64 627.8 25.1 5.1
Sample Calculations:
Conversion of (∆h) in mm WC to (∆P) in N/m2:
30 mm WC = (30 m/1000) * (1000 kg/m3) * (9.8 m/s2) = 294 N/m2 (or Pa).
Results:
A) Nozzle and Orifice Flows:
Nozzle Characteristics
Potentiomete
r
∆h
(mm)
∆P
(N/m2)
sqrt(∆P
)
(N0.5/m)
Velocit
y (m/s)
2 4 39.2 6.3 1.4
3 8 78.5 8.9 2.1
4 15 147.2 12.1 2.8
5 23 225.6 15.0 3.5
6 33 323.7 18.0 4.2
7 46 451.3 21.2 5.0
8 63 618.0 24.9 6.0
∆h = Manometer Reading, ∆P = Manometer reading converted to Pa or N/m2, Velocity is as
measured by Anemometer.
Orifice Plate Characteristics:
Potentiometer
Setting
∆h
(mm)
∆P
(N/m2)
sqrt(∆P
)
(N0.5/m)
Velocity
(m/s)
2 4 39.2 6.3 1.2
3 9 88.3 9.4 1.9
4 16 157.0 12.5 2.5
5 23 225.6 15.0 3.1
6 35 343.4 18.5 3.8
7 48 470.9 21.7 4.4
8 64 627.8 25.1 5.1
Sample Calculations:
Conversion of (∆h) in mm WC to (∆P) in N/m2:
30 mm WC = (30 m/1000) * (1000 kg/m3) * (9.8 m/s2) = 294 N/m2 (or Pa).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Last Name 5
Graphs:
5.0 10.0 15.0 20.0 25.0 30.0
0
1
2
3
4
5
6
7
f(x) = 0.236183661084411 x
A1) Nozzle Flow Characteristics
SQRT(DP in Pa)
Velocity in m/s
5.0 10.0 15.0 20.0 25.0 30.0
0
1
2
3
4
5
6
f(x) = 0.20332915291029 x
A2) Orifice Plate Flow Characteristics
SQRT(DP in Pa)
Velocity in m/s
Comments:
1) Nozzle: The points lie in a straight line and the constant of proportionality between
Pipe Velocity to Square root of DP is 0.24.
2) Orifice meter: The points lie in a straight line and the constant correlating the Square
root of ∆P across the meter to Pipe Velocity is 0.2. The constant is lower than the one
for nozzle, as pressure drop is lower for the nozzle.
u0 = CD
√1−β4 ∗
√ 2∗gc∗( pa− pb )
ρ
(McCabe and Smith, p. 219).
Where, CD is constant for the given meter, β is ratio of orifice diameter to pipe
diameter, ρ is density of air and gc is unity in SI units.
Graphs:
5.0 10.0 15.0 20.0 25.0 30.0
0
1
2
3
4
5
6
7
f(x) = 0.236183661084411 x
A1) Nozzle Flow Characteristics
SQRT(DP in Pa)
Velocity in m/s
5.0 10.0 15.0 20.0 25.0 30.0
0
1
2
3
4
5
6
f(x) = 0.20332915291029 x
A2) Orifice Plate Flow Characteristics
SQRT(DP in Pa)
Velocity in m/s
Comments:
1) Nozzle: The points lie in a straight line and the constant of proportionality between
Pipe Velocity to Square root of DP is 0.24.
2) Orifice meter: The points lie in a straight line and the constant correlating the Square
root of ∆P across the meter to Pipe Velocity is 0.2. The constant is lower than the one
for nozzle, as pressure drop is lower for the nozzle.
u0 = CD
√1−β4 ∗
√ 2∗gc∗( pa− pb )
ρ
(McCabe and Smith, p. 219).
Where, CD is constant for the given meter, β is ratio of orifice diameter to pipe
diameter, ρ is density of air and gc is unity in SI units.

Last Name 6
Now by mass balance, u0 = V*β, where V is undisturbed velocity in the pipe and u0 is
orifice exit velocity.
Therefore, V is proportional to sqrt(pa – pb) or √∆P.
This requires, plot of √∆P versus V to be a straight line for orifice meter. The
experiment verifies the theoretical prediction.
Now by mass balance, u0 = V*β, where V is undisturbed velocity in the pipe and u0 is
orifice exit velocity.
Therefore, V is proportional to sqrt(pa – pb) or √∆P.
This requires, plot of √∆P versus V to be a straight line for orifice meter. The
experiment verifies the theoretical prediction.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Last Name 7
B) Venturi Tube Characteristics:
Potentiomet
er
Measurin
g Point
Id
∆h
(mm)
∆P
(N/m2)
sqrt(∆
P)
(
N0.5/m)
Velocit
y (m/s)
4 22 12 117.7 10.8 2.6
4 23 27 264.9 16.3 2.6
4 24 13 127.5 11.3 2.6
4 25 10 98.1 9.9 2.6
4 26 9 88.3 9.4 2.6
5 22 9 88.3 9.4 3.4
5 23 34 333.5 18.3 3.4
5 24 20 196.2 14.0 3.4
5 25 9 88.3 9.4 3.4
5 26 5 49.1 7.0 3.4
6 22 14 137.3 11.7 4.2
6 23 50 490.5 22.1 4.2
6 24 30 294.3 17.2 4.2
6 25 15 147.2 12.1 4.2
6 26 9 88.3 9.4 4.2
7 22 19 186.4 13.7 5.1
7 23 74 725.9 26.9 5.1
7 24 40 392.4 19.8 5.1
7 25 18 176.6 13.3 5.1
7 26 11 107.9 10.4 5.1
8 22 27 264.9 16.3 5.9
8 23 100 981.0 31.3 5.9
8 24 56 549.4 23.4 5.9
8 25 25 245.3 15.7 5.9
8 26 14 137.3 11.7 5.9
B) Venturi Tube Characteristics:
Potentiomet
er
Measurin
g Point
Id
∆h
(mm)
∆P
(N/m2)
sqrt(∆
P)
(
N0.5/m)
Velocit
y (m/s)
4 22 12 117.7 10.8 2.6
4 23 27 264.9 16.3 2.6
4 24 13 127.5 11.3 2.6
4 25 10 98.1 9.9 2.6
4 26 9 88.3 9.4 2.6
5 22 9 88.3 9.4 3.4
5 23 34 333.5 18.3 3.4
5 24 20 196.2 14.0 3.4
5 25 9 88.3 9.4 3.4
5 26 5 49.1 7.0 3.4
6 22 14 137.3 11.7 4.2
6 23 50 490.5 22.1 4.2
6 24 30 294.3 17.2 4.2
6 25 15 147.2 12.1 4.2
6 26 9 88.3 9.4 4.2
7 22 19 186.4 13.7 5.1
7 23 74 725.9 26.9 5.1
7 24 40 392.4 19.8 5.1
7 25 18 176.6 13.3 5.1
7 26 11 107.9 10.4 5.1
8 22 27 264.9 16.3 5.9
8 23 100 981.0 31.3 5.9
8 24 56 549.4 23.4 5.9
8 25 25 245.3 15.7 5.9
8 26 14 137.3 11.7 5.9
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Last Name 8
2 2.5 3 3.5 4 4.5 5 5.5 6 6.5
0
5
10
15
20
25
30
35
B) Venturi Tube Flow Characteristics
22 23 24 25 26
Velocity in m/s
SQRT(DP in Pa)
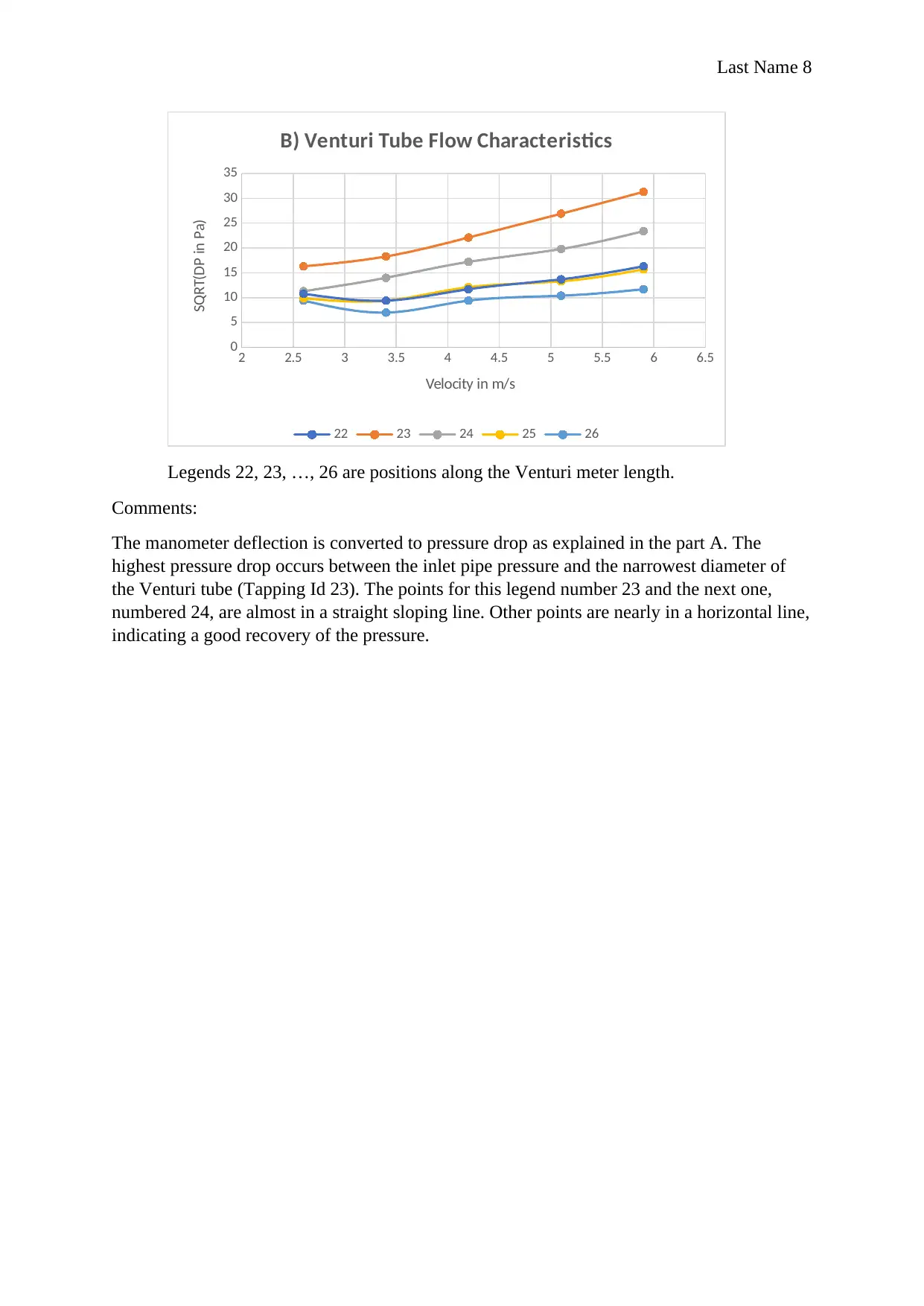
Legends 22, 23, …, 26 are positions along the Venturi meter length.
Comments:
The manometer deflection is converted to pressure drop as explained in the part A. The
highest pressure drop occurs between the inlet pipe pressure and the narrowest diameter of
the Venturi tube (Tapping Id 23). The points for this legend number 23 and the next one,
numbered 24, are almost in a straight sloping line. Other points are nearly in a horizontal line,
indicating a good recovery of the pressure.
2 2.5 3 3.5 4 4.5 5 5.5 6 6.5
0
5
10
15
20
25
30
35
B) Venturi Tube Flow Characteristics
22 23 24 25 26
Velocity in m/s
SQRT(DP in Pa)
Legends 22, 23, …, 26 are positions along the Venturi meter length.
Comments:
The manometer deflection is converted to pressure drop as explained in the part A. The
highest pressure drop occurs between the inlet pipe pressure and the narrowest diameter of
the Venturi tube (Tapping Id 23). The points for this legend number 23 and the next one,
numbered 24, are almost in a straight sloping line. Other points are nearly in a horizontal line,
indicating a good recovery of the pressure.

Last Name 9
C) Pitot Tube Study of Velocity Profile:
Potentiomet
er
∆h
(mm)
∆P
(N/m2)
sqrt(∆
P)
(
N0.5/m)
Vertica
l
Distanc
e (mm)
Velocit
y x
Consta
nt
2 0 0.0 0.0 -40 0.0
2 1 9.8 3.1 -20 3.1
2 1 9.8 3.1 0 3.1
2 1 9.8 3.1 20 3.1
2 0 0.0 0.0 40 0.0
3 1 9.8 3.1 -40 3.1
3 3 29.4 5.4 -20 5.4
3 3 29.4 5.4 0 5.4
3 3 29.4 5.4 20 5.4
3 1 9.8 3.1 40 3.1
4 3 29.4 5.4 -40 5.4
4 7 68.7 8.3 -20 8.3
4 8 78.5 8.9 0 8.9
4 8 78.5 8.9 20 8.9
4 4 39.2 6.3 40 6.3
5 4 39.2 6.3 -40 6.3
5 10 98.1 9.9 -20 9.9
5 12 117.7 10.8 0 10.8
5 13 127.5 11.3 20 11.3
5 6 58.9 7.7 40 7.7
6 8 78.5 8.9 -40 8.9
6 19 186.4 13.7 -20 13.7
6 20 196.2 14.0 0 14.0
6 20 196.2 14.0 20 14.0
6 7 68.7 8.3 40 8.3
7 13 127.5 11.3 -40 11.3
7 28 274.7 16.6 -20 16.6
7 33 323.7 18.0 0 18.0
7 34 333.5 18.3 20 18.3
7 15 147.2 12.1 40 12.1
C) Pitot Tube Study of Velocity Profile:
Potentiomet
er
∆h
(mm)
∆P
(N/m2)
sqrt(∆
P)
(
N0.5/m)
Vertica
l
Distanc
e (mm)
Velocit
y x
Consta
nt
2 0 0.0 0.0 -40 0.0
2 1 9.8 3.1 -20 3.1
2 1 9.8 3.1 0 3.1
2 1 9.8 3.1 20 3.1
2 0 0.0 0.0 40 0.0
3 1 9.8 3.1 -40 3.1
3 3 29.4 5.4 -20 5.4
3 3 29.4 5.4 0 5.4
3 3 29.4 5.4 20 5.4
3 1 9.8 3.1 40 3.1
4 3 29.4 5.4 -40 5.4
4 7 68.7 8.3 -20 8.3
4 8 78.5 8.9 0 8.9
4 8 78.5 8.9 20 8.9
4 4 39.2 6.3 40 6.3
5 4 39.2 6.3 -40 6.3
5 10 98.1 9.9 -20 9.9
5 12 117.7 10.8 0 10.8
5 13 127.5 11.3 20 11.3
5 6 58.9 7.7 40 7.7
6 8 78.5 8.9 -40 8.9
6 19 186.4 13.7 -20 13.7
6 20 196.2 14.0 0 14.0
6 20 196.2 14.0 20 14.0
6 7 68.7 8.3 40 8.3
7 13 127.5 11.3 -40 11.3
7 28 274.7 16.6 -20 16.6
7 33 323.7 18.0 0 18.0
7 34 333.5 18.3 20 18.3
7 15 147.2 12.1 40 12.1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Last Name 10
Legends 2, 3, …, 7 are the potentiometer settings for the blower.
Comments:
Bernoulli’s equation gives, P + ρgZ + ρV2/2 = constant along a flow-line (McCabe
and Smith, p. 72). As the pressure is constant in a vertical line and neglecting head
due to air column gravity, the reading of the Pitot tube manometer is ρV2/2. Thus, V is
proportional to the square root of water column head in the manometer. The plot of Z
vs V would be therefore, qualitatively similar to Z vs square root of manometer
reading.
The manometer readings can be converted to SI units as indicated in part A above.
The velocity profile is approximately flat in the central region, tapering to zero at the
pipe wall (+/- 42.3 mm). The velocity in the upper region of the centre appears to be
higher than the corresponding velocity in the lower region. This may be due to
position of the blower impeller with respect to the centre line of the discharge pipe,
which allows preferred movement of air in the upper region of pipe.
0 5 10 15 20
-50
-40
-30
-20
-10
0
10
20
30
40
50
Velocity
Radial
Distance in
mm
2
3
4
5
6
7
Legends 2, 3, …, 7 are the potentiometer settings for the blower.
Comments:
Bernoulli’s equation gives, P + ρgZ + ρV2/2 = constant along a flow-line (McCabe
and Smith, p. 72). As the pressure is constant in a vertical line and neglecting head
due to air column gravity, the reading of the Pitot tube manometer is ρV2/2. Thus, V is
proportional to the square root of water column head in the manometer. The plot of Z
vs V would be therefore, qualitatively similar to Z vs square root of manometer
reading.
The manometer readings can be converted to SI units as indicated in part A above.
The velocity profile is approximately flat in the central region, tapering to zero at the
pipe wall (+/- 42.3 mm). The velocity in the upper region of the centre appears to be
higher than the corresponding velocity in the lower region. This may be due to
position of the blower impeller with respect to the centre line of the discharge pipe,
which allows preferred movement of air in the upper region of pipe.
0 5 10 15 20
-50
-40
-30
-20
-10
0
10
20
30
40
50
Velocity
Radial
Distance in
mm
2
3
4
5
6
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Last Name 11
D) Iris Diaphragm Valve Characteristics:
Potentiomet
er
Setting
∆h
(mm)
∆P
(N/
m2)
Air
Flow
(d
m3/s)
%Valve
Opening
Diamete
r
2 3 29.4 10 53.8
2 7 68.6 18 59.4
2 8 78.4 28 68.8
2 4 39.2 28 76.3
2 4 39.2 36 85.0
2 4 39.2 50 92.5
3 7 68.6 15 53.8
3 8 78.4 21 59.4
3 7 68.6 28 68.8
3 9 88.2 40 76.3
3 8 78.4 50 85.0
3 7 68.6 68 92.5
4 14 137.2 21 53.8
4 15 147.0 30 59.4
4 15 147.0 32 68.8
4 15 147.0 52 76.3
4 20 196.0 78 85.0
4 13 127.4 90 92.5
5 22 215.6 25 53.8
5 23 225.4 34 59.4
5 24 235.2 48 68.8
5 25 245.0 64 76.3
5 24 235.2 85 85.0
5 20 196.0 110 92.5
6 33 323.4 32 53.8
6 34 333.2 42 59.4
6 35 343.0 60 68.8
6 38 372.4 80 76.3
6 36 352.8 100 85.0
6 30 294.0 140 92.5
D) Iris Diaphragm Valve Characteristics:
Potentiomet
er
Setting
∆h
(mm)
∆P
(N/
m2)
Air
Flow
(d
m3/s)
%Valve
Opening
Diamete
r
2 3 29.4 10 53.8
2 7 68.6 18 59.4
2 8 78.4 28 68.8
2 4 39.2 28 76.3
2 4 39.2 36 85.0
2 4 39.2 50 92.5
3 7 68.6 15 53.8
3 8 78.4 21 59.4
3 7 68.6 28 68.8
3 9 88.2 40 76.3
3 8 78.4 50 85.0
3 7 68.6 68 92.5
4 14 137.2 21 53.8
4 15 147.0 30 59.4
4 15 147.0 32 68.8
4 15 147.0 52 76.3
4 20 196.0 78 85.0
4 13 127.4 90 92.5
5 22 215.6 25 53.8
5 23 225.4 34 59.4
5 24 235.2 48 68.8
5 25 245.0 64 76.3
5 24 235.2 85 85.0
5 20 196.0 110 92.5
6 33 323.4 32 53.8
6 34 333.2 42 59.4
6 35 343.0 60 68.8
6 38 372.4 80 76.3
6 36 352.8 100 85.0
6 30 294.0 140 92.5

Last Name 12
20 30 40 50 60 70 80
0
20
40
60
80
100
120
140
160
E) Iris Valve Characteristics
2 3 4 5 6
% Open diameter
Flow Rate in lit/s
Legends 2, 3, …, 6 are potentiometer settings for the blower.
Sample Calculations:
1) Calculation of % Open Diameter in Iris valve:
For position 2 of the valve,
d = 47.5 mm. Fully open diameter = 80 mm.
Therefore, % open diameter = 47.5/80 = 59%.
2) Calculation of Flow rate in Iris Valve:
For potentiometer setting of 6 and the iris valve position of 5, ∆h = 36 mm.
As explained in 1) above, 36 mm WC = (36*9.8) = 353 Pa.
For line number 5 at 300 Pa, flow rate is about 95 dm3/s. So, using judgement, for 353
Pa, the flow rate would be close to 100 dm3/s.
Comments:
The % flow-rate is generally falling in a straight line with respect to % open diameter.
The variation is due to estimating velocity from nomogram. Thus, the Iris valve
controls the flow linearly with respect to % open diameter.
20 30 40 50 60 70 80
0
20
40
60
80
100
120
140
160
E) Iris Valve Characteristics
2 3 4 5 6
% Open diameter
Flow Rate in lit/s
Legends 2, 3, …, 6 are potentiometer settings for the blower.
Sample Calculations:
1) Calculation of % Open Diameter in Iris valve:
For position 2 of the valve,
d = 47.5 mm. Fully open diameter = 80 mm.
Therefore, % open diameter = 47.5/80 = 59%.
2) Calculation of Flow rate in Iris Valve:
For potentiometer setting of 6 and the iris valve position of 5, ∆h = 36 mm.
As explained in 1) above, 36 mm WC = (36*9.8) = 353 Pa.
For line number 5 at 300 Pa, flow rate is about 95 dm3/s. So, using judgement, for 353
Pa, the flow rate would be close to 100 dm3/s.
Comments:
The % flow-rate is generally falling in a straight line with respect to % open diameter.
The variation is due to estimating velocity from nomogram. Thus, the Iris valve
controls the flow linearly with respect to % open diameter.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





