Comprehensive Report: Quantitative Analysis of UK Social Attitudes

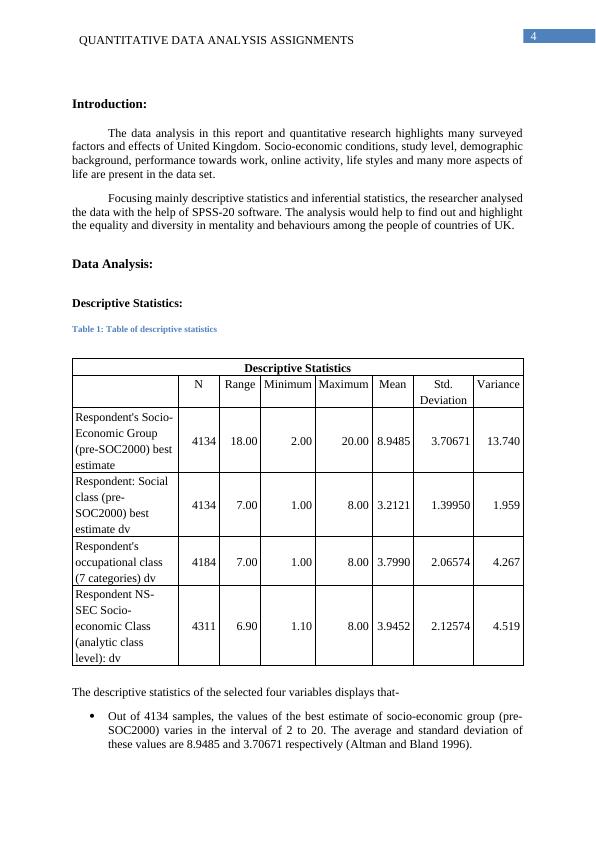
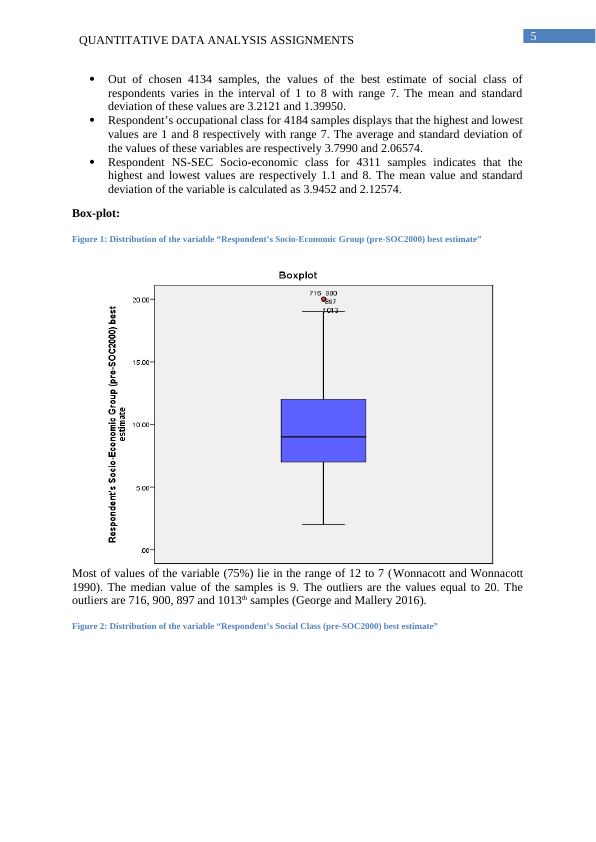
This report presents a quantitative data analysis of the UK Social Attitudes Survey, focusing on socio-economic conditions, study level, demographic backgrounds, work performance, online activity, and lifestyles within the UK. The analysis utilizes descriptive and inferential statistics, employing ...Read More

Running head: QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Quantitative Data Analysis Assignments
Name of the Student:
Name of the University:
Author’s Note:

1QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Table of Contents
Introduction:...............................................................................................................................2
Data Analysis:............................................................................................................................2
Descriptive Statistics:.............................................................................................................2
Box-plot:................................................................................................................................3
Paired two-sample t-test:........................................................................................................5
Independent sample t-test:......................................................................................................7
Parametric:...........................................................................................................................10
Pearson’s correlation coefficient:.....................................................................................10
Non-Parametric:...................................................................................................................10
Chi-square test:.................................................................................................................10
One-way ANOVA:...............................................................................................................12
MANOVA:...........................................................................................................................14
Multiple Regression Model:.................................................................................................18
Conclusion and Limitations:....................................................................................................22
Reference:................................................................................................................................23

2QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Table of Tables
Table 1: Table of descriptive statistics.......................................................................................3
Table 2: Tables of paired two-sample t-test...............................................................................6
Table 3: Table of independent sample t-test..............................................................................8
Table 4: Table of Pearson’s correlation coefficient.................................................................11
Table 5: The One-way ANOVA table.....................................................................................13
Table 6: The table of multiple comparisons.............................................................................14
Table 7: Table of Homogeneous subsets.................................................................................15
Table 8: Table of descriptive analysis of MANOVA analysis................................................16
Table 9: Fixed and random effect of multivariate tests of MANOVA analysis......................16
Table 10: Table of testing between-subject effects..................................................................16
Table 11: Table of comparison of Person’s age last birthday with respect to Person 1 sex for
“Males”....................................................................................................................................18
Table 12: Table of Multivariate test of homogeneity...............................................................18
Table 13: Table of Univariate Tests.........................................................................................18
Table 14: Table of Multiple R-square......................................................................................19
Table 15: ANOVA table of multiple regression model...........................................................20
Table 16: Table of intercept and slopes of multiple regression model....................................20
Table of Figures
Figure 1: Distribution of the variable “Respondent’s Socio-Economic Group (pre-SOC2000)
best estimate”.............................................................................................................................5
Figure 2: Distribution of the variable “Respondent’s Social Class (pre-SOC2000) best
estimate”.....................................................................................................................................5

3QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Figure 3: Distribution of the variable “Respondent’s Occupational Class (7 categories)”........6
Figure 4: The distribution of “Respondent NS-SEC Socio-economic Class” at analytic class
level............................................................................................................................................6
Figure 5: The grouped bar plot of selected two variables........................................................14
Figure 6: The histogram plot of residual values of the multiple regression model..................23
Figure 7: The normal probability plot of standardized residual of multiple regression model23

4QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Introduction:
The data analysis in this report and quantitative research highlights many surveyed
factors and effects of United Kingdom. Socio-economic conditions, study level, demographic
background, performance towards work, online activity, life styles and many more aspects of
life are present in the data set.
Focusing mainly descriptive statistics and inferential statistics, the researcher analysed
the data with the help of SPSS-20 software. The analysis would help to find out and highlight
the equality and diversity in mentality and behaviours among the people of countries of UK.
Data Analysis:
Descriptive Statistics:
Table 1: Table of descriptive statistics
Descriptive Statistics
N Range Minimum Maximum Mean Std.
Deviation
Variance
Respondent's Socio-
Economic Group
(pre-SOC2000) best
estimate
4134 18.00 2.00 20.00 8.9485 3.70671 13.740
Respondent: Social
class (pre-
SOC2000) best
estimate dv
4134 7.00 1.00 8.00 3.2121 1.39950 1.959
Respondent's
occupational class
(7 categories) dv
4184 7.00 1.00 8.00 3.7990 2.06574 4.267
Respondent NS-
SEC Socio-
economic Class
(analytic class
level): dv
4311 6.90 1.10 8.00 3.9452 2.12574 4.519
The descriptive statistics of the selected four variables displays that-
 Out of 4134 samples, the values of the best estimate of socio-economic group (pre-
SOC2000) varies in the interval of 2 to 20. The average and standard deviation of
these values are 8.9485 and 3.70671 respectively (Altman and Bland 1996).

5QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
 Out of chosen 4134 samples, the values of the best estimate of social class of
respondents varies in the interval of 1 to 8 with range 7. The mean and standard
deviation of these values are 3.2121 and 1.39950.
 Respondent’s occupational class for 4184 samples displays that the highest and lowest
values are 1 and 8 respectively with range 7. The average and standard deviation of
the values of these variables are respectively 3.7990 and 2.06574.
 Respondent NS-SEC Socio-economic class for 4311 samples indicates that the
highest and lowest values are respectively 1.1 and 8. The mean value and standard
deviation of the variable is calculated as 3.9452 and 2.12574.
Box-plot:
Figure 1: Distribution of the variable “Respondent’s Socio-Economic Group (pre-SOC2000) best estimate”
Most of values of the variable (75%) lie in the range of 12 to 7 (Wonnacott and Wonnacott
1990). The median value of the samples is 9. The outliers are the values equal to 20. The
outliers are 716, 900, 897 and 1013th samples (George and Mallery 2016).
Figure 2: Distribution of the variable “Respondent’s Social Class (pre-SOC2000) best estimate”

6QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Most of values of the variable (75%) lie in the range of 2 to 4. Median is calculated as 3. The
outliers are the values equal to 8. The outliers are 716, 900, 897 and 1013th samples.
Figure 3: Distribution of the variable “Respondent’s Occupational Class (7 categories)”
Most of the values of the variable (75%) lie in the interval of 2 to 6. The median value is
calculated as 3. No outlier is observed in the distribution of the undertaken variable.
Figure 4: The distribution of “Respondent NS-SEC Socio-economic Class” at analytic class level.

7QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Most of the values of the variable (75%) lie in the interval of 2 to 6. The median value is
calculated as 4. No outlier is observed in the distribution of the chosen variable.
Paired two-sample t-test:
Hypothesis:
Null hypothesis (H0): The average values of two variables “Which news website do you visit
more often” and “Which news website do you visit next more often” are equal to each other.
Alternative hypothesis (HA): The difference of average values of two variables “Which news
website do you visit more often” and “Which news website do you visit more often” is not
equal to 0.
Table 2: Tables of paired two-sample t-test

8QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
The average value of the first variable “Which news website do you visit most often”
is 15.01 for 2268 samples. The average value of the second variable “Which news website do
you visit next most often” is 15.16 for 2268 samples.
 Test applied: Paired two-sample t-test.
 Correlation coefficient: 0.49 with significant p-value 0.019.
 Level of significance: 0.05.
 Degrees of freedom: 2267
 Calculated t-statistic: (-0.172)
 Significant p-value: 0.864.
 Inference: The significant p-value 0.0864 is greater than 0.05. Therefore, the null
hypothesis is not rejected (Traitler Coleman and Burbidge 2017).

9QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
 Interpretation: As the null hypothesis is failed to reject, therefore, it could be
interpreted that the average values of two variables “Which news website do you visit
most often?” and “Which news website do you visit next most often?” are unequal.
 Decision-making: According to the average, the two variables are almost equal to
each other. Therefore, no change would occur significantly in future days in case of
visiting news website (De Winter 2013).
Independent sample t-test:
Null hypothesis (H0): The average values of dependent variable “Which forms of transport
do you think contribute most to climate change: cars: Versions B, C, D” for number of trips 0
or 1 are equal.
Alternative hypothesis (HA): The average values of dependent variable “Which forms of
transport do you think contribute most to climate change: cars: Versions B, C, D” for number
of trips 0 or 1 are unequal.
Table 3: Table of independent sample t-test
Group Statistics
How many trips did you
make by plane during the
last 12 months?: Versions
B, C, D
N Mean Std.
Deviation
Std. Error
Mean
Which forms of
transport do you think
contribute most to
climate change: cars:
Versions B, C, D
0 1639 .78 1.202 .030
1 616 .82 1.096 .044
Which forms of
transport do you think
contribute most to
climate change: buses:
Versions B, C, D
0 1639 .69 1.221 .030
1 616 .63 1.134 .046
Which forms of
transport do you think
contribute most to
climate change: vans:
Versions B, C, D
0 1639 .93 1.159 .029
1 616 .91 1.064 .043
Which forms of
transport do you think
contribute most to
climate change:
planes: Versions B, C,
D
0 1639 .67 1.223 .030
1 616 .68 1.128 .045
Which forms of 0 1639 .21 1.201 .030

10QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
transport do you think
contribute most to
climate change: trains:
Versions B, C, D
1 616 .20 1.101 .044
Which forms of
transport do you think
contribute most to
climate change: ships:
Versions B, C, D
0 1639 .24 1.207 .030
1 616 .24 1.111 .045
Which forms of
transport do you think
contribute most to
climate change:
motorbikes: Versions
B, C, D
0 1639 .25 1.210 .030
1 616 .21 1.106 .045
Which forms of
transport do you think
contribute most to
climate change: none
of these: Versions B,
C, D
0 1639 .17 1.191 .029
1 616 .14 1.082 .044
Which forms of
transport do you think
contribute most to
climate change: don't
believe/happen
anyway: Versions B,
C, D
0 1639 .17 1.191 .029
1 616 .14 1.084 .044

11QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
(Panik 2012)
 Test applied: One variable independent sample t-test.
 Level of significance: 5%.
 Degrees of freedom: 2253 (when equal variances are assumed) and 1207 (when
unequal variances are assumed).
For all the variables with respect to the factor variable “How many trips did you make by
plane during the last 12 months?: Versions B, C, D”, the significant p-values are greater than
5% (level of significance). Hence, all the variables with respect to mediator variable, have
equal averages in case of no trip and at least one trip (Abbott 2017). The means of various
observations of “Which forms of transport do you think contribute most to climate change:
don't believe/happen anyway: Versions B, C, D” with respect to number of yearly trips (0 or
1) are equal to each other.

12QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Parametric:
Pearson’s correlation coefficient:
Table 4: Table of Pearson’s correlation coefficient
The Pearson’s correlation coefficient between two scale variables are calculated here. These
are - “Urban/Rural Indicator 2011 (England and Wales)” and “Urban/Rural Indicator 2011
(Scotland)”.
Test statistic: (-0.719).
Significant p-value: 0.0.
Interpretation: As r = (-0.719), therefore, it could be interpreted that the correlation is strong
and negative (Mukaka 2012).
Conclusion: The value of correlation coefficient is negative and statistically significant.
Therefore, it could be interpreted that if the urban or rural indicator of England and Wales
increases, then urban or rural indicator of Scotland significantly decreases and vice-versa.
Non-Parametric:
Chi-square test:
Null hypothesis (H0): The two variables “Do you have internet access at
home/work/elsewhere or on smartphone/tablet/mobile device” and “Do you have a personal
Twitter account?” are independent to each other. That is, there exists no association between
these two variables.

13QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Alternative hypothesis (HA): The two variables “Do you have internet access at
home/work/elsewhere or on smartphone/tablet/mobile device” and “Do you have a personal
Twitter account?” are associated with each other.
Chi-square test is applied to find the association between two categorical variables.
The interpretation may also tend to find the independence of two variables too.
Out of 3539 samples who have internet access, 790 people has twitter amount and
2749 people do not have twitter amount. Out of 89 samples who do not have internet access,
only 4 people has twitter amount and 785 people do not have twitter amount (Field 2013).
 Test applied: Chi-square t-test.
 Level of significance: 0.05.
 Degrees of freedom: 1

14QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
 Calculated Chi-square statistic: 204.973.
 Significant p-value: 0.0.
 Inference: The significant p-value 0.0 is lesser than 0.05. Therefore, the null
hypothesis is rejected at 5% level of significant.
 Interpretation: As the null hypothesis is rejected, therefore, the alternative
hypothesis is not rejected. It could be interpreted that the two variables “Do you
personally have internet access at home or other places on mobile or other gadgets?”
and “Do you have a personal twitter account?” are associated with each other.
 Decision-making: These two variables are significantly associated with each other.
Figure 5: The grouped bar plot of selected two variables
One-way ANOVA:
Null hypothesis (H0): The means of expected retired ages from main job in all the three
countries alike England, Scotland and Wales are equal.
Alternative hypothesis (HA): There exists at least one inequality in the means of expected
retired ages from main job in all the three countries alike England, Scotland and Wales.
One-way ANOVA (analysis of variance) test examines the equality averages of the
chosen variables within a certain statistical significant level (Leech, Barrett and Morgan
2013).
Table 5: The One-way ANOVA table

15QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
The values of the variable “At what age do you expect to retire from your main job?” are
separated according to the three countries that are “England”, “Scotland” and “Wales”. The
average estimated age of retirement for all the three countries are 66.88 years, 68.27 years
and 67.22 years respectively.
(Norusis 2008.)
 Test applied: One-way ANOVA test.
 Level of significance: 0.05.
 Degrees of freedom: 1208
 Calculated F-statistic: 0.884.
 Significant p-value: 0.413.
 Inference: The significant p-value 0.413 is lesser than 0.05. Therefore, the null
hypothesis is not rejected at 5% level of significant.
 Interpretation: The null hypothesis is accepted with 5% level of significance. It
could be interpreted that the average ages of expectation of retirement in “England”,
“Scotland” and “Wales” are equal to each other with 95% probability.
 Decision-making: As the mean expected ages of the responders from “England”,
“Scotland” and “Wales” are same, therefore, it could be concluded that the peoples of
all the three counties regard the same consideration about the age of retirement.
Post Hoc Tests
Table 6: The table of multiple comparisons

16QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Table 7: Table of Homogeneous subsets
The significant p-value of the expected ages of retirement responded from chosen three
counties found to be 0.530. Hence, these average responses are equal to each other.
MANOVA:
One-way multivariate analysis (One-way MANOVA) determines whether there are
any differences between independent groups on at least two continuous dependent variables.
Actually, one-way MANOVA is an omnibus test statistic and fails to refer which specific
groups were significantly different from each other (Montgomery, Runger and Hubele 2009).
Null hypothesis (H0): The means of ages of the persons in all the nine observations are equal
when phone 1 sex relation is assumed male.
Alternative hypothesis (HA): There exists at least one inequality in the means of ages of the
persons in all the nine observations when phone 1 sex relation is assumed male.

17QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Table 8: Table of descriptive analysis of MANOVA analysis
Table 9: Fixed and random effect of multivariate tests of MANOVA analysis
The calculated F (2, 1) = 27.672. Here, p-value is 0.133 which is greater than 0.05.
Wilk’s ᴧ = 0.018, partial ղ2 = 0.982.
Therefore, there is statistically significant difference in ages of males based on observations
of males (Van Aelst and Willems 2011).
Table 10: Table of testing between-subject effects

18QUANTITATIVE DATA ANALYSIS ASSIGNMENTS

19QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
It could be observed that p-value of observed F-statistics is 0.0. As p-value < 0.05, therefore,
the presence of statistical significance is accepted at 5% level of significance.
Estimated Marginal Means
Table 11: Table of comparison of Person’s age last birthday with respect to Person 1 sex for “Males”
Estimates
Dependent Variable Person 1 sex Mean Std. Error 95% Confidence Interval
Lower Bound Upper Bound
Person 1 age last
birthday Male 25.333 7.333 -6.219 56.886
Person 2 age last
birthday Male 55.000 10.149 11.333 98.667
Person 3 age last
birthday Male 52.667 11.348 3.840 101.493
Person 4 age last
birthday Male 28.000 6.928 -1.810 57.810
Person 5 age last
birthday Male 26.333 7.796 -7.210 59.877
Person 6 age last
birthday Male 23.667 6.438 -4.033 51.366
Person 7 age last
birthday Male 13.000 2.517 2.172 23.828
Person 8 age last
birthday Male 10.000 2.000 1.395 18.605
Person 9 age last
birthday Male 4.000 1.000 -.303 8.303
Table 12: Table of Multivariate test of homogeneity
Multivariate Tests
Value F Hypothesis
df
Error dfSig. Partial Eta
Squared
Noncent.
Parameter
Observed
Powera
Pillai's trace .000 . .000 .000 . . . .
Wilks'
lambda 1.000 . .000 1.500 . . . .
Hotelling's
trace .000 . .000 2.000 . . . .
Roy's largest
root .000 .000 2.000 .000 . .000 .000 .
Each F tests the multivariate effect of Person 1 sex. These tests are based on the linearly
independent pairwise comparisons among the estimated marginal means.
a. Computed using alpha = .05

20QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Table 13: Table of Univariate Tests
(Leech, Barrett and Morgan 2013)
Multiple Regression Model:
The multiple regression model refers the linear statistical significance between
dependent variable and independent variables. Here, the response variable is “Importance of
job involving personal contacts with others: Versions B, D”. The dependent variables are-
How important in a job: deciding own times or days of work (observed in 8 periods).
Null hypothesis (H0): There exists any statistically significant linear association between the
variables “Importance of job involving personal contact with others” and the eight different
observations of “How important in a job”.
Alternative hypothesis (HA): There does not exist a statistically significant linear association
between the variables “Importance of job involving personal contact with others” and the
eight different observations of “How important in a job”.
Table 14: Table of Multiple R-square

21QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
The value of multiple R2 in multiple regression model is 0.637. It is also known as the
“coefficient of variation” (Konasani and Kadre 2015). Therefore, the predictor variables can
explain 63.7% variability of the response variable.
Table 15: ANOVA table of multiple regression model
The ANOVA regression model displays that the value of F-statistic is 390.768. The
significant p-value is calculated as 0.0. The calculated p-value is less than 5% level of
significance. Therefore, the null hypothesis of linear significant association between
dependent variable and independent variables is accepted (Data and Bartz 1988).
Table 16: Table of intercept and slopes of multiple regression model

22QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Coefficientsa
Model Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
B Std. Error Beta
1
(Constant) .351 .049 7.115 .000
How important in a job:
job security: Versions
B, D
.052 .023 .050 2.328 .020
How important in a job:
high income: Versions
B, D
-.042 .025 -.042 -1.706 .088
How important in a job:
good opportunities for
advancement: Versions
B, D
.017 .025 .018 .688 .491
How important in a job:
an interesting job:
Versions B, D
.230 .025 .218 9.129 .000
How important in a job:
working independently:
Versions B, D
.046 .024 .048 1.897 .058
How important in a job:
helping other people:
Versions B, D
.237 .027 .241 8.931 .000
How important in a job:
useful to society:
Versions B, D
.205 .024 .213 8.539 .000
How important in a job:
deciding own times or
days of work: Versions
B, D
.166 .021 .171 7.829 .000
a. Dependent Variable: Importance of job involving personal contact with others: Versions B,
D
The multiple regression model is calculated as-
“Importance of job involving personal contacts with others: Versions B, D” = 0.351 +
∑ β i∗(How important in a job: job security: Versions B, D)i .
The p-values of are less than 0.05 for the 4th, 6th, 7th and 8th observation of “Importance of job
involving personal contacts with others: Versions B, D”. Hence, these observations of the
predictor variables are statistically and significantly related to the response variable. The
significant variables are “job security”, “an interesting job”, “helping other people”, “useful
to society” and “deciding own times or days of work”. The insignificant factors of the model
are “high income”, “good opportunities for advancement” and “working independently”. All
the predictors except “high income” is positively associated with the dependent variable.
Therefore, it the values of predictors (except “high income”) increase, the value of response
also increases and vice versa (Brandt 2014).

23QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Figure 6: The histogram plot of residual values of the multiple regression model
The residual plot as a histogram indicates that the residuals a normally distributed.
Figure 7: The normal probability plot of standardized residual of multiple regression model
The normal probability plot displays that the fitting is not bad.

24QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Conclusion and Limitations:
The analysis displays that the economic conditions of the households of UK
inhabitants are overall prospered (Lindley 1996). They informed that their TV news channels
are enough satisfactory. Therefore, they would like to continue watching the similar TV
channels in near future. The internet facility is available is available to most of the inhabitants
and a significant number of the inhabitants have thereby Twitter account. The males among
the sampled people equally prefer bus, cars and all other vehicles as the modes of
transportation at the time of tour. Note that, the numbers of tours are very lower in count such
as either once in a year or never in a year.
Surprisingly the significant negative correlation indicates that urban or rural
development indexes for the “Scotland” and “England & Wales” are against to each other.
However, the expected mean age of retirement from permanent job according to all the three
provinces are almost same. Age levels according to the last birthday of the male candidates
are unequal to each other. In those sampled data, the significant association among
importance of job in case of communication and different types of factors such as high
income, job security and other factors are found.
The all data is not utilized in this short report. It is one of the major drawback. Not
only that, the present of missing data and secondary responses may cause bias in the data set
as well as data analysis. The number of parameters of this big data is high. Therefore, the data
is not easy to handle and the analysis is not easy to carry out.

25QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Reference:
Abbott, M.L., 2017. Independent Sample T Test.
Altman, D.G. and Bland, J.M., 1996. Detecting skewness from summary information. British
Medical Journal, 313(7066), pp.1200-1201.
Brandt, S., 2014. Testing Statistical Hypotheses. In Data Analysis (pp. 175-207). Springer,
Cham.
Data, S. and Using Descriptive Statistics Bartz, A.E., 1988. Basic statistical concepts. New
York: Macmillan. Devore, J., and Peck.
De Winter, J.C., 2013. Using the Student's t-test with extremely small sample sizes. Practical
Assessment, Research & Evaluation, 18(10).
Field, A., 2013. Discovering statistics using IBM SPSS statistics. sage.
George, D. and Mallery, P., 2016. IBM SPSS Statistics 23 step by step: A simple guide and
reference. Routledge.
Konasani, V.R. and Kadre, S., 2015. Multiple regression analysis. In Practical Business
Analytics Using SAS (pp. 351-399). Apress, Berkeley, CA.
Leech, N., Barrett, K. and Morgan, G.A., 2013. SPSS for intermediate statistics: Use and
interpretation. Routledge.
Lindley, R.M., 1996. The school-to-work transition in the United Kingdom. Int'l Lab.
Rev., 135, p.159.
Montgomery, D.C., Runger, G.C. and Hubele, N.F., 2009. Engineering statistics. John Wiley
& Sons.
Mukaka, M.M., 2012. A guide to appropriate use of correlation coefficient in medical
research. Malawi Medical Journal, 24(3), pp.69-71.
Norusis, M., 2008. SPSS Statistics 17.0: Guide to data analysis. Prentice-Hall.
Panik, M.J., 2012. Testing Statistical Hypotheses. Statistical Inference: A Short Course,
pp.184-216.
Traitler, H., Coleman, B. and Burbidge, A., 2017. Testing the hypotheses. Food Industry
R&D: A New Approach, pp.227-247.
Van Aelst, S. and Willems, G., 2011. Robust and efficient one-way MANOVA tests. Journal
of the American Statistical Association, 106(494), pp.706-718.

26QUANTITATIVE DATA ANALYSIS ASSIGNMENTS
Wonnacott, T.H. and Wonnacott, R.J., 1990. Introductory statistics (Vol. 5). New York:
Wiley.