GENG4402: Analysis of First Order Control Systems - Pre-Lab 1
VerifiedAdded on 2022/10/11
|5
|910
|97
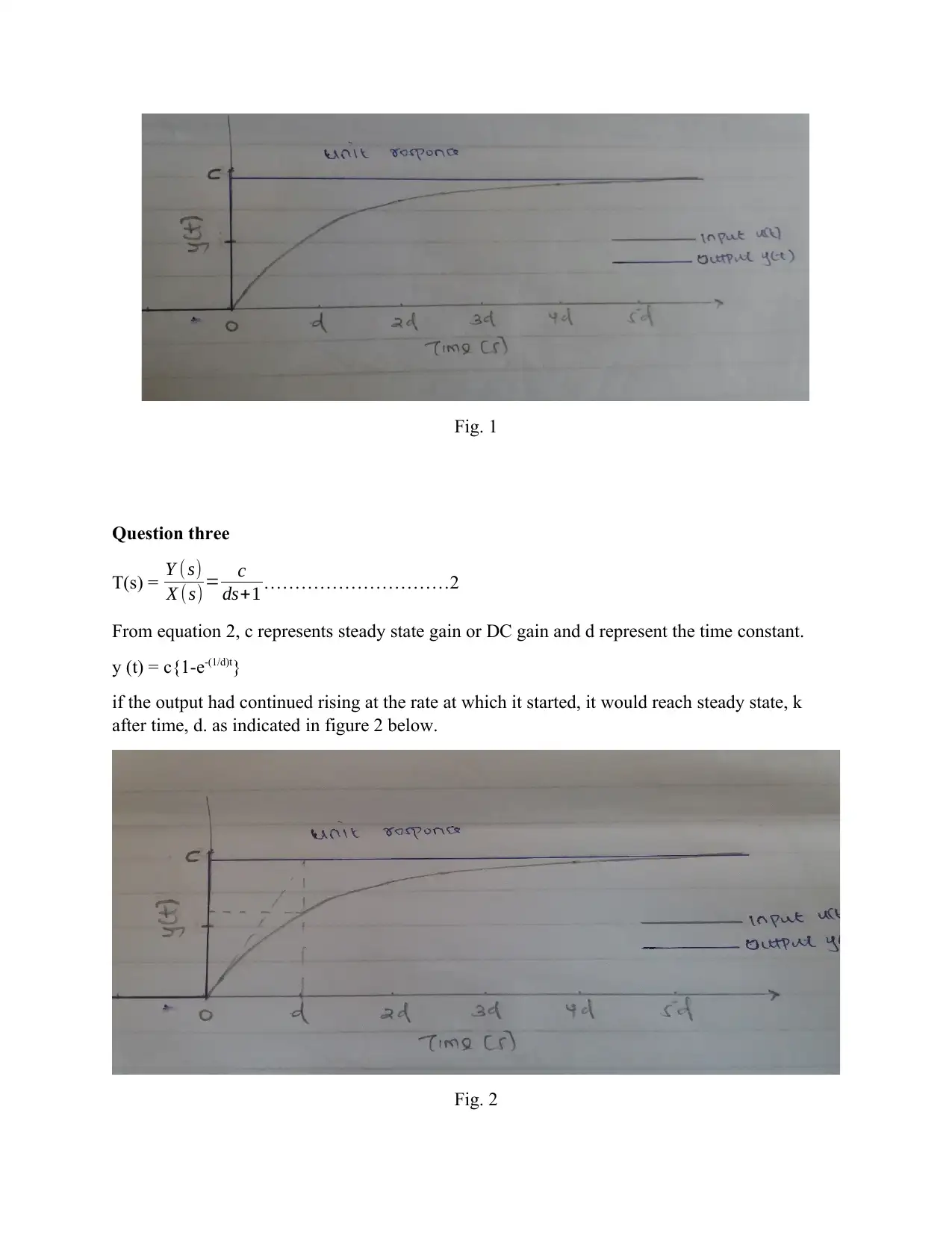
Homework Assignment
AI Summary
This document presents a comprehensive solution to a pre-lab assignment on first-order control systems (GENG4402). The solution begins by explaining the significance of the transfer function representation in analyzing the system's behavior, including its order, frequency response, and stability. It then derives the output response to a unit step input, providing detailed calculations using Laplace transforms and partial fraction decomposition, and plots the input and output signals. The analysis continues by determining the steady-state gain and time constant from the plots. The solution establishes the relationship between the parameters of the transfer function (c and d) and the coefficients of the time-domain equation (a and b). Finally, it explores the impact of increasing the parameter 'b' on the system's stability. References to relevant control systems literature are also included.
1 out of 5










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)