Analysis of R&D Expenses and Assets in Firms

This article analyzes the relationship between R&D expenses and assets in firms using scatter plots, regression models, and histograms. It also discusses the impact of cost of goods sold and total assets on R&D spending.

Business Statistics
1

Q1.R& D Expenses
Q2.
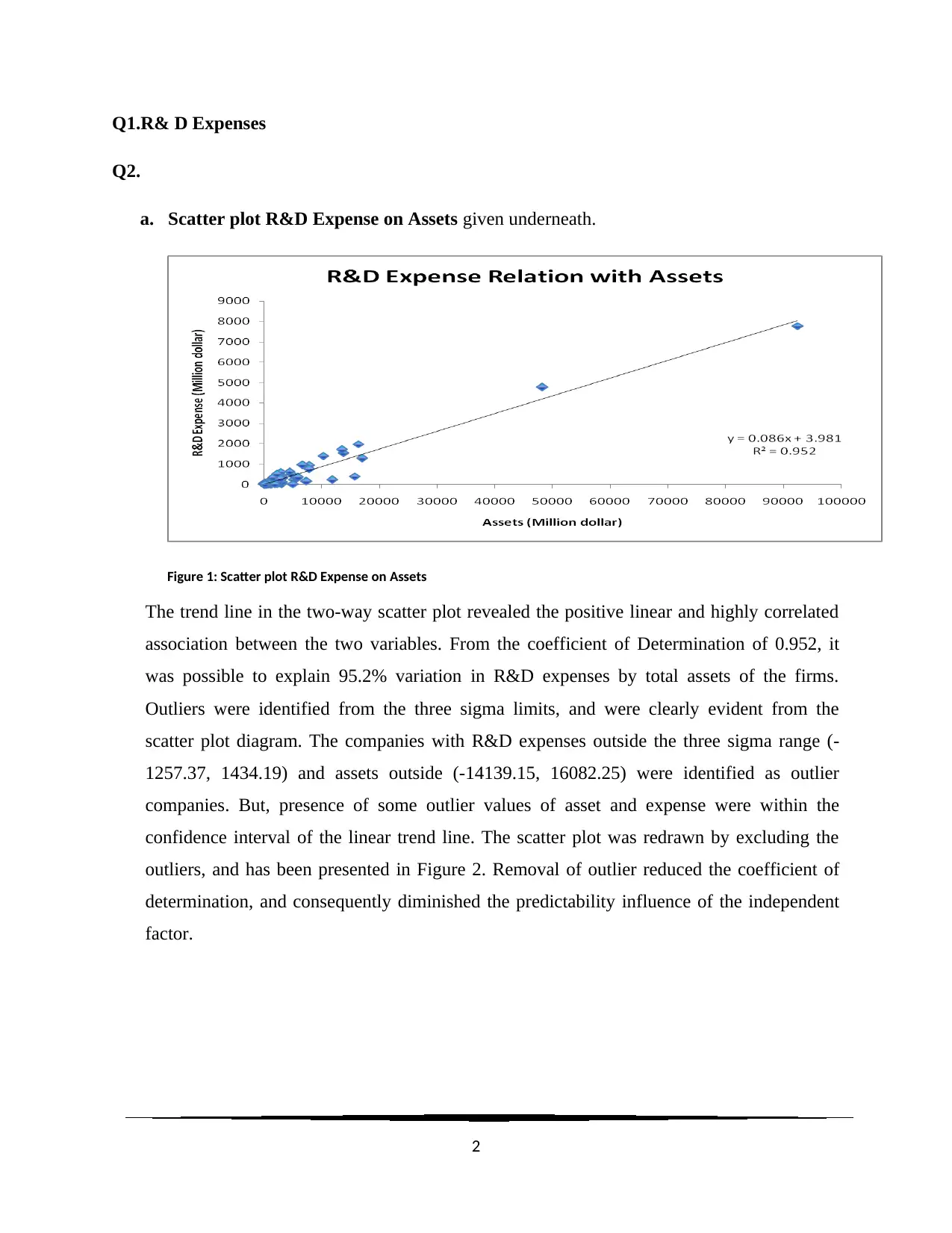
a. Scatter plot R&D Expense on Assets given underneath.
Figure 1: Scatter plot R&D Expense on Assets
The trend line in the two-way scatter plot revealed the positive linear and highly correlated
association between the two variables. From the coefficient of Determination of 0.952, it
was possible to explain 95.2% variation in R&D expenses by total assets of the firms.
Outliers were identified from the three sigma limits, and were clearly evident from the
scatter plot diagram. The companies with R&D expenses outside the three sigma range (-
1257.37, 1434.19) and assets outside (-14139.15, 16082.25) were identified as outlier
companies. But, presence of some outlier values of asset and expense were within the
confidence interval of the linear trend line. The scatter plot was redrawn by excluding the
outliers, and has been presented in Figure 2. Removal of outlier reduced the coefficient of
determination, and consequently diminished the predictability influence of the independent
factor.
2

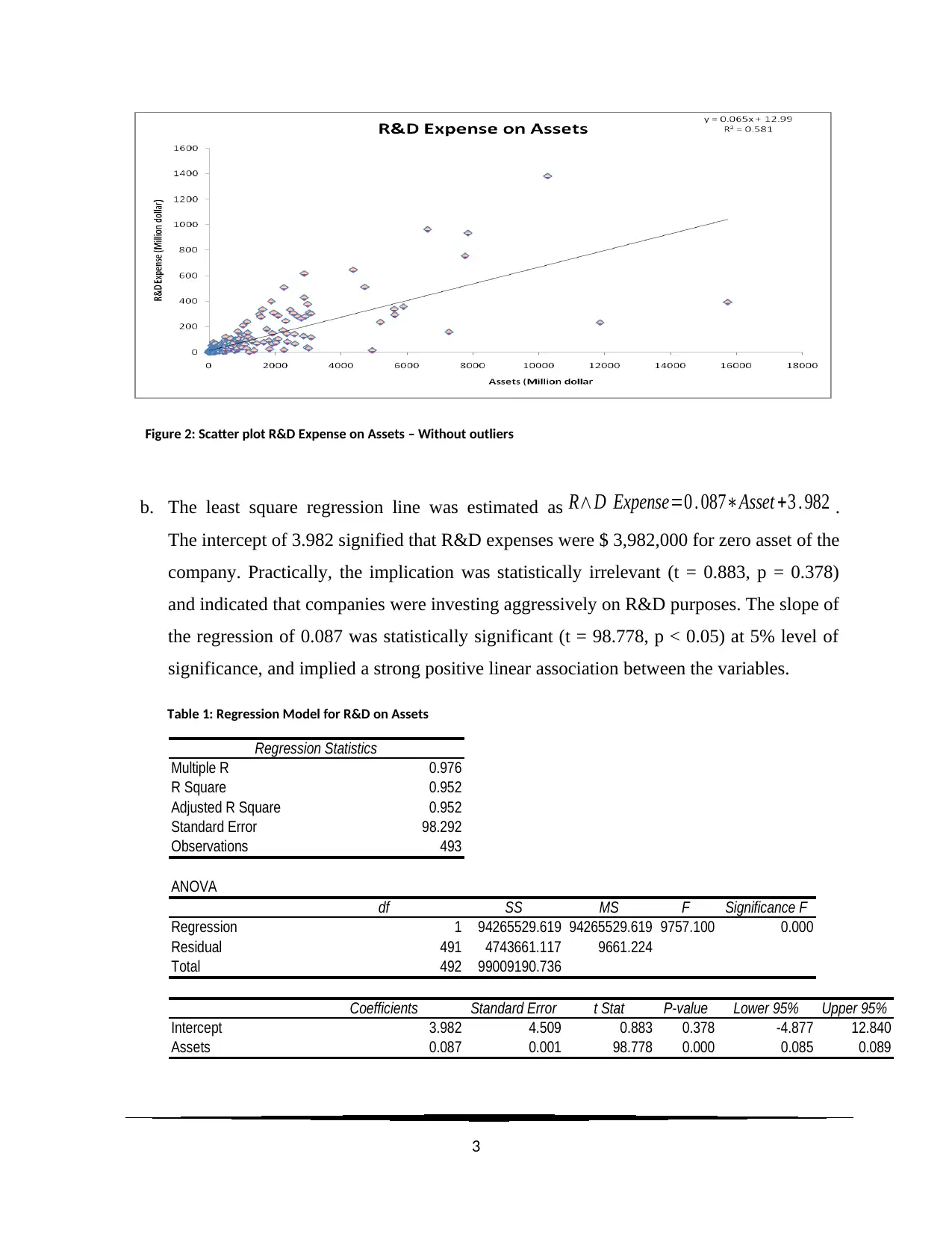
Figure 2: Scatter plot R&D Expense on Assets – Without outliers
b. The least square regression line was estimated as R∧D Expense=0 . 087∗Asset +3 . 982 .
The intercept of 3.982 signified that R&D expenses were $ 3,982,000 for zero asset of the
company. Practically, the implication was statistically irrelevant (t = 0.883, p = 0.378)
and indicated that companies were investing aggressively on R&D purposes. The slope of
the regression of 0.087 was statistically significant (t = 98.778, p < 0.05) at 5% level of
significance, and implied a strong positive linear association between the variables.
Table 1: Regression Model for R&D on Assets
Regression Statistics
Multiple R 0.976
R Square 0.952
Adjusted R Square 0.952
Standard Error 98.292
Observations 493
ANOVA
df SS MS F Significance F
Regression 1 94265529.619 94265529.619 9757.100 0.000
Residual 491 4743661.117 9661.224
Total 492 99009190.736
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 3.982 4.509 0.883 0.378 -4.877 12.840
Assets 0.087 0.001 98.778 0.000 0.085 0.089
3

c. Coefficient of determination was 0.952, implying 95.2% variation in R&D expenses were
explained by total assets of the company. In fact, the adjusted R square for the inclusion of
Assets as an impact factor implied the statistical significance of the predictor (t = 98.78, p <
0.05). The standard error of 0.001 or 0.1% signified that the observations were within the
0.1% spread ($ -166940.16, $ 173716.20) of the regression equation. The regression line
accurately characterized the strong positive correlation between the variables.
d. The histograms of both the variables were highly right skewed, indicating presence of high
R&D expense, asset values for the companies. The scatter plot also indicated the same trend
of the data, and here also the similar trend was observed.
Figure 3: Histogram of Expense on R&D
Figure 4: Histogram of Assets
4

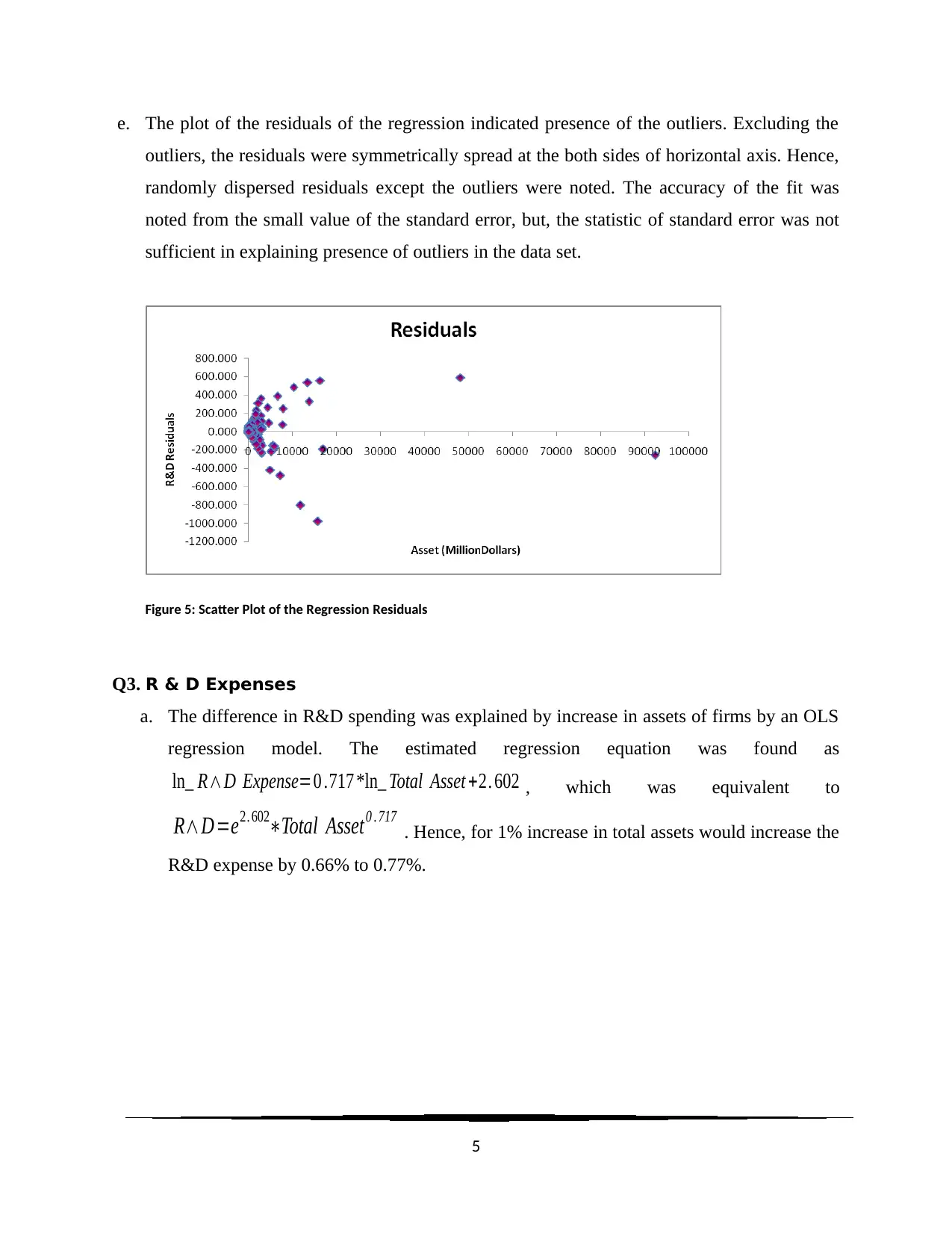
e. The plot of the residuals of the regression indicated presence of the outliers. Excluding the
outliers, the residuals were symmetrically spread at the both sides of horizontal axis. Hence,
randomly dispersed residuals except the outliers were noted. The accuracy of the fit was
noted from the small value of the standard error, but, the statistic of standard error was not
sufficient in explaining presence of outliers in the data set.
Figure 5: Scatter Plot of the Regression Residuals
Q3. R & D Expenses
a. The difference in R&D spending was explained by increase in assets of firms by an OLS
regression model. The estimated regression equation was found as
ln_ R∧D Expense=0 .717 *ln_ Total Asset +2. 602 , which was equivalent to
R∧D=e2. 602∗Total Asset0 . 717
. Hence, for 1% increase in total assets would increase the
R&D expense by 0.66% to 0.77%.
5

Table 2: Regression Model for ln_R&D on ln_Assets
ln_Expense: R&D ln_Total Assets
Regression Statistics
Multiple R 0.837
R Square 0.700
Adjusted R Square 0.699
Standard Error 1.242
Observations 323
ANOVA
df SS MS F Significance F
Regression 1 1157.132 1157.132 750.175 0.000
Residual 321 495.137 1.542
Total 322 1652.269
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.602 0.504 5.160 0.000 1.610 3.594
ln_Total Assets 0.717 0.026 27.389 0.000 0.665 0.768
b. The regression model with log base 10 was constructed and has been provided below.
Table 3: Regression Model for log_R&D on log_Assets
log_Expense: R&D log_Total Assets
Regression Statistics
Multiple R 0.837 26.23810598
R Square 0.700 29.08356569
Adjusted R Square 0.699
Standard Error 0.539
Observations 323
ANOVA
df SS MS F Significance F
Regression 1 218.249 218.249 750.175 0.000
Residual 321 93.389 0.291
Total 322 311.637
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.130 0.219 5.160 0.000 0.699 1.561
log_Total Assets 0.717 0.026 27.389 0.000 0.665 0.768
The estimated regression was found to be similar with the regression equation with
natural logarithm base of the variables.
6

c. The 95% prediction interval for the R&D expenses as $ 1 billion in assets was calculated
as X ±1. 96∗σ =[−$ 39 , 92 , 63 , 961. 50 , $ 2 , 39 ,92 , 63 , 961. 50 ] where σ =$ 713910184 . 44 was the
standard deviation of R&D expenses. The 95% confidence interval was estimated as
[$ 8, 06, 33,489.70, $ 23, 63, 47, 748.69], and noted that the prediction interval contained
the confidence interval of average R&D of the population. As, the 95% prediction
interval included the 95% confidence interval for average R&D expenses, it was expected
to have 95% coverage of the data set.
R & D Expenses problem
a. The scatter plots for the log of spending on R&D versus the log of total assets, and the
log of the cost of goods sold have been provided below.
Figure 6: Log of spending on R&D versus the log of total assets
7

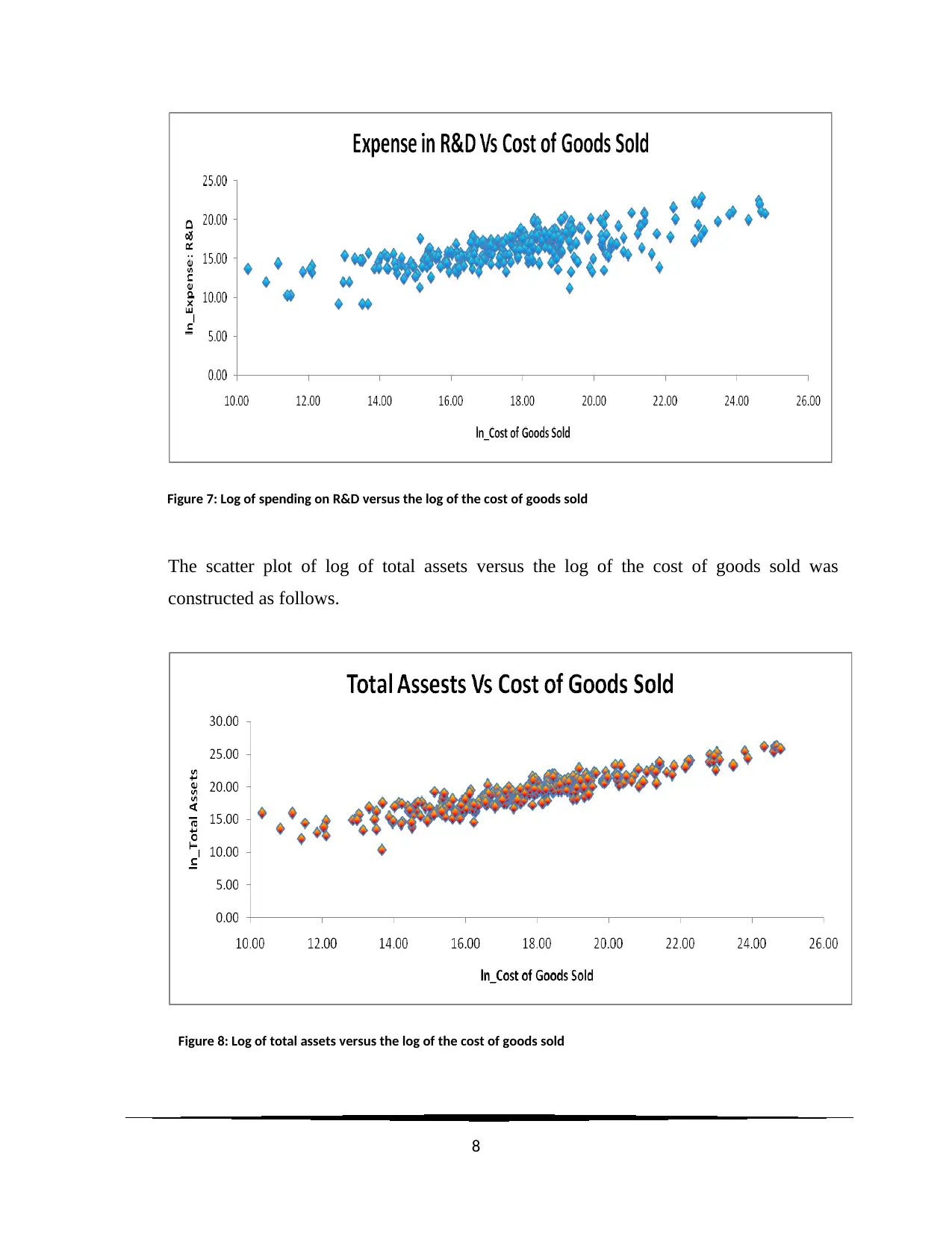
Figure 7: Log of spending on R&D versus the log of the cost of goods sold
The scatter plot of log of total assets versus the log of the cost of goods sold was
constructed as follows.
Figure 8: Log of total assets versus the log of the cost of goods sold
8

The high positive correlation of predictors with the dependent variable was desired for linear
regression model. But, the cost of goods sold and total assets have high positive correlation,
and this could generate problem of multi-co-linearity. Effect of one of the predictors could
be suppressed by another predictor. Hence, Multiple Regression with log of total assets, and
the log of the cost of goods sold would violate one of the assumptions of MRM.
b. The Multiple Regression model was constructed as below with cost of goods sold and total
assets as predictors to estimate R&D expenses with a logarithmic transformation to all the
variables.
Table 4: Multiple Regression Model with cost of goods sold and total assets
Regression Statistics
Multiple R 0.841
R Square 0.707
Adjusted R Square 0.705
Standard Error 1.234
Observations 320
ANOVA
df SS MS F Significance F
Regression 2 1164.253 582.126 382.357 0.000
Residual 317 482.622 1.522
Total 319 1646.875
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.703 0.505 5.351 0.000 1.709 3.697
ln_Total Assets 0.866 0.062 13.956 0.000 0.744 0.988
ln_Cost of Goods Sold -0.167 0.063 -2.635 0.009 -0.292 -0.042
The regression equation was found as
ln_ R∧D Expense=−0 .167 *ln_ Cost of Goods Sold +0 . 866 *ln_Total Assets+2. 703
All the variables were in natural logarithmic transformed scale. The model was found to be
statistically significant (F = 382.357, P < 0.05) where total assets (t = 13.96, p < 0.05) and
cost of goods sold (t = - 2.64, p < 0.05) were found to be significant predictors for the R&D
expenses. The predictors were able to explain 70.7% variation of R&D expenses and
inclusion of them reduced the adjusted R square to 70.5%. Overall a good fit was observed
with probable multi-co-linearity issue.
9

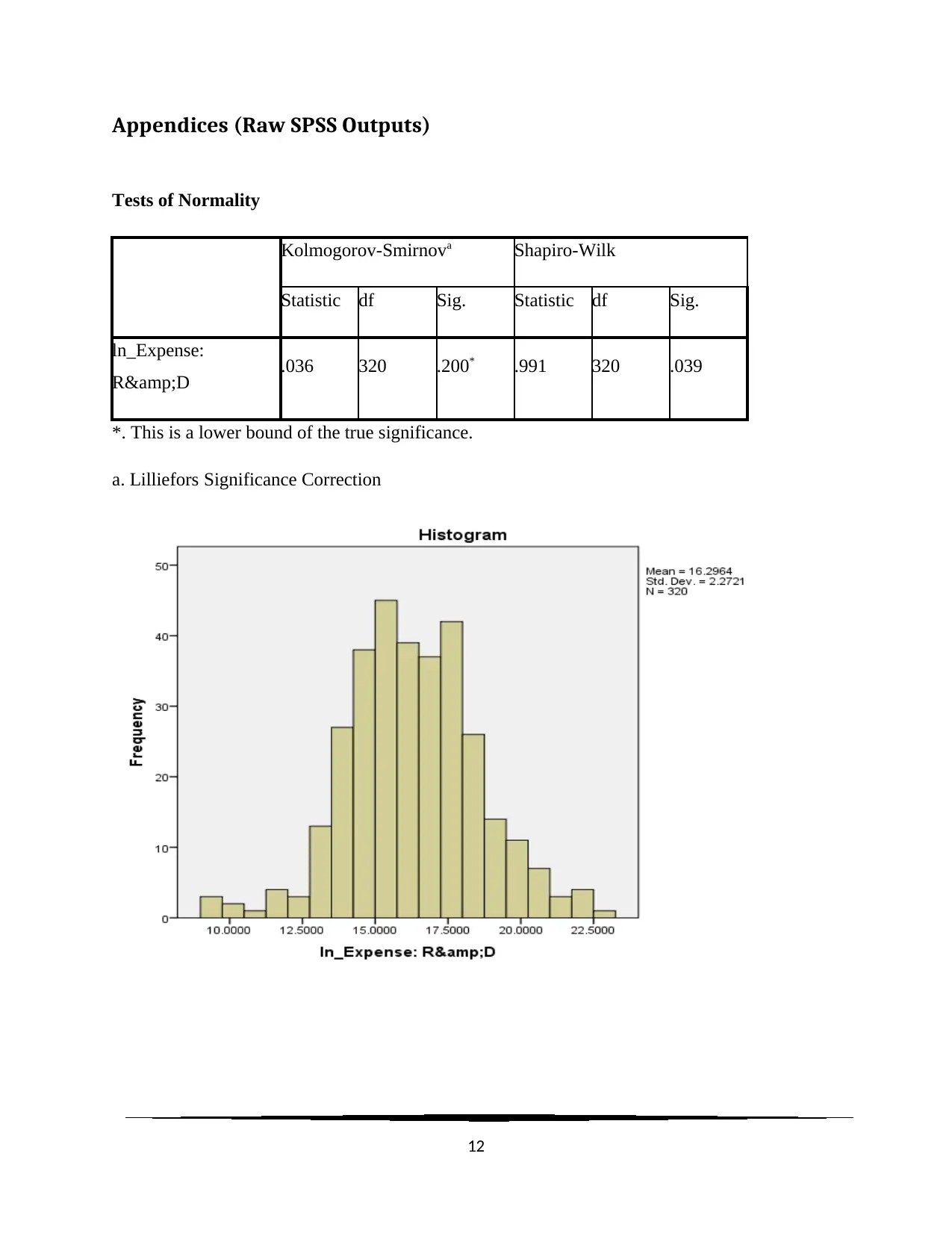
c. The ln_R&D expenses was found to be normally distributed with Shapiro-Wilk test (W
(320) = 0.991, P < 0.05) at 5% level of significance with existence of some outlier values.
Correlation between the dependent and predictor variables were positive and above 0.7,
indicating the accurate estimation possibility of the regression model. But, the high positive
correlation between the predictors generated multi-co-linearity issue in the model. The
difference in R square was noted to be – 0.28%. Hence, predictors were good estimator of
the dependent variable. Case wise diagnostics found that four observations had standard
residuals outside the three sigma limit, indicating problem of Homoscedasticity.
d. The MRM model with log of assets as the only predictor was constructed as below.
Table 5: Multiple Regression Model with total assets in log scale
Regression Statistics
Multiple R 0.841
R Square 0.707
Adjusted R Square 0.705
Standard Error 1.234
Observations 320
ANOVA
df SS MS F Significance F
Regression 2 1164.253 582.126 382.357 0.000
Residual 317 482.622 1.522
Total 319 1646.875
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.703 0.505 5.351 0.000 1.709 3.697
ln_Total Assets 0.866 0.062 13.956 0.000 0.744 0.988
ln_Cost of Goods Sold -0.167 0.063 -2.635 0.009 -0.292 -0.042
From the MRM model with log of assets alone it was noted that the previous model with
cost of goods sold and total assets as predictors to estimate R&D expenses with a
logarithmic transformation was equally statistically significant to the present model
(Gujarati, 2011).
e. The slope of the log of the cost of goods sold in the estimated regression equation was
-0.167, which indicated negative partial elasticity or inelasticity of R&D spending. The
confidence interval for partial elasticity of R&D spending with respect cost of goods sold
was [$ 1339212, $ 958509.2], specifying that with 95% confidence it was possible to assess
10

that partial elasticity of R&D spending with respect cost of goods sold was with the
specified range of the confidence interval.
f. Marginal utility of 0.60 for R&D spending with respect to CGS was absolutely okay. The
partial utility of R&D spending with respect to CGS was suppressed by the impact of total
assets. The multi-co-linearity problem was the reason for this suppression, and negative
impact of CGS on R&D spending. From the OLS regression of R&D spending with respect
to CGS yielded the marginal utility as 0.636 (Asteriou, & Hall, 2015).
Table 6: OLS Regression Model with cost of goods sold
Regression Statistics
Multiple R 0.726
R Square 0.527
Adjusted R Square 0.525
Standard Error 1.565
Observations 320
ANOVA
df SS MS F Significance F
Regression 1 867.713 867.713 354.141 0.000
Residual 318 779.162 2.450
Total 319 1646.875
Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0%
Intercept 5.037 0.605 8.331 0.000 3.848 6.227 3.848 6.227
ln_Cost of Goods Sold 0.636 0.034 18.819 0.000 0.570 0.703 0.570 0.703
References
Asteriou, D., & Hall, S. G. (2015). Applied econometrics. Macmillan International Higher
Education.
Gujarati, D. N. (2011). Econometrics by example. Palgrave Macmillan,.
11

Appendices (Raw SPSS Outputs)
Tests of Normality
Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
ln_Expense:
R&amp;D .036 320 .200* .991 320 .039
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
12

Correlations
ln_Expense:
R&amp;D
ln_Total
Assets
ln_Cost of
Goods Sold
Pearson Correlation
ln_Expense:
R&amp;D 1.000 .837 .726
ln_Total Assets .837 1.000 .907
ln_Cost of Goods
Sold .726 .907 1.000
Sig. (1-tailed)
ln_Expense:
R&amp;D . .000 .000
ln_Total Assets .000 . .000
ln_Cost of Goods
Sold .000 .000 .
N
ln_Expense:
R&amp;D 320 320 320
ln_Total Assets 320 320 320
ln_Cost of Goods
Sold 320 320 320
Model Summaryb
13

Model R R Square Adjusted R
Square
Std. Error
of the
Estimate
Change Statistics
R Square
Change
F Change df1df2 Sig. F
Change
1 .841a .707 .705 1.2338819 .707 382.357 2 317.000
a. Predictors: (Constant), ln_Cost of Goods Sold, ln_Total Assets
b. Dependent Variable: ln_Expense: R&amp;D
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 1164.250 2 582.125 382.357 .000b
Residual 482.621 317 1.522
Total 1646.872 319
a. Dependent Variable: ln_Expense: R&amp;D
b. Predictors: (Constant), ln_Cost of Goods Sold, ln_Total Assets
Coefficientsa
14

Model Unstandardized
Coefficients
Standardized
Coefficients
t Sig. Correlations
B Std. Error Beta Zero-
order
PartialPart
1
(Constant) 2.703 .505 5.351 .000
ln_Total Assets .866 .062 1.010 13.956.000.837 .617 .424
ln_Cost of Goods
Sold -.167 .063 -.191 -2.635 .009.726 -.146 -.08
0
a. Dependent Variable: ln_Expense: R&amp;D
Casewise Diagnosticsa
Case Number Std. Residual ln_Expense:
R&amp;D
Predicted Value Residual
44 -3.423 9.2103 13.434170 -4.2238696
93 -4.282 13.8155 19.099345 -5.2838453
142 -3.524 11.1563 15.505062 -4.3487624
290 -3.790 13.3047 17.981552 -4.6768525
a. Dependent Variable: ln_Expense: R&amp;D
Residuals Statisticsa
15

Minimum Maximum Mean Std. Deviation N
Predicted Value 9.347111 21.370089 16.296385 1.9104156 320
Std. Predicted Value -3.638 2.656 .000 1.000 320
Standard Error of
Predicted Value .069 .354 .112 .041 320
Adjusted Predicted Value 9.358300 21.379904 16.296820 1.9097661 320
Residual -5.2838454 2.6181247 0E-7 1.2300078 320
Std. Residual -4.282 2.122 .000 .997 320
Stud. Residual -4.306 2.128 .000 1.002 320
Deleted Residual -5.3436913 2.6344464 -.0004343 1.2426547 320
Stud. Deleted Residual -4.431 2.140 -.002 1.009 320
Mahal. Distance .002 25.216 1.994 2.774 320
Cook's Distance .000 .070 .003 .008 320
Centered Leverage Value .000 .079 .006 .009 320
a. Dependent Variable: ln_Expense: R&amp;D
16

17