Capital Budgeting Decision Analysis

This assignment delves into the world of capital budgeting, focusing on evaluating the viability of various projects. It presents a scenario with multiple projects and their associated cash flows. Students are tasked with analyzing these projects using common quantitative methods like Net Present Value (NPV), Internal Rate of Return (IRR), and Payback Period. The assignment emphasizes comparing the results of different methods and selecting the most viable projects, considering factors like timing and risk. Finally, it guides students through making a final decision by choosing the best set of projects for the company.

FINANCIAL MANAGEMENT

Contents
SOLUTION 1:.................................................................................................................................................................................................................................. 3
SOLUTION 2:.................................................................................................................................................................................................................................. 5
SOLUTION 3:................................................................................................................................................................................................................................ 11
SOLUTION 4:................................................................................................................................................................................................................................ 12
References................................................................................................................................................................................................................................... 13

SOLUTION 1:
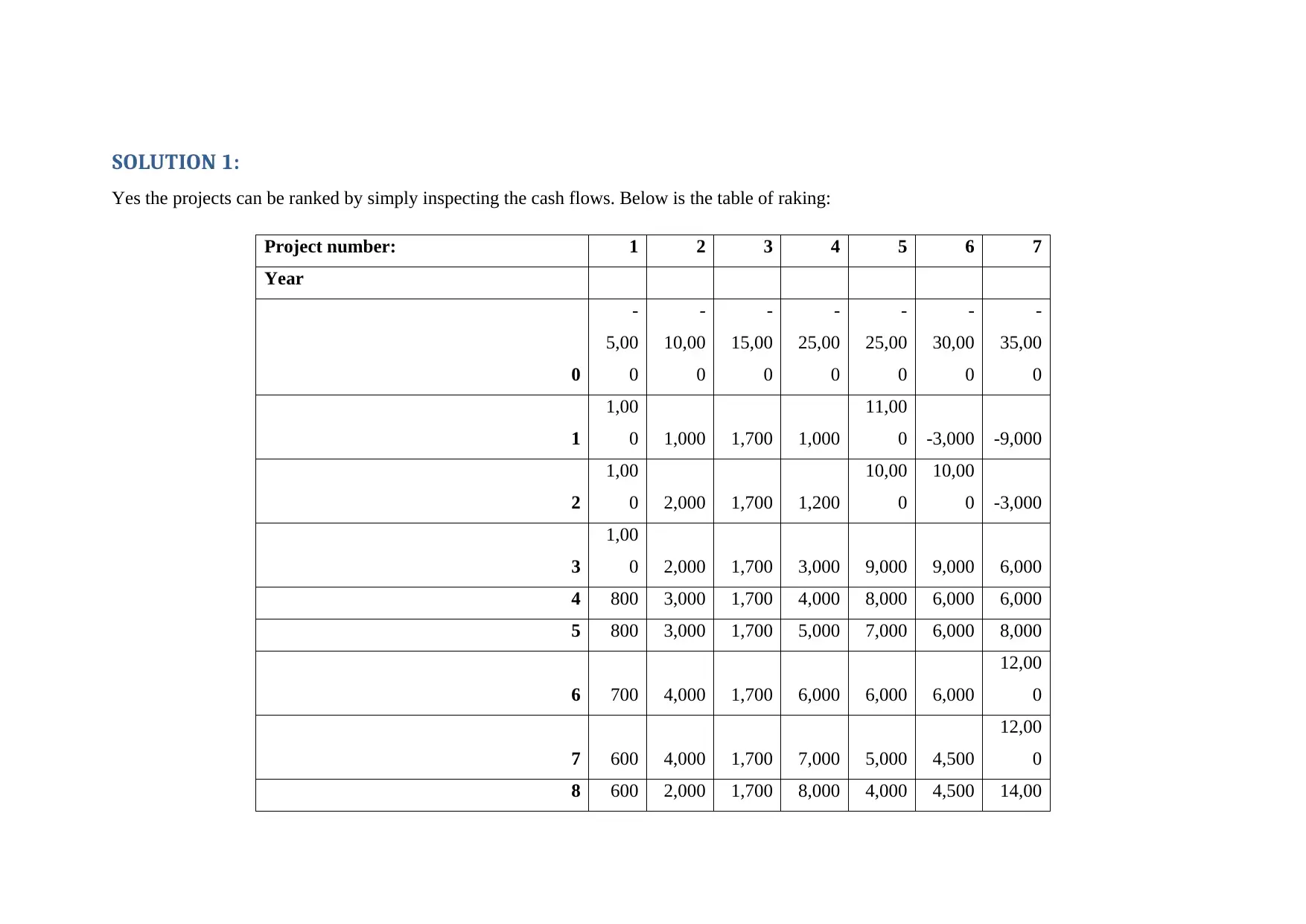
Yes the projects can be ranked by simply inspecting the cash flows. Below is the table of raking:
Project number: 1 2 3 4 5 6 7
Year
0
-
5,00
0
-
10,00
0
-
15,00
0
-
25,00
0
-
25,00
0
-
30,00
0
-
35,00
0
1
1,00
0 1,000 1,700 1,000
11,00
0 -3,000 -9,000
2
1,00
0 2,000 1,700 1,200
10,00
0
10,00
0 -3,000
3
1,00
0 2,000 1,700 3,000 9,000 9,000 6,000
4 800 3,000 1,700 4,000 8,000 6,000 6,000
5 800 3,000 1,700 5,000 7,000 6,000 8,000
6 700 4,000 1,700 6,000 6,000 6,000
12,00
0
7 600 4,000 1,700 7,000 5,000 4,500
12,00
0
8 600 2,000 1,700 8,000 4,000 4,500 14,00

0
9 500 2,000 1,700 9,000 3,000 3,000
14,00
0
10 500 2,000 1,700
11,00
0 -5,000 3,000
14,00
0
Sum of cash-flow benefits
7,50
0
25,00
0
17,00
0
55,20
0
58,00
0
49,00
0
74,00
0
Excess of cash flow over initial
investment
2,50
0
15,00
0 2,000
30,20
0
33,00
0
19,00
0
39,00
0
Ranking 6 5 7 3 2 4 1
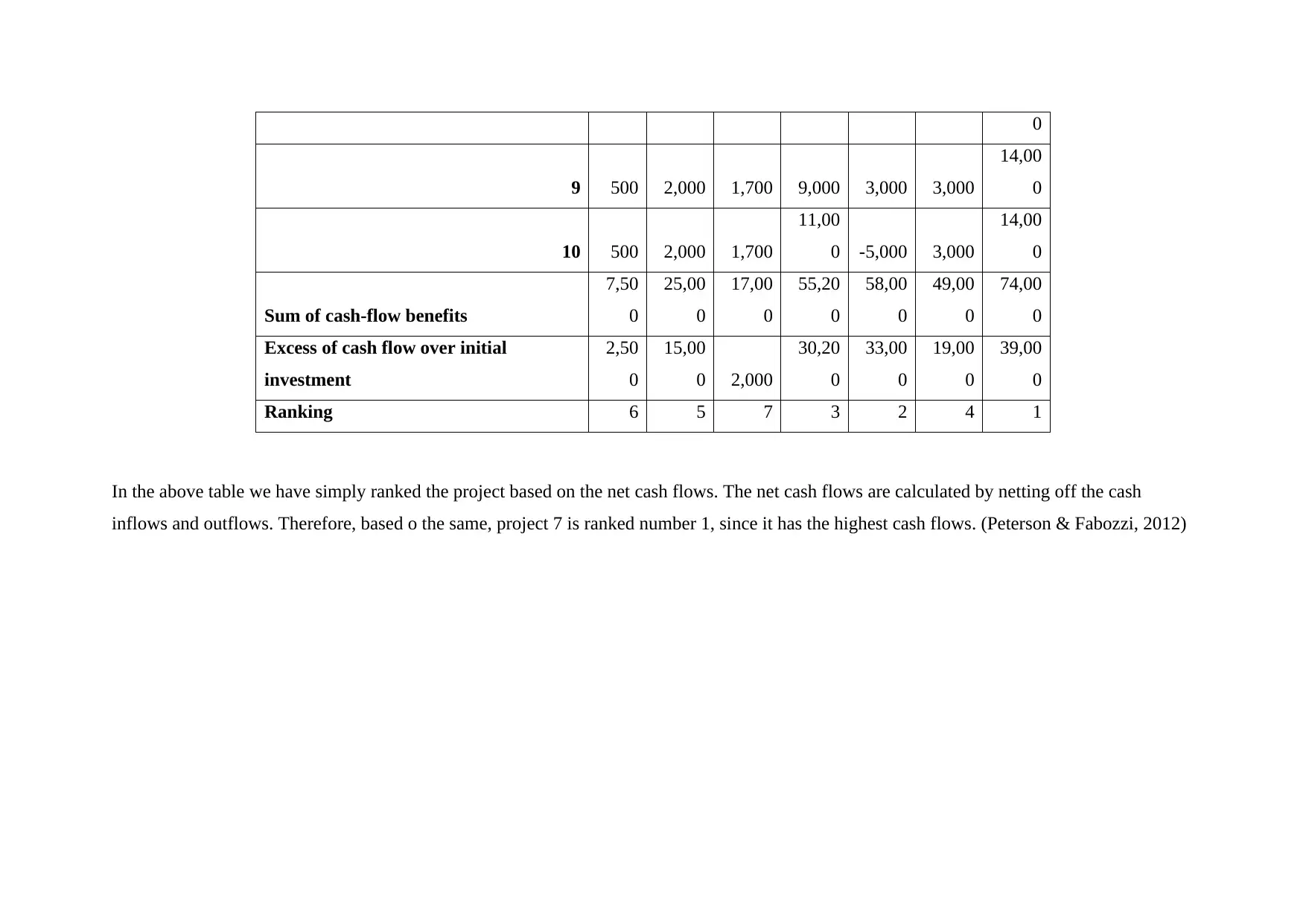
In the above table we have simply ranked the project based on the net cash flows. The net cash flows are calculated by netting off the cash
inflows and outflows. Therefore, based o the same, project 7 is ranked number 1, since it has the highest cash flows. (Peterson & Fabozzi, 2012)

SOLUTION 2:
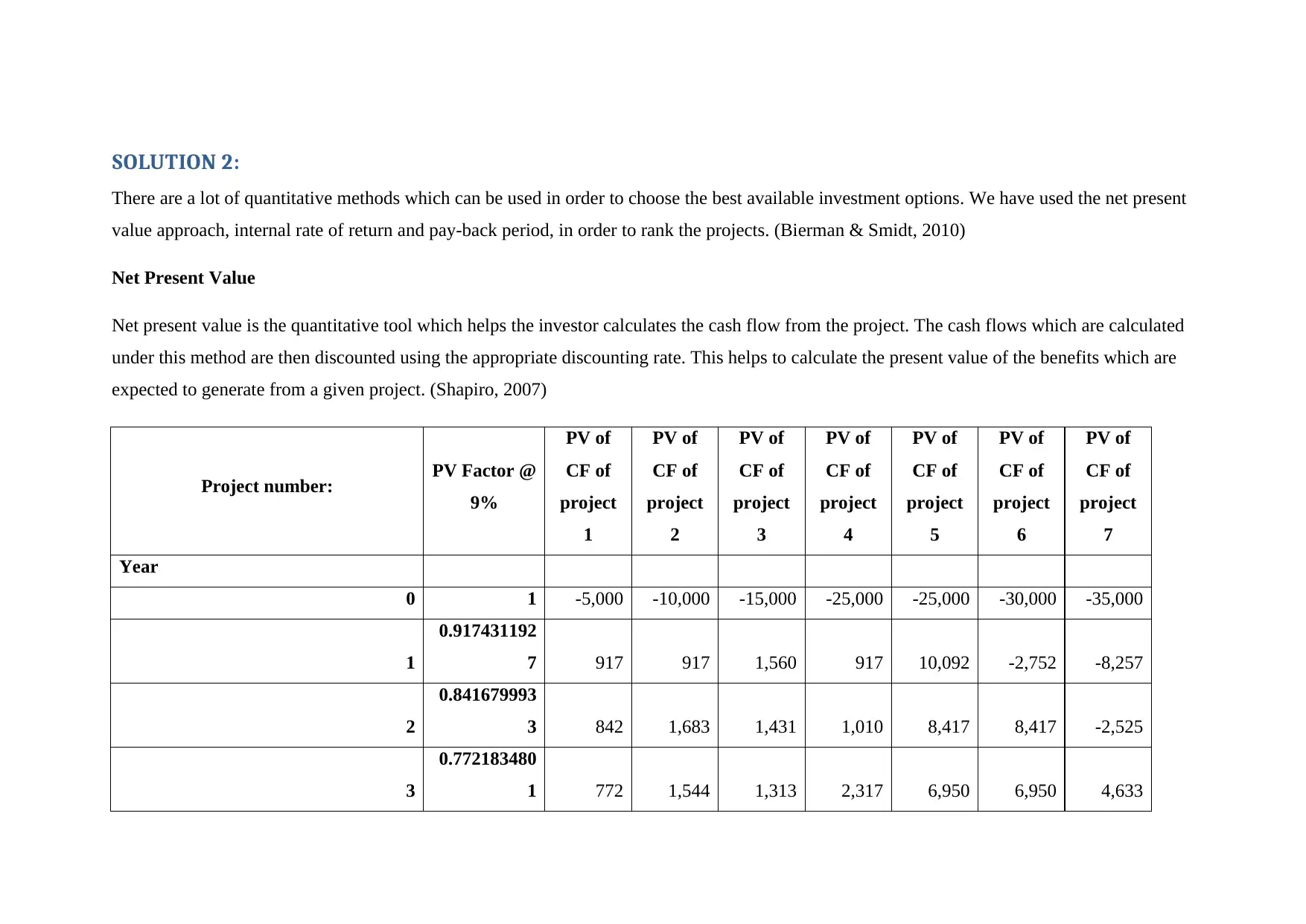
There are a lot of quantitative methods which can be used in order to choose the best available investment options. We have used the net present
value approach, internal rate of return and pay-back period, in order to rank the projects. (Bierman & Smidt, 2010)
Net Present Value
Net present value is the quantitative tool which helps the investor calculates the cash flow from the project. The cash flows which are calculated
under this method are then discounted using the appropriate discounting rate. This helps to calculate the present value of the benefits which are
expected to generate from a given project. (Shapiro, 2007)
Project number: PV Factor @
9%
PV of
CF of
project
1
PV of
CF of
project
2
PV of
CF of
project
3
PV of
CF of
project
4
PV of
CF of
project
5
PV of
CF of
project
6
PV of
CF of
project
7
Year
0 1 -5,000 -10,000 -15,000 -25,000 -25,000 -30,000 -35,000
1
0.917431192
7 917 917 1,560 917 10,092 -2,752 -8,257
2
0.841679993
3 842 1,683 1,431 1,010 8,417 8,417 -2,525
3
0.772183480
1 772 1,544 1,313 2,317 6,950 6,950 4,633

4
0.708425211
1 567 2,125 1,204 2,834 5,667 4,251 4,251
5
0.649931386
3 520 1,950 1,105 3,250 4,550 3,900 5,199
6
0.596267326
9 417 2,385 1,014 3,578 3,578 3,578 7,155
7
0.547034244
8 328 2,188 930 3,829 2,735 2,462 6,564
8
0.501866279
7 301 1,004 853 4,015 2,007 2,258 7,026
9
0.460427779
5 230 921 783 4,144 1,381 1,381 6,446
10
0.422410806
9 211 845 718 4,647 -2,112 1,267 5,914
Sum of cash-flow benefits 5,106 15,563 10,910 30,539 43,265 31,710 36,407
Excess of cash flow over initial
investment 106 5,563 -4,090 5,539 18,265 1,710 1,407
Excess of cash flow over initial
investment 6 2 7 3 1 4 5

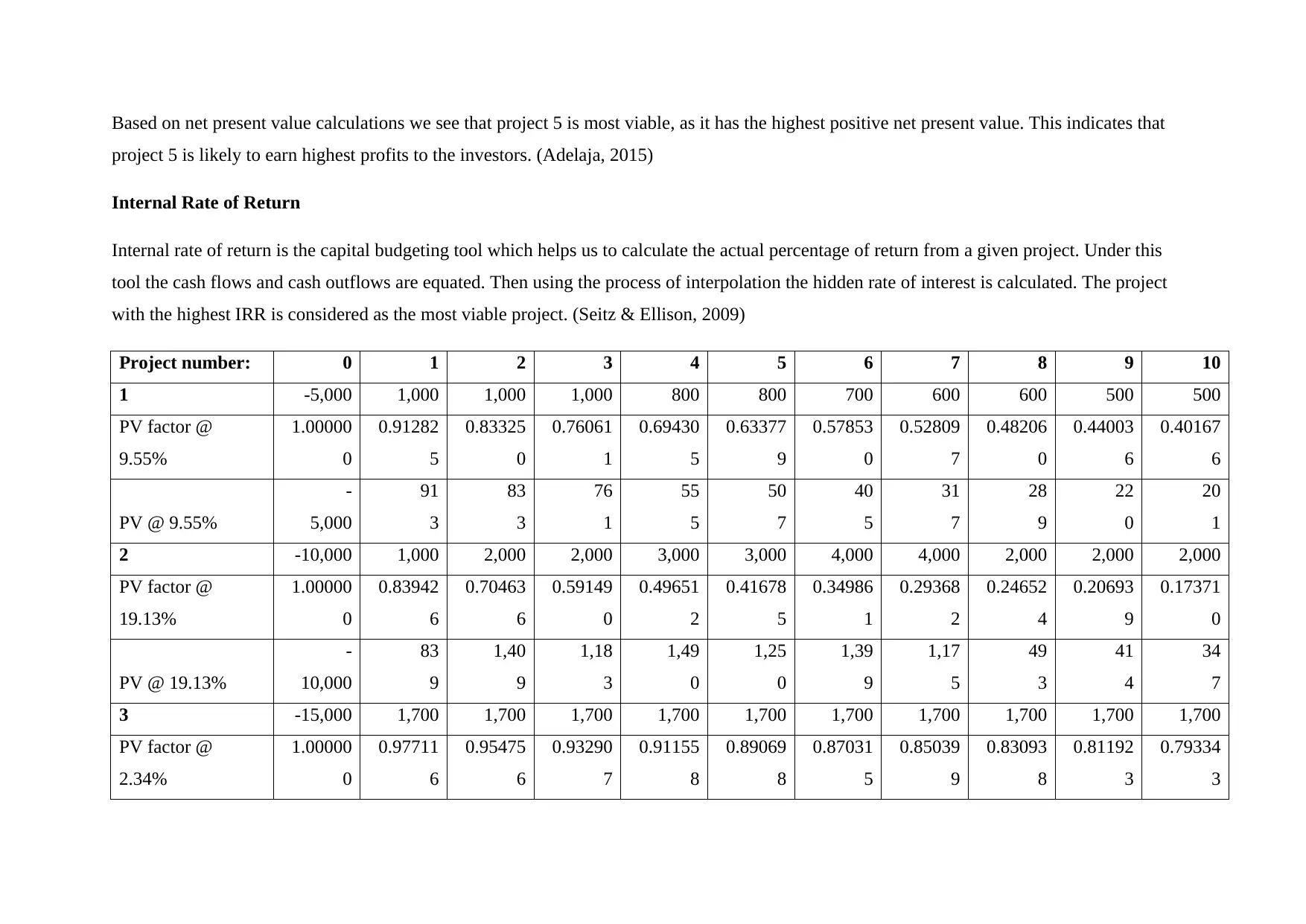
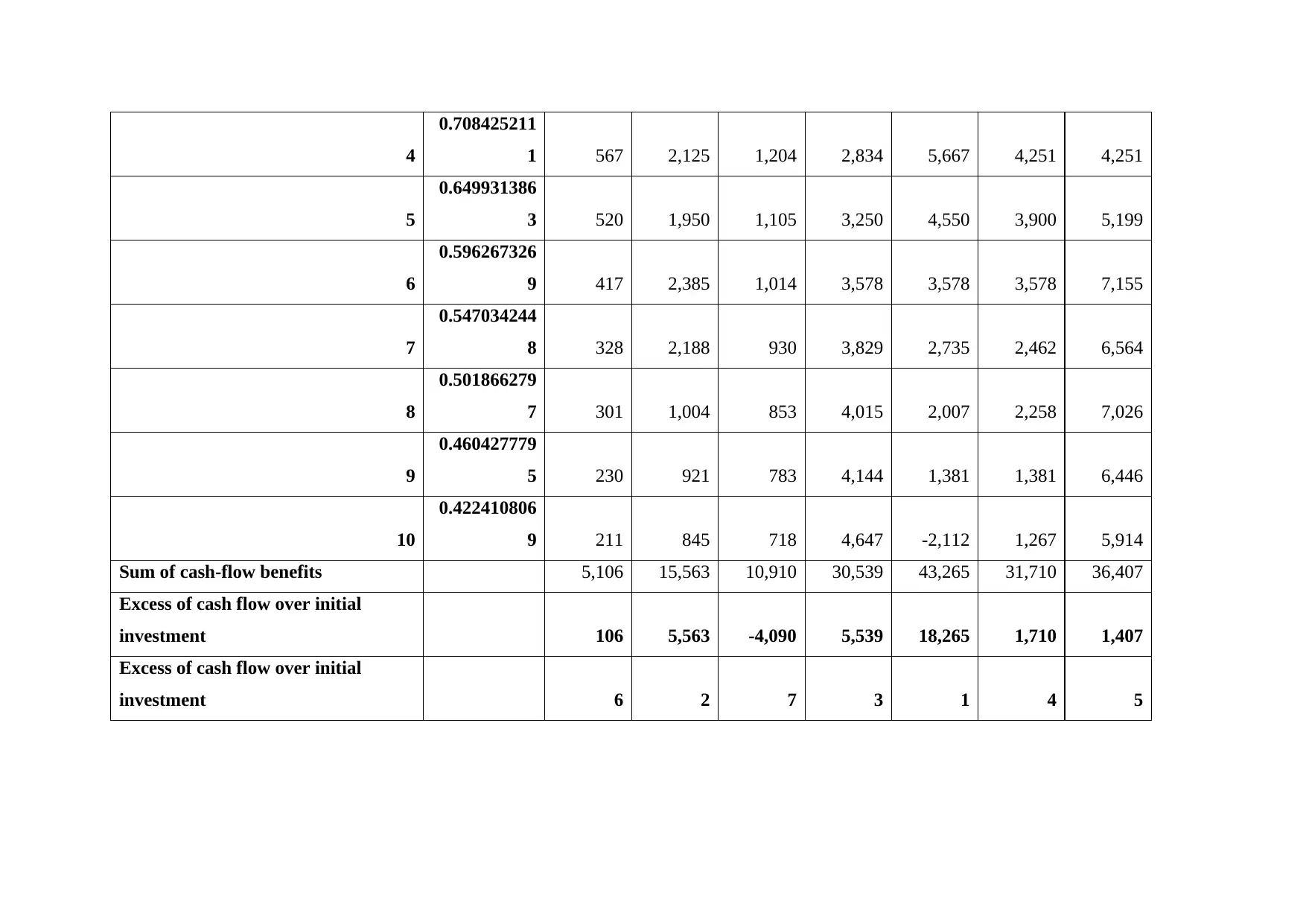
Based on net present value calculations we see that project 5 is most viable, as it has the highest positive net present value. This indicates that
project 5 is likely to earn highest profits to the investors. (Adelaja, 2015)
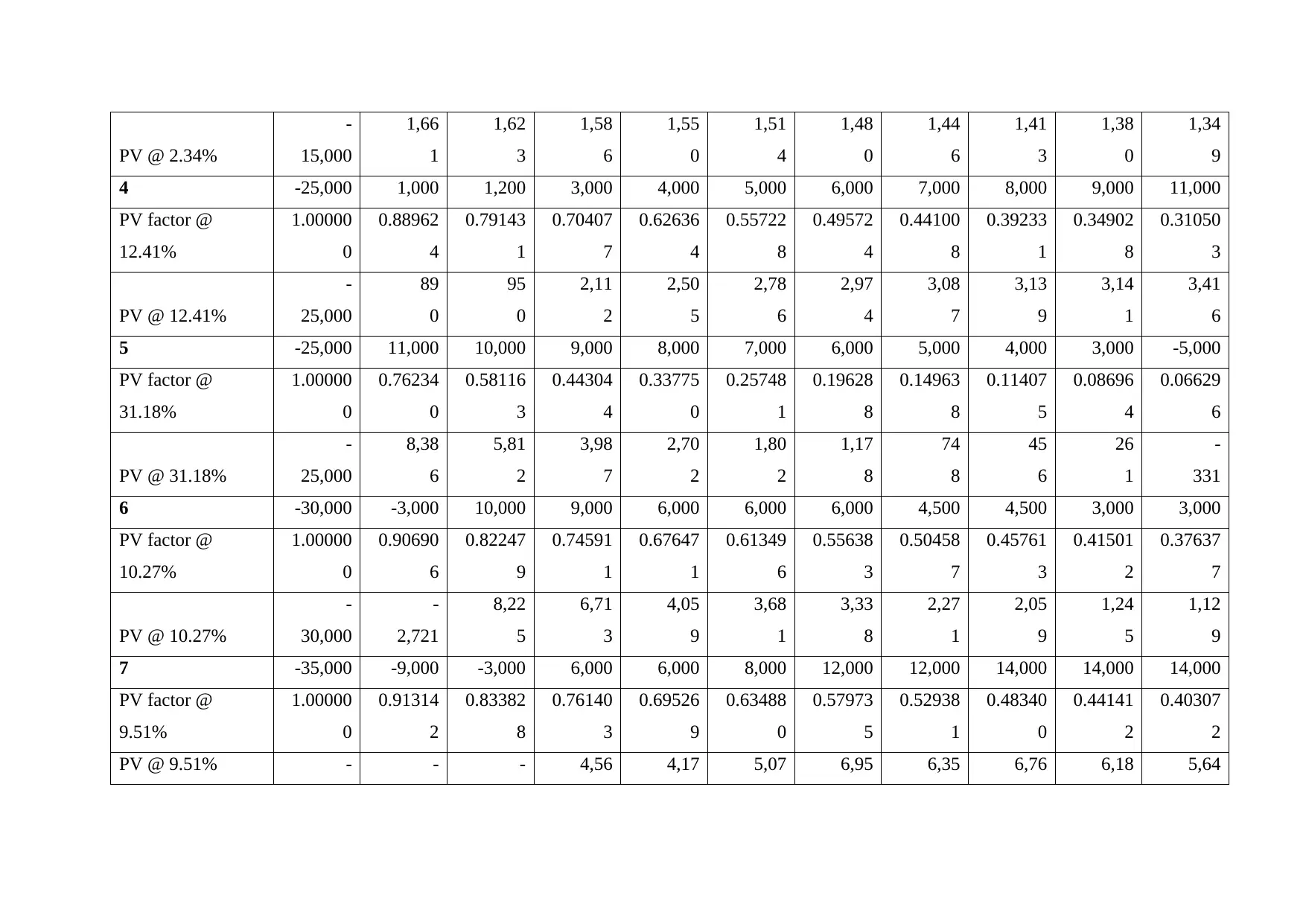
Internal Rate of Return
Internal rate of return is the capital budgeting tool which helps us to calculate the actual percentage of return from a given project. Under this
tool the cash flows and cash outflows are equated. Then using the process of interpolation the hidden rate of interest is calculated. The project
with the highest IRR is considered as the most viable project. (Seitz & Ellison, 2009)
Project number: 0 1 2 3 4 5 6 7 8 9 10
1 -5,000 1,000 1,000 1,000 800 800 700 600 600 500 500
PV factor @
9.55%
1.00000
0
0.91282
5
0.83325
0
0.76061
1
0.69430
5
0.63377
9
0.57853
0
0.52809
7
0.48206
0
0.44003
6
0.40167
6
PV @ 9.55%
-
5,000
91
3
83
3
76
1
55
5
50
7
40
5
31
7
28
9
22
0
20
1
2 -10,000 1,000 2,000 2,000 3,000 3,000 4,000 4,000 2,000 2,000 2,000
PV factor @
19.13%
1.00000
0
0.83942
6
0.70463
6
0.59149
0
0.49651
2
0.41678
5
0.34986
1
0.29368
2
0.24652
4
0.20693
9
0.17371
0
PV @ 19.13%
-
10,000
83
9
1,40
9
1,18
3
1,49
0
1,25
0
1,39
9
1,17
5
49
3
41
4
34
7
3 -15,000 1,700 1,700 1,700 1,700 1,700 1,700 1,700 1,700 1,700 1,700
PV factor @
2.34%
1.00000
0
0.97711
6
0.95475
6
0.93290
7
0.91155
8
0.89069
8
0.87031
5
0.85039
9
0.83093
8
0.81192
3
0.79334
3

PV @ 2.34%
-
15,000
1,66
1
1,62
3
1,58
6
1,55
0
1,51
4
1,48
0
1,44
6
1,41
3
1,38
0
1,34
9
4 -25,000 1,000 1,200 3,000 4,000 5,000 6,000 7,000 8,000 9,000 11,000
PV factor @
12.41%
1.00000
0
0.88962
4
0.79143
1
0.70407
7
0.62636
4
0.55722
8
0.49572
4
0.44100
8
0.39233
1
0.34902
8
0.31050
3
PV @ 12.41%
-
25,000
89
0
95
0
2,11
2
2,50
5
2,78
6
2,97
4
3,08
7
3,13
9
3,14
1
3,41
6
5 -25,000 11,000 10,000 9,000 8,000 7,000 6,000 5,000 4,000 3,000 -5,000
PV factor @
31.18%
1.00000
0
0.76234
0
0.58116
3
0.44304
4
0.33775
0
0.25748
1
0.19628
8
0.14963
8
0.11407
5
0.08696
4
0.06629
6
PV @ 31.18%
-
25,000
8,38
6
5,81
2
3,98
7
2,70
2
1,80
2
1,17
8
74
8
45
6
26
1
-
331
6 -30,000 -3,000 10,000 9,000 6,000 6,000 6,000 4,500 4,500 3,000 3,000
PV factor @
10.27%
1.00000
0
0.90690
6
0.82247
9
0.74591
1
0.67647
1
0.61349
6
0.55638
3
0.50458
7
0.45761
3
0.41501
2
0.37637
7
PV @ 10.27%
-
30,000
-
2,721
8,22
5
6,71
3
4,05
9
3,68
1
3,33
8
2,27
1
2,05
9
1,24
5
1,12
9
7 -35,000 -9,000 -3,000 6,000 6,000 8,000 12,000 12,000 14,000 14,000 14,000
PV factor @
9.51%
1.00000
0
0.91314
2
0.83382
8
0.76140
3
0.69526
9
0.63488
0
0.57973
5
0.52938
1
0.48340
0
0.44141
2
0.40307
2
PV @ 9.51% - - - 4,56 4,17 5,07 6,95 6,35 6,76 6,18 5,64

35,000 8,218 2,501 8 2 9 7 3 8 0 3
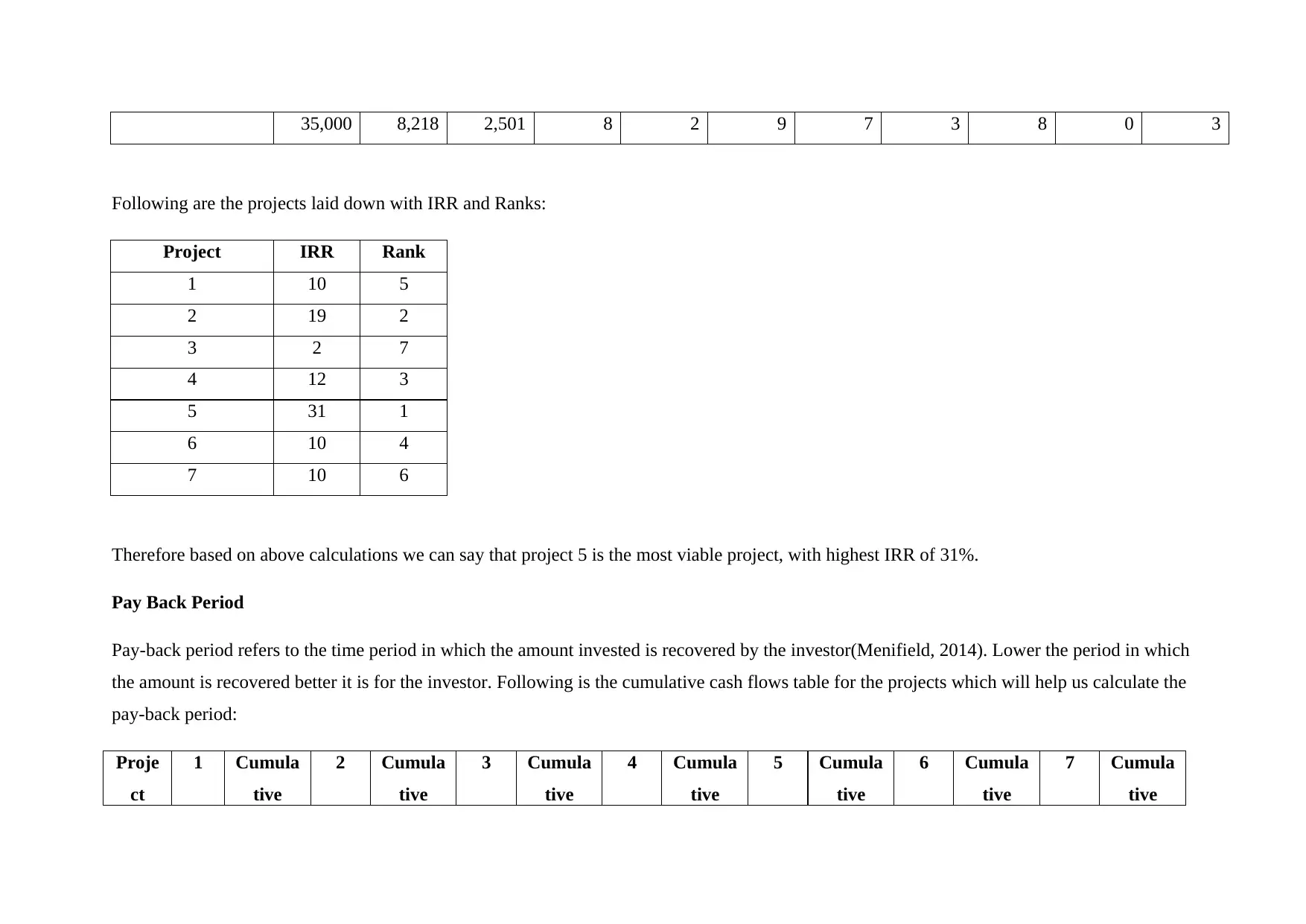
Following are the projects laid down with IRR and Ranks:
Project IRR Rank
1 10 5
2 19 2
3 2 7
4 12 3
5 31 1
6 10 4
7 10 6
Therefore based on above calculations we can say that project 5 is the most viable project, with highest IRR of 31%.
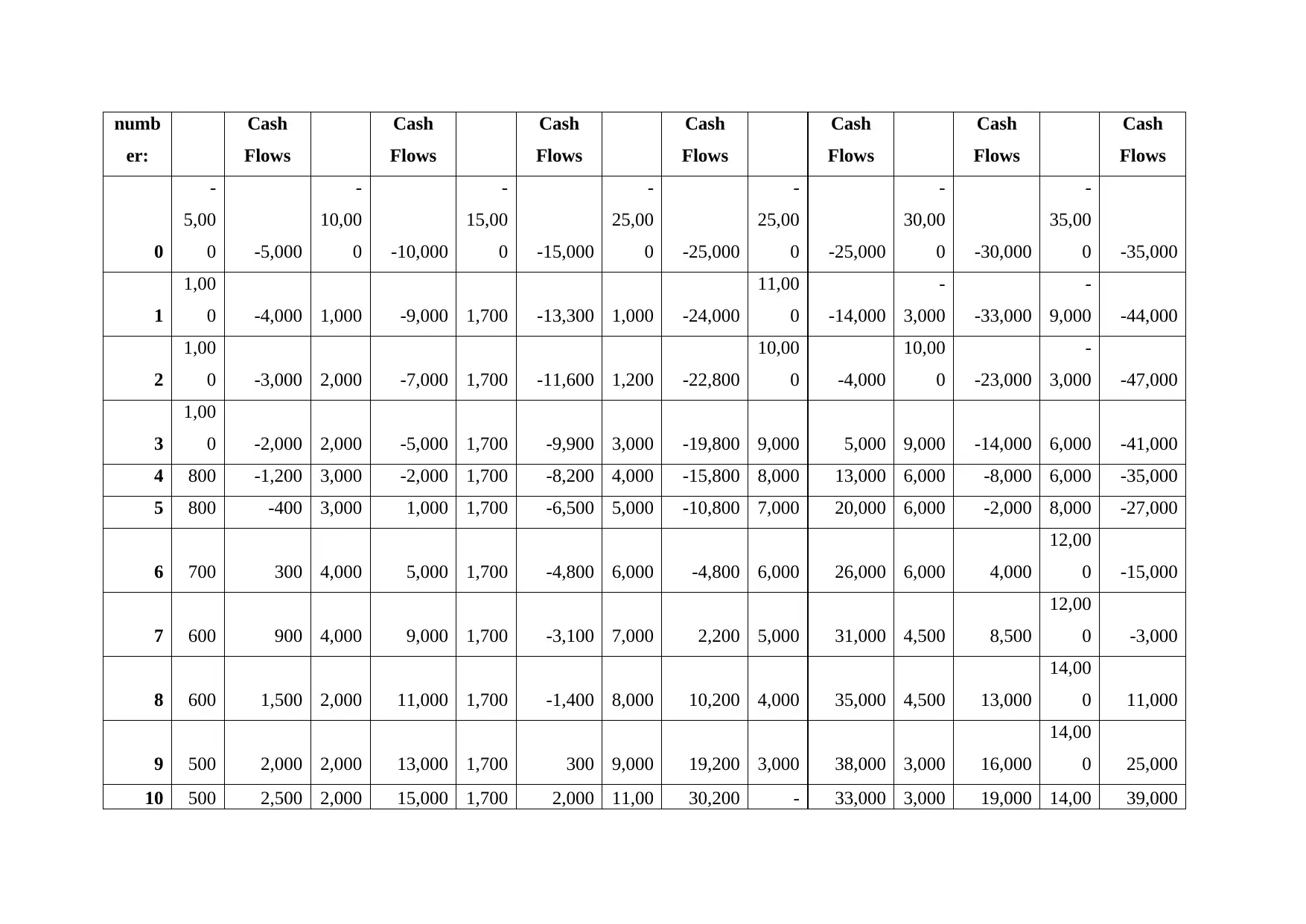
Pay Back Period
Pay-back period refers to the time period in which the amount invested is recovered by the investor(Menifield, 2014). Lower the period in which
the amount is recovered better it is for the investor. Following is the cumulative cash flows table for the projects which will help us calculate the
pay-back period:
Proje
ct
1 Cumula
tive
2 Cumula
tive
3 Cumula
tive
4 Cumula
tive
5 Cumula
tive
6 Cumula
tive
7 Cumula
tive

numb
er:
Cash
Flows
Cash
Flows
Cash
Flows
Cash
Flows
Cash
Flows
Cash
Flows
Cash
Flows
0
-
5,00
0 -5,000
-
10,00
0 -10,000
-
15,00
0 -15,000
-
25,00
0 -25,000
-
25,00
0 -25,000
-
30,00
0 -30,000
-
35,00
0 -35,000
1
1,00
0 -4,000 1,000 -9,000 1,700 -13,300 1,000 -24,000
11,00
0 -14,000
-
3,000 -33,000
-
9,000 -44,000
2
1,00
0 -3,000 2,000 -7,000 1,700 -11,600 1,200 -22,800
10,00
0 -4,000
10,00
0 -23,000
-
3,000 -47,000
3
1,00
0 -2,000 2,000 -5,000 1,700 -9,900 3,000 -19,800 9,000 5,000 9,000 -14,000 6,000 -41,000
4 800 -1,200 3,000 -2,000 1,700 -8,200 4,000 -15,800 8,000 13,000 6,000 -8,000 6,000 -35,000
5 800 -400 3,000 1,000 1,700 -6,500 5,000 -10,800 7,000 20,000 6,000 -2,000 8,000 -27,000
6 700 300 4,000 5,000 1,700 -4,800 6,000 -4,800 6,000 26,000 6,000 4,000
12,00
0 -15,000
7 600 900 4,000 9,000 1,700 -3,100 7,000 2,200 5,000 31,000 4,500 8,500
12,00
0 -3,000
8 600 1,500 2,000 11,000 1,700 -1,400 8,000 10,200 4,000 35,000 4,500 13,000
14,00
0 11,000
9 500 2,000 2,000 13,000 1,700 300 9,000 19,200 3,000 38,000 3,000 16,000
14,00
0 25,000
10 500 2,500 2,000 15,000 1,700 2,000 11,00 30,200 - 33,000 3,000 19,000 14,00 39,000

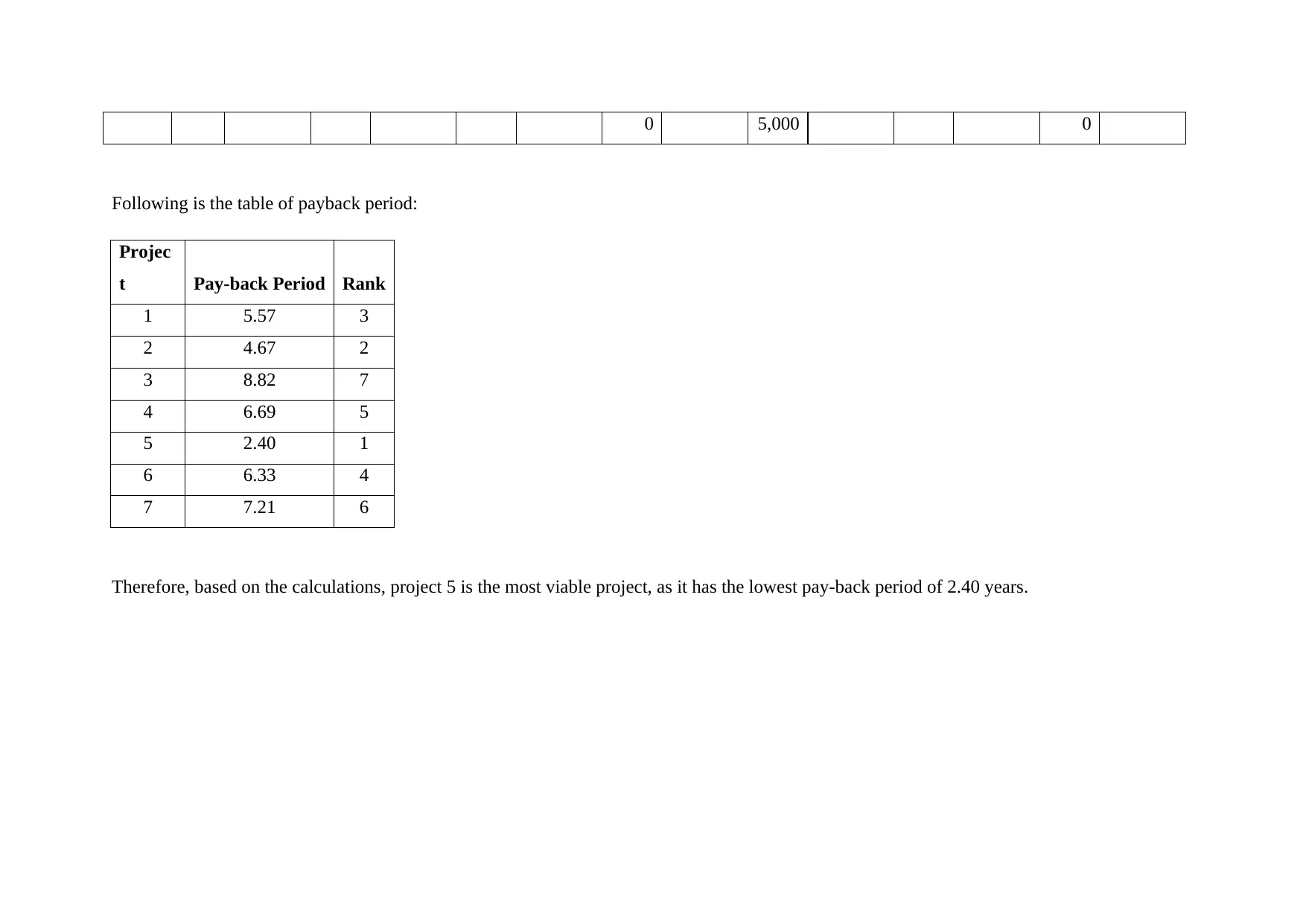
0 5,000 0
Following is the table of payback period:
Projec
t Pay-back Period Rank
1 5.57 3
2 4.67 2
3 8.82 7
4 6.69 5
5 2.40 1
6 6.33 4
7 7.21 6
Therefore, based on the calculations, project 5 is the most viable project, as it has the lowest pay-back period of 2.40 years.

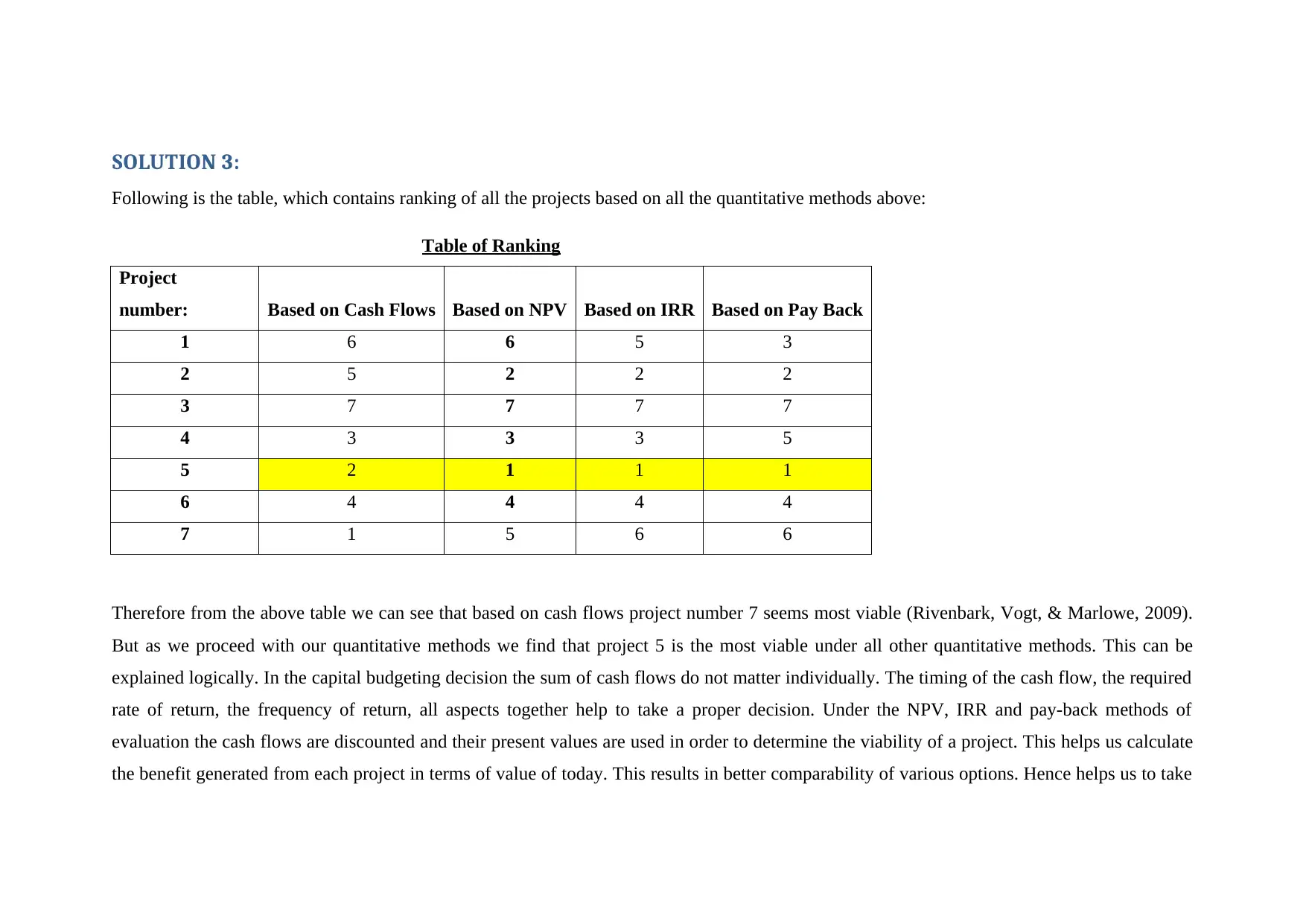
SOLUTION 3:
Following is the table, which contains ranking of all the projects based on all the quantitative methods above:
Table of Ranking
Project
number: Based on Cash Flows Based on NPV Based on IRR Based on Pay Back
1 6 6 5 3
2 5 2 2 2
3 7 7 7 7
4 3 3 3 5
5 2 1 1 1
6 4 4 4 4
7 1 5 6 6
Therefore from the above table we can see that based on cash flows project number 7 seems most viable (Rivenbark, Vogt, & Marlowe, 2009).
But as we proceed with our quantitative methods we find that project 5 is the most viable under all other quantitative methods. This can be
explained logically. In the capital budgeting decision the sum of cash flows do not matter individually. The timing of the cash flow, the required
rate of return, the frequency of return, all aspects together help to take a proper decision. Under the NPV, IRR and pay-back methods of
evaluation the cash flows are discounted and their present values are used in order to determine the viability of a project. This helps us calculate
the benefit generated from each project in terms of value of today. This results in better comparability of various options. Hence helps us to take

the correct decision. Therefore, this is the reason the ranking are not same under the methods. (Dayananda, Irons, Harrison, Herbohn, &
Rowland, 2008)

SOLUTION 4:
Based on our evaluation above we see that project 5, 4 and 6 are the top most projects with highest ranking under all the quantitative methods.
But, since projects 4 and 5 are mutually exclusive; we can select only one form these two. Since project 5 is has better performance than project
4, we opt of project 5. Also, now we need to select the next best available option, which is project number 2. Therefore the three best projects
that the company should accept are project number 5, 6 and 2.