SIT718 Assessment Task 2: The Behavior and Performance of Share Prices
VerifiedAdded on 2023/05/30
|8
|494
|278
Project
AI Summary
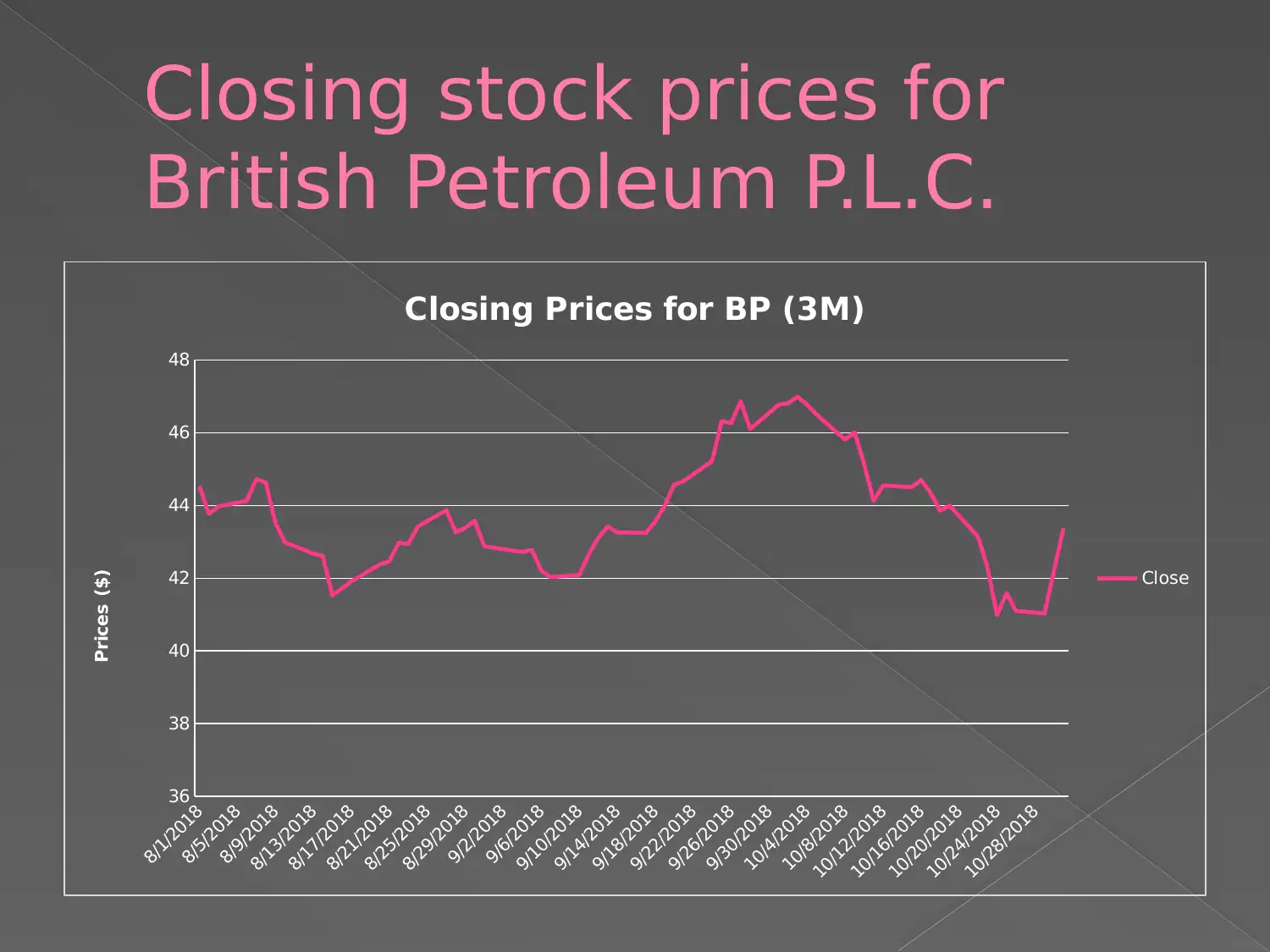
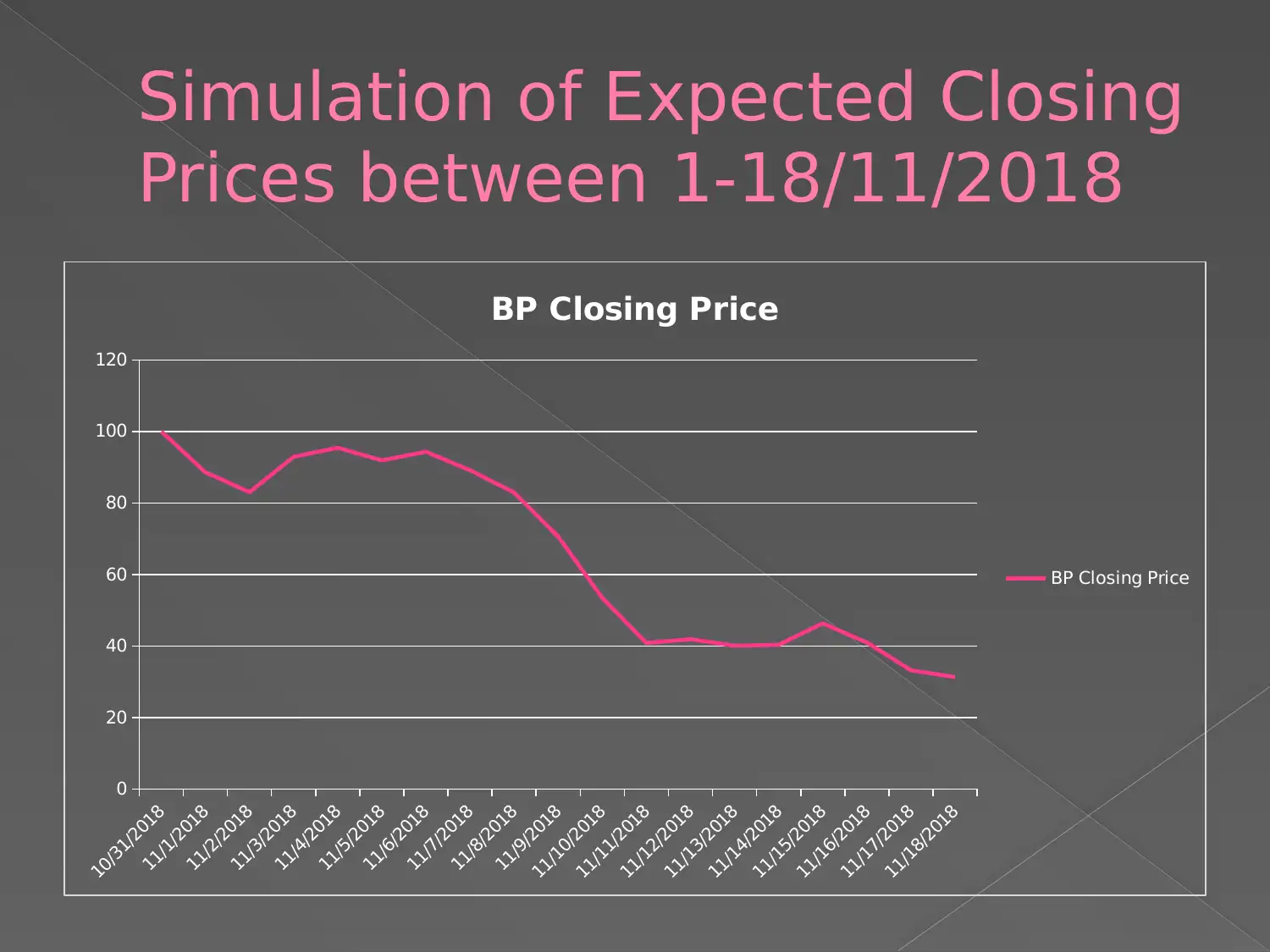
This assignment analyzes the behavior and performance of British Petroleum (BP) share prices using historical data and the stochastic model of Geometric Brownian Motion. The analysis involves understanding the concepts of drift (Mu) and diffusion (Sigma) and their time-dependent nature. The assignment assesses the stability of the market by examining the standard deviation of share prices and the duration over which the data was collected. The results show that the share prices satisfy the necessary Geometric Brownian Motion conditions. The assignment also includes simulations of expected closing prices and provides relevant references. The goal is to apply knowledge of multivariate functions, data transformations, and data distributions to summarize the dataset and develop software codes to solve computational problems for real-world analytics. The project also aims to demonstrate professional ethics in working with real-world data, as outlined in the assessment brief for SIT718 Real World Analytics Assessment Task 2.
1 out of 8













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)