Statistics Assignment: Data Analysis, Interpretation, and Finance
VerifiedAdded on 2020/07/22
|18
|1639
|163
Homework Assignment
AI Summary
This statistics assignment solution covers various statistical concepts and their applications. It begins with scatter plots, z-scores, and ranking based on given data, followed by pivot table analysis and graphical presentations to examine the relationship between variables. The assignment explores hypothesis testing at a 5% significance level, including the calculation of p-values and conclusions regarding null hypotheses. Further sections involve pivot tables, graphical representations, and comments on variable relationships, along with calculations for sample means, z-scores, and ranking. Confidence intervals are determined, and a custom dataset is created for summarizing variables. Finally, the assignment discusses the use of mean and standard deviations in finance, demonstrating their utility in evaluating large datasets and making informed decisions. The solution provides detailed steps, calculations, and interpretations for each section, offering a comprehensive understanding of statistical methods.

Statistics
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

TABLE OF CONTENTS
SECTION 1.....................................................................................................................................1
a. Presenting scatter plot on the basis of given data set...............................................................1
b. Estimating annual contribution if income is $200,000............................................................1
c. Finding Z score........................................................................................................................1
d. Assessing P(Z < zscore)...........................................................................................................2
e. Ranking....................................................................................................................................2
SECTION 2.....................................................................................................................................3
a. Pivot table by using excel........................................................................................................3
b. Graphical presentation.............................................................................................................4
c. Commenting on the relationship takes place between the two variables.................................4
d...................................................................................................................................................4
1. Stating the deviations take place in the sample proportion.....................................................4
2. Assessing the value of Z score.................................................................................................4
3. Determining P(Z<zscore)........................................................................................................5
4. Give ranking on the basis of estimation..................................................................................5
e. Testing there is a difference in the proportions @ 5% level of significance...........................6
1. Stating hypothesis....................................................................................................................6
2. Finding p value........................................................................................................................6
3. Stating whether null hypothesis is true or false.......................................................................7
4. Conclusion...............................................................................................................................8
SECTION 3.....................................................................................................................................8
a. Creating a pivot table for summarizing statistical information...............................................8
b. Creating appropriate graph to show the relationship between the variables...........................8
c. Commenting on the relationship between the variables..........................................................9
SECTION 1.....................................................................................................................................1
a. Presenting scatter plot on the basis of given data set...............................................................1
b. Estimating annual contribution if income is $200,000............................................................1
c. Finding Z score........................................................................................................................1
d. Assessing P(Z < zscore)...........................................................................................................2
e. Ranking....................................................................................................................................2
SECTION 2.....................................................................................................................................3
a. Pivot table by using excel........................................................................................................3
b. Graphical presentation.............................................................................................................4
c. Commenting on the relationship takes place between the two variables.................................4
d...................................................................................................................................................4
1. Stating the deviations take place in the sample proportion.....................................................4
2. Assessing the value of Z score.................................................................................................4
3. Determining P(Z<zscore)........................................................................................................5
4. Give ranking on the basis of estimation..................................................................................5
e. Testing there is a difference in the proportions @ 5% level of significance...........................6
1. Stating hypothesis....................................................................................................................6
2. Finding p value........................................................................................................................6
3. Stating whether null hypothesis is true or false.......................................................................7
4. Conclusion...............................................................................................................................8
SECTION 3.....................................................................................................................................8
a. Creating a pivot table for summarizing statistical information...............................................8
b. Creating appropriate graph to show the relationship between the variables...........................8
c. Commenting on the relationship between the variables..........................................................9

d...................................................................................................................................................9
1. Difference between the sample means x 1-x 2.........................................................................9
2. Z-score.....................................................................................................................................9
3.................................................................................................................................................10
4.................................................................................................................................................10
e. Testing significant differences in the mean value @ 5% level of significance.....................11
1. Hypothesis.............................................................................................................................11
2.................................................................................................................................................11
3.................................................................................................................................................11
4.................................................................................................................................................11
SECTION 4...................................................................................................................................12
a..................................................................................................................................................12
b.................................................................................................................................................12
c. Assessing Z score...................................................................................................................12
1.................................................................................................................................................12
2.................................................................................................................................................12
3. Ranking..................................................................................................................................13
d. Finding 95% confidence interval level for the people who support change..........................13
SECTION 5...................................................................................................................................14
A and c Creating or obtaining own data set...............................................................................14
b. Summarizing variables by using pivot table..........................................................................14
SECTION 6...................................................................................................................................15
Discussing the manner in which mean and standard deviations are used in finance.................15
1. Difference between the sample means x 1-x 2.........................................................................9
2. Z-score.....................................................................................................................................9
3.................................................................................................................................................10
4.................................................................................................................................................10
e. Testing significant differences in the mean value @ 5% level of significance.....................11
1. Hypothesis.............................................................................................................................11
2.................................................................................................................................................11
3.................................................................................................................................................11
4.................................................................................................................................................11
SECTION 4...................................................................................................................................12
a..................................................................................................................................................12
b.................................................................................................................................................12
c. Assessing Z score...................................................................................................................12
1.................................................................................................................................................12
2.................................................................................................................................................12
3. Ranking..................................................................................................................................13
d. Finding 95% confidence interval level for the people who support change..........................13
SECTION 5...................................................................................................................................14
A and c Creating or obtaining own data set...............................................................................14
b. Summarizing variables by using pivot table..........................................................................14
SECTION 6...................................................................................................................................15
Discussing the manner in which mean and standard deviations are used in finance.................15
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
SECTION 1
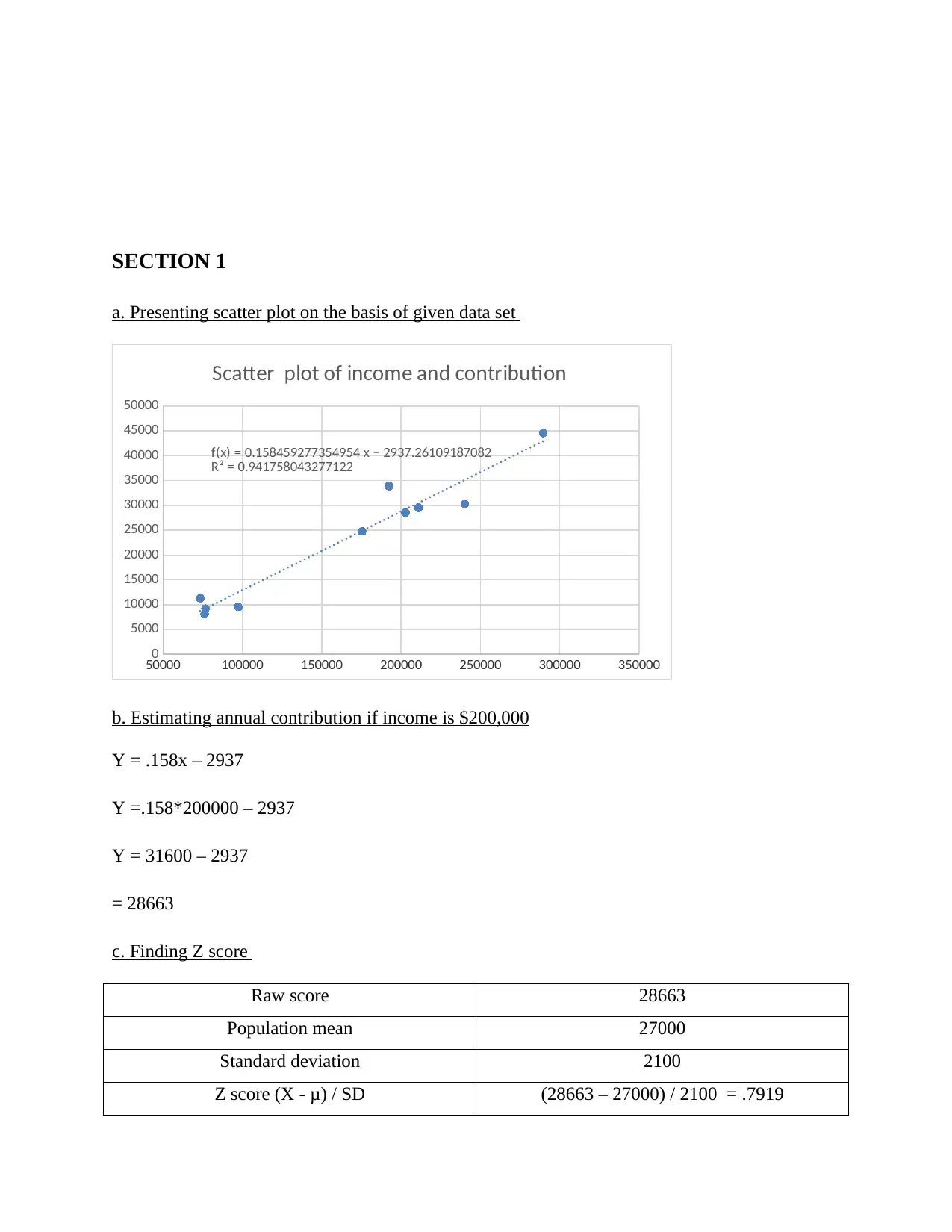
a. Presenting scatter plot on the basis of given data set
50000 100000 150000 200000 250000 300000 350000
0
5000
10000
15000
20000
25000
30000
35000
40000
45000
50000
f(x) = 0.158459277354954 x − 2937.26109187082
R² = 0.941758043277122
Scatter plot of income and contribution
b. Estimating annual contribution if income is $200,000
Y = .158x – 2937
Y =.158*200000 – 2937
Y = 31600 – 2937
= 28663
c. Finding Z score
Raw score 28663
Population mean 27000
Standard deviation 2100
Z score (X - μ) / SD (28663 – 27000) / 2100 = .7919
a. Presenting scatter plot on the basis of given data set
50000 100000 150000 200000 250000 300000 350000
0
5000
10000
15000
20000
25000
30000
35000
40000
45000
50000
f(x) = 0.158459277354954 x − 2937.26109187082
R² = 0.941758043277122
Scatter plot of income and contribution
b. Estimating annual contribution if income is $200,000
Y = .158x – 2937
Y =.158*200000 – 2937
Y = 31600 – 2937
= 28663
c. Finding Z score
Raw score 28663
Population mean 27000
Standard deviation 2100
Z score (X - μ) / SD (28663 – 27000) / 2100 = .7919
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
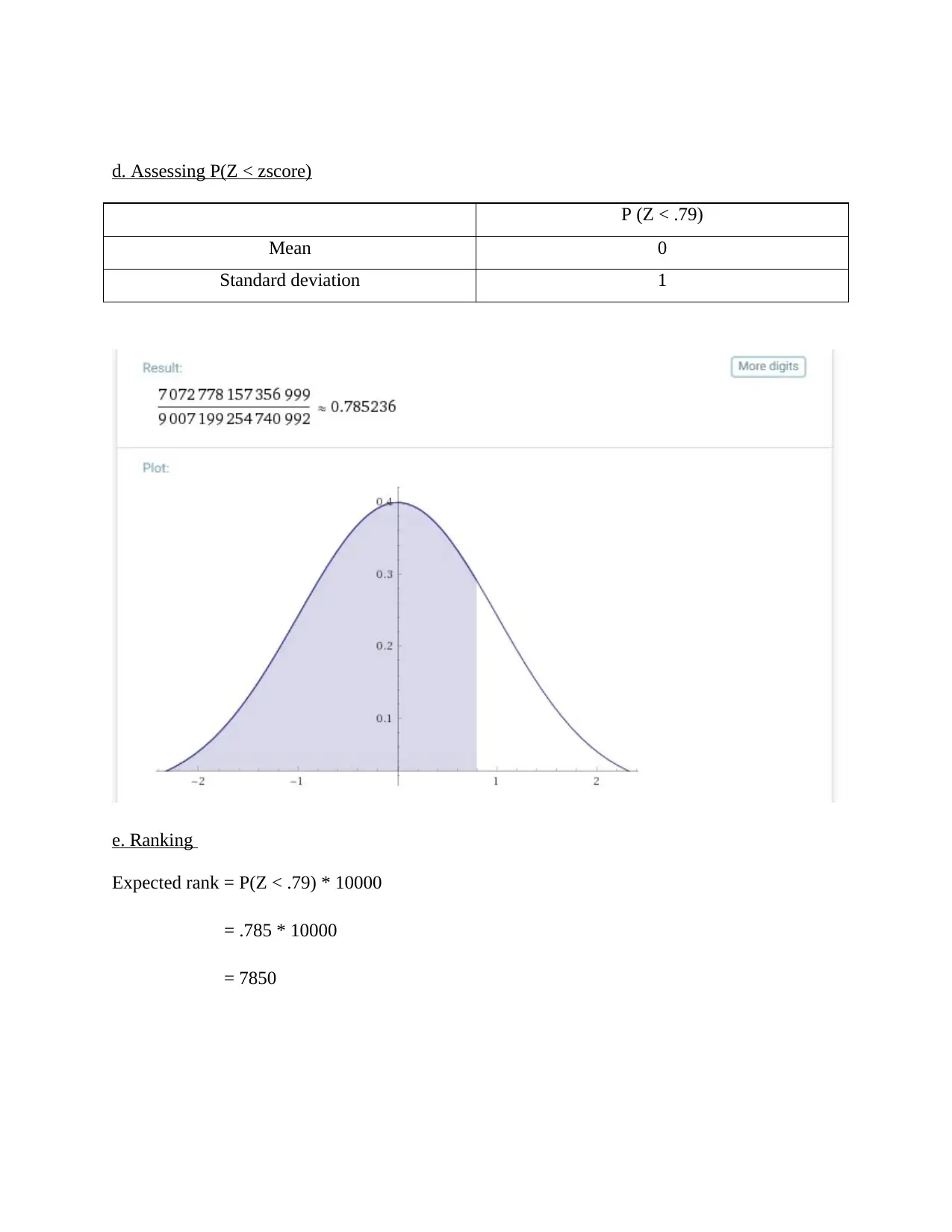
d. Assessing P(Z < zscore)
P (Z < .79)
Mean 0
Standard deviation 1
e. Ranking
Expected rank = P(Z < .79) * 10000
= .785 * 10000
= 7850
P (Z < .79)
Mean 0
Standard deviation 1
e. Ranking
Expected rank = P(Z < .79) * 10000
= .785 * 10000
= 7850
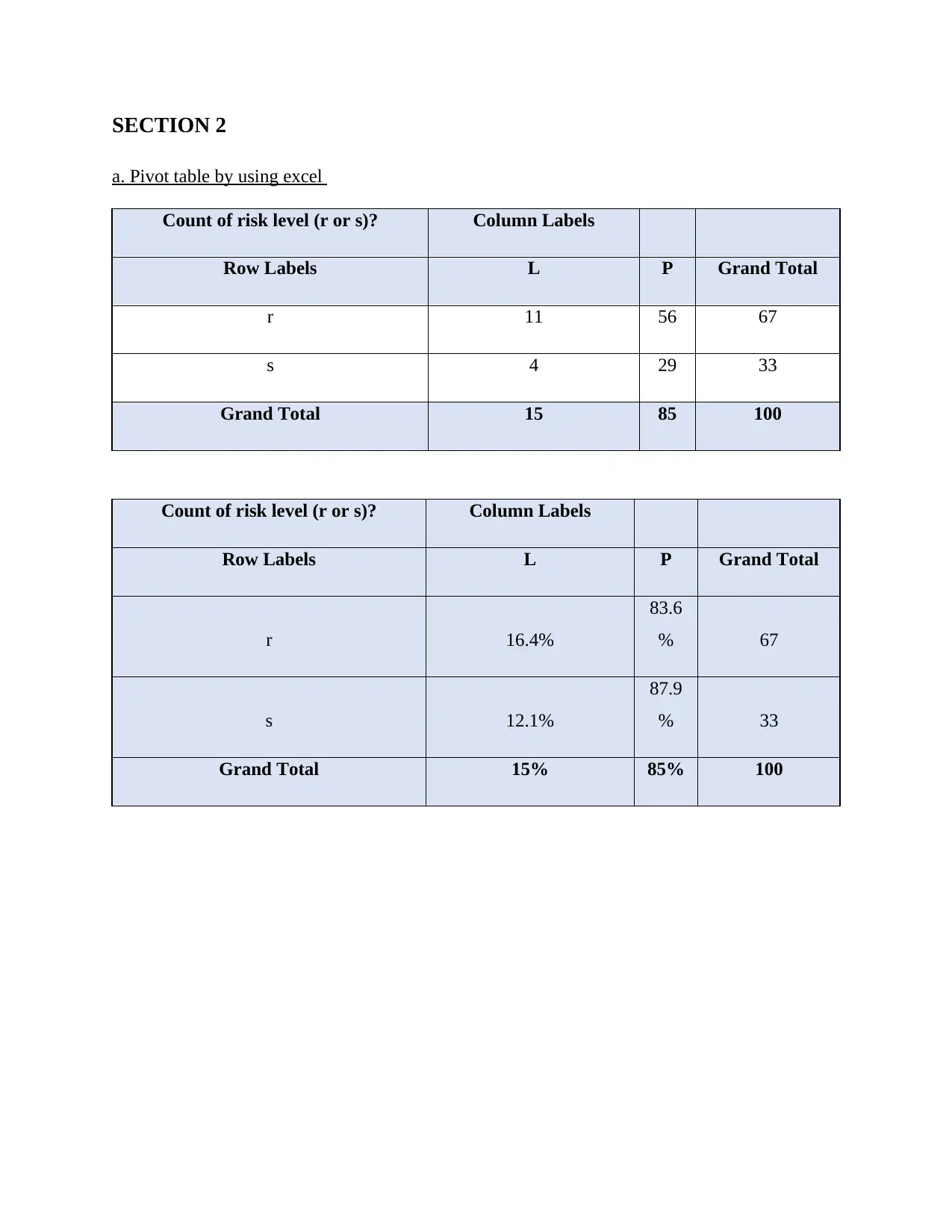
SECTION 2
a. Pivot table by using excel
Count of risk level (r or s)? Column Labels
Row Labels L P Grand Total
r 11 56 67
s 4 29 33
Grand Total 15 85 100
Count of risk level (r or s)? Column Labels
Row Labels L P Grand Total
r 16.4%
83.6
% 67
s 12.1%
87.9
% 33
Grand Total 15% 85% 100
a. Pivot table by using excel
Count of risk level (r or s)? Column Labels
Row Labels L P Grand Total
r 11 56 67
s 4 29 33
Grand Total 15 85 100
Count of risk level (r or s)? Column Labels
Row Labels L P Grand Total
r 16.4%
83.6
% 67
s 12.1%
87.9
% 33
Grand Total 15% 85% 100
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
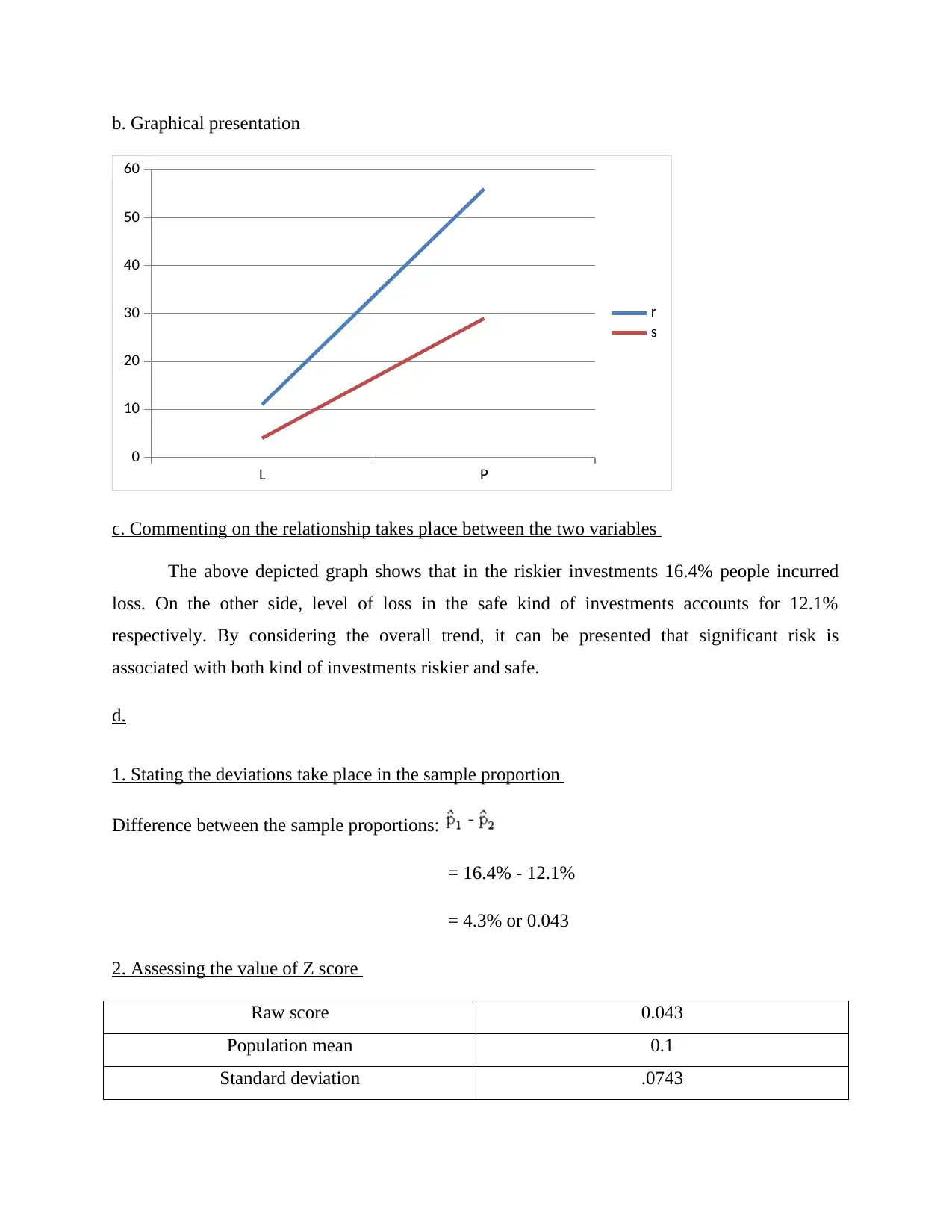
b. Graphical presentation
L P
0
10
20
30
40
50
60
r
s
c. Commenting on the relationship takes place between the two variables
The above depicted graph shows that in the riskier investments 16.4% people incurred
loss. On the other side, level of loss in the safe kind of investments accounts for 12.1%
respectively. By considering the overall trend, it can be presented that significant risk is
associated with both kind of investments riskier and safe.
d.
1. Stating the deviations take place in the sample proportion
Difference between the sample proportions:
= 16.4% - 12.1%
= 4.3% or 0.043
2. Assessing the value of Z score
Raw score 0.043
Population mean 0.1
Standard deviation .0743
L P
0
10
20
30
40
50
60
r
s
c. Commenting on the relationship takes place between the two variables
The above depicted graph shows that in the riskier investments 16.4% people incurred
loss. On the other side, level of loss in the safe kind of investments accounts for 12.1%
respectively. By considering the overall trend, it can be presented that significant risk is
associated with both kind of investments riskier and safe.
d.
1. Stating the deviations take place in the sample proportion
Difference between the sample proportions:
= 16.4% - 12.1%
= 4.3% or 0.043
2. Assessing the value of Z score
Raw score 0.043
Population mean 0.1
Standard deviation .0743
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
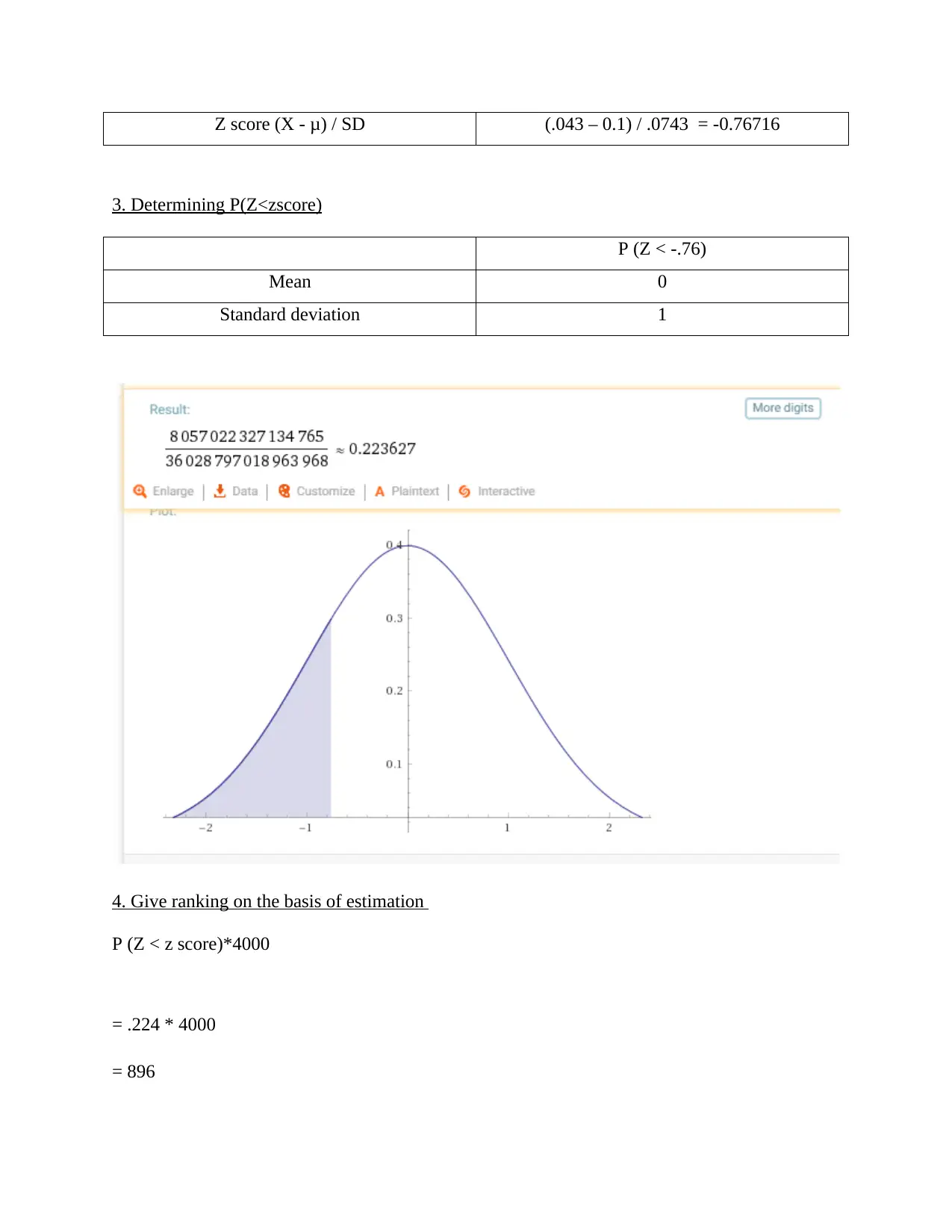
Z score (X - μ) / SD (.043 – 0.1) / .0743 = -0.76716
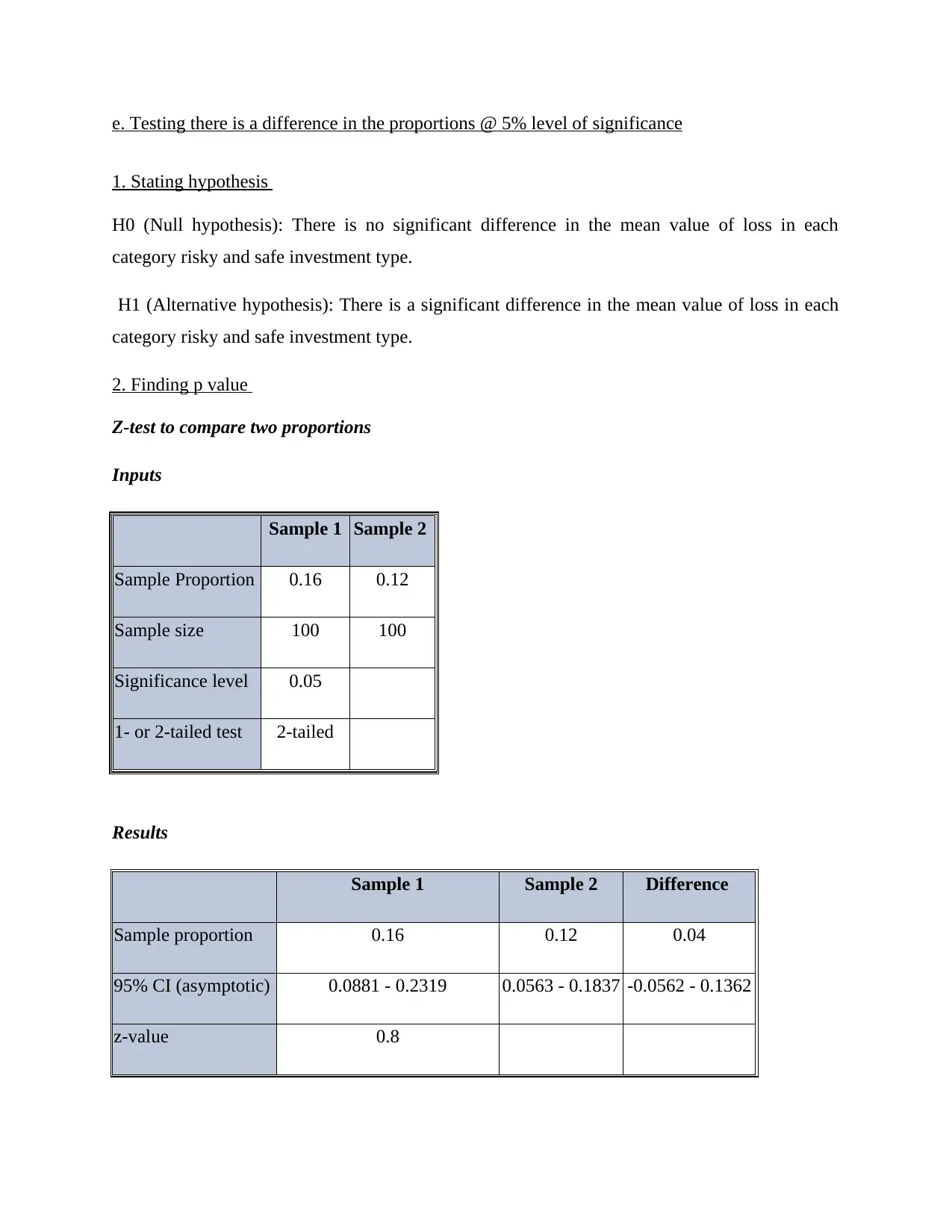
3. Determining P(Z<zscore)
P (Z < -.76)
Mean 0
Standard deviation 1
4. Give ranking on the basis of estimation
P (Z < z score)*4000
= .224 * 4000
= 896
3. Determining P(Z<zscore)
P (Z < -.76)
Mean 0
Standard deviation 1
4. Give ranking on the basis of estimation
P (Z < z score)*4000
= .224 * 4000
= 896
e. Testing there is a difference in the proportions @ 5% level of significance
1. Stating hypothesis
H0 (Null hypothesis): There is no significant difference in the mean value of loss in each
category risky and safe investment type.
H1 (Alternative hypothesis): There is a significant difference in the mean value of loss in each
category risky and safe investment type.
2. Finding p value
Z-test to compare two proportions
Inputs
Sample 1 Sample 2
Sample Proportion 0.16 0.12
Sample size 100 100
Significance level 0.05
1- or 2-tailed test 2-tailed
Results
Sample 1 Sample 2 Difference
Sample proportion 0.16 0.12 0.04
95% CI (asymptotic) 0.0881 - 0.2319 0.0563 - 0.1837 -0.0562 - 0.1362
z-value 0.8
1. Stating hypothesis
H0 (Null hypothesis): There is no significant difference in the mean value of loss in each
category risky and safe investment type.
H1 (Alternative hypothesis): There is a significant difference in the mean value of loss in each
category risky and safe investment type.
2. Finding p value
Z-test to compare two proportions
Inputs
Sample 1 Sample 2
Sample Proportion 0.16 0.12
Sample size 100 100
Significance level 0.05
1- or 2-tailed test 2-tailed
Results
Sample 1 Sample 2 Difference
Sample proportion 0.16 0.12 0.04
95% CI (asymptotic) 0.0881 - 0.2319 0.0563 - 0.1837 -0.0562 - 0.1362
z-value 0.8
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
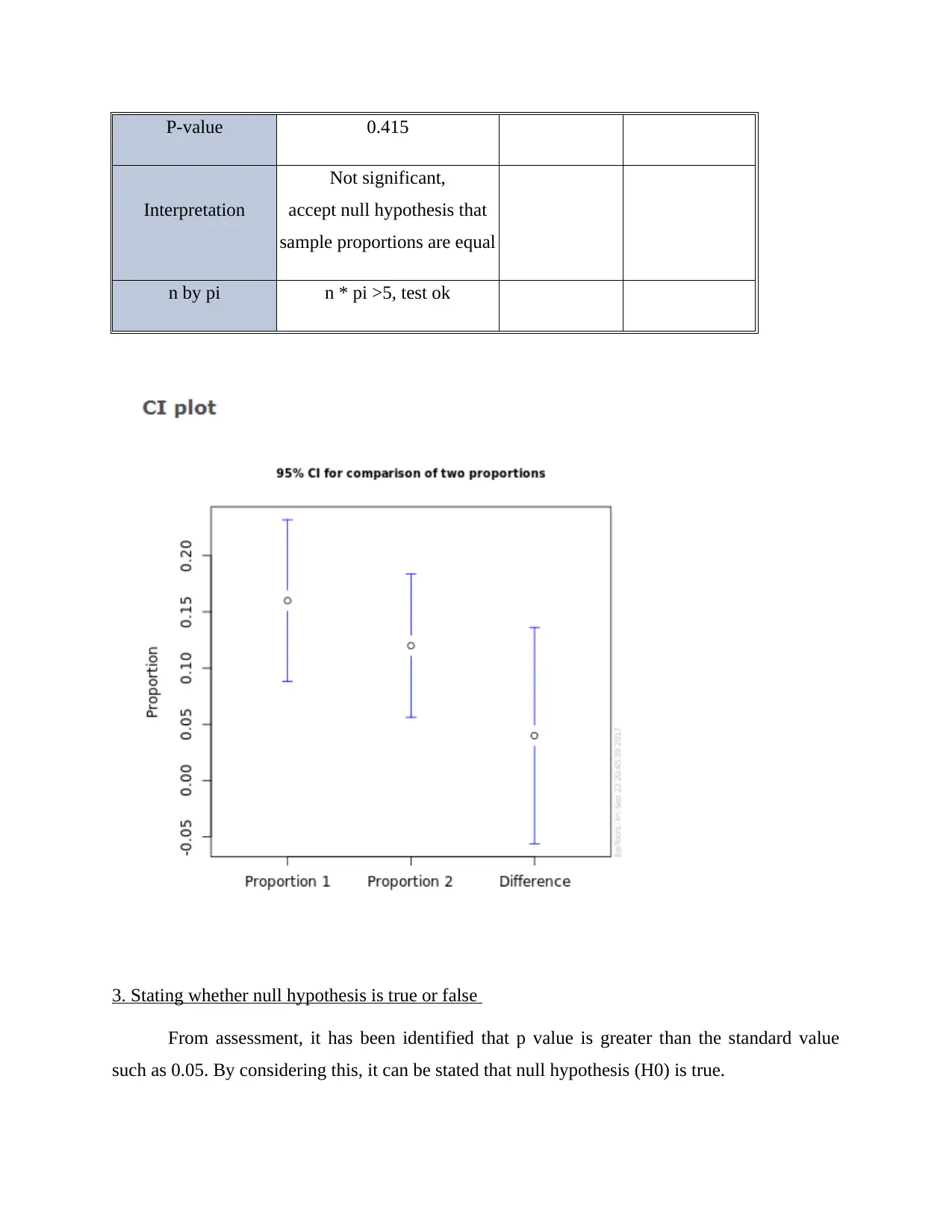
P-value 0.415
Interpretation
Not significant,
accept null hypothesis that
sample proportions are equal
n by pi n * pi >5, test ok
3. Stating whether null hypothesis is true or false
From assessment, it has been identified that p value is greater than the standard value
such as 0.05. By considering this, it can be stated that null hypothesis (H0) is true.
Interpretation
Not significant,
accept null hypothesis that
sample proportions are equal
n by pi n * pi >5, test ok
3. Stating whether null hypothesis is true or false
From assessment, it has been identified that p value is greater than the standard value
such as 0.05. By considering this, it can be stated that null hypothesis (H0) is true.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
4. Conclusion
It can be concluded from the output of statistical analysis that p>0.05 which is turn
shows that mean value of loss is similar in both the cases risky and safe kind of investment.
Thus, it can be stated that investors should invest money in the securities by considering the
market trend and other related factors.
SECTION 3
a. Creating a pivot table for summarizing statistical information
Row Labels Count of High risk Average of return Std-Dev of return
n 74 0.035 0.003
y 26 0.07 0.097
Grand Total 100 0.044 0.051
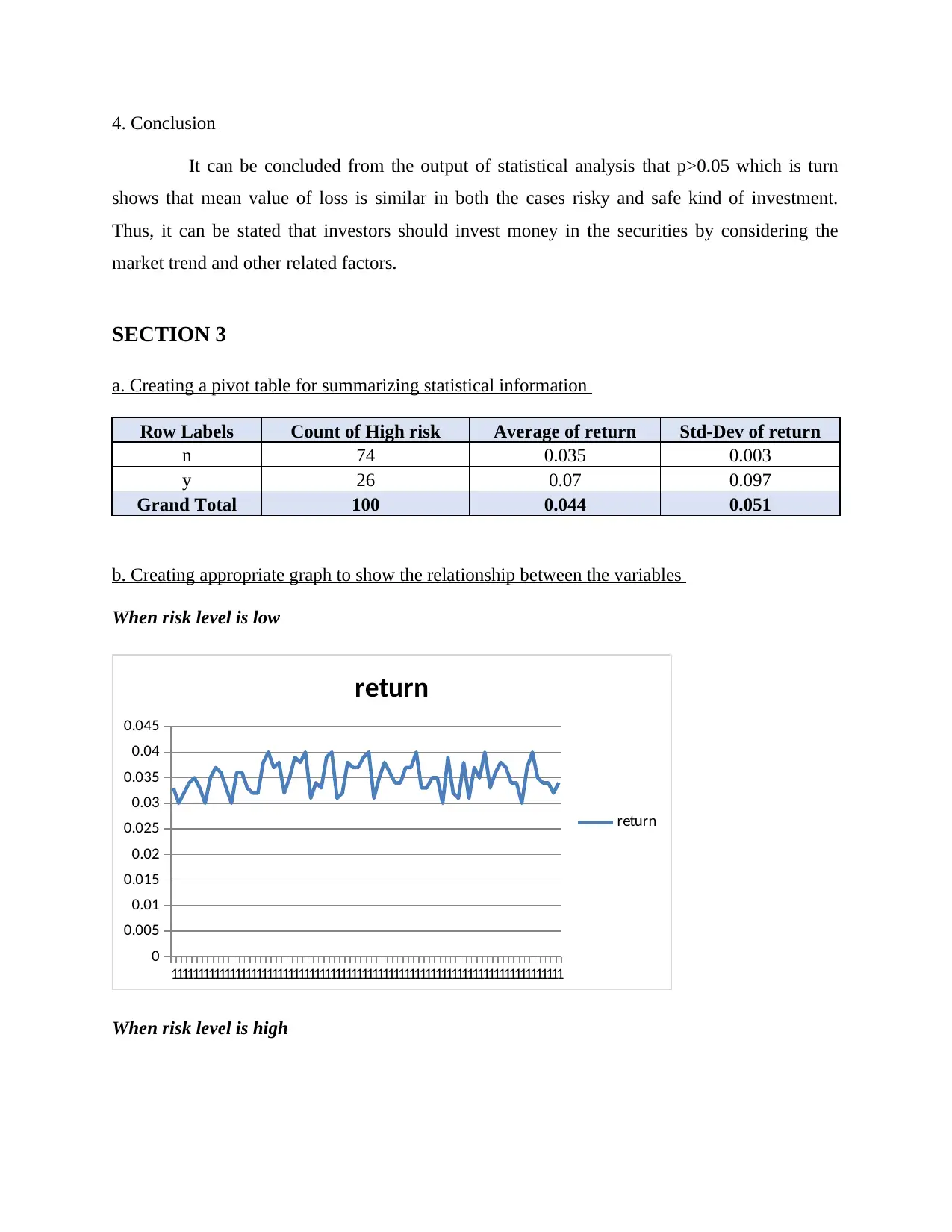
b. Creating appropriate graph to show the relationship between the variables
When risk level is low
11111111111111111111111111111111111111111111111111111111111111111111111111
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
return
return
When risk level is high
It can be concluded from the output of statistical analysis that p>0.05 which is turn
shows that mean value of loss is similar in both the cases risky and safe kind of investment.
Thus, it can be stated that investors should invest money in the securities by considering the
market trend and other related factors.
SECTION 3
a. Creating a pivot table for summarizing statistical information
Row Labels Count of High risk Average of return Std-Dev of return
n 74 0.035 0.003
y 26 0.07 0.097
Grand Total 100 0.044 0.051
b. Creating appropriate graph to show the relationship between the variables
When risk level is low
11111111111111111111111111111111111111111111111111111111111111111111111111
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
return
return
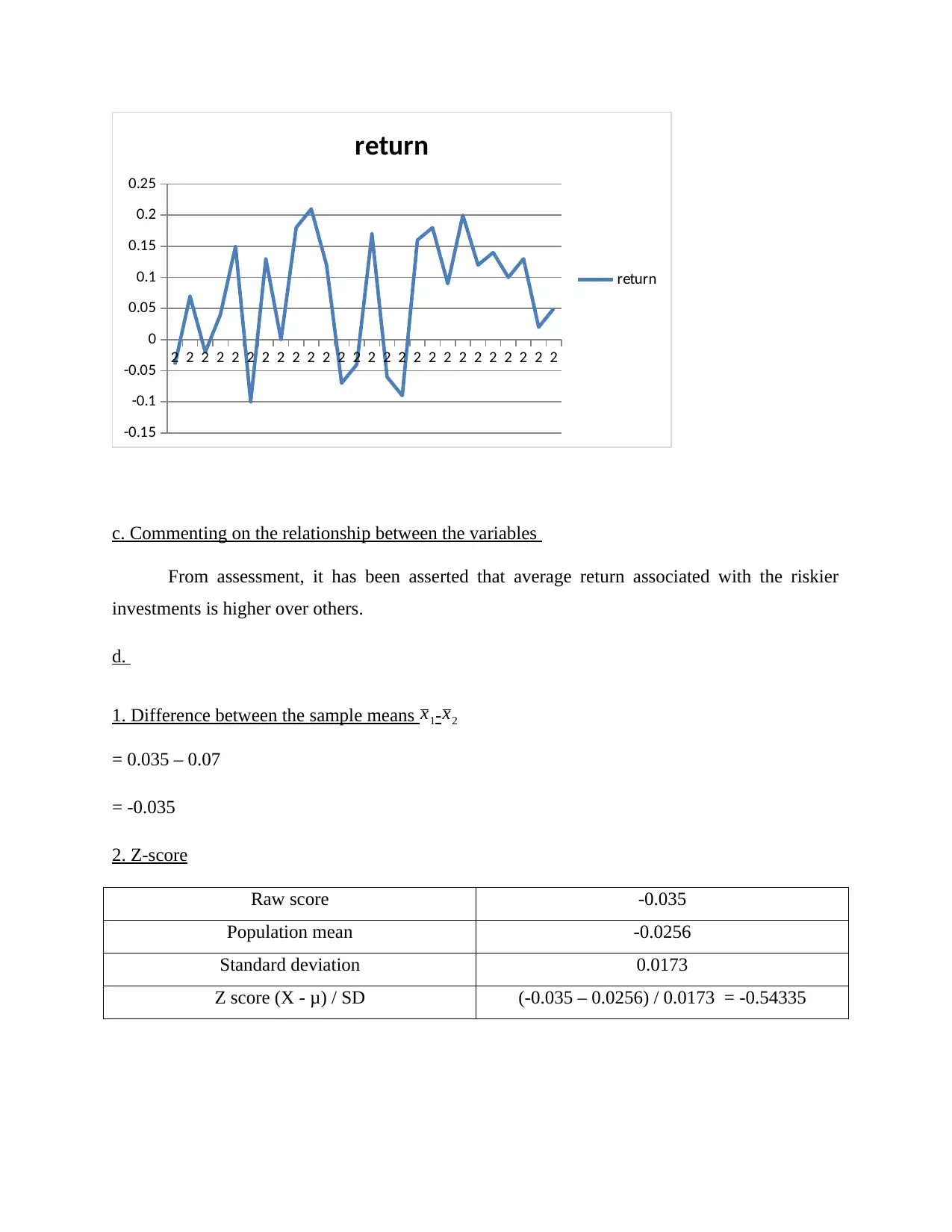
When risk level is high
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
return
return
c. Commenting on the relationship between the variables
From assessment, it has been asserted that average return associated with the riskier
investments is higher over others.
d.
1. Difference between the sample means x1-x2
= 0.035 – 0.07
= -0.035
2. Z-score
Raw score -0.035
Population mean -0.0256
Standard deviation 0.0173
Z score (X - μ) / SD (-0.035 – 0.0256) / 0.0173 = -0.54335
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
return
return
c. Commenting on the relationship between the variables
From assessment, it has been asserted that average return associated with the riskier
investments is higher over others.
d.
1. Difference between the sample means x1-x2
= 0.035 – 0.07
= -0.035
2. Z-score
Raw score -0.035
Population mean -0.0256
Standard deviation 0.0173
Z score (X - μ) / SD (-0.035 – 0.0256) / 0.0173 = -0.54335
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 18
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





