Multiple Linear Regression Analysis 2022

Running Head: Multiple Linear Regression. 1
Application of Multiple Linear Regression to Solve the Big Grocery Management
Problem.
Name
Institution
Date
Professor

Regression Modelling 2
According to Chatterjee and Hadi (2015), the MLR equation can be written as: Y=I0 +
I1X1 + I2X2 + . . .+ InXn + μ where, Y is the dependent variable, I’s are the coefficients, X’s are the
independent variables and μ is the error term.
In the analysis, we need to find the management choice to apply to a new store. This lead
question was affected by three major factors which include; the store size, the location, and the
management. There were 10 locations which were summarized basing on three variables
collected. These outcomes included the revenue, population of customers and the size in square
feet of different business branches. Thus, the idea is to define the dependent and independent
variables (Cox & Roxbee, 2018) and then apply the analysis.
The dependent variable for this analysis was the revenue amount collected from
different locations. The independent variables included: -
 Size – this is the size in square feet of each branch in a different location.
 Population – The number of customers who visit a particular branch
“The good data scientist has thought about these subjective choices and is willing and ready to
answer questions about these decisions.” (Curtis, 2019, p.g.4). To find the relationship that exists
between revenue, size and population, a multiple linear regression becomes the wisest choice.
Sample data for this analysis is shown below (Refer to appendix 1 & 2).
Table 1: Sample Data
Locatio
n Revenue(y)
Size
(sqFt)(x1)
Population(x
2)
Loc1 $23,665,319.22 48720.39 146073
Loc2 $20,066,838.98 40778.72 134878
Loc3 $23,508,691.46 21654.19 225131
Loc4 $11,748,300.32 33344.11 49987
Loc5 $33,450,105.86 116006.4 89939
Loc6 $18,248,754.69 44655.98 53514
Loc7 $10,943,196.86 8549.08 127423
Loc8 $32,934,788.04
157424.4
8 26790
Loc9 $16,821,187.57 63075.32 17092
Loc10 $19,285,241.45 53256.79 86985

Regression Modelling 3
The model equation for this business problem thus can be stipulated by the following
regression equation (James et al., 2013): -
Revenue = I0 + I1(Size) + I2(Population)+ μ.
Results and Interpretation.
The driving force of the question was to find if the size and population, affects the
revenue incurred by Big Grocery. After visualization, the following compound scatter plot
was obtained.
Figure 1: Compound Scatter Plot.
0 50000 100000 150000 200000 250000$0.00
$5,000,000.00
$10,000,000.00
$15,000,000.00
$20,000,000.00
$25,000,000.00
$30,000,000.00
$35,000,000.00
$40,000,000.00
f(x) = 140.30906805577 x + 12824569.3242446
R² = 0.681726997806569
f(x) = 2.49295663311751 x + 20828464.067132
R² = 0.000433753809236048
Compound Scatter Plot
Population Linear (Population)
Linear (Population) Size (sqFt)
Linear (Size (sqFt)) Linear (Size (sqFt))
Size and Population.
Revenue
As clearly depicted, the linear relationship between size and revenue is high compared to
that of Population. This however can be boosted by performing multiple linear regression using
both size and population combined. The assumption will be Revenue depends on both Size and
Population of the grocery store.
With the above model in question, using data analysis tool-pack in excel, the following
output was produced.
Table 2: Regression Statistics.
SUMMARY OUTPUT

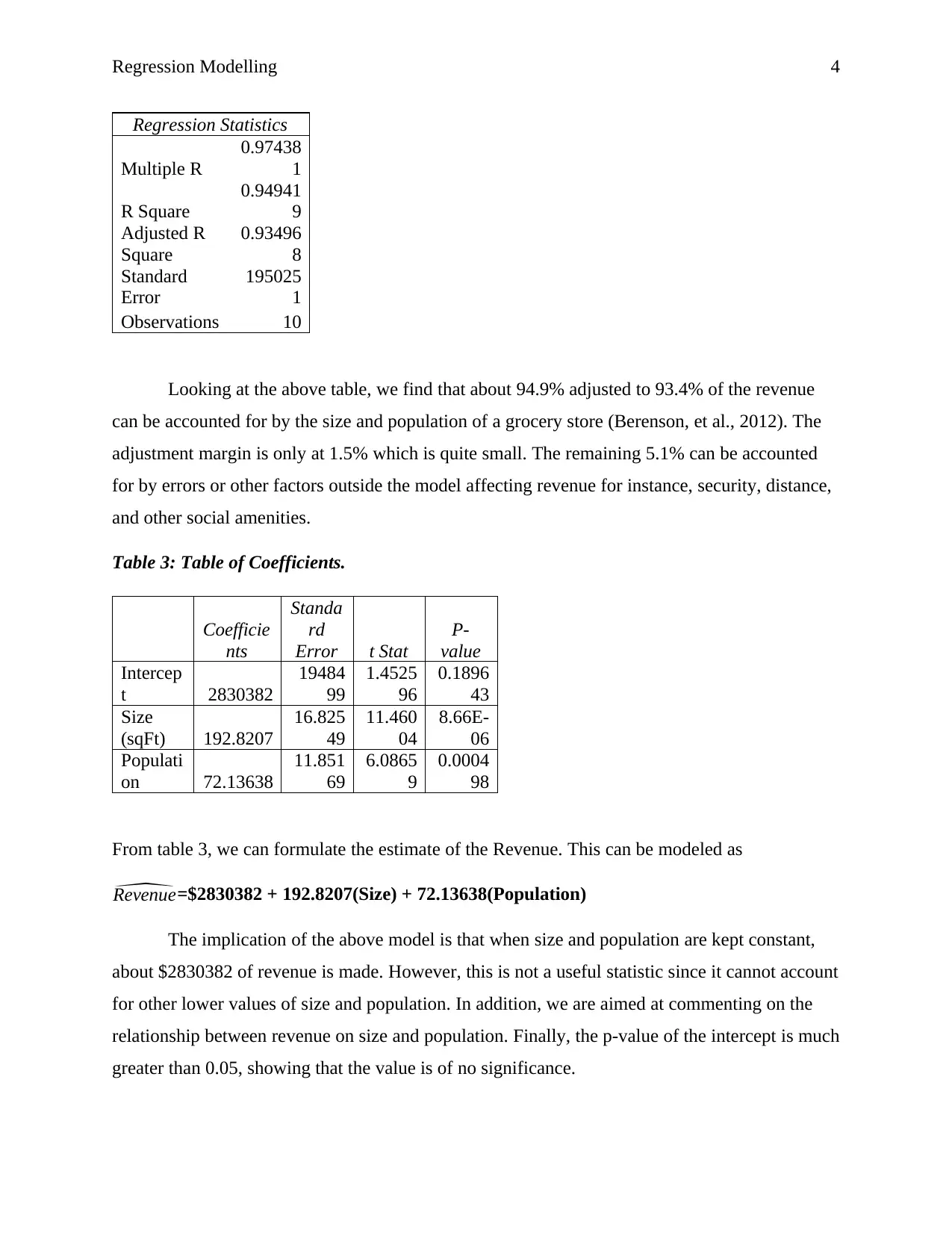
Regression Modelling 4
Regression Statistics
Multiple R
0.97438
1
R Square
0.94941
9
Adjusted R
Square
0.93496
8
Standard
Error
195025
1
Observations 10
Looking at the above table, we find that about 94.9% adjusted to 93.4% of the revenue
can be accounted for by the size and population of a grocery store (Berenson, et al., 2012). The
adjustment margin is only at 1.5% which is quite small. The remaining 5.1% can be accounted
for by errors or other factors outside the model affecting revenue for instance, security, distance,
and other social amenities.
Table 3: Table of Coefficients.
Coefficie
nts
Standa
rd
Error t Stat
P-
value
Intercep
t 2830382
19484
99
1.4525
96
0.1896
43
Size
(sqFt) 192.8207
16.825
49
11.460
04
8.66E-
06
Populati
on 72.13638
11.851
69
6.0865
9
0.0004
98
From table 3, we can formulate the estimate of the Revenue. This can be modeled as
^Revenue=$2830382 + 192.8207(Size) + 72.13638(Population)
The implication of the above model is that when size and population are kept constant,
about $2830382 of revenue is made. However, this is not a useful statistic since it cannot account
for other lower values of size and population. In addition, we are aimed at commenting on the
relationship between revenue on size and population. Finally, the p-value of the intercept is much
greater than 0.05, showing that the value is of no significance.

Regression Modelling 5
The impact of the variables under consideration can be interpreted as follows;
 The coefficient for the size variable is estimated at 192. 82. The implication is that a unit
increase in the square footage of a grocery store would result to a corresponding increase
of revenue by $192.82 This is a positive relationship depicted by the size, which is no
coincidence. Thus, for a business to perform better, the management must possess a vast
amount of square footage. Looking at the significance level depending on the p-value, the
size plays as a highly significant variable (Due to the p-value [8.66E-06] being less than
0.05).
 Further examination on the population, we find out that an increase in population leads to
a resultant increase in revenue by $72.14, holding other factors constant (i.e. at 0). This
variable also plays a big significance role (p-value of 0.000498 being less than 0.05). It,
therefore, makes the statement correct that availability of customers due to the high
population affects positively the revenue incurred by the business.
Underlying Assumptions.
Considering the four principles of regression, we have to subject each condition to the estimates
found.
1. Linear in Parameters.
This attribute is already defined by the scatter plots as shown below. Also looking at the
coefficient of determination, about 94.9% of the revenue can be accounted for by the
independent variables in question. This is an element in ascertaining the goodness of fit (GoF) of
a model (Akter D’Ambra & Ray, 2011).
Figure 2: Scatter Diagram.

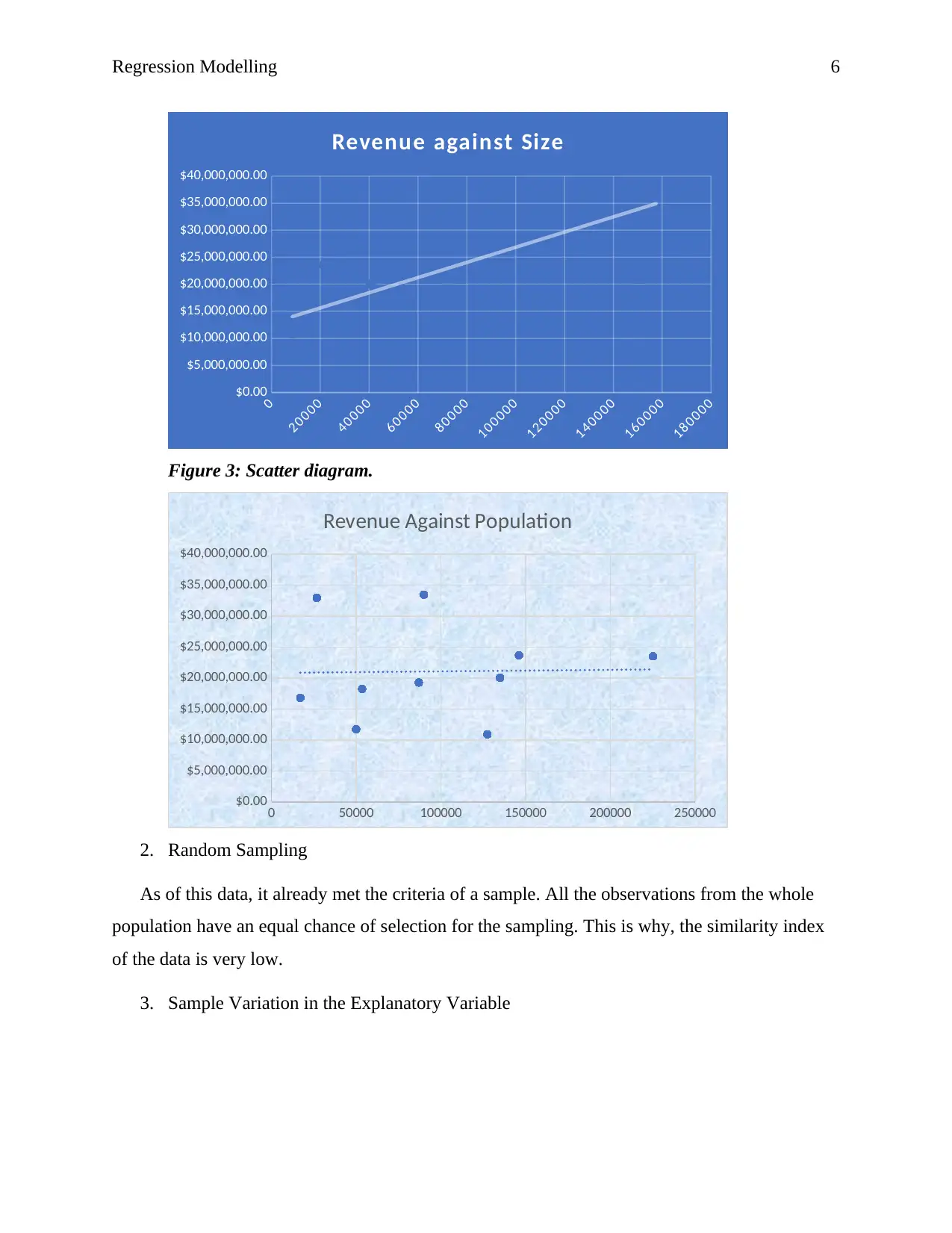
Regression Modelling 6
0
200 0 0
400 0 0
600 0 0
800 0 0
100 0 0 0
120 0 0 0
140 0 0 0
160 0 0 0
180 0 0 0
$0.00
$5,000,000.00
$10,000,000.00
$15,000,000.00
$20,000,000.00
$25,000,000.00
$30,000,000.00
$35,000,000.00
$40,000,000.00
Revenue against Size
Figure 3: Scatter diagram.
0 50000 100000 150000 200000 250000
$0.00
$5,000,000.00
$10,000,000.00
$15,000,000.00
$20,000,000.00
$25,000,000.00
$30,000,000.00
$35,000,000.00
$40,000,000.00
Revenue Against Population
2. Random Sampling
As of this data, it already met the criteria of a sample. All the observations from the whole
population have an equal chance of selection for the sampling. This is why, the similarity index
of the data is very low.
3. Sample Variation in the Explanatory Variable

Regression Modelling 7
For the sake of this analysis, there is an issue that arises due to the small sample that is less
than 30 observations. This creates a problem of power failure, hence the true effect of each of the
variables is lowered (Button et al., 2013). According to Doane and Seward, a good sample size
should be estimated at 30 and above observations. This will always call for simulations in cases
where the real data cannot contain up to the required minimum sample to satisfying the modeling
procedures (Greasley, 2017).
4. Zero Mean of the error term conditional on the independent variables.
This condition only holds if the error term is non-correlated with the independent variables.
For revenue accumulation as a measure of good managerial skill, many factors play handy.
However, we need to avoid the factors having their interaction to remove the correlation between
a factor and the error term (dataminingincae,2014). Looking at this model, we find out that there
is much sense depicted by the variables in question. For instance, it is required that a location
with a higher number of customers will acquire much revenue compared to a low populated area.
Also, a business with big square footage has thus to make more revenue. The error accounted for
here can only be a 5.1% which may also include other factors. The residuals can also be
interpreted to get the new predicted values.
In conclusion, Big Groceries should make the following decision.
Decision: CEO to choose a manager who has abilities to control higher population and a huge
business size.

Regression Modelling 8
References.
Akter, S., D'Ambra, J., & Ray, P. (2011). An evaluation of PLS based complex models: the roles
of power analysis, predictive relevance, and GoF index.
Berenson, M., Levine, D., Szabat, K. A., & Krehbiel, T. C. (2012). Basic business statistics:
Concepts and applications. Pearson higher education AU.
Button, K. S., Ioannidis, J. P., Mokrysz, C., Nosek, B. A., Flint, J., Robinson, E. S., & Munafò,
M. R. (2013). Power failure: why small sample size undermines the reliability of
neuroscience. Nature Reviews Neuroscience, 14(5), 365.
Chatterjee, S., & Hadi, A. S. (2015). Regression analysis by example. John Wiley & Sons.
Cox, David Roxbee. Analysis of binary data. Routledge, 2018.
Dataminingincae. (2014, September 12). Retrieved July 31, 2019, from
https://www.youtube.com/watch?v=9yTui_LoSOc
Doane, D. P., & Seward, L. W. (2011). Applied statistics in business and economics. New York,
NY: McGraw-Hill/Irwin,
Greasley, A. (2017). Simulation modelling for business. Routledge.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical
learning (Vol. 112, p. 18). New York: springer.

Regression Modelling 9
Appendix
1. Histogram depicting revenue.
Loc1 Loc2 Loc3 Loc4 Loc5 Loc6 Loc7 Loc8 Loc9 Loc10
$0.00
$5,000,000.00
$10,000,000.00
$15,000,000.00
$20,000,000.00
$25,000,000.00
$30,000,000.00
$35,000,000.00
$40,000,000.00
$23,665,319.22
$20,066,838.98
$23,508,691.46
$11,748,300.32
$33,450,105.86
$18,248,754.69
$10,943,196.86
$32,934,788.04
$16,821,187.57
$19,285,241.45
Revenue
Revenue
2. Multiple Bar Chart showing size and population.

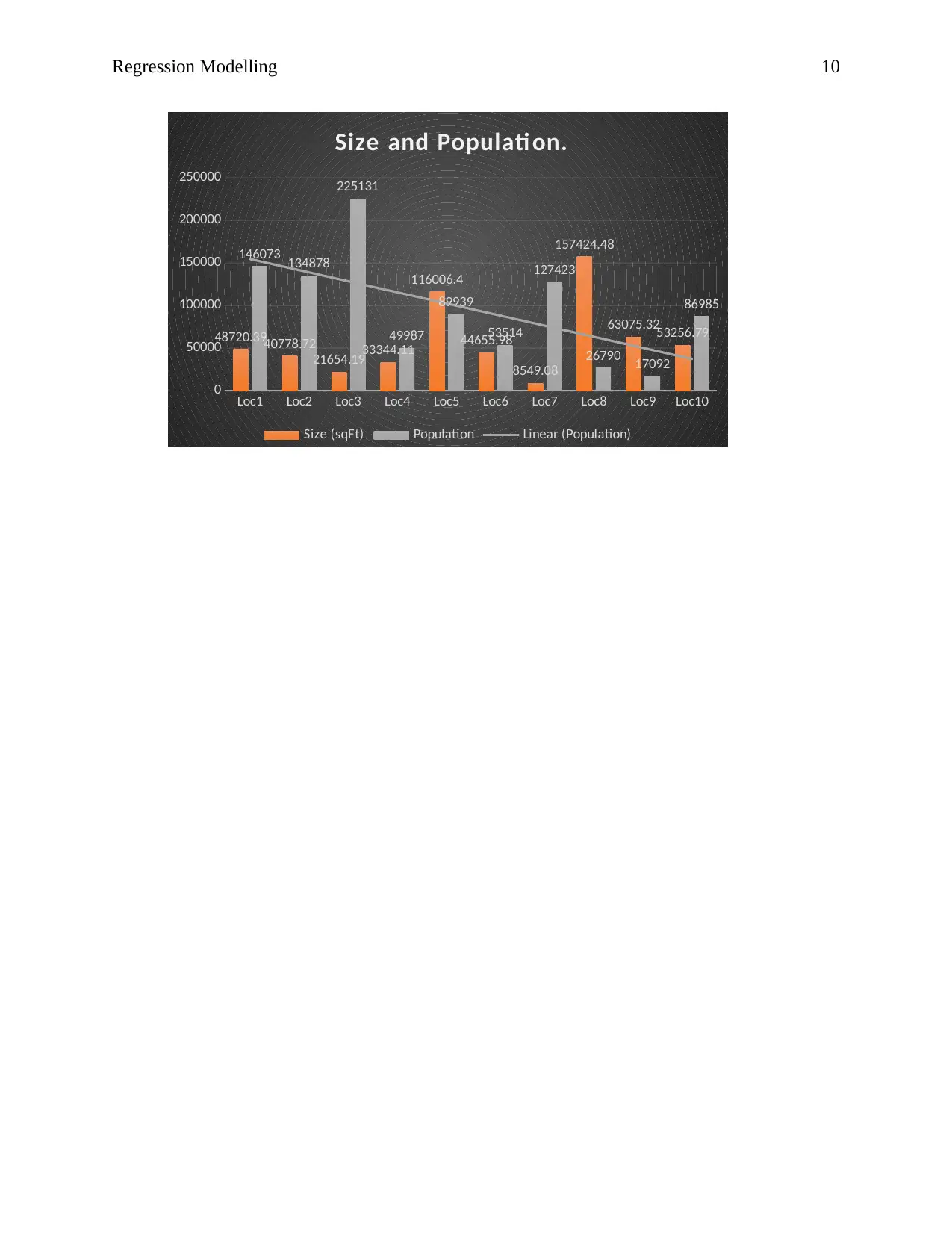
Regression Modelling 10
Loc1 Loc2 Loc3 Loc4 Loc5 Loc6 Loc7 Loc8 Loc9 Loc10
0
50000
100000
150000
200000
250000
48720.3940778.72
21654.19
33344.11
116006.4
44655.98
8549.08
157424.48
63075.32
53256.79
146073 134878
225131
49987
89939
53514
127423
26790 17092
86985
Size and Populati on.
Size (sqFt) Population Linear (Population)