Buffer Solutions and Chemical Equilibrium
VerifiedAdded on 2020/04/21
|11
|1811
|440
AI Summary
This assignment delves into the crucial role of buffer solutions in maintaining pH stability. It presents a table showcasing the pH changes and corresponding buffer capacities as sodium hydroxide (NaOH) is added to a solution. The analysis involves interpreting titration curves and understanding the relationship between buffer capacity and pH. The document emphasizes the significance of buffers in various applications, particularly in medicine where maintaining a constant pH is vital for effective drug function.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Chemistry-Based Practical Report 1
CHEMISTRY BASED PRACTICAL REPORT
By NAME
Course
Professor’s Name
Institution
Location of Institution
Date
CHEMISTRY BASED PRACTICAL REPORT
By NAME
Course
Professor’s Name
Institution
Location of Institution
Date
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Chemistry-Based Practical Report 2
Chemistry-Based Practical Report
The buffer capacity practical that was carried out in this unit is defined as the amount of
moles of acid or base that is required to cause a variation of pH value of one liter of the solution
by one unit. Buffer solutions are capable of maintaining a relatively constant pH value if only a
little amount of acid or base is added and therefore this resistance to variations in pH can also be
defined as buffer capacity (Frederick A. Bettelheim, 2012).
1. pH Definition
pH is an abbreviation for the potential of hydrogen and it is a measure of how much acidic or
alkaline an aqueous solution is (Jorge G. Ibanez, 2011). It is represented by the equation below
pH=-log[H+]
The “p” in pH implies that it is power of 10 since the scale is a logarithmic function and thus
implying that for values that are below 7 on the pH chart, acidity increases by a factor of 10
down the pH chart and for values above 7 on pH chart each value denotes acidity decreases by a
factor of 10 up the pH chart.
2. Dissociation of weak acids
Weak acids do not dissociate fully in solutions thus they do not give all the hydrogen ions to the
solution. Calculation of pH of weak acids needs one to take into account unique ionization
constant (Ka) and equilibrium concentration (Cox, 2013). They are very important in preparing
buffer solutions. Ka is normally very small in weak acids while pKa is always high. Generally,
dissociation is represented as shown in the equation below;
HA(aq)⇌H+(aq)+A-(aq)
Chemistry-Based Practical Report
The buffer capacity practical that was carried out in this unit is defined as the amount of
moles of acid or base that is required to cause a variation of pH value of one liter of the solution
by one unit. Buffer solutions are capable of maintaining a relatively constant pH value if only a
little amount of acid or base is added and therefore this resistance to variations in pH can also be
defined as buffer capacity (Frederick A. Bettelheim, 2012).
1. pH Definition
pH is an abbreviation for the potential of hydrogen and it is a measure of how much acidic or
alkaline an aqueous solution is (Jorge G. Ibanez, 2011). It is represented by the equation below
pH=-log[H+]
The “p” in pH implies that it is power of 10 since the scale is a logarithmic function and thus
implying that for values that are below 7 on the pH chart, acidity increases by a factor of 10
down the pH chart and for values above 7 on pH chart each value denotes acidity decreases by a
factor of 10 up the pH chart.
2. Dissociation of weak acids
Weak acids do not dissociate fully in solutions thus they do not give all the hydrogen ions to the
solution. Calculation of pH of weak acids needs one to take into account unique ionization
constant (Ka) and equilibrium concentration (Cox, 2013). They are very important in preparing
buffer solutions. Ka is normally very small in weak acids while pKa is always high. Generally,
dissociation is represented as shown in the equation below;
HA(aq)⇌H+(aq)+A-(aq)

Chemistry-Based Practical Report 3
Where HA is the species to be dissociated while A- is the acid conjugate.
The above equation shows that dissociation is reversible.
Ka can be expressed as shown in the equation below
Ka =[ A ‾ ] ¿ ¿
Ka from the above equation shows the ease with which an acid releases its proton and it can also
be noted how dissociation of weak acids change with respect to the H+ level in the solution.
pKa which is used as an index to represent the acidity of weak acids can be defined by the
equation below
pKa =-logKa
3. Preparing pH Buffered Solution
A pH buffered solution is made by adding a base or an acid to a known volume of salt solution.
Normally a strong acid or a strong base is added to a salt whose concentration is known (Steven
S. Zumdahi, 2010). The salt is assumed to be neutral thus able to maintain a constant pH value
and the addition of base or acid may not cause a change in the pH unless the salt solution is
completely reacted on after which the pH value may rise or fall drastically.
4. Acid-Base Titration Generic Principles
Acid-Base titration aids in the determining the unknown concentration of an acid when it is
neutralized by a known concentration of base and vice-versa. The neutralization leads to the
production of a salt and water (Kenkel, 2013). Normally a color indicator is applied to the titer
normally in a flask before starting the titration process for ease of identifying when the point of
neutralization is nearing. In titration, neutralization is achieved at a pH of 7 and at that point the
Where HA is the species to be dissociated while A- is the acid conjugate.
The above equation shows that dissociation is reversible.
Ka can be expressed as shown in the equation below
Ka =[ A ‾ ] ¿ ¿
Ka from the above equation shows the ease with which an acid releases its proton and it can also
be noted how dissociation of weak acids change with respect to the H+ level in the solution.
pKa which is used as an index to represent the acidity of weak acids can be defined by the
equation below
pKa =-logKa
3. Preparing pH Buffered Solution
A pH buffered solution is made by adding a base or an acid to a known volume of salt solution.
Normally a strong acid or a strong base is added to a salt whose concentration is known (Steven
S. Zumdahi, 2010). The salt is assumed to be neutral thus able to maintain a constant pH value
and the addition of base or acid may not cause a change in the pH unless the salt solution is
completely reacted on after which the pH value may rise or fall drastically.
4. Acid-Base Titration Generic Principles
Acid-Base titration aids in the determining the unknown concentration of an acid when it is
neutralized by a known concentration of base and vice-versa. The neutralization leads to the
production of a salt and water (Kenkel, 2013). Normally a color indicator is applied to the titer
normally in a flask before starting the titration process for ease of identifying when the point of
neutralization is nearing. In titration, neutralization is achieved at a pH of 7 and at that point the

Chemistry-Based Practical Report 4
solution is said to be at equilibrium and always accompanied by the production of water and a
salt. An example can be as shown in the equation below
H2SO4(aq)+2NaOH(aq)→Na2SO4(s)+2H2O(l)
5. Buffer Capacity
This refers to the number of moles of an acid or a base that can initiate a variation in pH value of
one liter of the solution by a unit. It gives an indication of a solutions ability to resist a variation
in pH by consuming hydrogen or hydroxyl ions (Tosh, 2013). It is denoted by β and
mathematically represented as
β= ∆ B
∆ pH
Where ∆B =quantity of strong acid or strong base per gram that can change the pH value of 1L
of buffer solution and
∆pH =variation in pH due to the addition of a base or an acid.
6. Maximum Buffering Capacity
As one adds a strong acid or a strong base to a buffered solution, there is a drastic change of pH
up to a point when the concentration of basic components equals the concentration of acidic
components. Buffer solution exhibit optimum buffering capacity when pH=pKa, a point at which
the buffer solution is capable of resisting drastic variations in the value of pH in response to the
addition of acid or base (Philip Denton, 2013). According to Henderson-Hasselbach equation
pH=pKa + log ( [ A ‾ ]
[ HA ]) but since pH=pKa,
solution is said to be at equilibrium and always accompanied by the production of water and a
salt. An example can be as shown in the equation below
H2SO4(aq)+2NaOH(aq)→Na2SO4(s)+2H2O(l)
5. Buffer Capacity
This refers to the number of moles of an acid or a base that can initiate a variation in pH value of
one liter of the solution by a unit. It gives an indication of a solutions ability to resist a variation
in pH by consuming hydrogen or hydroxyl ions (Tosh, 2013). It is denoted by β and
mathematically represented as
β= ∆ B
∆ pH
Where ∆B =quantity of strong acid or strong base per gram that can change the pH value of 1L
of buffer solution and
∆pH =variation in pH due to the addition of a base or an acid.
6. Maximum Buffering Capacity
As one adds a strong acid or a strong base to a buffered solution, there is a drastic change of pH
up to a point when the concentration of basic components equals the concentration of acidic
components. Buffer solution exhibit optimum buffering capacity when pH=pKa, a point at which
the buffer solution is capable of resisting drastic variations in the value of pH in response to the
addition of acid or base (Philip Denton, 2013). According to Henderson-Hasselbach equation
pH=pKa + log ( [ A ‾ ]
[ HA ]) but since pH=pKa,
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Chemistry-Based Practical Report 5
log¿)=0 and thus [ A ‾]
[ HA ]=1 which implies that the solution is at equilibrium.
7. Phosphate Buffer
The dominant buffering components in phosphate buffer are di-hydrogen phosphate ions that
donate hydrogen ions thus acting as the acid and ions of hydrogen phosphate that accepts
hydrogen ions thus acting as the base. The two ions are in equilibrium with one another at a pH
of 7 (Atlas, 2010). At this particular pH, the value of pKa is around 7.21 which is close to the pH
value of 7. Phosphate buffer maintains the pH at a value near pKa value.
8. Autoionization of Water
Pure water can operate as both acids and bases where one water molecule accepts hydrogen ions
from another water molecule thus forming hydronium ion and hydroxide ions respectively
(David W. Oxtoby, 2011). The reaction between the water molecules is at equilibrium and
therefore reversible as expressed below
H2O(l) + H2O(l) ⇌ H3O⁺(aq) + OH‾(aq)
Because water is a neutral solution its pOH is 7 and its pH is 7 thus pOH + pH=14. Also at 25°C
pH+pOH=pKw but Kw=1.0 × 10-14 taking the negative logarithm of Kw, that is to say, pKw =-low.
Thus pKw=14 implying that pOH+pH=14
Also at a temperature of 25°C, the concentration of [OH-] is 1.00×10‾7 M. Since pOH =-log
[OH‾] and pOH=7 for pure water, calculating the antilog of pOH gives the concentration of
hydroxide ions.
9. Strong Base
log¿)=0 and thus [ A ‾]
[ HA ]=1 which implies that the solution is at equilibrium.
7. Phosphate Buffer
The dominant buffering components in phosphate buffer are di-hydrogen phosphate ions that
donate hydrogen ions thus acting as the acid and ions of hydrogen phosphate that accepts
hydrogen ions thus acting as the base. The two ions are in equilibrium with one another at a pH
of 7 (Atlas, 2010). At this particular pH, the value of pKa is around 7.21 which is close to the pH
value of 7. Phosphate buffer maintains the pH at a value near pKa value.
8. Autoionization of Water
Pure water can operate as both acids and bases where one water molecule accepts hydrogen ions
from another water molecule thus forming hydronium ion and hydroxide ions respectively
(David W. Oxtoby, 2011). The reaction between the water molecules is at equilibrium and
therefore reversible as expressed below
H2O(l) + H2O(l) ⇌ H3O⁺(aq) + OH‾(aq)
Because water is a neutral solution its pOH is 7 and its pH is 7 thus pOH + pH=14. Also at 25°C
pH+pOH=pKw but Kw=1.0 × 10-14 taking the negative logarithm of Kw, that is to say, pKw =-low.
Thus pKw=14 implying that pOH+pH=14
Also at a temperature of 25°C, the concentration of [OH-] is 1.00×10‾7 M. Since pOH =-log
[OH‾] and pOH=7 for pure water, calculating the antilog of pOH gives the concentration of
hydroxide ions.
9. Strong Base
Chemistry-Based Practical Report 6
These are bases that dissociate fully in an aqueous solution to produce one or more hydroxide
ions in every molecule of the base. They have very high pH values nearing 14 and they can be
very corrosive.
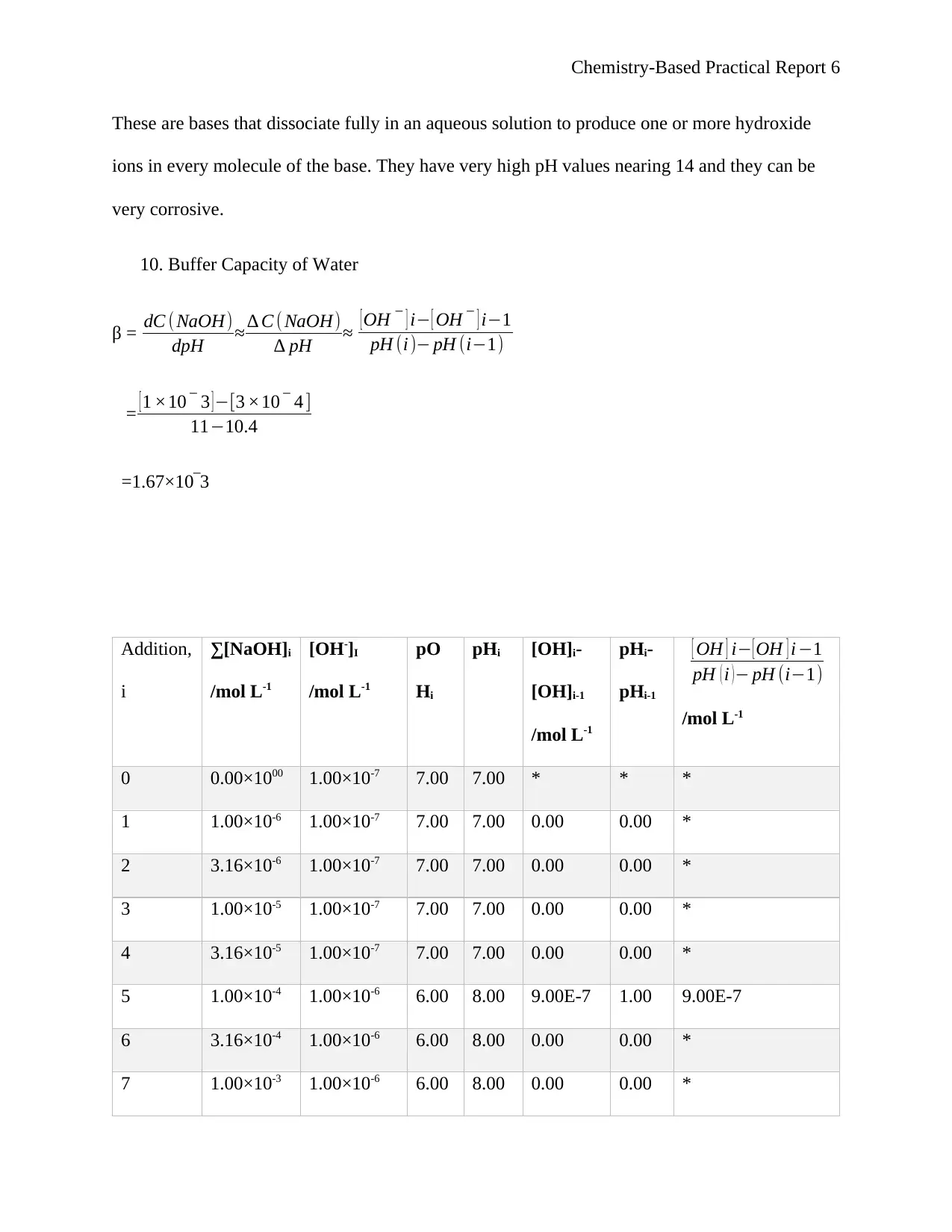
10. Buffer Capacity of Water
β = dC (NaOH)
dpH ≈ ∆ C ( NaOH)
∆ pH ≈ [OH ‾ ] i− [ OH ‾ ] i−1
pH (i )− pH (i−1)
= [1 ×10 ‾ 3 ]−[3 ×10 ‾ 4 ]
11−10.4
=1.67×10‾3
Addition,
i
∑[NaOH]i
/mol L-1
[OH-]I
/mol L-1
pO
Hi
pHi [OH]i-
[OH]i-1
/mol L-1
pHi-
pHi-1
[ OH ] i− [ OH ] i −1
pH ( i ) − pH (i−1)
/mol L-1
0 0.00×1000 1.00×10-7 7.00 7.00 * * *
1 1.00×10-6 1.00×10-7 7.00 7.00 0.00 0.00 *
2 3.16×10-6 1.00×10-7 7.00 7.00 0.00 0.00 *
3 1.00×10-5 1.00×10-7 7.00 7.00 0.00 0.00 *
4 3.16×10-5 1.00×10-7 7.00 7.00 0.00 0.00 *
5 1.00×10-4 1.00×10-6 6.00 8.00 9.00E-7 1.00 9.00E-7
6 3.16×10-4 1.00×10-6 6.00 8.00 0.00 0.00 *
7 1.00×10-3 1.00×10-6 6.00 8.00 0.00 0.00 *
These are bases that dissociate fully in an aqueous solution to produce one or more hydroxide
ions in every molecule of the base. They have very high pH values nearing 14 and they can be
very corrosive.
10. Buffer Capacity of Water
β = dC (NaOH)
dpH ≈ ∆ C ( NaOH)
∆ pH ≈ [OH ‾ ] i− [ OH ‾ ] i−1
pH (i )− pH (i−1)
= [1 ×10 ‾ 3 ]−[3 ×10 ‾ 4 ]
11−10.4
=1.67×10‾3
Addition,
i
∑[NaOH]i
/mol L-1
[OH-]I
/mol L-1
pO
Hi
pHi [OH]i-
[OH]i-1
/mol L-1
pHi-
pHi-1
[ OH ] i− [ OH ] i −1
pH ( i ) − pH (i−1)
/mol L-1
0 0.00×1000 1.00×10-7 7.00 7.00 * * *
1 1.00×10-6 1.00×10-7 7.00 7.00 0.00 0.00 *
2 3.16×10-6 1.00×10-7 7.00 7.00 0.00 0.00 *
3 1.00×10-5 1.00×10-7 7.00 7.00 0.00 0.00 *
4 3.16×10-5 1.00×10-7 7.00 7.00 0.00 0.00 *
5 1.00×10-4 1.00×10-6 6.00 8.00 9.00E-7 1.00 9.00E-7
6 3.16×10-4 1.00×10-6 6.00 8.00 0.00 0.00 *
7 1.00×10-3 1.00×10-6 6.00 8.00 0.00 0.00 *
Chemistry-Based Practical Report 7
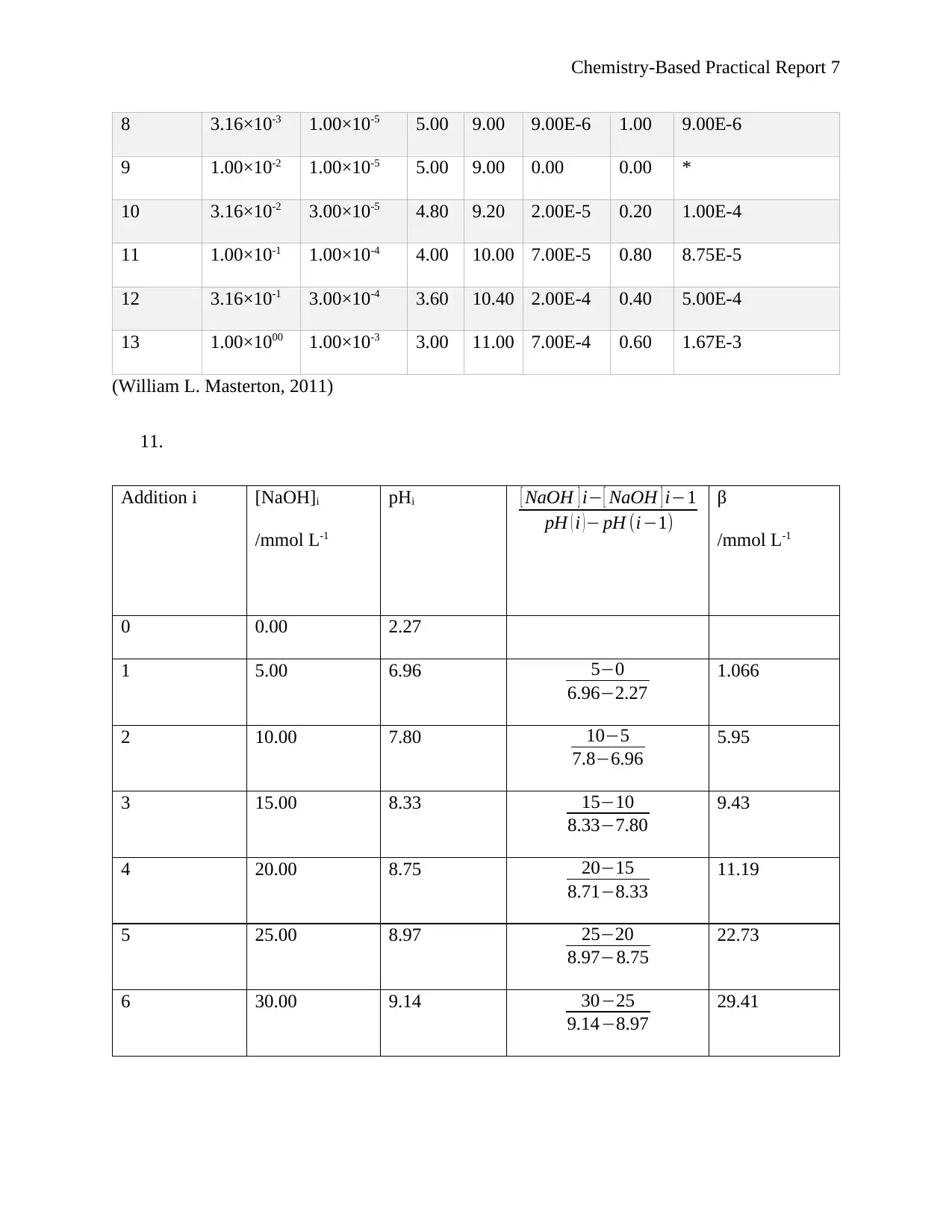
8 3.16×10-3 1.00×10-5 5.00 9.00 9.00E-6 1.00 9.00E-6
9 1.00×10-2 1.00×10-5 5.00 9.00 0.00 0.00 *
10 3.16×10-2 3.00×10-5 4.80 9.20 2.00E-5 0.20 1.00E-4
11 1.00×10-1 1.00×10-4 4.00 10.00 7.00E-5 0.80 8.75E-5
12 3.16×10-1 3.00×10-4 3.60 10.40 2.00E-4 0.40 5.00E-4
13 1.00×1000 1.00×10-3 3.00 11.00 7.00E-4 0.60 1.67E-3
(William L. Masterton, 2011)
11.
Addition i [NaOH]i
/mmol L-1
pHi [ NaOH ] i− [ NaOH ] i−1
pH ( i )− pH (i−1)
β
/mmol L-1
0 0.00 2.27
1 5.00 6.96 5−0
6.96−2.27
1.066
2 10.00 7.80 10−5
7.8−6.96
5.95
3 15.00 8.33 15−10
8.33−7.80
9.43
4 20.00 8.75 20−15
8.71−8.33
11.19
5 25.00 8.97 25−20
8.97−8.75
22.73
6 30.00 9.14 30−25
9.14−8.97
29.41
8 3.16×10-3 1.00×10-5 5.00 9.00 9.00E-6 1.00 9.00E-6
9 1.00×10-2 1.00×10-5 5.00 9.00 0.00 0.00 *
10 3.16×10-2 3.00×10-5 4.80 9.20 2.00E-5 0.20 1.00E-4
11 1.00×10-1 1.00×10-4 4.00 10.00 7.00E-5 0.80 8.75E-5
12 3.16×10-1 3.00×10-4 3.60 10.40 2.00E-4 0.40 5.00E-4
13 1.00×1000 1.00×10-3 3.00 11.00 7.00E-4 0.60 1.67E-3
(William L. Masterton, 2011)
11.
Addition i [NaOH]i
/mmol L-1
pHi [ NaOH ] i− [ NaOH ] i−1
pH ( i )− pH (i−1)
β
/mmol L-1
0 0.00 2.27
1 5.00 6.96 5−0
6.96−2.27
1.066
2 10.00 7.80 10−5
7.8−6.96
5.95
3 15.00 8.33 15−10
8.33−7.80
9.43
4 20.00 8.75 20−15
8.71−8.33
11.19
5 25.00 8.97 25−20
8.97−8.75
22.73
6 30.00 9.14 30−25
9.14−8.97
29.41
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Chemistry-Based Practical Report 8
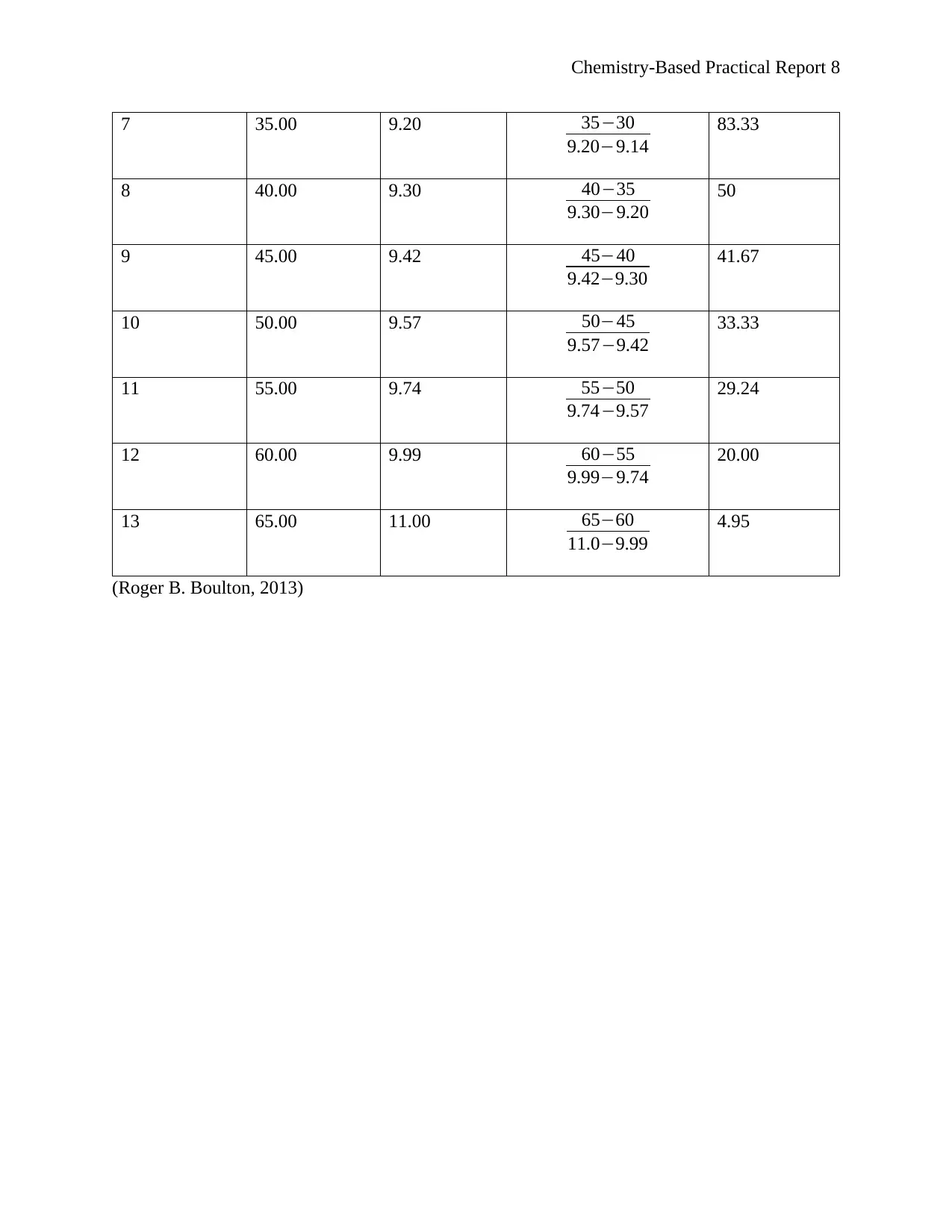
7 35.00 9.20 35−30
9.20−9.14
83.33
8 40.00 9.30 40−35
9.30−9.20
50
9 45.00 9.42 45−40
9.42−9.30
41.67
10 50.00 9.57 50−45
9.57−9.42
33.33
11 55.00 9.74 55−50
9.74−9.57
29.24
12 60.00 9.99 60−55
9.99−9.74
20.00
13 65.00 11.00 65−60
11.0−9.99
4.95
(Roger B. Boulton, 2013)
7 35.00 9.20 35−30
9.20−9.14
83.33
8 40.00 9.30 40−35
9.30−9.20
50
9 45.00 9.42 45−40
9.42−9.30
41.67
10 50.00 9.57 50−45
9.57−9.42
33.33
11 55.00 9.74 55−50
9.74−9.57
29.24
12 60.00 9.99 60−55
9.99−9.74
20.00
13 65.00 11.00 65−60
11.0−9.99
4.95
(Roger B. Boulton, 2013)

Chemistry-Based Practical Report 9
Titration Curve
Titration Curve

Chemistry-Based Practical Report 10
Buffer Capacity Curve
The buffer capacity increases with increase in the concentration of NaOH added up to a
point when a state of equilibrium is achieved at which point the pH is 7. The buffer capacity then
starts reducing as the pH increases towards the maximum pH value of 14.
Buffers help in maintaining the value of pH at a particular value for purposes stability in
aqueous solutions. Medicines are manufactured using aqueous solutions that need their pH to be
kept constant around particular values so that they can work appropriately and effectively
(Crook, 2013). Buffering is thus a very important aspect of chemical equilibrium in very many
chemical reactions.
Buffer Capacity Curve
The buffer capacity increases with increase in the concentration of NaOH added up to a
point when a state of equilibrium is achieved at which point the pH is 7. The buffer capacity then
starts reducing as the pH increases towards the maximum pH value of 14.
Buffers help in maintaining the value of pH at a particular value for purposes stability in
aqueous solutions. Medicines are manufactured using aqueous solutions that need their pH to be
kept constant around particular values so that they can work appropriately and effectively
(Crook, 2013). Buffering is thus a very important aspect of chemical equilibrium in very many
chemical reactions.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Chemistry-Based Practical Report 11
Reference List
Atlas, R. M., 2010. Handbook of Microbiological Media. 4th ed. Paris: CRC Press.
Cox, B. G., 2013. Acids and Bases. 3rd ed. New York: OUP Oxford.
Crook, M. A., 2013. Clinical Biochemistry and Metabolic Medicine. 8th ed. Berlin: CRC Press.
David W. Oxtoby, H. P. G. C., 2011. Principles of Modern Chemistry. 7 ed. Cardiff: Cengage
Learning.
Frederick A. Bettelheim, W. H. B. M. a. C. S. O. F. O. T., 2012. Introduction to General,
Organic and Biochemistry. 10 ed. Chicago: Cengage Learning.
Jorge G. Ibanez, M. H.-E. C. D.-S. A. F.-I. M. M. S., 2011. Environmental Chemistry. illustrated
ed. Rome: Springer Science & Business Media.
Kenkel, J., 2013. Analytical Chemistry for Technicians. 4th ed. London: CRC Press.
Philip Denton, C. R., 2013. Pharmaceutics. Illustrated ed. London: OUP Oxford.
Roger B. Boulton, V. L. S. L. F. B. R. E. K., 2013. Principles and Practices of Winemaking.
Illustrated ed. New Jersey: Springer Science & Business Media.
Steven S. Zumdahi, D. J. D., 2010. Introductory Chemistry. 7th ed. Illinois: Cengage Learning.
Tosh, C., 2013. Advanced Study Guide Chemistry. 1.0 ed. Manchester: Step-by-Step
International Pte. Ltd.
William L. Masterton, C. N. H. E. N., 2011. Chemistry: Principles and Reactions. 7th ed.
Manchester: Cengage Learning.
Reference List
Atlas, R. M., 2010. Handbook of Microbiological Media. 4th ed. Paris: CRC Press.
Cox, B. G., 2013. Acids and Bases. 3rd ed. New York: OUP Oxford.
Crook, M. A., 2013. Clinical Biochemistry and Metabolic Medicine. 8th ed. Berlin: CRC Press.
David W. Oxtoby, H. P. G. C., 2011. Principles of Modern Chemistry. 7 ed. Cardiff: Cengage
Learning.
Frederick A. Bettelheim, W. H. B. M. a. C. S. O. F. O. T., 2012. Introduction to General,
Organic and Biochemistry. 10 ed. Chicago: Cengage Learning.
Jorge G. Ibanez, M. H.-E. C. D.-S. A. F.-I. M. M. S., 2011. Environmental Chemistry. illustrated
ed. Rome: Springer Science & Business Media.
Kenkel, J., 2013. Analytical Chemistry for Technicians. 4th ed. London: CRC Press.
Philip Denton, C. R., 2013. Pharmaceutics. Illustrated ed. London: OUP Oxford.
Roger B. Boulton, V. L. S. L. F. B. R. E. K., 2013. Principles and Practices of Winemaking.
Illustrated ed. New Jersey: Springer Science & Business Media.
Steven S. Zumdahi, D. J. D., 2010. Introductory Chemistry. 7th ed. Illinois: Cengage Learning.
Tosh, C., 2013. Advanced Study Guide Chemistry. 1.0 ed. Manchester: Step-by-Step
International Pte. Ltd.
William L. Masterton, C. N. H. E. N., 2011. Chemistry: Principles and Reactions. 7th ed.
Manchester: Cengage Learning.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





