Comparison of Boeing Company (BA) and General Dynamics (GD) Stock Prices: Analysis and Findings

In this document we will discuss about Comparison of Boeing Company (BA) and General Dynamics (GD) Stock Prices and below are the summary points of this document:- BA's stock price had the highest variability compared to GD and S&P 500. Both BA and GD stocks exhibited left-skewed and normally distributed returns. GD stock had a higher average return compared to BA and showed a less negatively skewed distribution.

1
Comparison between Boeing Company- BA's Stock Price and General
Dynamics- GD's Stock Price
Task B
Answer 1: The returns for the three stocks S&P 500, GD, and BA have been
calculated using Excel for the time period of 01-10-2010 to 01-10-2015. During
return calculations, the transformation
rt = 100*ln ( Pt / Pt-1 )
has been used. The
returns of the three stocks are in percentages, but as instructed no percentage
sign has been used with the return values.
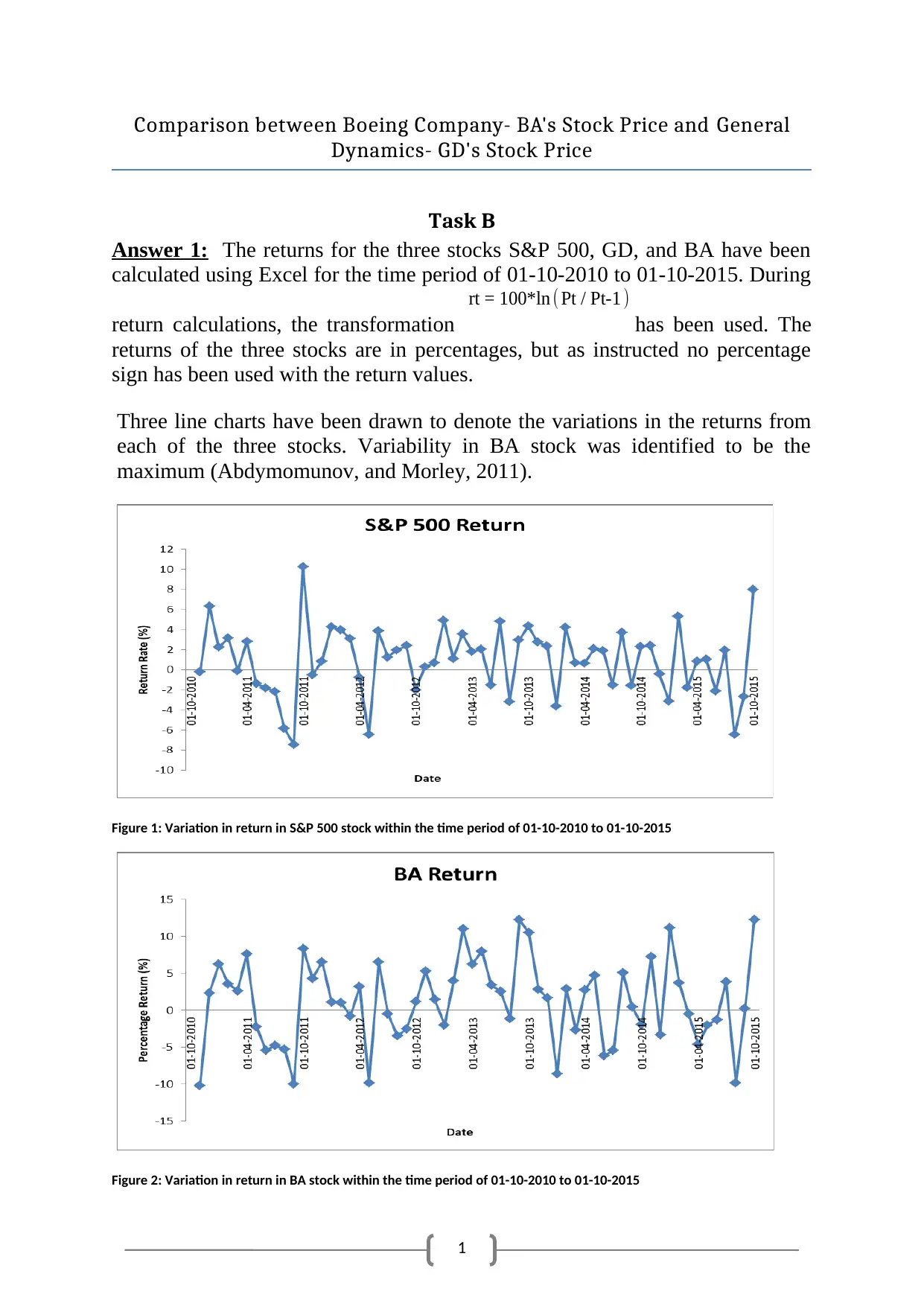
Three line charts have been drawn to denote the variations in the returns from
each of the three stocks. Variability in BA stock was identified to be the
maximum (Abdymomunov, and Morley, 2011).
Figure 1: Variation in return in S&P 500 stock within the time period of 01-10-2010 to 01-10-2015
Figure 2: Variation in return in BA stock within the time period of 01-10-2010 to 01-10-2015

2
Figure 3: Variation in return in GD stock within the time period of 01-10-2010 to 01-10-2015
Jarque-Berra test of normally distributed returns for each of Boeing and
GD
The
Jarque-Berra test of normality has been performed in Excel, where we have
used the formula JB= n
6 ( S2
+
K2
4 )
Where, JB = Jarque-Berra test statistic, n = Sample size, S = skewness of the
series, and K = Excess Kurtosis.
SKEWNESS KURTOSIS n
RETURN_BA -0.127 -0.388 60
RETURN_GD -0.415 0.087 60
JB-Value p-value
Jarque-Berra_BA 10.000 0.054 0.538 0.764
Jarque-Berra_GD 10.000 0.174 1.739 0.419
Jarque-Berra Test
Figure
4: Excel output for JB test for GD and BA returns
From Figure 6 the JB-test statistics for normality of both stocks reveals that
returns of both BA and GD stocks are left skewed and normally distributed. For
BA returns, the p-value (p = 0.764) is greater than α =0 . 05 (5% level of
significance) and reveals that there is no statistical evidence that can reject the
null hypothesis, assuming that the distribution of return of BA stock is normally
distributed. Similarly, distribution of return from GD stock is noted to have no
statistical significance to reject the null hypothesis, establishing the claim that
the distribution of return of BA stock is also normally distributed.

3
Inference about the distribution of the two stock returns series
BA and GD stocks are compared and their distribution patterns have been
graphically evaluated using side-by-side boxplot and histograms. Box and
Whisker plot in Figure 4 clearly illustrates that the average return of GD stock
for the time period of 01-10-2010 to 01-10-2015 is higher compared to BA and
S&P 500. The distribution of the return value of the two stocks GD and BA are
found to be almost normally distributed with a slight negative skewness
(Bratton, and Wachter, 2012).
Figure 5: Side-by-side Boxplot of S&P 500, BA, and GD stocks
Figure 6: Histogram for GD and BA stocks
Interpretation of distribution of returns in GD and BA has been drawn from the
descriptive summary for both of the variables and Figure 4. From Figure 4, it is
apparently noticeable that average return of GD stock is higher than that of BA.
Also, negative skewness is noticed for both the stocks. Figure 5 indicates that
distribution of the rates of GD is less negatively skewed in comparison to the
return of BA stock. The skewness of GD stock is almost zero and the
distribution of returns for GD stock is almost normally distributed. On the other
hand, distribution of the returns of BA stock is comparatively negatively
skewed to GD. Both the distributions with a negative kurtosis value indicated
that the distributions have lighter tails compared to the normal distribution.
The comparative analysis yield that risk-reward profile of GD stock is better
than that of the BA stock, indicating that for an investor GD is a better stock to
invest.

4
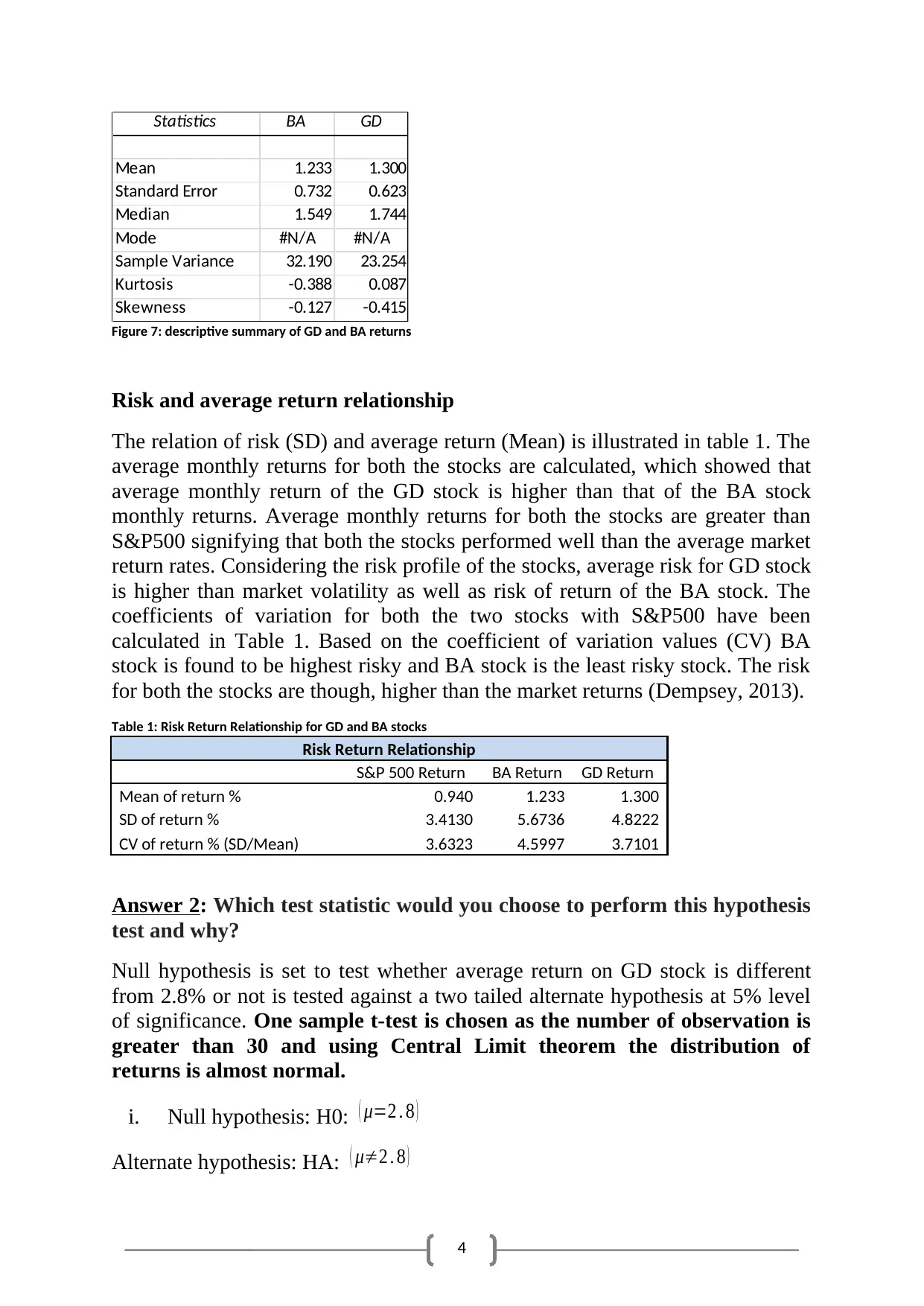
Statistics BA GD
Mean 1.233 1.300
Standard Error 0.732 0.623
Median 1.549 1.744
Mode #N/A #N/A
Sample Variance 32.190 23.254
Kurtosis -0.388 0.087
Skewness -0.127 -0.415
Figure 7: descriptive summary of GD and BA returns
Risk and average return relationship
The relation of risk (SD) and average return (Mean) is illustrated in table 1. The
average monthly returns for both the stocks are calculated, which showed that
average monthly return of the GD stock is higher than that of the BA stock
monthly returns. Average monthly returns for both the stocks are greater than
S&P500 signifying that both the stocks performed well than the average market
return rates. Considering the risk profile of the stocks, average risk for GD stock
is higher than market volatility as well as risk of return of the BA stock. The
coefficients of variation for both the two stocks with S&P500 have been
calculated in Table 1. Based on the coefficient of variation values (CV) BA
stock is found to be highest risky and BA stock is the least risky stock. The risk
for both the stocks are though, higher than the market returns (Dempsey, 2013).
Table 1: Risk Return Relationship for GD and BA stocks
Risk Return Relationship
S&P 500 Return BA Return GD Return
Mean of return % 0.940 1.233 1.300
SD of return % 3.4130 5.6736 4.8222
CV of return % (SD/Mean) 3.6323 4.5997 3.7101
Answer 2: Which test statistic would you choose to perform this hypothesis
test and why?
Null hypothesis is set to test whether average return on GD stock is different
from 2.8% or not is tested against a two tailed alternate hypothesis at 5% level
of significance. One sample t-test is chosen as the number of observation is
greater than 30 and using Central Limit theorem the distribution of
returns is almost normal.
i. Null hypothesis: H0: ( μ=2 . 8 )
Alternate hypothesis: HA: ( μ≠2 . 8 )

5
ii. Confidence level for the test is taken as 95%, and therefore the level of
significance α=0 . 05 or 5% for rejecting the null hypothesis.
iii. The distribution of the test statistic under the null hypothesis:
From the Histogram and Boxplot of GD stock we assume that the
distribution of returns of the stock is normally distributed. Also, the
data is quantitative in nature and number of observation is greater than
30.
iv. The sample-mean X
¿
=1. 3 , standard deviation s=4 . 82 , sample size n=60
Hence, the appropriate test statistic is considered to be t= X
¿
−μ0
s / √ n which is
considered to follow the standard normal distribution N (0, 1).
Calculated value of the test statistic t= X
¿
−μ0
s / √ n = 1 .3−2. 8
4 . 82/ √ 60 =−1 . 5
0 . 62 =−2 . 42
v. At 5% level of significance, tcrit =1. 96 for two tail test and as t cal <t crit the
null hypothesis is rejected at α=0 . 05 .
The excel output for the one sample t-test is provided as below.
Table 2: One Sample t-test for GD stock
t-Test: One-Sample
GD Return
Mean 1.300
Variance 23.254
Observations 60
Hypothesized Mean 2.8
df 59
t Stat -2.410
P(T<=t) one-tail 0.010
t Critical one-tail 1.671
P(T<=t) two-tail 0.019
t Critical two-tail 2.001
The calculated test statistic tcrit falls in the critical or rejection region, and
therefore there is sufficiently strong reason to reject the null hypothesis that
average return of GD stock is equal to 2.8%.
The p-value = P ( t <−tcal ) + P ( t>t cal ) =2∗P ( t <−2 . 42 ) =2∗0 .0093=0 . 0186 < 0.05 =
1.86% implies that there is a 1.86% chance that the average return of GD stock
being 2.8%, and this claim of the null hypothesis is rejected as the probability is
very less than 5%.

6
Answer 3: Any investor will essentially compare and assess the risks associated
with the funds. Here, we compare the risks associated with GD and BA stocks.
Risk of a fund is nothing but the standard deviation of returns for that fund or
stock. To test whether the risks associated with the two stocks are different or
not, and to check whether that difference is statistically significant, we have
used F-test at 5% level of significance. The F-statistics is calculated as
F= s1
2
s2
2
where s1 and s2 are the standard deviations of the monthly returns from GD and
BA stocks (Moder, 2010).
i. Null hypothesis: H0: ( σ1
2=σ2
2 ) is tested against the two tailed Alternate
hypothesis: HA: ( σ1
2≠σ2
2 )
ii. The hypothesis is tested at α = 5% level of significance or 95% level of
confidence.
iii. From the Histogram and Boxplot of GD stock (Figure 5 and Figure 6) we
assume that the distribution is normally distributed. Also, the data is
quantitative in nature and number of observation is greater than 30.
iv. The test statistic calculated value
F= s1
2
s2
2 =32. 190
23 .254 =1 . 384
at
d .o . f =n−1=60−1=59
The critical values are calculated as, F ( 0 .025 , 59 ,59 ) =0 . 5973 and F ( 0 . 975, 59 ,59 ) =1 .674 for
two tailed test at α=0 . 05 .
The calculated F = 1.384 lies in the 95% confidence interval [0.5973, 1.674]
and the p-value is calculated as p=P ( F< 0. 5973 ) + P ( F>1 . 674 ) =0. 2146 >0.05.
v. There is not enough statistical evidence to support the claim that there is a
significant difference in risks of returns of the GD and BA stocks, and
hence the null hypothesis is rejected at 5% level.
The excel output is provided below.
Table 3: F-test for comparison of risks of GD and BA
F-Test Two-Sample for Variances
BA Return GD Return
Mean 1.233 1.300
Variance 32.190 23.254
Observations 60 60
df 59 59
F 1.384
P(F<=f) one-tail 0.107
F Critical one-tail 1.540
F_L 0.5973 F.INV(0.025,59,59)
F_R 1.6741 F.INV(0.975,59,59)
p-value 0.2146 2*F.DIST.RT(G14,G13,H13)

7
Answer 4: To determine whether both GD and BA stocks have the same
population average return, two sample t-test is used.
To test the scenario with the help of t-test statistics it requires that the
distribution of returns from both the stocks should be normally distributed and
independent. The assumption is supported by the low excess kurtosis and near
to zero skewness for both the stocks.
i. Null hypothesis: H0: ( μGD=μBA ) and it is tested against the two tail
alternate hypothesis HA: ( μGD≠μBA )
ii. Level of significance is considered to be α=0 . 05 or 5%.
iii. The t-test statistic for unequal variances is
t = ( X
¿
GD−X
¿
BA ) − ( μGD−μBA )
√ s1
2
n1
+ s2
2
n2 with
d .o . f =115
Here, sample size = 60 > 30, so
t= ( X
¿
GD−X
¿
BA ) − ( μGD−μBA )
√ s1
2
n1
+ s2
2
n2
~ N ( 0,1 )
iv. Now, calculated value of the statistic,
t= ( 1. 3−1 . 233 ) −0
√ 23 . 254
60 +32 . 190
60
=−0 . 069
at d .o . f =115
The critical values of t-statistics are t ( 0 . 025, 115 ) =−1 .981 ∧ t ( 0 .975 , 115 ) =1. 981
The observed or calculated t-value = -0.069 lies in the 95% confidence
interval and it fails to provide any evidence on which we can reject the null
hypothesis.
Also, p-value calculated is P ( t<−tcal ) +P ( t > tcal )=2∗P ( t<−0. 069 ) =0 .945> 0 .05
The excel output for two sample t-test is provided below.
Table 4: Two sample t-test for average return comparison for GD and BA

8
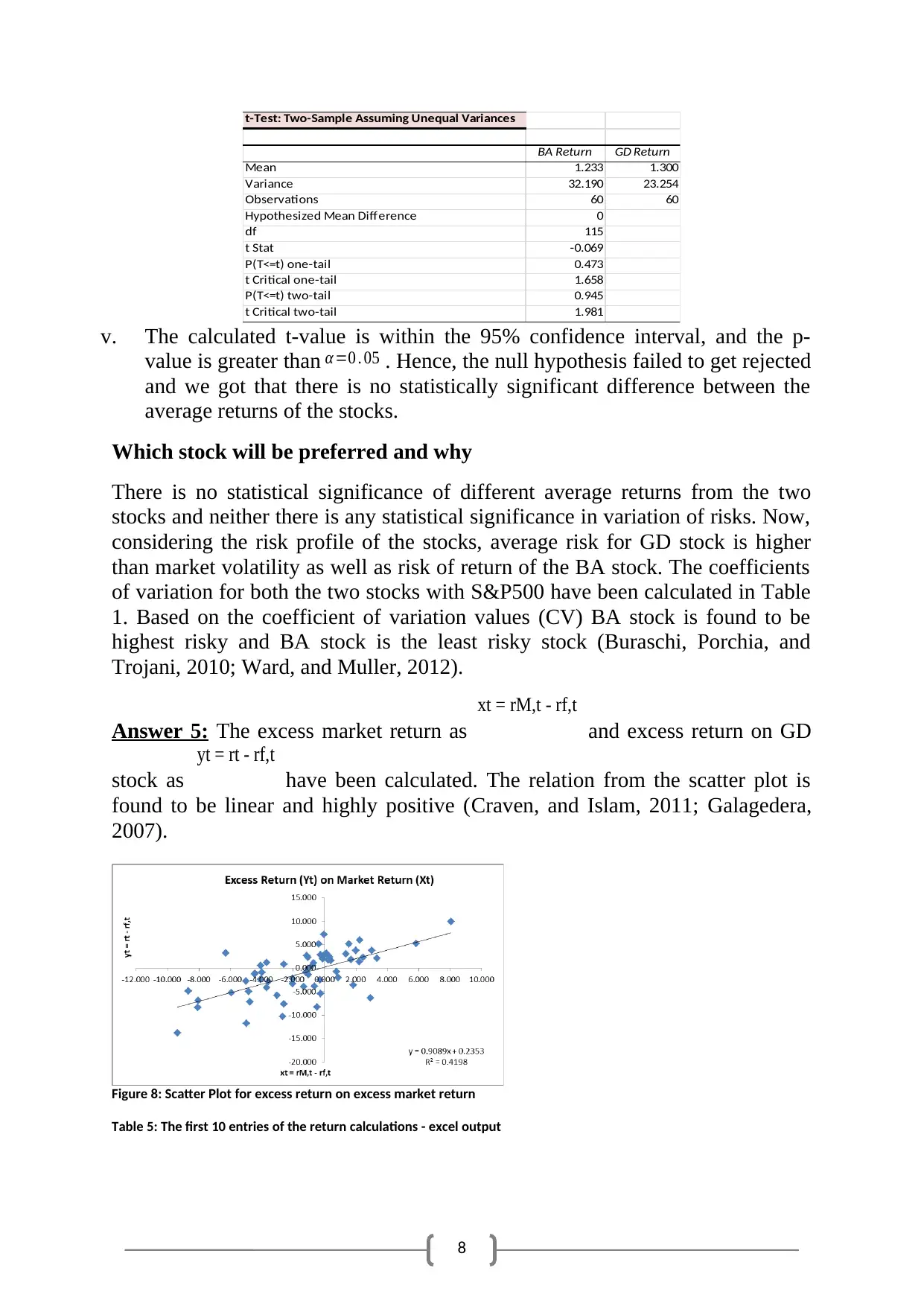
t-Test: Two-Sample Assuming Unequal Variances
BA Return GD Return
Mean 1.233 1.300
Variance 32.190 23.254
Observations 60 60
Hypothesized Mean Difference 0
df 115
t Stat -0.069
P(T<=t) one-tail 0.473
t Critical one-tail 1.658
P(T<=t) two-tail 0.945
t Critical two-tail 1.981
v. The calculated t-value is within the 95% confidence interval, and the p-
value is greater than α =0 . 05 . Hence, the null hypothesis failed to get rejected
and we got that there is no statistically significant difference between the
average returns of the stocks.
Which stock will be preferred and why
There is no statistical significance of different average returns from the two
stocks and neither there is any statistical significance in variation of risks. Now,
considering the risk profile of the stocks, average risk for GD stock is higher
than market volatility as well as risk of return of the BA stock. The coefficients
of variation for both the two stocks with S&P500 have been calculated in Table
1. Based on the coefficient of variation values (CV) BA stock is found to be
highest risky and BA stock is the least risky stock (Buraschi, Porchia, and
Trojani, 2010; Ward, and Muller, 2012).
Answer 5: The excess market return as
xt = rM,t - rf,t
and excess return on GD
stock as
yt = rt - rf,t
have been calculated. The relation from the scatter plot is
found to be linear and highly positive (Craven, and Islam, 2011; Galagedera,
2007).
Figure 8: Scatter Plot for excess return on excess market return
Table 5: The first 10 entries of the return calculations - excel output

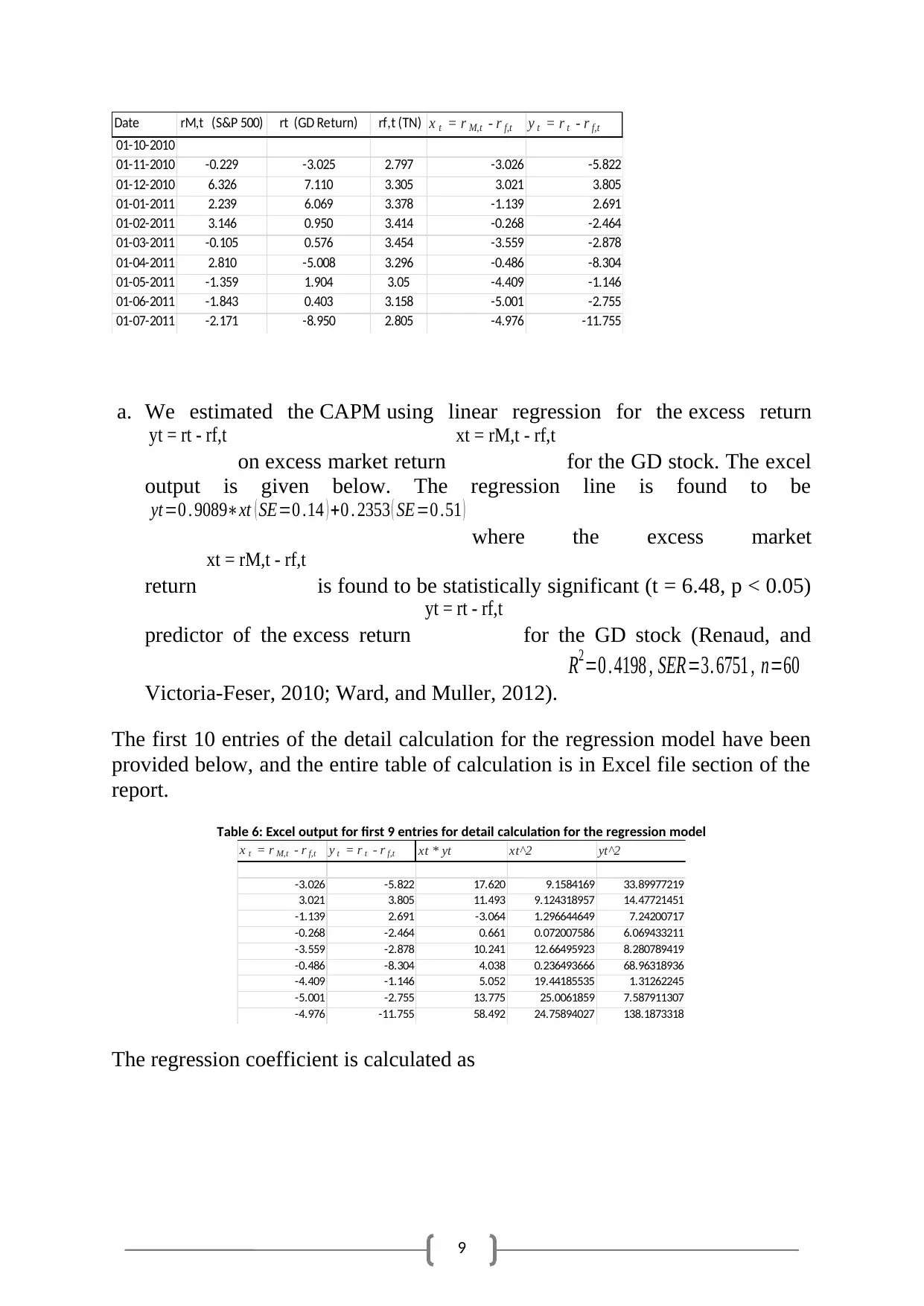
9
Date rM,t (S&P 500) rt (GD Return) rf,t (TN) x t = r M,t - r f,t y t = r t - r f,t
01-10-2010
01-11-2010 -0.229 -3.025 2.797 -3.026 -5.822
01-12-2010 6.326 7.110 3.305 3.021 3.805
01-01-2011 2.239 6.069 3.378 -1.139 2.691
01-02-2011 3.146 0.950 3.414 -0.268 -2.464
01-03-2011 -0.105 0.576 3.454 -3.559 -2.878
01-04-2011 2.810 -5.008 3.296 -0.486 -8.304
01-05-2011 -1.359 1.904 3.05 -4.409 -1.146
01-06-2011 -1.843 0.403 3.158 -5.001 -2.755
01-07-2011 -2.171 -8.950 2.805 -4.976 -11.755
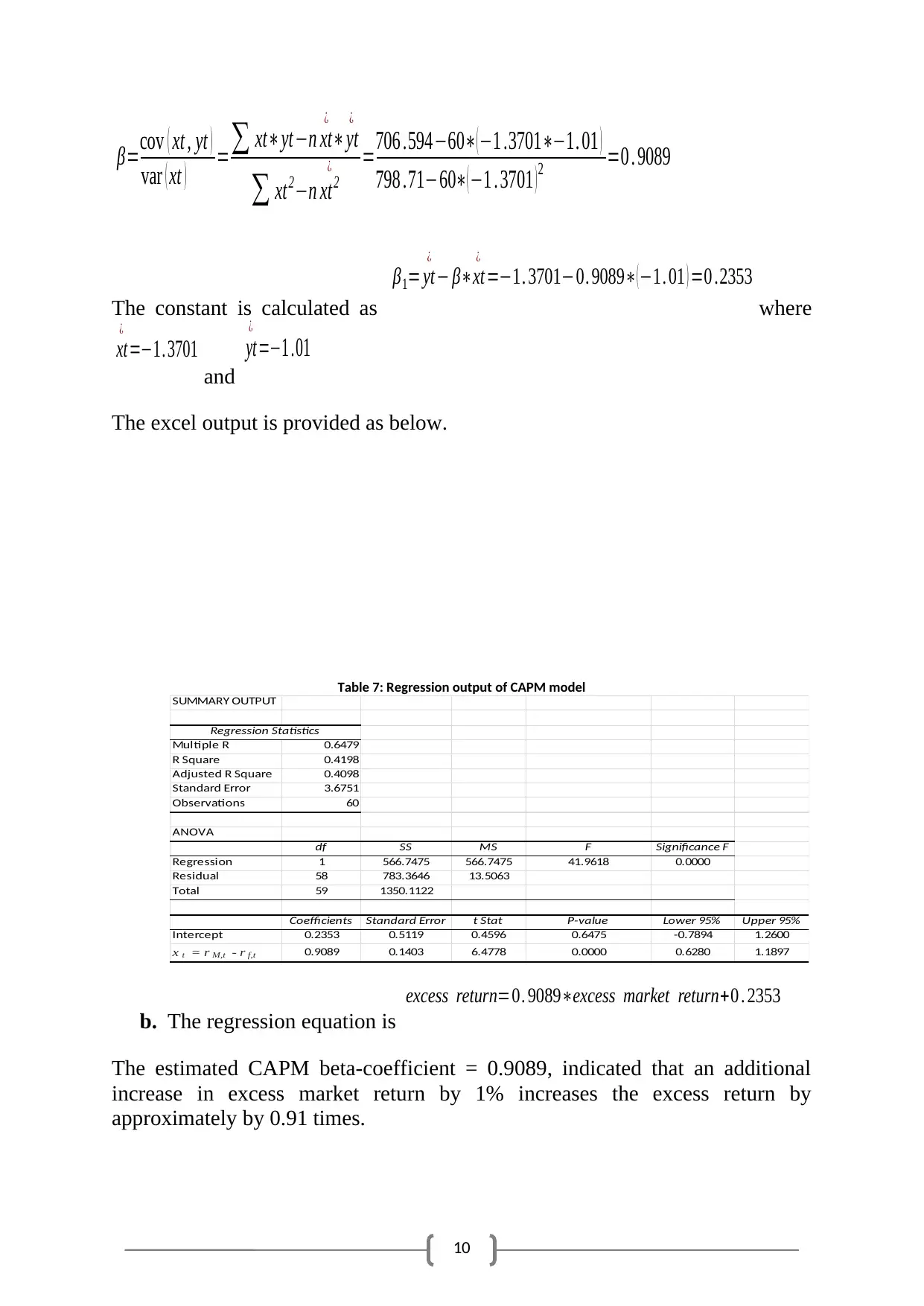
a. We estimated the CAPM using linear regression for the excess return
yt = rt - rf,t
on excess market return
xt = rM,t - rf,t
for the GD stock. The excel
output is given below. The regression line is found to be
yt=0 . 9089∗xt ( SE=0 .14 ) +0 . 2353 ( SE=0 .51 )
where the excess market
return
xt = rM,t - rf,t
is found to be statistically significant (t = 6.48, p < 0.05)
predictor of the excess return
yt = rt - rf,t
for the GD stock (Renaud, and
Victoria-Feser, 2010; Ward, and Muller, 2012).
R2=0 . 4198 , SER=3. 6751 , n=60
The first 10 entries of the detail calculation for the regression model have been
provided below, and the entire table of calculation is in Excel file section of the
report.
Table 6: Excel output for first 9 entries for detail calculation for the regression model
x t = r M,t - r f,t y t = r t - r f,t xt * yt xt^2 yt^2
-3.026 -5.822 17.620 9.1584169 33.89977219
3.021 3.805 11.493 9.124318957 14.47721451
-1.139 2.691 -3.064 1.296644649 7.24200717
-0.268 -2.464 0.661 0.072007586 6.069433211
-3.559 -2.878 10.241 12.66495923 8.280789419
-0.486 -8.304 4.038 0.236493666 68.96318936
-4.409 -1.146 5.052 19.44185535 1.31262245
-5.001 -2.755 13.775 25.0061859 7.587911307
-4.976 -11.755 58.492 24.75894027 138.1873318
The regression coefficient is calculated as

10
β=cov ( xt , yt )
var ( xt ) =∑ xt∗yt−n xt
¿
∗yt
¿
∑ xt2−n xt2
¿ =706 .594−60∗( −1 .3701∗−1. 01 )
798 .71−60∗( −1 . 3701 ) 2 =0 . 9089
The constant is calculated as
β1= yt
¿
− β∗xt
¿
=−1. 3701−0. 9089∗( −1. 01 ) =0 .2353
where
xt
¿
=−1. 3701
and
yt
¿
=−1 .01
The excel output is provided as below.
Table 7: Regression output of CAPM model
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.6479
R Square 0.4198
Adjusted R Square 0.4098
Standard Error 3.6751
Observations 60
ANOVA
df SS MS F Significance F
Regression 1 566.7475 566.7475 41.9618 0.0000
Residual 58 783.3646 13.5063
Total 59 1350.1122
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 0.2353 0.5119 0.4596 0.6475 -0.7894 1.2600
x t = r M,t - r f,t 0.9089 0.1403 6.4778 0.0000 0.6280 1.1897
b. The regression equation is
excess return=0. 9089∗excess market return+0 . 2353
The estimated CAPM beta-coefficient = 0.9089, indicated that an additional
increase in excess market return by 1% increases the excess return by
approximately by 0.91 times.

11
Compared to the risk of the GD portfolio, the CAPM beta is an indicator and a
benchmark for measuring instability or systemic risks across the market. The
beta dividend will be used by the asset pricing model (CAPM), which calculates
the expected return on expected market return. The beta in the regression model
reflects the GD stock’s tendency to fluctuate in the market. The beta is
calculated as:
β=cov ( asset and market )
var ( market )
The beta value of 0.9089 indicates that the GD stock moves in same direction as
the rest of the market (S&P500). Also the beta value of less than 1 indicated that
the GD stock is less volatile compared to the market (S&P500 profile).
c.
R2=0 . 4198
Indicates that there 41.98% variation in excess return is
explained by the excess market returns for GD stock, where the rest of the
58.02% variation remains unexplained (Miles, 2014).
d. The 95% confidence interval (CI) is noted to be [0.628, 1.1897] for the
slope coefficient. This is illustrated as the relation and estimation of excess
return for increase in excess market return. With 95% confidence, it is possible
to state that accurate impact of increase in excess market return by 1% would
be approximately somewhere between 0.63% and 1.19%.
Answer 6: A stock with volatility exactly the same as varied as the market is
known to be neutral stock. This means that the stock's riskiness is quantified at
the exact same rate as the wider market. This is expressed by stating that the
stock as a beta of exactly 1 (Frazzini, and Pedersen, 2014; Fernandez, 2015).
i. Null hypothesis: H0:
( β=1 )
and tested against the two tailed alternate
hypotheses HA:
( β≠1 )
ii. Level of significance
α=0 . 05
iii. We assume that the errors of the regression model are normally distributed,
and take the test statistic as
t= β
^¿− β0
se ¿ ¿ ¿ ¿ ¿
that approximately follows
N ( 0,1 )
due to
the fact that
n=60>30
. Hence, calculated
t= 0. 9089−1
0 . 1403 =−0 .6493

12
iv. The critical t-value at 5% level and 59 degrees of freedom is = 2.001.
The95% confidence interval is calculated as
−2. 001<t= 0 . 9089−β
0. 1403 < 2. 001
or
0 .628< β<1 . 1897
.
v. CI approach to test a hypothesis:
With 95% it is possible to infer that the estimated value of beta coefficient
will be somewhere between 0.628 and 1.1897. The population beta for
neutral stock is 1.0 that lies between the limits of the confidence interval.
Hence, at
α =0 . 05
the population beta of 1.0 is found to be well within the
95% confidence interval which indicates that the null hypothesis assuming
that the GD stock is neutral cannot be rejected. Therefore, we conclude that
the GD stock is indeed neutral (Pollet, and Wilson, 2010).
Answer 7: To check the assumption of ordinary least squares (OLS) method
that is normally distributed error term in the model, we perform a hypothesis
test (Park, 2015).
Figure 9: Histogram of residuals of the CAPM regression model
i. Null hypothesis: H0: “random errors are normally distributed” and is
tested against the two tailed Alternate hypothesis: HA: “random errors are
not normally distributed”.
ii. Level of significance is taken as 5%
( α=0 . 05 )
iii. The test statistic is considered as Jarque-Berra test of normality on the
residuals of the present linear regression model (Mantalos, 2011).
iv. The test statistic is calculated from the skewness and excess kurtosis of
the residuals. The skewness = -0.5317 and excess kurtosis = 0.4335 are

13
taken to calculate the test statistic as
JB= n
6 ( skewness2+ ( excess kurtosis2 ) / 4 )=3 . 297
. The p-value is calculated using
excel using chi-square distribution at 2 degrees of freedom as
p=chidist( 3 . 297 ,2 )=0 . 192> 0 .05
v. As the p-value greater than 0.05, the null hypothesis failed to get rejected
at
α =0 . 05
, concluding that it is plausible to assume that the errors are
normally distributed that satisfies the assumption of ordinary least
squares (OLS) method.
Table 8: Excel output of JB test of residuals
Descriptive Statistics Residuals
Mean 0.0000
SD 3.6438
Skewness -0.5317
Excess Kurtosis 0.4335
N 60
JB-Value p-value
Jarque-Berra_Residual E6/6 (E4^2)+(E5^2)/4 E9*F9 CHIDIST(G9,2)
Jarque-Berra_Residual 10.000 0.330 3.297 0.192
References
Abdymomunov, A., & Morley, J. (2011). Time variation of CAPM betas across
market volatility regimes. Applied Financial Economics, 21(19), 1463–
1478.

14
Bratton, W. W., & Wachter, M. L. (2012). A Theory of Preferred Stock. U. Pa.
L. Rev., 161, 1815.
Buraschi, A., Porchia, P., & Trojani, F. (2010). Correlation risk and optimal
portfolio choice. The Journal of Finance, 65(1), 393–420.
Craven, B. D., & Islam, S. M. (2011). Ordinary least-squares regression (pp.
224-228). Sage Publications.
Dempsey, M. (2013). The capital asset pricing model (CAPM): the history of a
failed revolutionary idea in finance? Abacus, 49, 7–23.
Fernandez, P. (2015). CAPM: an absurd model. Business Valuation Review,
34(1), 4–23.
Frazzini, A., & Pedersen, L. H. (2014). Betting against beta. Journal of
Financial Economics, 111(1), 1–25.
Galagedera, D. U. (2007). An alternative perspective on the relationship
between downside beta and CAPM beta. Emerging Markets Review, 8(1),
4–19.
Mantalos, P. (2011). Three different measures of sample skewness and kurtosis
and their effects on the Jarque? Bera test for normality. International
Journal of Computational Economics and Econometrics, 2(1), 47–62.
Miles, J. (2014). R squared, adjusted R squared. Wiley StatsRef: Statistics
Reference Online.
Moder, K. (2010). Alternatives to F-test in one way ANOVA in case of
heterogeneity of variances (a simulation study). Psychological Test and
Assessment Modeling, 52(4), 343-353.
Park, H. M. (2015). Univariate analysis and normality test using SAS, Stata,
and SPSS.
Pollet, J. M., & Wilson, M. (2010). Average correlation and stock market
returns. Journal of Financial Economics, 96(3), 364–380.

15
Renaud, O., & Victoria-Feser, M.-P. (2010). A robust coefficient of
determination for regression. Journal of Statistical Planning and Inference,
140(7), 1852–1862.
Ward, M., & Muller, C. (2012). Empirical testing of the CAPM on the JSE.
Investment Analysts Journal, 41(76), 1–12.