Economics and Quantitative Analysis: Linear Regression Report 2019
VerifiedAdded on 2023/04/20
|7
|1961
|158
Report
AI Summary
This report conducts a linear regression analysis to examine the relationship between college retention rates (RR) and graduation rates (GR) using data from 29 online colleges. The analysis includes descriptive statistics, scatter plots, and the estimation of a regression equation (y=0.2845x + 25.423). The report interprets the slope of the equation, tests the statistical significance of the relationship, and assesses the fitness of the regression equation for predicting GR values. It also discusses specific cases, such as South University and University of Phoenix, based on their RR and GR values. The findings indicate a strong positive correlation between RR and GR, with policy implications for university administrations to improve student retention and graduation rates. The report concludes with recommendations for improving retention and graduation rates, including monitoring student progress and curriculum review.

Economics and Quantitative Analysis
Economics and Quantitative Analysis
Institution Name
Student Name
1
Economics and Quantitative Analysis
Institution Name
Student Name
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Economics and Quantitative Analysis
Linear Regression Report
Purpose
The retention and graduation rates can both be applied as scales for evaluating the
quality of education offered by an institution. The major objective of this report will be to
conduct a linear regression analysis. Moreover, will estimate the regression equation that can
be used to predict the GR values in situations where the RR values are present.
Background
The change in the higher education has been propelled by a number of drivers in
recent times; technology, economy, globalization and changing demographics being just a
few. Even though each of these drivers have a significant impact, most researchers are in
agreement that online learning has disrupted the normal system of education (University of
Arkansas 2014). This technology has led to emergence of simple, accessible and affordable
education patterns. From 1970s to date the technology have tremendously developed with
several institutions joining in to offer online programmes (Rubin 2012). Despite the
improvement in education accessibility students and parents have been thrown into a
dilemma when it comes to selecting the right college to attend. To assist with this selection
problem two rates of interest have emerged, that is the retention rate (RR) and the graduation
rate (GR) (Dunlap & Lowenthal 2010).
The association between RR and GR do vary in a number of ways when dealing with
the online courses as compared to the traditional system. Graduation rate is the proportion of
students who join a college in first year and manages to graduate within 150% of the time
normally needed to complete a programme. (Callahan & Belcheir 2017). Meanwhile the RR
is the percentage of the first time first year students who enrol to continue with their second-
year studies in the same college.
Method
The RR and GR are important because they can be used to rank institutions based on
quality of education provided. In this study, a sample of 29 colleges from the online
educational database were selected at random and used to analyse the relationship between
the RR and GR (Berg, 2009). The Online Educational Database is an enterprise independently
tasked with generating a list of accredited institutions in Australia. Some of the approaches
that the analysis took is drawing a scatter plot, estimating regression line as well as modelling
2
Linear Regression Report
Purpose
The retention and graduation rates can both be applied as scales for evaluating the
quality of education offered by an institution. The major objective of this report will be to
conduct a linear regression analysis. Moreover, will estimate the regression equation that can
be used to predict the GR values in situations where the RR values are present.
Background
The change in the higher education has been propelled by a number of drivers in
recent times; technology, economy, globalization and changing demographics being just a
few. Even though each of these drivers have a significant impact, most researchers are in
agreement that online learning has disrupted the normal system of education (University of
Arkansas 2014). This technology has led to emergence of simple, accessible and affordable
education patterns. From 1970s to date the technology have tremendously developed with
several institutions joining in to offer online programmes (Rubin 2012). Despite the
improvement in education accessibility students and parents have been thrown into a
dilemma when it comes to selecting the right college to attend. To assist with this selection
problem two rates of interest have emerged, that is the retention rate (RR) and the graduation
rate (GR) (Dunlap & Lowenthal 2010).
The association between RR and GR do vary in a number of ways when dealing with
the online courses as compared to the traditional system. Graduation rate is the proportion of
students who join a college in first year and manages to graduate within 150% of the time
normally needed to complete a programme. (Callahan & Belcheir 2017). Meanwhile the RR
is the percentage of the first time first year students who enrol to continue with their second-
year studies in the same college.
Method
The RR and GR are important because they can be used to rank institutions based on
quality of education provided. In this study, a sample of 29 colleges from the online
educational database were selected at random and used to analyse the relationship between
the RR and GR (Berg, 2009). The Online Educational Database is an enterprise independently
tasked with generating a list of accredited institutions in Australia. Some of the approaches
that the analysis took is drawing a scatter plot, estimating regression line as well as modelling
2
Economics and Quantitative Analysis
a simple linear regression. The Microsoft excel was applied as a tool to help with the
analysis.
Results
a) The table gives a summary of the descriptive statistics. This involves measures of
central tendency as well as the measures of dispersion.
Descriptive Statistics
RR(%) GR(%)
Mean 57.4138 Mean 41.7586
Standard Error 4.3156 Standard Error 1.8320
Median 60 Median 39
Mode 51 Mode 36
Standard Deviation 23.2402 Standard Deviation 9.8657
Sample Variance 540.1084 Sample Variance 97.3325
Kurtosis 0.4618 Kurtosis -0.8824
Skewness -0.3099 Skewness 0.1764
Range 96 Range 36
Minimum 4 Minimum 25
Maximum 100 Maximum 61
Sum 1665 Sum 1211
Count 29 Count 29
Largest(1) 100 Largest(1) 61
Smallest(1) 4 Smallest(1) 25
Confidence Level(95.0%) 8.8401 Confidence Level(95.0%) 3.7527
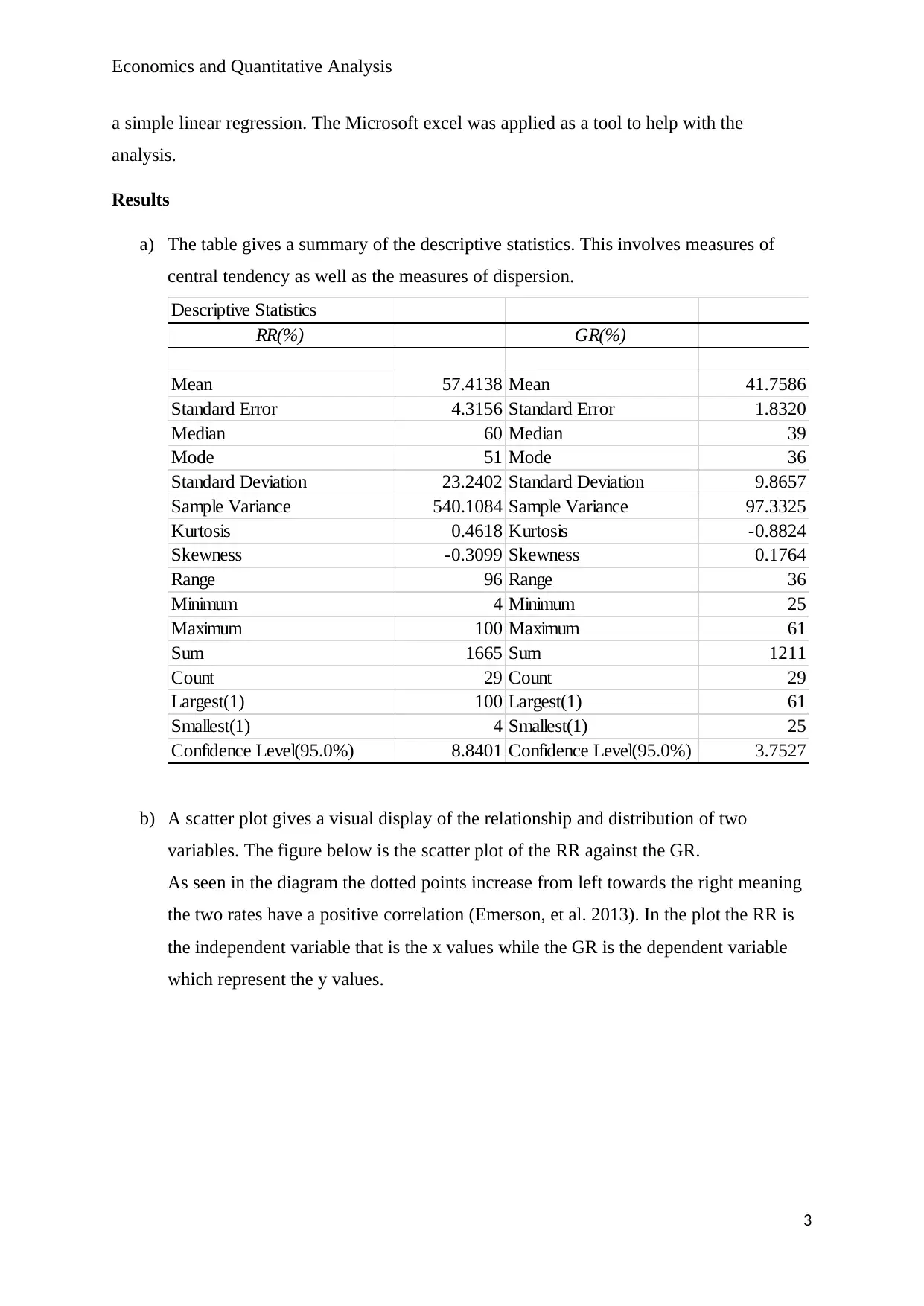
b) A scatter plot gives a visual display of the relationship and distribution of two
variables. The figure below is the scatter plot of the RR against the GR.
As seen in the diagram the dotted points increase from left towards the right meaning
the two rates have a positive correlation (Emerson, et al. 2013). In the plot the RR is
the independent variable that is the x values while the GR is the dependent variable
which represent the y values.
3
a simple linear regression. The Microsoft excel was applied as a tool to help with the
analysis.
Results
a) The table gives a summary of the descriptive statistics. This involves measures of
central tendency as well as the measures of dispersion.
Descriptive Statistics
RR(%) GR(%)
Mean 57.4138 Mean 41.7586
Standard Error 4.3156 Standard Error 1.8320
Median 60 Median 39
Mode 51 Mode 36
Standard Deviation 23.2402 Standard Deviation 9.8657
Sample Variance 540.1084 Sample Variance 97.3325
Kurtosis 0.4618 Kurtosis -0.8824
Skewness -0.3099 Skewness 0.1764
Range 96 Range 36
Minimum 4 Minimum 25
Maximum 100 Maximum 61
Sum 1665 Sum 1211
Count 29 Count 29
Largest(1) 100 Largest(1) 61
Smallest(1) 4 Smallest(1) 25
Confidence Level(95.0%) 8.8401 Confidence Level(95.0%) 3.7527
b) A scatter plot gives a visual display of the relationship and distribution of two
variables. The figure below is the scatter plot of the RR against the GR.
As seen in the diagram the dotted points increase from left towards the right meaning
the two rates have a positive correlation (Emerson, et al. 2013). In the plot the RR is
the independent variable that is the x values while the GR is the dependent variable
which represent the y values.
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Economics and Quantitative Analysis
c) From the scatter plot drawn above it’s possible to estimate the line of best fit. When
this is done using excel, we have the regression equation derived to be
y=0.2845 x +25.423 . The equation can be applied to estimate the values of GR (y)
when given the values of the RR (x).
d) The estimated regression equation is y=0.2845 x +25.423 . The equation ‘slope is
0.2845. This is the value that explains how the two rates relate (Tofallis 2009). For
example, from the gradient of 0.2845, it can be interpreted that for a 1% increase
(decrease) in the RR the GR will increase (decrease) by 0.2845% which is a sign of
positive correlation.
e) To test for a statistically significance relationship between the two rates, will develop
a linear regression model. This is presented in the table below.
Regression Statistics
Multiple R 0.6702
R Square 0.4492
Adjusted R Square 0.4288
Standard Error 7.4561
Observations 29
ANOVA
df SS MS F Significance F
Regression 1 1224.2860 1224.2860 22.0221 0.0001
Residual 27 1501.0244 55.5935
Total 28 2725.3103
Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0%
Intercept 25.42290363 3.7463 6.7862 0.0000 17.7362 33.1096 17.7362 33.1096
RR(%) 0.284526003 0.0606 4.6928 0.0001 0.1601 0.4089 0.1601 0.4089
From the table the value of the coefficient correlation is 0.6702 which indicates a
strong positive correlation between RR and GR. The p-value of RR is 0.0001 which is
lower than 0.05. From this, we can deduce that at a 95% confidence interval the
4
c) From the scatter plot drawn above it’s possible to estimate the line of best fit. When
this is done using excel, we have the regression equation derived to be
y=0.2845 x +25.423 . The equation can be applied to estimate the values of GR (y)
when given the values of the RR (x).
d) The estimated regression equation is y=0.2845 x +25.423 . The equation ‘slope is
0.2845. This is the value that explains how the two rates relate (Tofallis 2009). For
example, from the gradient of 0.2845, it can be interpreted that for a 1% increase
(decrease) in the RR the GR will increase (decrease) by 0.2845% which is a sign of
positive correlation.
e) To test for a statistically significance relationship between the two rates, will develop
a linear regression model. This is presented in the table below.
Regression Statistics
Multiple R 0.6702
R Square 0.4492
Adjusted R Square 0.4288
Standard Error 7.4561
Observations 29
ANOVA
df SS MS F Significance F
Regression 1 1224.2860 1224.2860 22.0221 0.0001
Residual 27 1501.0244 55.5935
Total 28 2725.3103
Coefficients Standard Error t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0%
Intercept 25.42290363 3.7463 6.7862 0.0000 17.7362 33.1096 17.7362 33.1096
RR(%) 0.284526003 0.0606 4.6928 0.0001 0.1601 0.4089 0.1601 0.4089
From the table the value of the coefficient correlation is 0.6702 which indicates a
strong positive correlation between RR and GR. The p-value of RR is 0.0001 which is
lower than 0.05. From this, we can deduce that at a 95% confidence interval the
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Economics and Quantitative Analysis
association between the RR and the GR is statistically significant. What the p-value
proves is the hypothesis that the coefficient of x in the equation y=0.2845 x +25.423
is not 0.
f) The regression equation provides a good fit for predicting the values of GR when
given RR. The fitness of the regression equation is tested using the F statistics. From
the table the value of Significant F is 0.0001 which is lower than 0.05 (Malakooti
2013). Hence at 95% confidence interval there is sufficient evidence to indicate that
the equation is a good fit for modelling the graduation rates.
g) The RR for South University is 51% while the GR is 25%. Looking at the GR, the
25% means the university has the poorest graduation rate out of all the sampled 29
colleges. Being that the mean of the GR stands at 41.76, it can be implied that the
college is performing poorly in assisting its students complete their programmes in
time. This is an issue that I need to be worried of being the University President.
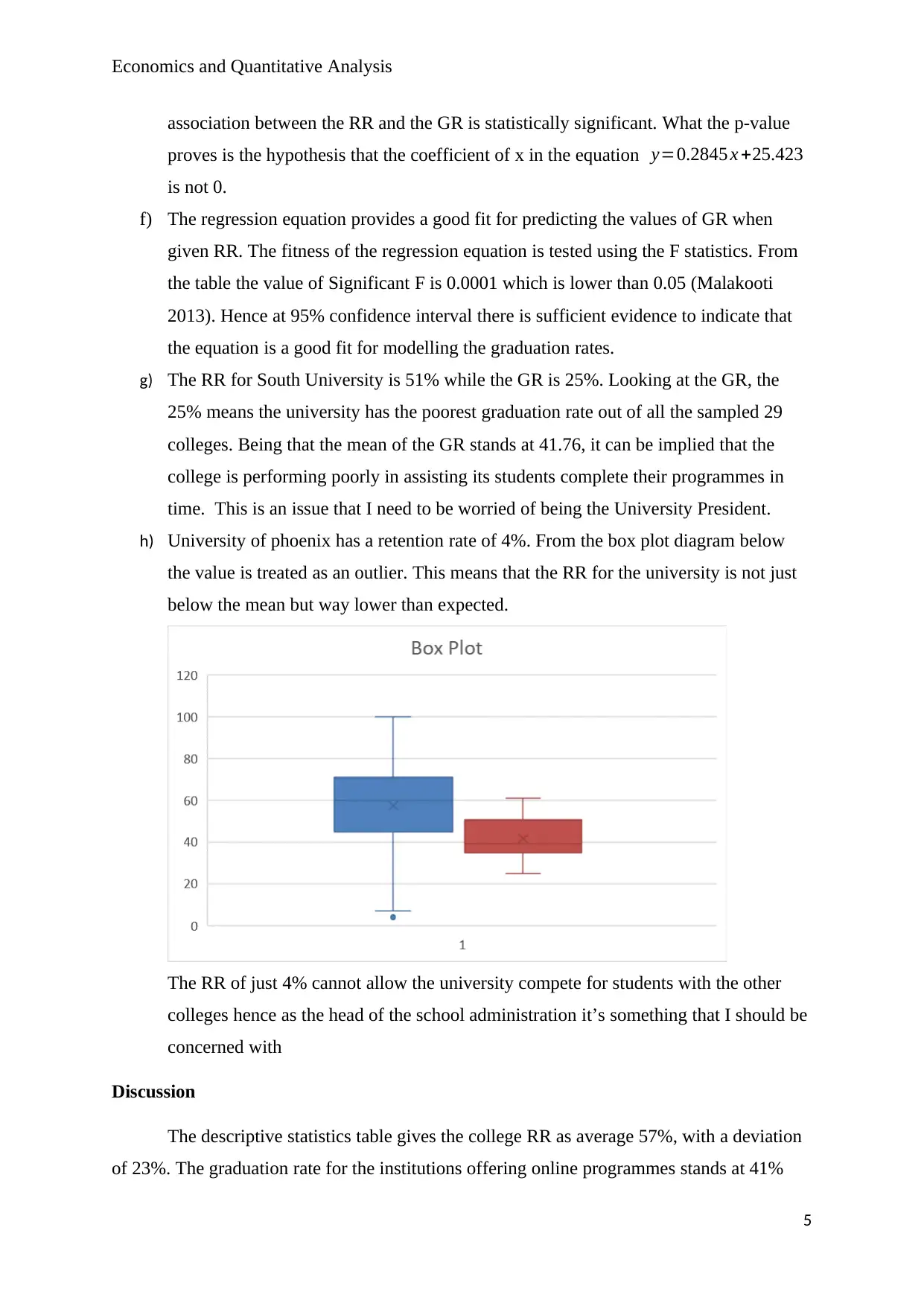
h) University of phoenix has a retention rate of 4%. From the box plot diagram below
the value is treated as an outlier. This means that the RR for the university is not just
below the mean but way lower than expected.
The RR of just 4% cannot allow the university compete for students with the other
colleges hence as the head of the school administration it’s something that I should be
concerned with
Discussion
The descriptive statistics table gives the college RR as average 57%, with a deviation
of 23%. The graduation rate for the institutions offering online programmes stands at 41%
5
association between the RR and the GR is statistically significant. What the p-value
proves is the hypothesis that the coefficient of x in the equation y=0.2845 x +25.423
is not 0.
f) The regression equation provides a good fit for predicting the values of GR when
given RR. The fitness of the regression equation is tested using the F statistics. From
the table the value of Significant F is 0.0001 which is lower than 0.05 (Malakooti
2013). Hence at 95% confidence interval there is sufficient evidence to indicate that
the equation is a good fit for modelling the graduation rates.
g) The RR for South University is 51% while the GR is 25%. Looking at the GR, the
25% means the university has the poorest graduation rate out of all the sampled 29
colleges. Being that the mean of the GR stands at 41.76, it can be implied that the
college is performing poorly in assisting its students complete their programmes in
time. This is an issue that I need to be worried of being the University President.
h) University of phoenix has a retention rate of 4%. From the box plot diagram below
the value is treated as an outlier. This means that the RR for the university is not just
below the mean but way lower than expected.
The RR of just 4% cannot allow the university compete for students with the other
colleges hence as the head of the school administration it’s something that I should be
concerned with
Discussion
The descriptive statistics table gives the college RR as average 57%, with a deviation
of 23%. The graduation rate for the institutions offering online programmes stands at 41%
5

Economics and Quantitative Analysis
with a standard deviation of 9% meaning the RR has a wider spread compared to the GR.
Modelling a simple linear regression gives the correlation coefficient to be 0.6702 which is
interpreted as a strong positive correlation. The findings of this study is consistent with
studies done by other scholars. For instance the study by Jewell (2015) supports the
conclusion that has been derived in our case.
The analysis made use of secondary data which is more reliable as it has been verified
and published. This is one of the key strengths of the study. One area that may limit the
authenticity of the study is the small sample size that may lead to misleading generalisations.
The findings in this report are consistent with the previous findings. One of the generalisation
that previous researchers have arrived at is the fact that retention rate and the graduation rates
are influenced by similar factors (Sidle & McReynolds 2009) This has been confirmed by our
findings which concluded that the two rates are strongly positively correlated. The policy
implications of these findings can be narrowed down to the influence of the rates when it
comes to assisting the university administrations come up with clear policies that can assist
improve the students retention rates as a way of increasing the number of students graduating
from the a college.
Recommendations
To rectify the issues that have been identified by the data analysis, the following
recommendations need to be looked at;
The president of Phoenix University should develop a department to monitor
students’ progress and hence assist improve the institution’s retention rate.
The president of South University should initiate a curriculum review to ensure the
students are receiving quality education.
The ministry of education should conduct farther research in to the quality provision
by the universities offering online programmes.
6
with a standard deviation of 9% meaning the RR has a wider spread compared to the GR.
Modelling a simple linear regression gives the correlation coefficient to be 0.6702 which is
interpreted as a strong positive correlation. The findings of this study is consistent with
studies done by other scholars. For instance the study by Jewell (2015) supports the
conclusion that has been derived in our case.
The analysis made use of secondary data which is more reliable as it has been verified
and published. This is one of the key strengths of the study. One area that may limit the
authenticity of the study is the small sample size that may lead to misleading generalisations.
The findings in this report are consistent with the previous findings. One of the generalisation
that previous researchers have arrived at is the fact that retention rate and the graduation rates
are influenced by similar factors (Sidle & McReynolds 2009) This has been confirmed by our
findings which concluded that the two rates are strongly positively correlated. The policy
implications of these findings can be narrowed down to the influence of the rates when it
comes to assisting the university administrations come up with clear policies that can assist
improve the students retention rates as a way of increasing the number of students graduating
from the a college.
Recommendations
To rectify the issues that have been identified by the data analysis, the following
recommendations need to be looked at;
The president of Phoenix University should develop a department to monitor
students’ progress and hence assist improve the institution’s retention rate.
The president of South University should initiate a curriculum review to ensure the
students are receiving quality education.
The ministry of education should conduct farther research in to the quality provision
by the universities offering online programmes.
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Economics and Quantitative Analysis
References
Berg, B 2009, Qualitative Research Methods for the Social Sciences. Seventh ed. Boston: Pearson
Education Inc.
Callahan, J & Belcheir, M 2017, Testing Our Assumptions. Journal of College Student Retention:
Research, Theory & Practice, Vol. 19, pp. 161–175.
Dunlap, J & Lowenthal, P 2010, Defeating the Kobayashi Maru: Supporting Student Retention by
Balancing the Needs of the Many and the One. Educause Quarterly, vol. 33, no. 4, pp. 33.
Emerson, J, Green, W, Schoerke, B & Crowley, J 2013, The Generalized Pairs Plot. Journal of
Computational and Graphical Statistics, vol. 22, no. 1, pp. 79–91.
Jewell, S 2015, Retention and Graduation Rates at Public Research Universities: Do Medical Centers
Affect Rates?. [Online]
Available at: http://martin.uky.edu/sites/martin.uky.edu/files/Capstone_Projects/Capstones_2015/
Jewell.pdf
[Accessed 29 January 2018].
Malakooti, B 2013, Operations and Production Systems with Multiple Objectives, John Wiley & Sons.
Rubin, M 2012, Social class differences in social integration among students in higher education: A
meta-analysis and recommendations for future research. Journal of Diversity in Higher Education,
Vol. 5, pp. 22–38.
Sidle, M. & McReynolds, J 2009, The freshman year experience: Student retention andstudent
success. NASPA Journal, vol. 46, no. 3, pp. 434-446.
Tofallis, C 2009, Least Squares Percentage Regression. Journal of Modern Applied Statistical
Methods, Vol. 7 , pp. 526–534.
University of Arkansas 2014, Increasing Graduation Rates, University of Arkansas Quality Initiative
Proposal. [Online]
Available at: https://provost.uark.edu/accreditation.php
[Accessed 30 January 2018].
7
References
Berg, B 2009, Qualitative Research Methods for the Social Sciences. Seventh ed. Boston: Pearson
Education Inc.
Callahan, J & Belcheir, M 2017, Testing Our Assumptions. Journal of College Student Retention:
Research, Theory & Practice, Vol. 19, pp. 161–175.
Dunlap, J & Lowenthal, P 2010, Defeating the Kobayashi Maru: Supporting Student Retention by
Balancing the Needs of the Many and the One. Educause Quarterly, vol. 33, no. 4, pp. 33.
Emerson, J, Green, W, Schoerke, B & Crowley, J 2013, The Generalized Pairs Plot. Journal of
Computational and Graphical Statistics, vol. 22, no. 1, pp. 79–91.
Jewell, S 2015, Retention and Graduation Rates at Public Research Universities: Do Medical Centers
Affect Rates?. [Online]
Available at: http://martin.uky.edu/sites/martin.uky.edu/files/Capstone_Projects/Capstones_2015/
Jewell.pdf
[Accessed 29 January 2018].
Malakooti, B 2013, Operations and Production Systems with Multiple Objectives, John Wiley & Sons.
Rubin, M 2012, Social class differences in social integration among students in higher education: A
meta-analysis and recommendations for future research. Journal of Diversity in Higher Education,
Vol. 5, pp. 22–38.
Sidle, M. & McReynolds, J 2009, The freshman year experience: Student retention andstudent
success. NASPA Journal, vol. 46, no. 3, pp. 434-446.
Tofallis, C 2009, Least Squares Percentage Regression. Journal of Modern Applied Statistical
Methods, Vol. 7 , pp. 526–534.
University of Arkansas 2014, Increasing Graduation Rates, University of Arkansas Quality Initiative
Proposal. [Online]
Available at: https://provost.uark.edu/accreditation.php
[Accessed 30 January 2018].
7
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





