AT10251 Statistical Analysis Project Part C: Fuel Price Study
VerifiedAdded on 2023/04/25
|10
|1689
|107
Project
AI Summary
This statistical analysis project investigates fuel prices in Western Australia, comparing unleaded and diesel prices across capital cities and regional areas. The project employs z-tests to compare mean fuel prices between capital cities and regional areas, revealing whether prices differ significantly. Regression analysis and correlation are used to examine the relationship between unleaded and diesel fuel prices, determining the strength and nature of their correlation. Furthermore, a multiple linear regression model incorporates location as a variable to assess its impact on fuel prices. The analysis includes scatter plots, regression tables, and hypothesis testing to draw conclusions about fuel price variations and relationships. The project's findings indicate that the mean price of unleaded fuel in capital cities is not less than in regional areas, and it identifies a strong positive linear correlation between unleaded and diesel fuel prices. Location is found to have no significant influence on the model. The project utilizes data from PetrolSpy Australia, providing a comprehensive statistical evaluation of fuel price dynamics.

Running Head: Statistics
Statistical Analysis Project
Part C
Student’s Name
Institution Affiliation
Statistical Analysis Project
Part C
Student’s Name
Institution Affiliation
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Running Head: Statistics
Part C
This project responds to the questions about fuels prices in Western Australia. It compares
prices of unleaded fuel and diesel, within the capital towns and towns in other regionals. This has
been done by applying the knowledge of statistical inference, regression analysis and correlation.
The results are discussed below.
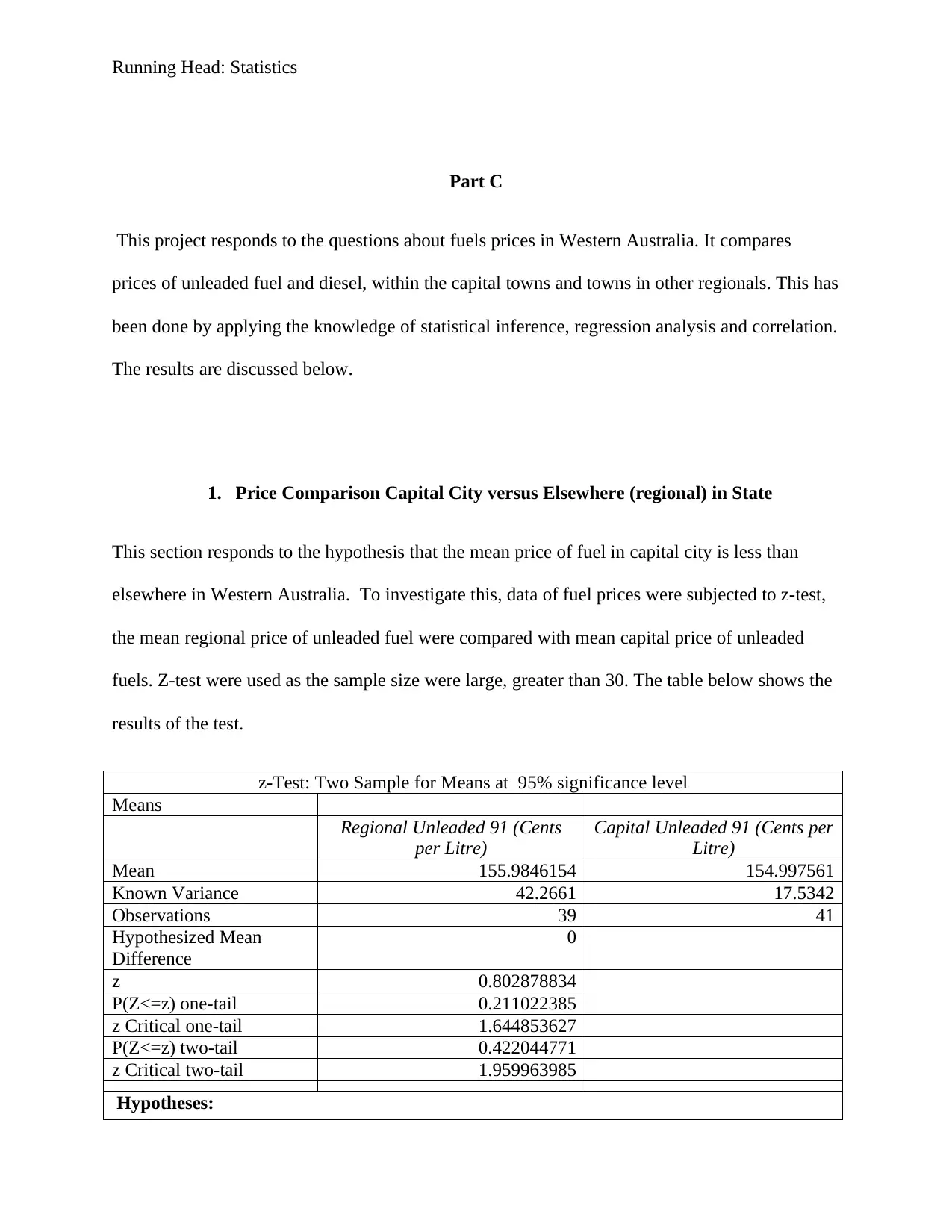
1. Price Comparison Capital City versus Elsewhere (regional) in State
This section responds to the hypothesis that the mean price of fuel in capital city is less than
elsewhere in Western Australia. To investigate this, data of fuel prices were subjected to z-test,
the mean regional price of unleaded fuel were compared with mean capital price of unleaded
fuels. Z-test were used as the sample size were large, greater than 30. The table below shows the
results of the test.
z-Test: Two Sample for Means at 95% significance level
Means
Regional Unleaded 91 (Cents
per Litre)
Capital Unleaded 91 (Cents per
Litre)
Mean 155.9846154 154.997561
Known Variance 42.2661 17.5342
Observations 39 41
Hypothesized Mean
Difference
0
z 0.802878834
P(Z<=z) one-tail 0.211022385
z Critical one-tail 1.644853627
P(Z<=z) two-tail 0.422044771
z Critical two-tail 1.959963985
Hypotheses:
Part C
This project responds to the questions about fuels prices in Western Australia. It compares
prices of unleaded fuel and diesel, within the capital towns and towns in other regionals. This has
been done by applying the knowledge of statistical inference, regression analysis and correlation.
The results are discussed below.
1. Price Comparison Capital City versus Elsewhere (regional) in State
This section responds to the hypothesis that the mean price of fuel in capital city is less than
elsewhere in Western Australia. To investigate this, data of fuel prices were subjected to z-test,
the mean regional price of unleaded fuel were compared with mean capital price of unleaded
fuels. Z-test were used as the sample size were large, greater than 30. The table below shows the
results of the test.
z-Test: Two Sample for Means at 95% significance level
Means
Regional Unleaded 91 (Cents
per Litre)
Capital Unleaded 91 (Cents per
Litre)
Mean 155.9846154 154.997561
Known Variance 42.2661 17.5342
Observations 39 41
Hypothesized Mean
Difference
0
z 0.802878834
P(Z<=z) one-tail 0.211022385
z Critical one-tail 1.644853627
P(Z<=z) two-tail 0.422044771
z Critical two-tail 1.959963985
Hypotheses:

Running Head: Statistics
Null hypothesis: Regional mean price-Capital mean price =0
Alternative hypothesis: Regional mean price-Capital mean price not equal to 0
Results Decision
Z-stat<Critical(two tail) Fail to reject null hypothesis
P-value(PZ<=z) two tail > 0.05 Fail to reject null hypothesis
From the result in the above table it’s clear that the mean price of unleaded fuel in capital city is
not less than the mean price in the regional level. The null hypothesis have been adopted as the
z-statistic (0.80) is less than the z- critical (1.96) and the p-value (0.42) is greater than 0.05.
2. Relationship between Unleaded 91 and Diesel
This section explores the relationship between the price of unleaded fuel and the price of diesel
in Western Australia. This is to investigate whether two variables have a linear or non-linear
correlation. To do this unleaded fuel prices were assumed independent variable ( x )while diesel
price were dependent variable ( y ). The investigation was done into stages. First is construction of
scatter plot to identify the relationship that exists between the variables from the pattern. Second
is doing the regression analysis of the data of prices to determine the correlation coefficient,
coefficient of determine, slope coefficient and intercept coefficient between the two variables.
2.1. Scatter plot
The following chart is a scatter plot of unleaded fuel prices against diesel prices.
Null hypothesis: Regional mean price-Capital mean price =0
Alternative hypothesis: Regional mean price-Capital mean price not equal to 0
Results Decision
Z-stat<Critical(two tail) Fail to reject null hypothesis
P-value(PZ<=z) two tail > 0.05 Fail to reject null hypothesis
From the result in the above table it’s clear that the mean price of unleaded fuel in capital city is
not less than the mean price in the regional level. The null hypothesis have been adopted as the
z-statistic (0.80) is less than the z- critical (1.96) and the p-value (0.42) is greater than 0.05.
2. Relationship between Unleaded 91 and Diesel
This section explores the relationship between the price of unleaded fuel and the price of diesel
in Western Australia. This is to investigate whether two variables have a linear or non-linear
correlation. To do this unleaded fuel prices were assumed independent variable ( x )while diesel
price were dependent variable ( y ). The investigation was done into stages. First is construction of
scatter plot to identify the relationship that exists between the variables from the pattern. Second
is doing the regression analysis of the data of prices to determine the correlation coefficient,
coefficient of determine, slope coefficient and intercept coefficient between the two variables.
2.1. Scatter plot
The following chart is a scatter plot of unleaded fuel prices against diesel prices.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Running Head: Statistics
140.0 145.0 150.0 155.0 160.0 165.0 170.0
130.0
140.0
150.0
160.0
170.0
180.0
DIESEL AGAINST UNLEADED FUEL IN WESTERN
AUSTRALIA
Unleaded Fuel(Cent Per Litre)
Diesel(Cents Per Litre)
From the scatter plot, the data points are forming close to linear pattern. This suggests a linear
correlation between diesel and unleaded fuel prices
2.2. Simple linear model
Below is a table to summarize the result of regression analysis of the data of prices between
diesel and unleaded fuel.
Regression Statistics
Multiple R 0.880972415
R Square 0.776112397
Adjusted R Square 0.773242043
Standard Error 2.364235799
Observations 80
Coefficients P-value
Intercept 31.42419388 9.3167E-05
Unleaded 91 (Cents per Litre) 0.805919176 4.562E-27
140.0 145.0 150.0 155.0 160.0 165.0 170.0
130.0
140.0
150.0
160.0
170.0
180.0
DIESEL AGAINST UNLEADED FUEL IN WESTERN
AUSTRALIA
Unleaded Fuel(Cent Per Litre)
Diesel(Cents Per Litre)
From the scatter plot, the data points are forming close to linear pattern. This suggests a linear
correlation between diesel and unleaded fuel prices
2.2. Simple linear model
Below is a table to summarize the result of regression analysis of the data of prices between
diesel and unleaded fuel.
Regression Statistics
Multiple R 0.880972415
R Square 0.776112397
Adjusted R Square 0.773242043
Standard Error 2.364235799
Observations 80
Coefficients P-value
Intercept 31.42419388 9.3167E-05
Unleaded 91 (Cents per Litre) 0.805919176 4.562E-27
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Running Head: Statistics
From the table, the intercept and slope intercept between the price of diesel and unleaded fuel
are 31.424 and 0.8059 respectively. Thus, the linear regression model between the two variables
will be written as;
y=0.8059 x +31.424 , where x=unlead fuel price∧ y=diesel price
The slope intercept of 0.8059 implies that when unleaded fuel price change by 1 cent per litre,
the price of diesel will change by 0.8059 cents per litre. On the other hand, the intercept
coefficient of 32.424 suggests that the price will be 32.424 cent per litre when the price of
unleaded fuel is 0 or when there’s no unleaded fuel in the market.
Moreover, from the table, the coefficient of correlation ( R ) is 0.881 and the coefficient of
determination is 0.7761. The correlation coefficient of + 0.881 is very close to +1, implying a
high positive linear relationship between price of diesel and that of unleaded fuel. At same
time, the coefficient of determination of 0.776 between the two variables indicates that diesel
price has 77.6% chance of variation in relation to unleaded fuel price.
Finally, the p-values of the intercept and slope coefficient are 9.3167E-05 and 4.562E-27
respectively, which are less than 0.05. This indicates that the price of unleaded fuel has a
significant contribution in the model and hence should be included.
3. Multiple Linear Regression Model
In this section Location is introduced as the second independent variable in the simple linear
regression model; y=0.8059 x +31.424 , where x=unlead fuel price∧ y=diesel price
From the table, the intercept and slope intercept between the price of diesel and unleaded fuel
are 31.424 and 0.8059 respectively. Thus, the linear regression model between the two variables
will be written as;
y=0.8059 x +31.424 , where x=unlead fuel price∧ y=diesel price
The slope intercept of 0.8059 implies that when unleaded fuel price change by 1 cent per litre,
the price of diesel will change by 0.8059 cents per litre. On the other hand, the intercept
coefficient of 32.424 suggests that the price will be 32.424 cent per litre when the price of
unleaded fuel is 0 or when there’s no unleaded fuel in the market.
Moreover, from the table, the coefficient of correlation ( R ) is 0.881 and the coefficient of
determination is 0.7761. The correlation coefficient of + 0.881 is very close to +1, implying a
high positive linear relationship between price of diesel and that of unleaded fuel. At same
time, the coefficient of determination of 0.776 between the two variables indicates that diesel
price has 77.6% chance of variation in relation to unleaded fuel price.
Finally, the p-values of the intercept and slope coefficient are 9.3167E-05 and 4.562E-27
respectively, which are less than 0.05. This indicates that the price of unleaded fuel has a
significant contribution in the model and hence should be included.
3. Multiple Linear Regression Model
In this section Location is introduced as the second independent variable in the simple linear
regression model; y=0.8059 x +31.424 , where x=unlead fuel price∧ y=diesel price

Running Head: Statistics
This is meant to determine whether location can influence the price of diesel and unleaded fuels.
Regression Statistics
Multiple R 0.88107394
R Square 0.77629129
Adjusted R Square 0.77048068
Standard Error 2.37858758
Observations 80
Coefficients P-value
Intercept 31.5343268 0.00010012
Location 0.13257776 0.80468263
Unleaded 91 (Cents per Litre) 0.80479513 1.3248E-26
From the table, the intercept and slope intercept between the price of diesel, location and
unleaded fuel are 31.534, 0.133, and 0.8048 respectively. Thus, the linear regression model
between the two variables will be written as;
y=0.8048 x1 +0.133 x2+31.534 , where x1=unlead fuel , x2=location∧ y =diesel
Also from the table, the coefficient of correlation ( R ) is 0.881 and the coefficient of
determination is 0.776. The correlation coefficient of + 0.881 is very close to +1, implying a
high positive linear relationship between price of diesel , location and that of unleaded fuel.
At same time, the coefficient of determination of 0.776 between the two variables indicates that
diesel price has 77.6% chance of variation in relation to unleaded fuel price. Comparing these
values with those of the simple linear model, they are approximately the same. This reveals that
location has no contribution in the model.
This is meant to determine whether location can influence the price of diesel and unleaded fuels.
Regression Statistics
Multiple R 0.88107394
R Square 0.77629129
Adjusted R Square 0.77048068
Standard Error 2.37858758
Observations 80
Coefficients P-value
Intercept 31.5343268 0.00010012
Location 0.13257776 0.80468263
Unleaded 91 (Cents per Litre) 0.80479513 1.3248E-26
From the table, the intercept and slope intercept between the price of diesel, location and
unleaded fuel are 31.534, 0.133, and 0.8048 respectively. Thus, the linear regression model
between the two variables will be written as;
y=0.8048 x1 +0.133 x2+31.534 , where x1=unlead fuel , x2=location∧ y =diesel
Also from the table, the coefficient of correlation ( R ) is 0.881 and the coefficient of
determination is 0.776. The correlation coefficient of + 0.881 is very close to +1, implying a
high positive linear relationship between price of diesel , location and that of unleaded fuel.
At same time, the coefficient of determination of 0.776 between the two variables indicates that
diesel price has 77.6% chance of variation in relation to unleaded fuel price. Comparing these
values with those of the simple linear model, they are approximately the same. This reveals that
location has no contribution in the model.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Running Head: Statistics
To determine the significance of the independent variables (Location and Unleaded fuel price,
their p-values compared at 5% significance level. The p-values of location and unleaded fuels
price are 0.8047 and 1.325E-26. The p-value of location is greater than 0.05 and that of unleaded
fuel is less than 0.05. This indicates that location has no significant contribution in the model but
price of unleaded does.
In conclusion, the test has clearly proven that the model that best fits the data is the simple linear
regression model.
APPENDIX C
Appendix C1: Question 1 Statistical Inference
Hypothesis 1: On the specified day was the mean price of your fuel less in the capital city than
elsewhere in the state specified by your sample.
H0 : μRegional −μCapital=0
H0 : μRegional −μCapital ≠ 0
Use 5% significance level
To determine the significance of the independent variables (Location and Unleaded fuel price,
their p-values compared at 5% significance level. The p-values of location and unleaded fuels
price are 0.8047 and 1.325E-26. The p-value of location is greater than 0.05 and that of unleaded
fuel is less than 0.05. This indicates that location has no significant contribution in the model but
price of unleaded does.
In conclusion, the test has clearly proven that the model that best fits the data is the simple linear
regression model.
APPENDIX C
Appendix C1: Question 1 Statistical Inference
Hypothesis 1: On the specified day was the mean price of your fuel less in the capital city than
elsewhere in the state specified by your sample.
H0 : μRegional −μCapital=0
H0 : μRegional −μCapital ≠ 0
Use 5% significance level
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Running Head: Statistics
Table 1: Excel Output
z-Test: Two Sample for Means: at 5% significance level
Regional Unleaded 91 (Cents per
Litre)
Capital Unleaded 91 (Cents per
Litre)
Mean 155.9846154 154.997561
Known Variance 42.2661 17.5342
Observations 39 41
Hypothesized Mean Difference 0
z 0.802878834
P(Z<=z) one-tail 0.211022385
z Critical one-tail 1.644853627
P(Z<=z) two-tail 0.422044771
z Critical two-tail 1.959963985
Null hypothesis Regional mean price-Capital mean price =0
Alternative hypothesis Regional mean price-Capital mean price not equal to 0
Observation Decision
Z-stat<Critical(two tail) Fail to reject null hypothesis
P-value(PZ<=z) two tail > 0.05
Appendix C2: Question 2 Simple Linear Regression Model
Hypothesis 2: Is the relationship between diesel and Unleaded fuel prices linear of non-linear?
Table 1: Excel Output
z-Test: Two Sample for Means: at 5% significance level
Regional Unleaded 91 (Cents per
Litre)
Capital Unleaded 91 (Cents per
Litre)
Mean 155.9846154 154.997561
Known Variance 42.2661 17.5342
Observations 39 41
Hypothesized Mean Difference 0
z 0.802878834
P(Z<=z) one-tail 0.211022385
z Critical one-tail 1.644853627
P(Z<=z) two-tail 0.422044771
z Critical two-tail 1.959963985
Null hypothesis Regional mean price-Capital mean price =0
Alternative hypothesis Regional mean price-Capital mean price not equal to 0
Observation Decision
Z-stat<Critical(two tail) Fail to reject null hypothesis
P-value(PZ<=z) two tail > 0.05
Appendix C2: Question 2 Simple Linear Regression Model
Hypothesis 2: Is the relationship between diesel and Unleaded fuel prices linear of non-linear?

Running Head: Statistics
Chart 1: Scatter plot to identify the relationship between diesel and unleaded fuel prices
140.0 145.0 150.0 155.0 160.0 165.0 170.0
120.0
140.0
160.0
180.0
DIESEL AGAINST UNLEADED FUEL IN WESTERN
AUSTRALIA
Unleaded Fuel(Cent Per Litre)
Diesel(Cents Per Litre)
Table 2: Regression Analysis of data of price of diesel and unleaded fuels
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.88097241
5
R Square 0.77611239
7
Adjusted R Square 0.77324204
3
Standard Error 2.36423579
9
Observations 80
ANOVA
df SS MS F Significance
F
Regression 1 1511.369849 1511.3698
5
270.38909
7
4.562E-27
Residual 78 435.9896513 5.5896109
1
Total 79 1947.3595
Coefficients Standard
Error
t Stat P-value Lower 95% Upper 95%
Intercept 31.4241938
8
7.624810725 4.1213080
6
9.3167E-05 16.2443618 46.604026
Unleaded 91 (Cents per
Litre)
0.80591917
6
0.049011377 16.443512
3
4.562E-27 0.70834502 0.9034933
3
Chart 1: Scatter plot to identify the relationship between diesel and unleaded fuel prices
140.0 145.0 150.0 155.0 160.0 165.0 170.0
120.0
140.0
160.0
180.0
DIESEL AGAINST UNLEADED FUEL IN WESTERN
AUSTRALIA
Unleaded Fuel(Cent Per Litre)
Diesel(Cents Per Litre)
Table 2: Regression Analysis of data of price of diesel and unleaded fuels
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.88097241
5
R Square 0.77611239
7
Adjusted R Square 0.77324204
3
Standard Error 2.36423579
9
Observations 80
ANOVA
df SS MS F Significance
F
Regression 1 1511.369849 1511.3698
5
270.38909
7
4.562E-27
Residual 78 435.9896513 5.5896109
1
Total 79 1947.3595
Coefficients Standard
Error
t Stat P-value Lower 95% Upper 95%
Intercept 31.4241938
8
7.624810725 4.1213080
6
9.3167E-05 16.2443618 46.604026
Unleaded 91 (Cents per
Litre)
0.80591917
6
0.049011377 16.443512
3
4.562E-27 0.70834502 0.9034933
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Running Head: Statistics
Appendix C3: Multiple Linear Regression Model
Hypothesis 3: Does location influences the relationship between Unleaded 91 and Diesel prices?
Table 3: Regression Analysis for diesel price, Location and unleaded fuels price
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.88107394
R Square 0.77629129
Adjusted R Square 0.77048068
Standard Error 2.37858758
Observations 80
ANOVA
df SS MS F Significanc
e F
Regression 2 1511.71823 755.859113 133.598801 9.1789E-26
Residual 77 435.641274 5.65767888
Total 79 1947.3595
Coefficients Standard
Error
t Stat P-value Lower 95% Upper 95%
Intercept 31.5343268 7.68392453 4.103935 0.00010012 16.2336783 46.8349753
Location 0.13257776 0.5342749 0.24814522 0.80468263 -0.9312995 1.19645501
Unleaded 91 (Cents
per Litre)
0.80479513 0.04951652 16.2530629 1.3248E-26 0.70619514 0.90339512
Appendix C3: Multiple Linear Regression Model
Hypothesis 3: Does location influences the relationship between Unleaded 91 and Diesel prices?
Table 3: Regression Analysis for diesel price, Location and unleaded fuels price
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.88107394
R Square 0.77629129
Adjusted R Square 0.77048068
Standard Error 2.37858758
Observations 80
ANOVA
df SS MS F Significanc
e F
Regression 2 1511.71823 755.859113 133.598801 9.1789E-26
Residual 77 435.641274 5.65767888
Total 79 1947.3595
Coefficients Standard
Error
t Stat P-value Lower 95% Upper 95%
Intercept 31.5343268 7.68392453 4.103935 0.00010012 16.2336783 46.8349753
Location 0.13257776 0.5342749 0.24814522 0.80468263 -0.9312995 1.19645501
Unleaded 91 (Cents
per Litre)
0.80479513 0.04951652 16.2530629 1.3248E-26 0.70619514 0.90339512
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





