Statistical Analysis and Comparison between Stock Prices of Boeing Company and General Dynamics

This document provides a statistical analysis and comparison between the stock prices of Boeing Company and General Dynamics. The analysis includes volatility and market returns assessment, risk and average return relationship analysis, and hypothesis testing to compare average market returns and market risks.

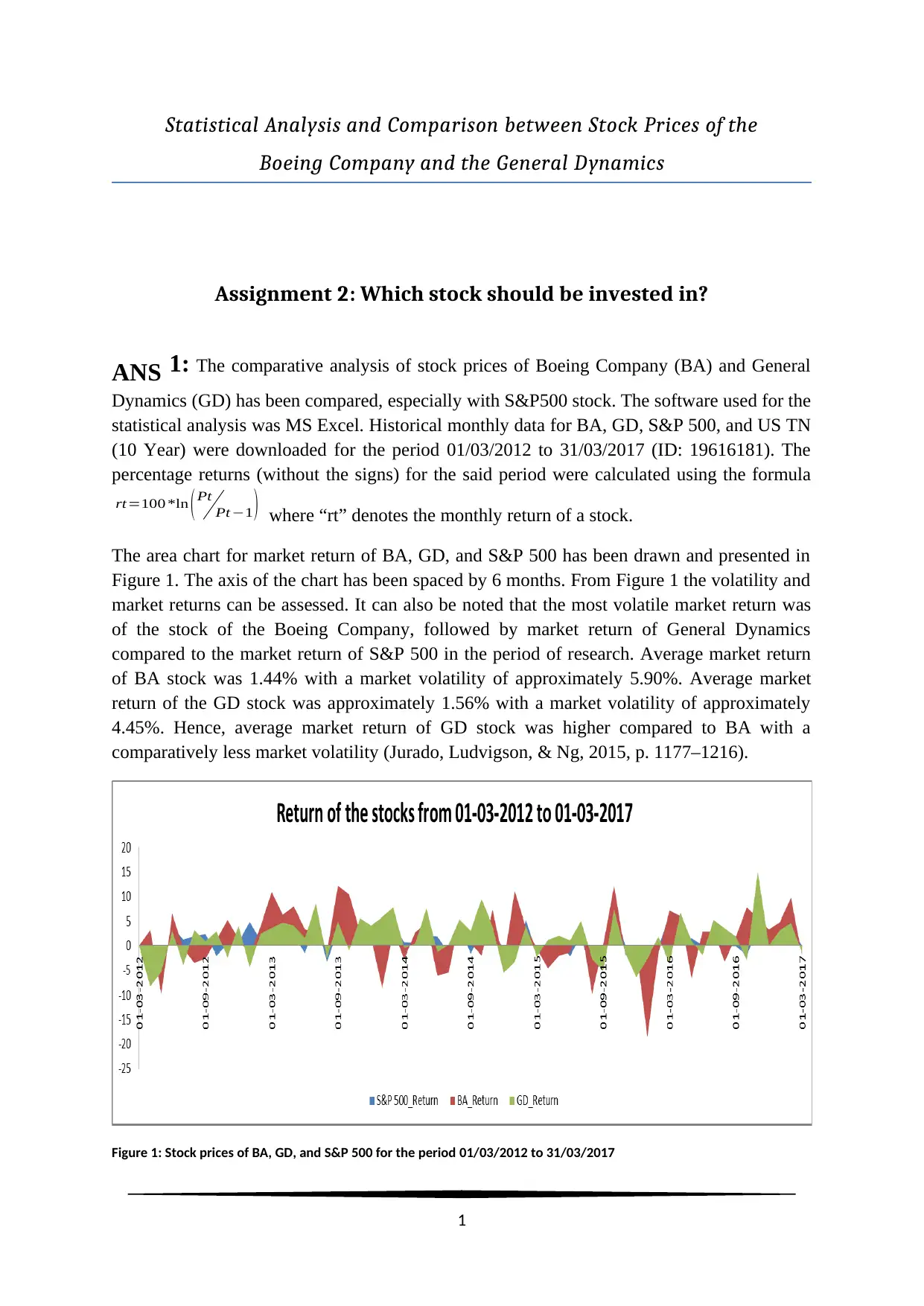
Statistical Analysis and Comparison between Stock Prices of the
Boeing Company and the General Dynamics
Assignment 2: Which stock should be invested in?
ANS 1: The comparative analysis of stock prices of Boeing Company (BA) and General
Dynamics (GD) has been compared, especially with S&P500 stock. The software used for the
statistical analysis was MS Excel. Historical monthly data for BA, GD, S&P 500, and US TN
(10 Year) were downloaded for the period 01/03/2012 to 31/03/2017 (ID: 19616181). The
percentage returns (without the signs) for the said period were calculated using the formula
rt=100 *ln ( Pt
Pt −1 ) where “rt” denotes the monthly return of a stock.
The area chart for market return of BA, GD, and S&P 500 has been drawn and presented in
Figure 1. The axis of the chart has been spaced by 6 months. From Figure 1 the volatility and
market returns can be assessed. It can also be noted that the most volatile market return was
of the stock of the Boeing Company, followed by market return of General Dynamics
compared to the market return of S&P 500 in the period of research. Average market return
of BA stock was 1.44% with a market volatility of approximately 5.90%. Average market
return of the GD stock was approximately 1.56% with a market volatility of approximately
4.45%. Hence, average market return of GD stock was higher compared to BA with a
comparatively less market volatility (Jurado, Ludvigson, & Ng, 2015, p. 1177–1216).
Figure 1: Stock prices of BA, GD, and S&P 500 for the period 01/03/2012 to 31/03/2017
1

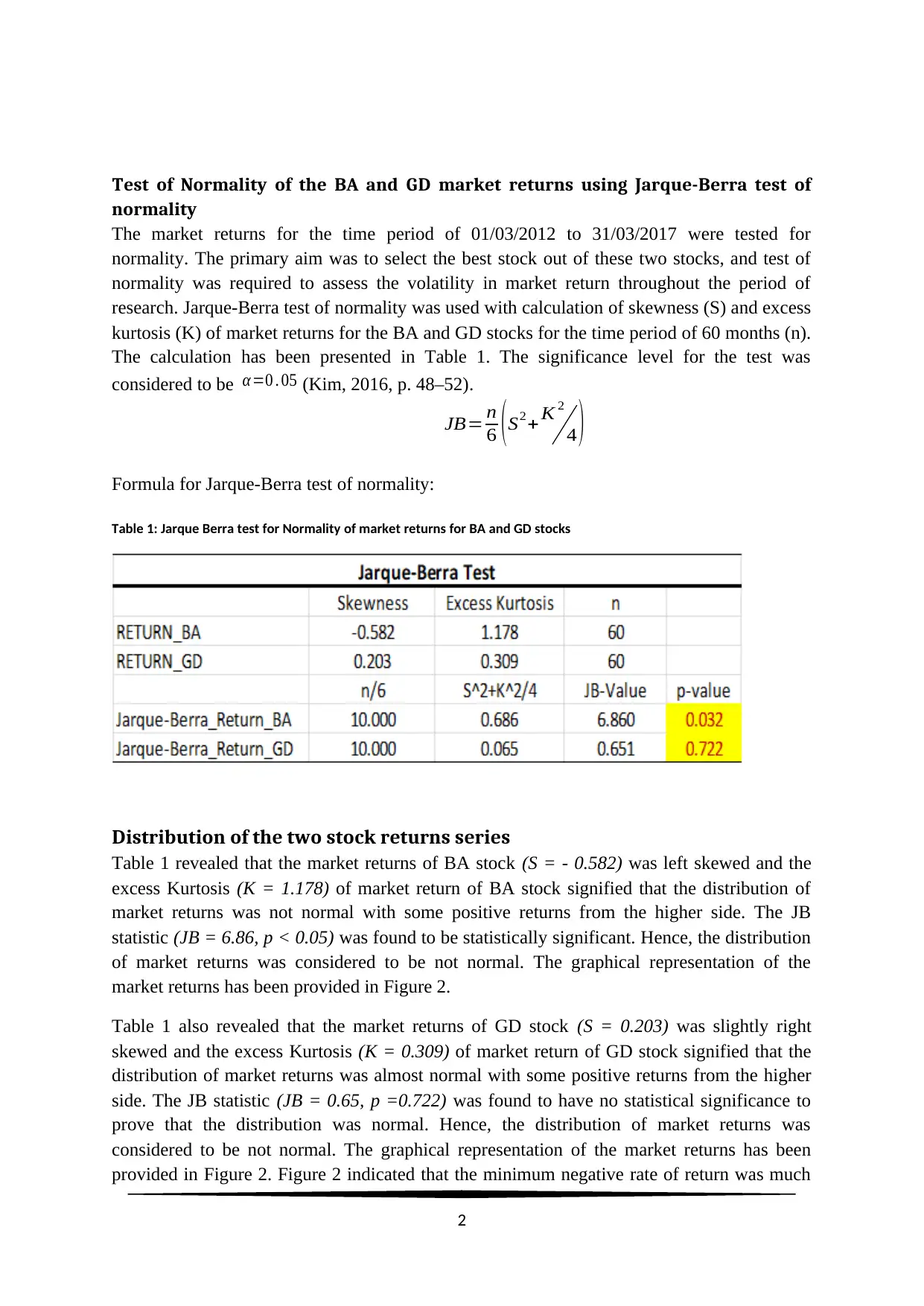
Test of Normality of the BA and GD market returns using Jarque-Berra test of
normality
The market returns for the time period of 01/03/2012 to 31/03/2017 were tested for
normality. The primary aim was to select the best stock out of these two stocks, and test of
normality was required to assess the volatility in market return throughout the period of
research. Jarque-Berra test of normality was used with calculation of skewness (S) and excess
kurtosis (K) of market returns for the BA and GD stocks for the time period of 60 months (n).
The calculation has been presented in Table 1. The significance level for the test was
considered to be α =0 . 05 (Kim, 2016, p. 48–52).
Formula for Jarque-Berra test of normality:
JB= n
6 ( S2+ K 2
4 )
Table 1: Jarque Berra test for Normality of market returns for BA and GD stocks
Distribution of the two stock returns series
Table 1 revealed that the market returns of BA stock (S = - 0.582) was left skewed and the
excess Kurtosis (K = 1.178) of market return of BA stock signified that the distribution of
market returns was not normal with some positive returns from the higher side. The JB
statistic (JB = 6.86, p < 0.05) was found to be statistically significant. Hence, the distribution
of market returns was considered to be not normal. The graphical representation of the
market returns has been provided in Figure 2.
Table 1 also revealed that the market returns of GD stock (S = 0.203) was slightly right
skewed and the excess Kurtosis (K = 0.309) of market return of GD stock signified that the
distribution of market returns was almost normal with some positive returns from the higher
side. The JB statistic (JB = 0.65, p =0.722) was found to have no statistical significance to
prove that the distribution was normal. Hence, the distribution of market returns was
considered to be not normal. The graphical representation of the market returns has been
provided in Figure 2. Figure 2 indicated that the minimum negative rate of return was much
2

higher for BA stock, whereas GD gave positive return maximum better compared to BA
stock.
Figure 2: Histogram of market returns of BA and GD stocks
Risk and Average Return Relationship
The comparison of market returns of GD and BA stocks with respect to their statistical
distributions was also analysed by the risk and average return relationship. The comparative
analysis has been presented in Table 2.
Table 2: Risk-Return relationship of market returns of GD and BA stocks
Table 2 revealed that average market return of the stock of Boeing Company was the
preeminent compared to the stocks of General Dynamic and S&P500. Investment in this
stock looked very lucrative considering the average return in the time period of 01/03/2012 to
31/03/2017. But the risk analysis revealed that volatility due to presence of few high market
returns as well as few extreme low return up to -18.53% was the greatest among the three
stocks. High market volatility always creates uncertainty in the mind of investor. Those who
like to take risk for higher returns may opt for the Boeing Company stock. But, considering
the higher average return and comparative low market risk stock of the General Dynamic was
the prudent choice as an investor. The coefficient of variation for all the three stocks were
calculated as statistical measure between average return and market risk. Ranking the funds
based on coefficient of variation revealed that BA was the most risky stock, followed by
S&P500. GD stock was the least risky to invest with a risk profile better than risk profile of
BA and the overall market scenario (Read, & Vogel, 2015, p. 6381–6398).
3

ANS 2: Reason and Choice of the test statistic to perform hypothesis testing:
Choice for the test statistic was based on the distribution and information about the
population and the sample data. The sample of calculated market returns for the period
01/03/2012 to 31/03/2017 in case of the GD stock was large enough (n >30) to assume that
the market returns would follow a standard normal distribution ( N ~ ( 0,1 ) ) . The argument
behind the assumption was obtained from Central Limit Theorem (CLT). Again, information
about the population regarding the market risk and average return were not available for the
research. Hence, a student’s t-distribution with 59 degrees of freedom was considered as the
appropriate choice as the test statistic.
To test the hypothesis that whether the average market return of the GD stock is different
from μ= 2.8% or not, a hypothesis testing for one-sample mean at 5% level of significance
was conducted.
I. Null hypothesis: H 0: ( μ=2 .8 ) was tested against the two tailed Alternate hypothesis
H A : ( μ≠2 . 8 ) .
II. Significance level of the test was considered to be at α=0 . 05 or 5%.
III. The average return of the GD stock for the period 01/03/2012 to 31/03/2017 was
considered normally distributed and the test statistic was calculated.
IV. Here, x
¿
=∑ xi
n =93 .653
60 =1 .561 and the risk or standard deviation was calculated as
s= √ ∑ ( xi−x
¿
)
2
n =4 . 454 .
The test statistic was
t= x
¿
−μ
s / √ n ~ N ( 0,1 ) and the statistic was calculated as,
t obs= x
¿
−μ
s / √ n =1 .561−2. 8
4 . 454 / √ 60 =−1 .239
0 .575 =−2. 155
Now critical value of the t-statistic at 5% level of significance for two tailed test is
t crit =1. 96 at 59 degrees of freedom. It was observed that tobs=−2 .155< tcrit =−1 . 96
on the left tail at 5% level. The value of the observed or calculated t-value falls in the
critical region in the left tail. The significance value or p-value was evaluated as p-
value = P ( t<−tobs ) + P¿ ¿
V. Hence, based on the statistical evidence the null hypothesis was rejected and it was
concluded that the average market return from GD stock was considerably different
4

from 2.8%, and the average actual market return of 1.56% was much lower than the
limit of 2.8%.
The MS Excel results for one sample t-test was compared and presented in Table 3 below.
Table 3: One sample t-test output
ANS 3: It was very essential to compare the risks involved while investing in the two
stocks. The descriptive details of both the stocks have been discussed earlier in detail analysis
of the stocks in answer 1. From the descriptive analysis GD stock was noted to have the least
risky profile. But the statistical significance of their difference, especially with respect to the
market risks would help investors to conclude on the choice of the stocks. A hypothesis was
tested to check whether risks involved in investing in the two stocks were statistically
different or not.
I. Null hypothesis H 0: ( σ1
2=σ2
2 ) was tested against a two tailed Alternate hypothesis
H A : ( σ1
2≠σ2
2 ) .
II. The level of significance for the test was chosen to be at 5% ( α=0 . 05 ) .
III. The risk or standard deviation of market returns for the BA stock was considered as
s1 and standard deviation of market returns for the GD stock was considered as s2 .
IV. Now, s12=34 . 853 and s22=19 . 841 from the descriptive details as well as the MS
Excel descriptive summary for market return of the two stocks. The test statistic was
calculated as
F= s1
2
s2
2 =34 . 853
19 .841 =1 . 7566
at 59 degrees of freedom.
The critical values for left tail and right tail for the F-test were evaluated as Fl . crit=0. 6 and
Fr . crit =1 .67 at 5% level of significance where degrees of freedom = 59.
5

The significance value or p-value was calculated as p=P ( F>1 . 7566 ) =0 . 0323<0 . 05
V. The p-value was less than the level of significance, which indicated that there was
enough statistical evidence to conclude that risk of investment in BA stock was
statistically significant and greater than that of the GD stock. Therefore, it was
possible to conclude that GD stock was much less riskier stock in the time period of
01/03/2012 to 31/03/2017. The MS Excel output and result for the F-test has been
presented in Table 4.
Table 4: F-test for comparison of market risks for GDS and BA stocks
ANS 4: After risk comparison both the stocks were compared for their average return in
the period of consideration. Descriptive analysis revealed that average return of the GD stock
was greater than that of the BA stock. Now, that observation has to be statistically tested, and
here the scholar tested whether average market returns from both the stocks were same or
significantly different (Lakens, 2017, p. 355–362).
I. Null hypothesis H 0: ( μBA−μGD ) was tested against the two tailed Alternate
hypothesis HA : ( μBA≠μGD ) .
II. The test was performed at 5% level of significance ( α=0 . 05 ) .
III. The sample observation for both the stocks were greater than 30, and using CLT
market returns of both the distributions were considered to be normal. Hence, choice
of test statistic at 118 degrees of freedom was considered to be t-statistic, and it is
defined as follows.
t = ( x
¿
BA −x
¿
GD )− ( μBA−μGD )
√ s1
2
n1
+ s2
2
n2
6

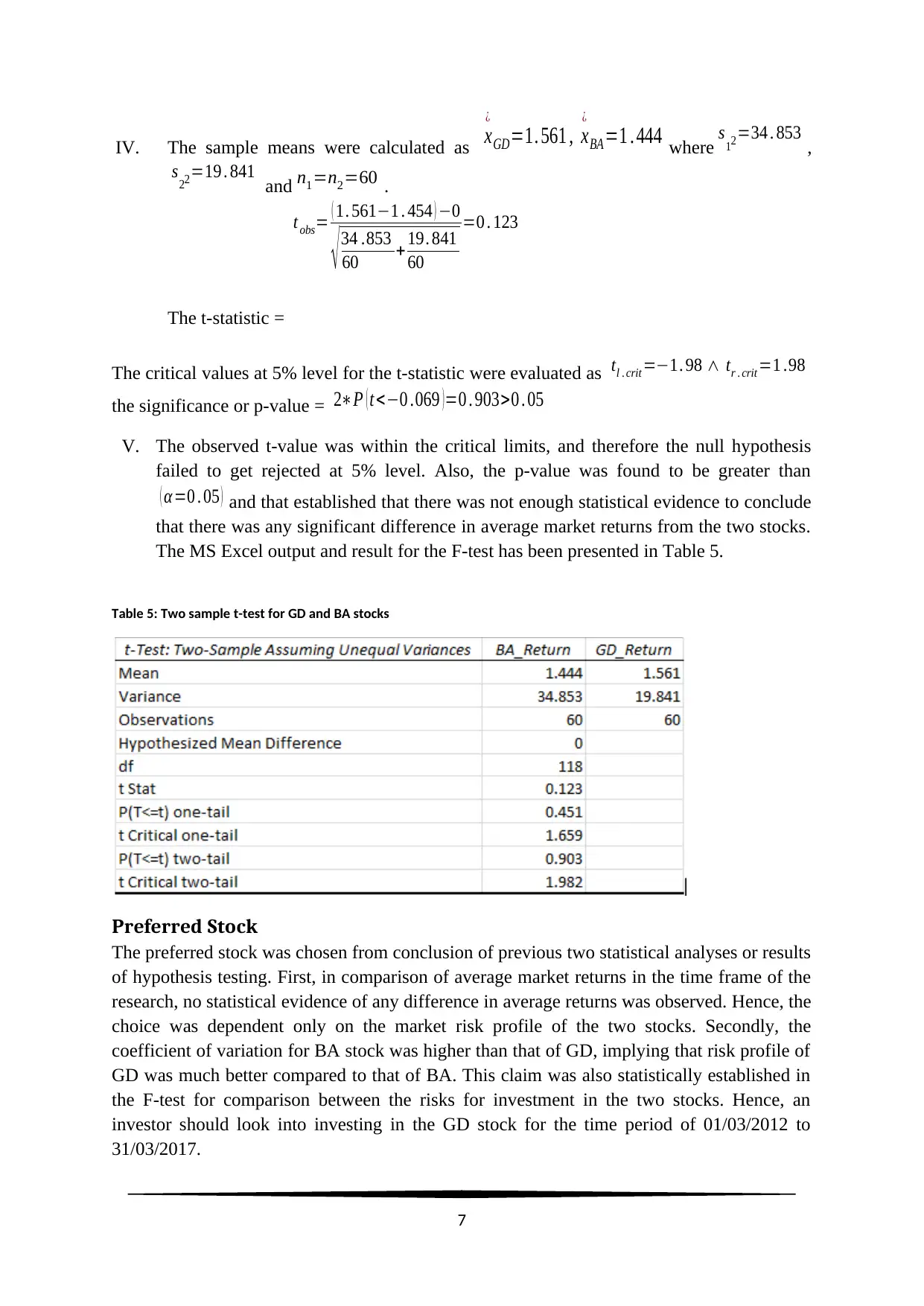
IV. The sample means were calculated as x
¿
GD=1. 561 , x
¿
BA =1 . 444 where s12=34 . 853 ,
s22=19 . 841 and n1=n2=60 .
The t-statistic =
tobs= ( 1. 561−1 . 454 ) −0
√ 34 .853
60 + 19. 841
60
=0 . 123
The critical values at 5% level for the t-statistic were evaluated as tl . crit =−1. 98 ∧ tr . crit =1 .98
the significance or p-value = 2∗P ( t<−0 .069 ) =0 . 903>0 . 05
V. The observed t-value was within the critical limits, and therefore the null hypothesis
failed to get rejected at 5% level. Also, the p-value was found to be greater than
( α=0 . 05 ) and that established that there was not enough statistical evidence to conclude
that there was any significant difference in average market returns from the two stocks.
The MS Excel output and result for the F-test has been presented in Table 5.
Table 5: Two sample t-test for GD and BA stocks
Preferred Stock
The preferred stock was chosen from conclusion of previous two statistical analyses or results
of hypothesis testing. First, in comparison of average market returns in the time frame of the
research, no statistical evidence of any difference in average returns was observed. Hence, the
choice was dependent only on the market risk profile of the two stocks. Secondly, the
coefficient of variation for BA stock was higher than that of GD, implying that risk profile of
GD was much better compared to that of BA. This claim was also statistically established in
the F-test for comparison between the risks for investment in the two stocks. Hence, an
investor should look into investing in the GD stock for the time period of 01/03/2012 to
31/03/2017.
7

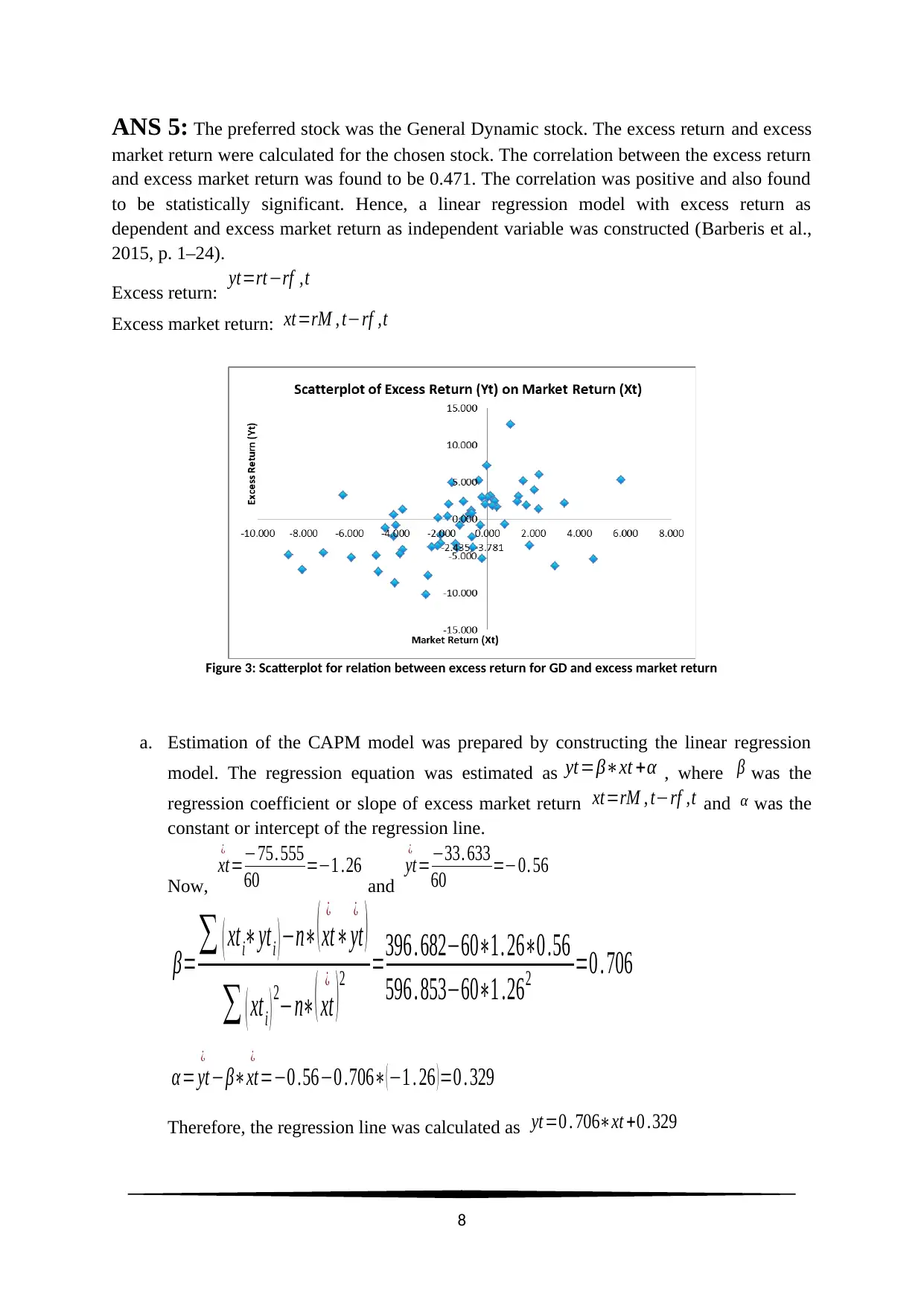
ANS 5: The preferred stock was the General Dynamic stock. The excess return and excess
market return were calculated for the chosen stock. The correlation between the excess return
and excess market return was found to be 0.471. The correlation was positive and also found
to be statistically significant. Hence, a linear regression model with excess return as
dependent and excess market return as independent variable was constructed (Barberis et al.,
2015, p. 1–24).
Excess return: yt=rt−rf ,t
Excess market return: xt=rM , t−rf ,t
Figure 3: Scatterplot for relation between excess return for GD and excess market return
a. Estimation of the CAPM model was prepared by constructing the linear regression
model. The regression equation was estimated as yt=β∗xt +α , where β was the
regression coefficient or slope of excess market return xt=rM , t−rf ,t and α was the
constant or intercept of the regression line.
Now,
xt
¿
=−75. 555
60 =−1 .26 and
yt
¿
=−33. 633
60 =−0. 56
β=∑ ( xti∗yti ) −n∗( xt
¿
∗yt
¿
)
∑ ( xti ) 2−n∗( xt
¿
) 2 =396 . 682−60∗1. 26∗0 .56
596 . 853−60∗1 .262 =0 . 706
α = yt
¿
−β∗xt
¿
=−0 .56−0 .706∗( −1 . 26 ) =0 . 329
Therefore, the regression line was calculated as yt=0 . 706∗xt +0 .329
8

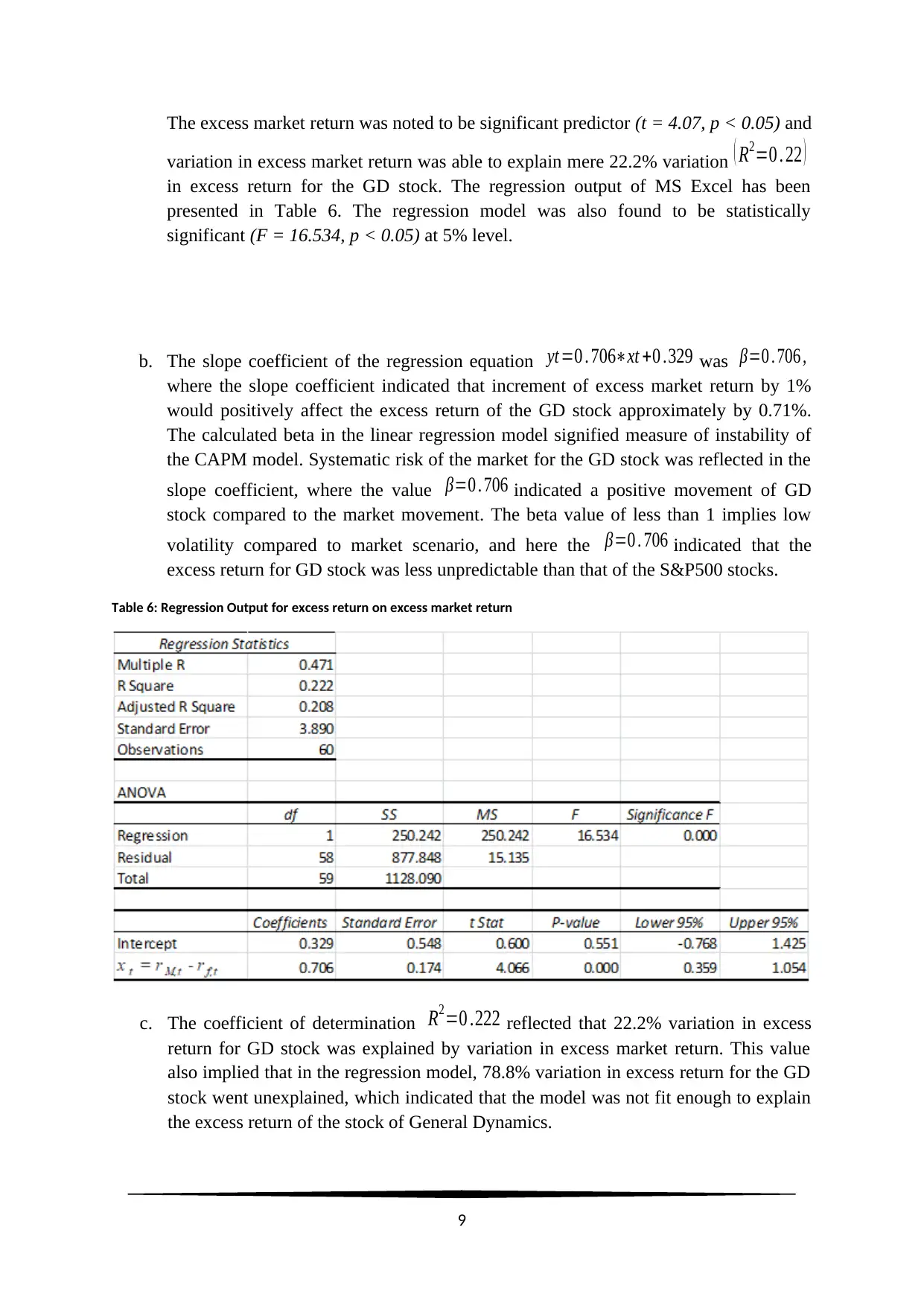
The excess market return was noted to be significant predictor (t = 4.07, p < 0.05) and
variation in excess market return was able to explain mere 22.2% variation ( R2=0 . 22 )
in excess return for the GD stock. The regression output of MS Excel has been
presented in Table 6. The regression model was also found to be statistically
significant (F = 16.534, p < 0.05) at 5% level.
b. The slope coefficient of the regression equation yt =0 . 706∗xt +0 .329 was β=0 . 706 ,
where the slope coefficient indicated that increment of excess market return by 1%
would positively affect the excess return of the GD stock approximately by 0.71%.
The calculated beta in the linear regression model signified measure of instability of
the CAPM model. Systematic risk of the market for the GD stock was reflected in the
slope coefficient, where the value β=0 . 706 indicated a positive movement of GD
stock compared to the market movement. The beta value of less than 1 implies low
volatility compared to market scenario, and here the β=0 . 706 indicated that the
excess return for GD stock was less unpredictable than that of the S&P500 stocks.
Table 6: Regression Output for excess return on excess market return
c. The coefficient of determination R2=0 .222 reflected that 22.2% variation in excess
return for GD stock was explained by variation in excess market return. This value
also implied that in the regression model, 78.8% variation in excess return for the GD
stock went unexplained, which indicated that the model was not fit enough to explain
the excess return of the stock of General Dynamics.
9

d. The 95% confidence interval for the slope coefficient was calculated as
[ β
^¿±tcrit∗SE ]=[0 . 706±2 .0∗0 .174 ]=[ 0 .358 ,1 .054 ]
¿ . With 95% confidence it was
possible to surmise that slope coefficient of excess return for the GD stock would be
somewhere between 0.358 and 1.054. Therefore, it was possible to conclude that for
1% change in excess market return would impact the excess return of the GD stock
approximately by 0.36% to 1.05%. This reflected that GD stock was less volatile
compared to the market or at maximum volatile approximately at par with the market
returns.
ANS 6: In language of economics, a Neutral stock varies parallel with the overall market
(Bali, Hu, & Murray, 2017, p.1-5). In statistical language Neutral stock implies that the beta
of the regression model would be equal to 1. The risk profile of Neutral stock is same as that
of the market (S&P500). Now to test whether GD was a Neutral stock, a hypothesis testing
with a one-sample t-test was performed at 5% level of significance.
I. Null hypothesis H 0: ( β =1 ) was tested against a two tailed Alternate hypothesis
HA : ( β≠1 ) .
II. Significance level for the test was considered to be at α =5 % or 0 .05
III. The test statistic was considered as
t= β
^¿− β0
se ¿ ¿ ¿ ¿ ¿
IV. The calculated value of the statistic was t= 0. 706−1
0 . 1737 =−1. 691 at 58 degrees of
freedom. The significance or p-value was calculated as
p=2∗P (|t|>1 .691 ) =0 .096 >0 . 05
The 95% confidence interval was calculated as,
[ β
^¿±tcrit∗SE ]=[0 . 706±2 .0∗0 .174 ]=[ 0 .358 ,1 .054 ]
¿
V. As the p-value was greater than the level of significance ( α=0 . 05 ) , there was not
enough statistical evidence to reject the null hypothesis at 5% level of significance.
Also, the hypothetical value of the slope coefficient was found to be within the 95%
confidence interval. Hence, with 95% confidence it was possible to infer that the
estimated slope coefficient for the regression model will be approximately somewhere
within 0.358 and 1.054. Therefore, the null hypothesis could not be rejected and it
was concluded that the GD stock undeniably was a Neutral stock.
10

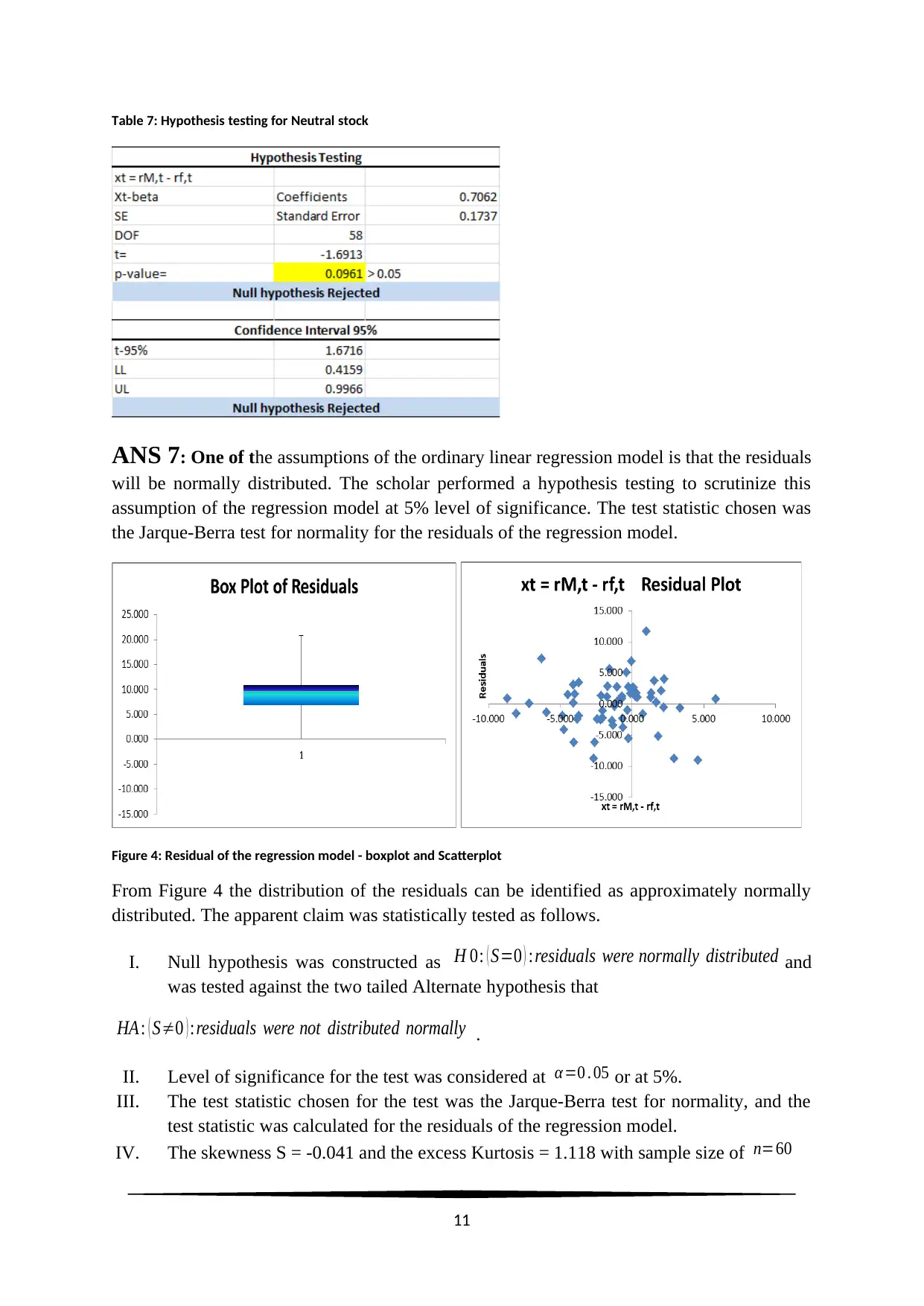
Table 7: Hypothesis testing for Neutral stock
ANS 7: One of the assumptions of the ordinary linear regression model is that the residuals
will be normally distributed. The scholar performed a hypothesis testing to scrutinize this
assumption of the regression model at 5% level of significance. The test statistic chosen was
the Jarque-Berra test for normality for the residuals of the regression model.
Figure 4: Residual of the regression model - boxplot and Scatterplot
From Figure 4 the distribution of the residuals can be identified as approximately normally
distributed. The apparent claim was statistically tested as follows.
I. Null hypothesis was constructed as H 0: ( S=0 ) :residuals were normally distributed and
was tested against the two tailed Alternate hypothesis that
HA : ( S≠0 ) : residuals were not distributed normally .
II. Level of significance for the test was considered at α=0 . 05 or at 5%.
III. The test statistic chosen for the test was the Jarque-Berra test for normality, and the
test statistic was calculated for the residuals of the regression model.
IV. The skewness S = -0.041 and the excess Kurtosis = 1.118 with sample size of n=60
11

The JB-statistic was calculated as JB= n
6 ( S2+ K 2
4 ) =3 .143 . The significance or the p-value
for the JB-statistic was calculated considering the fact that JB-statistic follows Chi-Square
distribution with 2 degrees of freedom. Hence, the p-value = CHIDIST (JB, 2) = CHIDIST
(3.143, 2) = 0.208 > 0.05.
V. Here the significance or the p-value was found to be greater than the level of
significance ( α=0 . 05 ) . Hence, there was not enough statistical evidence at 5% level to
reject the null hypothesis that assumed that the residuals were normally distributed
with skewness, S = 0. Hence, it was possible to conclude that the assumption of the
ordinary linear regression, that the residuals are normally distributed, stands out to be
plausible for the present regression model (Harrell, 2015, p. 359–387).
References
Bali, TG, Hu, J & Murray, S 2017, ‘Option implied volatility, skewness, and kurtosis and the
cross-section of expected stock returns’,.pp.1-5
Barberis, N, Greenwood, R, Jin, L & Shleifer, A 2015, ‘X-CAPM: An extrapolative capital
asset pricing model’, Journal of financial economics, vol. 115, no. 1, pp. 1–24.
Harrell, FE 2015, ‘Regression Models for Continuous Y and Case Study in Ordinal
Regression’, in Regression Modeling Strategies, Springer, pp. 359–387.
Jurado, K, Ludvigson, SC & Ng, S 2015, ‘Measuring Uncertainty’, American Economic
Review, vol. 105, no. 3, pp. 1177–1216.
Kim, N 2016, ‘A robustified Jarque–Bera test for multivariate normality’, Economics Letters,
vol. 140, pp. 48–52.
Lakens, D 2017, ‘Equivalence tests: a practical primer for t tests, correlations, and meta-
analyses’, Social Psychological and Personality Science, vol. 8, no. 4, pp. 355–362.
Read, LK & Vogel, RM 2015, ‘Reliability, return periods, and risk under nonstationarity’,
Water Resources Research, vol. 51, no. 8, pp. 6381–6398.
12