Statistics and Probability Questions 2022

Running head: Statistics and probability 1
Statistics and Probability
Course code
Student name
Tutor

Statistics and Probability 2
QUESTION 1
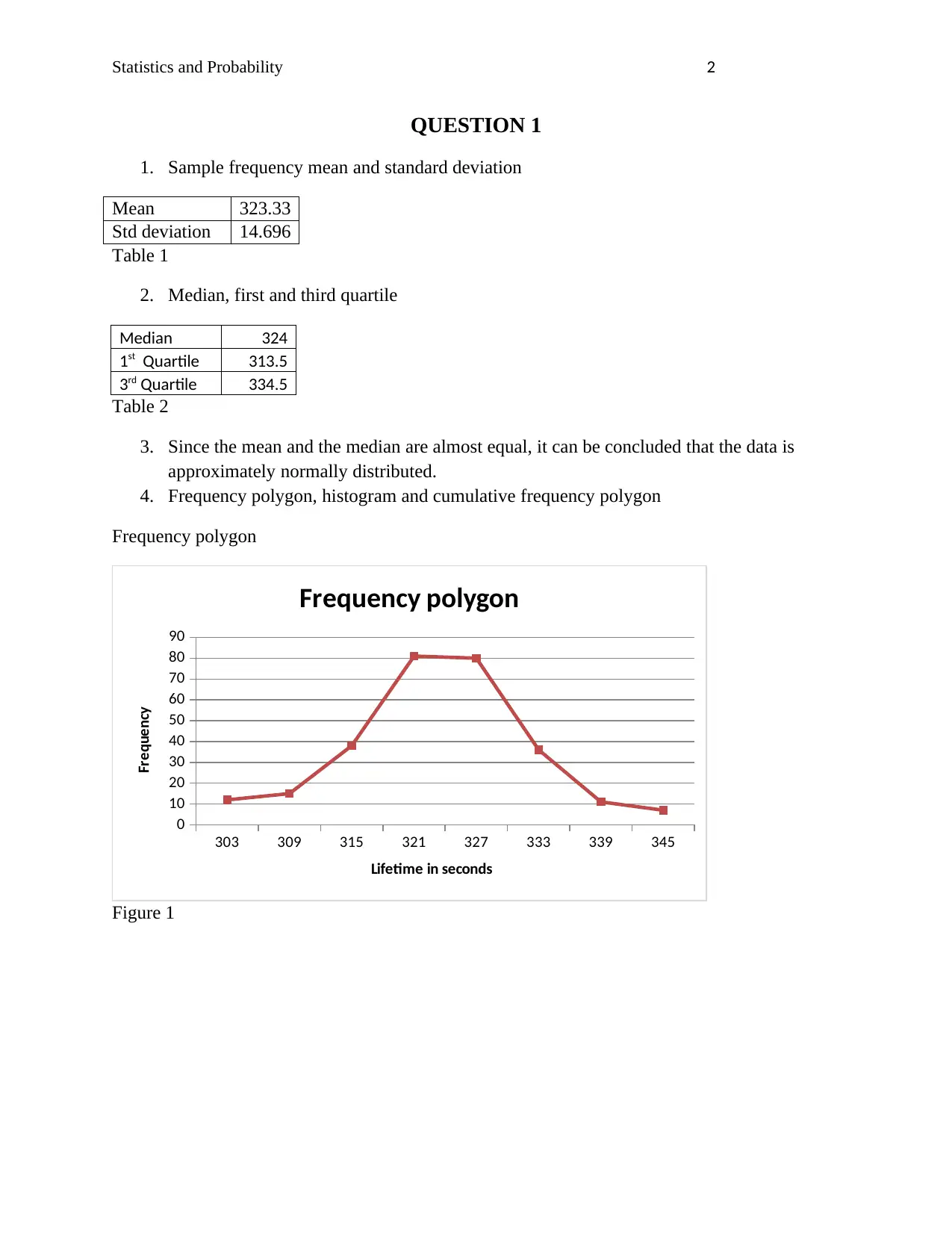
1. Sample frequency mean and standard deviation
Mean 323.33
Std deviation 14.696
Table 1
2. Median, first and third quartile
Median 324
1st Quartile 313.5
3rd Quartile 334.5
Table 2
3. Since the mean and the median are almost equal, it can be concluded that the data is
approximately normally distributed.
4. Frequency polygon, histogram and cumulative frequency polygon
Frequency polygon
303 309 315 321 327 333 339 345
0
10
20
30
40
50
60
70
80
90
Frequency polygon
Lifetime in seconds
Frequency
Figure 1

Statistics and Probability 3
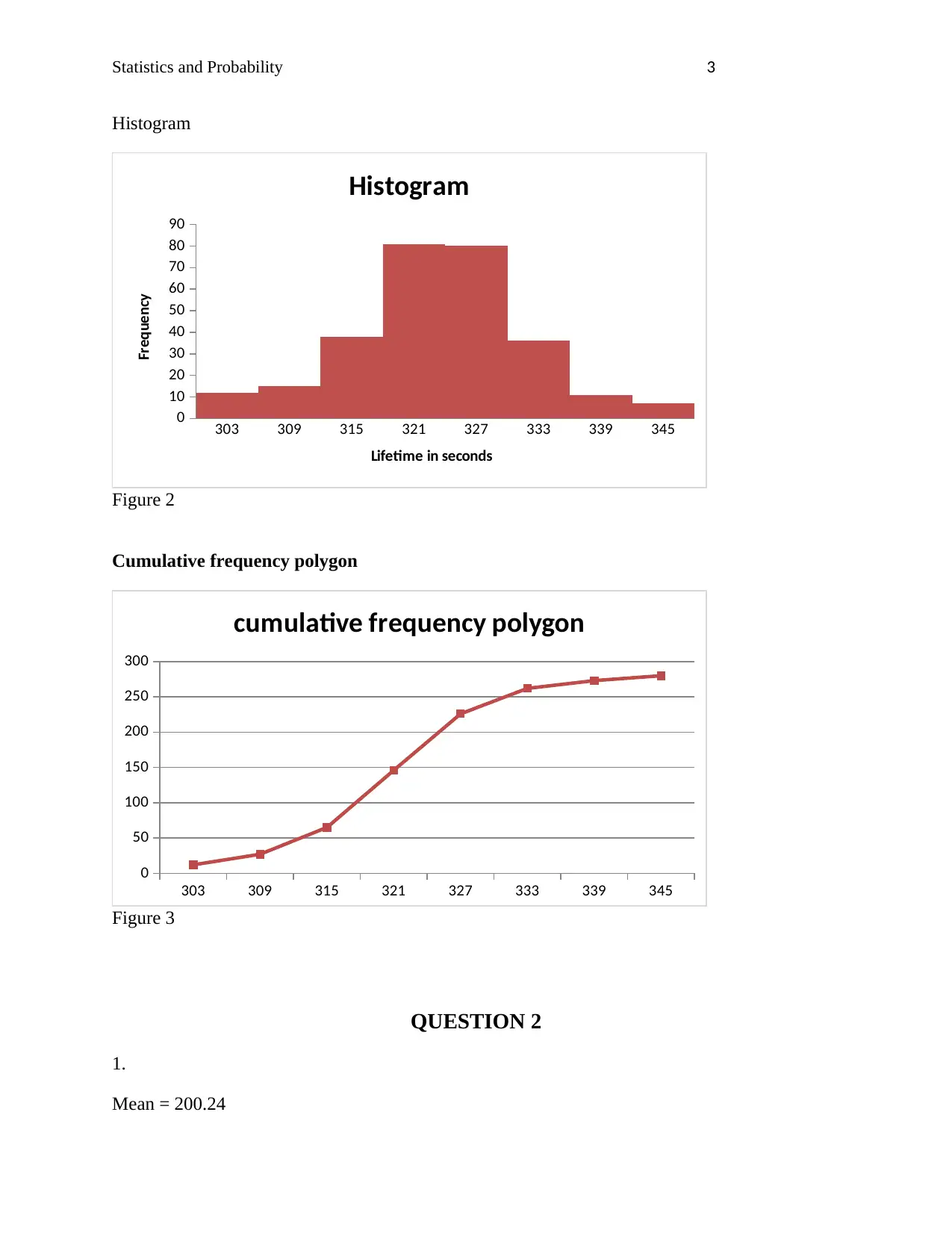
Histogram
303 309 315 321 327 333 339 345
0
10
20
30
40
50
60
70
80
90
Histogram
Lifetime in seconds
Frequency
Figure 2
Cumulative frequency polygon
303 309 315 321 327 333 339 345
0
50
100
150
200
250
300
cumulative frequency polygon
Figure 3
QUESTION 2
1.
Mean = 200.24

Statistics and Probability 4
Standard deviation = 3.75
X = 200
Z= x −μ
σ
Z=200.24−200
3.75 =0.064
P value corresponding to a Z-value of 0.064 for a two-tailed test at 0.05 level of significance is
0.94897
2. Hypothesis
H0: μ = 200
H1: μ ≠ 200
Alpha = 0.05
3. The structure of the test becomes a two-tailed test since the mean can either be greater or less
than 200 grams.
4. Since the p-value (0.95) is greater than the level of significance, the null hypothesis is not
rejected. It is concluded that the mean weight of the packets is 200 grams.
5.
Mean = 199.16
Standard deviation = 2.76
X = 200
Z= x −μ
σ
Z=5−2.76
3.75 =0.597
P value corresponding to a Z-value of 0.597 for a two-tailed test at 0.05 level of significance is
0.5505
6. Hypothesis

Statistics and Probability 5
H0: μ = 5
H1: μ ≠ 5
Alpha = 0.05
7. The structure of the test becomes a two-tailed test since the mean variance can either be
greater or less than 5 grams.
8. Since the p-value (0.55) is greater than the level of significance (0.05), the null hypothesis is
not rejected. It is concluded that the mean variance of the packets is 5 grams.
QUESTION 3
1. Hypothesis
Hypothesis
H0: There is no difference in the mean distance covered between the two teams
H1: There is a significant difference in the mean distance covered between the two teams
Alpha = 0.05
Independent sample t-test will be employed
2. Mean and standard deviation
List A
mean
1507.87
1
std deviation 43.044
Table 1
List B
mean
1487.12
4
Std deviation 27.5008
Table 2
3. The structure of my statistical test will adopt the use of sample t-test with unequal
variance since the variances of the two are very different.

Statistics and Probability 6
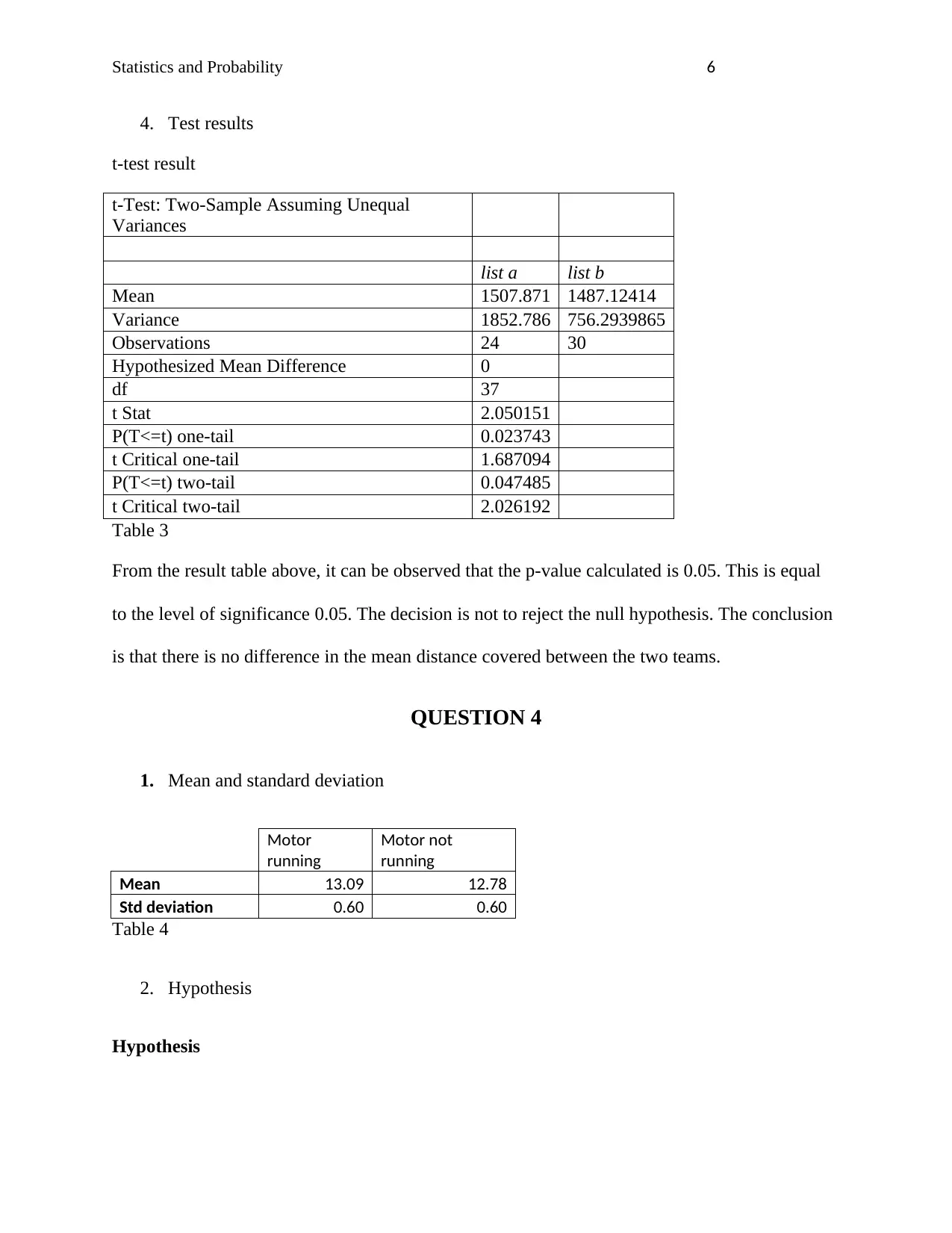
4. Test results
t-test result
t-Test: Two-Sample Assuming Unequal
Variances
list a list b
Mean 1507.871 1487.12414
Variance 1852.786 756.2939865
Observations 24 30
Hypothesized Mean Difference 0
df 37
t Stat 2.050151
P(T<=t) one-tail 0.023743
t Critical one-tail 1.687094
P(T<=t) two-tail 0.047485
t Critical two-tail 2.026192
Table 3
From the result table above, it can be observed that the p-value calculated is 0.05. This is equal
to the level of significance 0.05. The decision is not to reject the null hypothesis. The conclusion
is that there is no difference in the mean distance covered between the two teams.
QUESTION 4
1. Mean and standard deviation
Motor
running
Motor not
running
Mean 13.09 12.78
Std deviation 0.60 0.60
Table 4
2. Hypothesis
Hypothesis

Statistics and Probability 7
H0: There is no difference in the mean resistance between when the motor is running and when it
is not running.
H1: The mean resistance of the control circuit is lower when the machine motor is running
Alpha = 0.05
Independent sample t-test will be employed
3. This will be a paired sample t-test with equality in variance since the variances are equal.
It will also be a one-tailed test since the hypothesis is directional.
4. Statistical test
t-Test: Two-Sample Assuming Equal Variances
Motor running Motor not running
Mean 13.094 12.78140351
Variance 0.274277895 0.365378947
Observations 20 20
Pooled Variance 0.319828421
Hypothesized Mean Difference 0
df 38
t Stat 1.747936181
P(T<=t) one-tail 0.044275876
t Critical one-tail 1.68595446
P(T<=t) two-tail 0.088551752
t Critical two-tail 2.024394164
Table 5
From the result table above, it can be observed that the p-value calculated is 0.04. This is less
than the level of significance 0.05. The decision is to reject the null hypothesis. The conclusion is
that there is the mean resistance of the control circuit is lower when the machine motor is
running.

Statistics and Probability 8
QUESTION 5
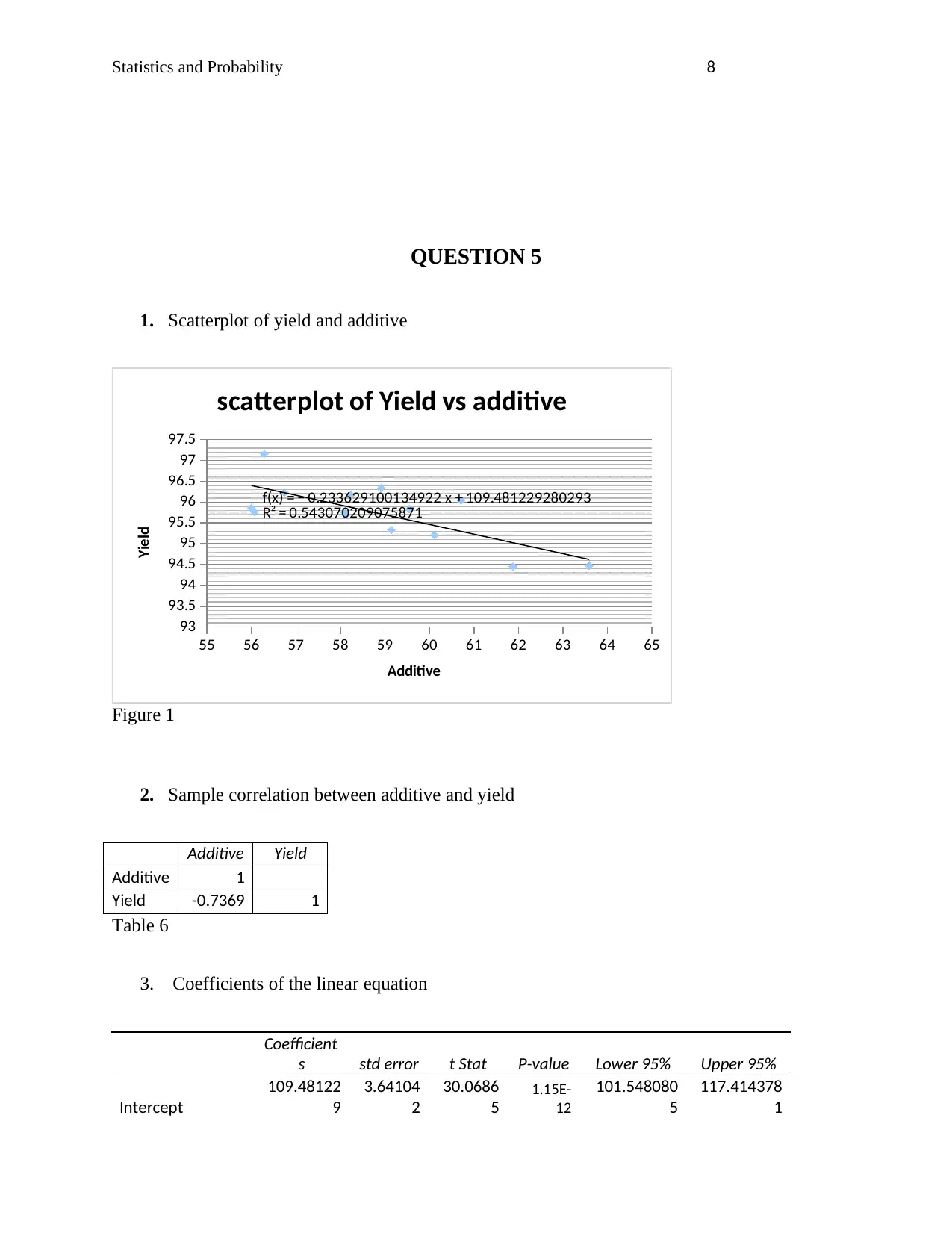
1. Scatterplot of yield and additive
55 56 57 58 59 60 61 62 63 64 65
93
93.5
94
94.5
95
95.5
96
96.5
97
97.5
f(x) = − 0.233629100134922 x + 109.481229280293
R² = 0.543070209075871
scatterplot of Yield vs additive
Additive
Yield
Figure 1
2. Sample correlation between additive and yield
Additive Yield
Additive 1
Yield -0.7369 1
Table 6
3. Coefficients of the linear equation
Coefficient
s std error t Stat P-value Lower 95% Upper 95%
Intercept
109.48122
9
3.64104
2
30.0686
5
1.15E-
12
101.548080
5
117.414378
1

Statistics and Probability 9
Additive -0.2336291
0.06186
3 -3.77654
0.0026
4 -0.36841764
-
0.09884055
Table 7
Yield=−0.23 ( Additive ) +109.5
4. Test
Hypothesis
H0: There is no relationship between amount of yield and additive.
H1: There is a significant relationship between amount of yield and additive.
Alpha = 0.05
5. If the p-value computed will be less than 0.05, the null hypothesis will be rejected and
that would mean that there is a significant relationship between yield and additive.
6. Results of the hypothesis
Correlations
Additive Yield
Additive
Pearson Correlation 1 -.737**
Sig. (2-tailed) .003
N 14 14
Yield
Pearson Correlation -.737** 1
Sig. (2-tailed) .003
N 14 14
**. Correlation is significant at the 0.01 level (2-tailed).
Table 8
From the Pearson result table above, it can be observed that the p-value calculated is 0.003. This
is less than the level of significance 0.05. The decision is to reject the null hypothesis. The
conclusion is that there is there is a significant relationship between amount of yield and
additive. However, the relationship is negative.

Statistics and Probability 10
7. The regression equation is fit for predicting the data since the value of F-significance is
0.00.
QUESTION 6
.
Hypothesis
H0: There is no association between the type of school and education outcome.
H1: There is a significant relationship between the type of school and education outcome.
Alpha = 0.05
This is a chi-square test of independence
Pearson Chi-Square = 2.645, DF = 8, P-Value = 0.955
Likelihood Ratio Chi-Square = 2.656, DF = 8, P-Value = 0.954
Since the p-value (0.955) is greater than the level of significance, the null hypothesis is not
rejected. It is concluded therefore that there is no association between the type of school and
education outcome.

Statistics and Probability 11