Detailed Report: Binary Arithmetic System, Algorithms, and Examples

This report provides a comprehensive analysis of the binary number system and its significance in computer science. It begins with an introduction to binary arithmetic, explaining its preference over other number systems due to its simplicity and efficiency in digital devices. The report explores the problem of converting human language to binary code for machine understanding, highlighting the role of the Arithmetic Logic Unit (ALU) and Central Processing Unit (CPU) in this process. It then details the benefits of using a binary arithmetic system, such as its widespread availability of resources and its fundamental role in electronic devices. The report presents algorithms and flowcharts for binary addition, subtraction, multiplication, and division, along with trace tables demonstrating these operations with example inputs. The conclusion emphasizes the importance of the binary number system in technological advancements, including its application in various fields like data security and software development, and the contribution of group members to the report. References to relevant literature are also provided.

Table of Contents
Introduction...........................................................................................................................................2
Problem Explanation.............................................................................................................................2
Benefits of Using Binary Arithmetic System..........................................................................................2
Application............................................................................................................................................2
Flowchart...............................................................................................................................................3
Algorithm:..............................................................................................................................................4
Test on Input-1......................................................................................................................................5
Trace Table -1....................................................................................................................................6
Test on Input-2......................................................................................................................................7
Trace Table -2....................................................................................................................................8
Conclusion...........................................................................................................................................10
Contribution of Group Member..........................................................................................................10
References...........................................................................................................................................10
Page 1 of 10

Introduction
This report analyses and mentions the importance of binary number system and its preference over
other number systems. The Binary number system comprises of only 1’s and 0’s. The main challenge
arises when neither the computer nor a human being can understand each other’s language and
hence the high-level language is converted to binary code. This task is basically carried out by the
ALU and the CPU. The user input data is split into small units. Further arithmetic operations on the
data are carried out. Binary operators like addition, Subtraction, Multiplication, and division split the
data into categories namely real number and imaginary numbers which are further useful for actual
period activities namely animation, image processing and many more.
Problem Explanation
A machine understands only the binary number system but on the contrary it is also true that a
machine is human instructed device and without an actual mediation between the human code and
a binary number system, the machine would be of no use to the mankind as there would be many
errors. Thus, after the conversion of human code to binary code, the processing of this binary code
by many binary arithmetic operators is needed. Thus, the binary number system is the base of any
machine and is important to run real time tasks on the machine.
Benefits of Using Binary Arithmetic System
The benefits of using a binary arithmetic number system are.
 Wide range of resources on the internet and library, which are easily accessible.
 As binary number system us widely used overall electronic devices, we can analyse its uses
and its importance by ourselves.
 It is one of the familiar topics, so information collection becomes easy and effective.
Application
A simple algorithm is developed which is used for adding two numbers. The flow chart of the
algorithm is provided below. A random variable is taken to store the carry. The addition of the
number goes on from right to left.
Page 2 of 10

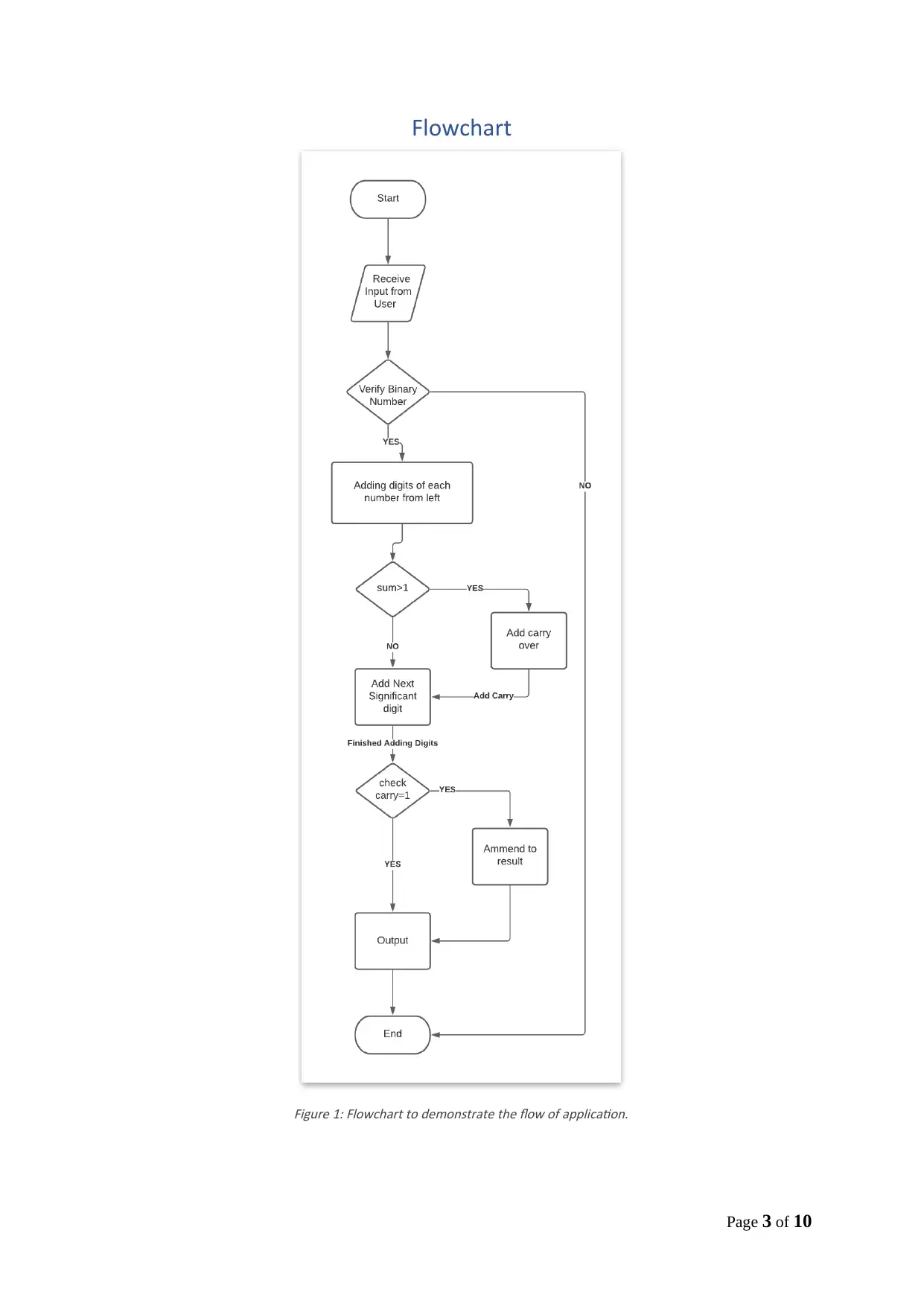
Flowchart
Figure 1: Flowchart to demonstrate the flow of application.
Page 3 of 10

Algorithm:
Binary Addition:
case A + B Sum Carry
1 0 + 0 0 0
2 0 + 1 1 0
3 1 + 0 1 0
4 1 + 1 0 1
In the 4th case, the binary addition of (1+1=10). So, 0 is written in the given column and a carry of 1
over to the next column.
1. Start
2. Take inputs in two numbers A and B from the user.
3. Add the digits from left to right.
i. If Sum > 1,
ii. Store the carry, and
4. If carry = 1
i. Add carry to next bit.
5. Repeat the above steps 3 and 4.
i. If there is no digit smaller number, then.
ii. Use 0 for it.
6. If the carry is greater than 0 (carry>0), then.
i. Append the result to the carry.
7. Display the Added number
8. End
Binary Subtraction:
A - B Subtract Borrow
0 - 0 0 0
0 - 1 1 1(borrow 1, resulting in -1 carried over)
1 - 0 1 0
1 - 1 0 0
1. Start
2. Take inputs in two numbers A and B from the user.
3. Subtract the digits from left to right.
i. If digit of first number = 0,
ii. Borrow = 10, and
4. If borrow = 10
i. Next bit = 0.
5. Repeat the above steps 3 and 4.
i. If there is no digit smaller number, then.
ii. Use 0 for it.
6. Display the subtracted number.
7. End
Page 4 of 10

Binary Multiplication:
A * B Multiplication
0 * 0 0
0 * 1 0
1 * 0 0
1 * 1 1
1. Start
2. Take inputs in two numbers A and B from the user.
3. Multiply every bit of B first with one bit of A (start the digits from left to right).
i. If both the bits are 1,
ii. Multiplication=1, and
4. Repeat the above step 3 until every bit of A is unreached.
i. Use the subtraction algorithm to subtract the digits of all levels.
5. Display the subtracted number (multiplies number)
6. End
Binary Division:
A ÷ B Division
0 ÷ 0 Meaningless
0 ÷ 1 0
1 ÷ 0 Meaningless
1 ÷ 1 1
1. Start
2. Take inputs in two numbers A and B from the user.
3. Divide B with the A (start the digits from right to left).
i. If both the bits are 1,
ii. Division=1, and
iii. If A=0 and B=1, then
iv. Division=0
v. Else, it is meaningless.
4. Repeat the above step 3 until every bit of A is unreached.
i. Use the subtraction algorithm to subtract the digits of all levels.
5. Display the division number as the output.
6. End
Test on Input-1
Binary Addition:
Step 1: Input numbers are 100 and 010.
Step 2: 0 + 0 = 0
Step 3: 0 + 1 = 1
Page 5 of 10

Step 4: 1 + 0 = 1
Step 5: The carry = 0, so the output is = 110
Trace Table -1
Steps Operation Answer Carry Output
1 - - - -
2 0+0 0 0 -
3 0+1 1 0 -
4 1+0 1 0 -
5 - - - 110
Binary Subtraction:
Step 1: Input numbers are 111 and 011.
Step 2: 1 - 1 = 0
Step 3: 1 - 1 = 0
Step 4: 1 - 0 = 1
Step 5: The output is = 100
Trace Table -1
Steps Operation Answer Borrow Output
1 - - - -
2 1-1 0 0 -
3 1-1 0 0 -
4 1-0 1 0 -
5 - - - 100
Binary Multiplication:
Step 1: Input numbers are 1000 and 11.
Step 2: 1000 * 1
Step 2.1: 0*1 = 0
Step 2.2: 0*1 = 0
Step 2.3: 0*1 = 0
Step 2.4: 1*1 = 1
Step 3: 1000 * 1
Step 3.1: 0*1 = 0
Step 3.2: 0*1 = 0
Step 3.3: 0*1 = 0
Step 3.4: 1*1 = 1
Step 5: Add 1000 + 1000x
Page 6 of 10

Step 6: The output is: 11000
Trace Table -1
Steps Operation Answer Output
1 - - -
2 1000*1 1000 -
3 1000*1 1000 -
4 1000+1000x - -
5 - - 11000
Binary Division:
Step 1: Input numbers are 1000 and 100.
Step 2: 100/100 = 1
Step 2.1: Remainder: 0
Step 3: 0 / 100 = 0
Step 3.1: Remainder: 0
Step 4: Append 1 with 0
Step 5: The output is: 10
Trace Table -1
Steps Operation Remainder Answer Output
1 - - - -
2 100/100 0 1 -
3 0/100 0 0 -
4 Append 1 with 0 - 10 -
5 - - - 10
Test on Input-2
Binary Addition:
Step 1: Input numbers are 1011 and 0101.
Step 2: 1 + 1 = 10
Step 2.1: Carry =1, so carry over
Step 3: 1 + 0 = 1
Step 3.1: 1 + 1(Carry) = 10
Step 3.2: Carry is 1, so carry over.
Step 4: 0 + 1 = 1
Step 4.1: 1 + 1(Carry) = 10
Step 4.2: Carry=1, so carry over
Page 7 of 10

Step 5: 1 + 0 = 1
Step 5.1: 1 + 1(Carry) = 10
Step 5.2: Carry is 1, so carry over.
Step 6: 1 carry over.
Step 6.1: 1 append to the result.
Step 7: Output = 10000
Step 8: End
Trace Table -2
Steps Operation Answer Carry Output
1 - - - -
2 1+1 0 1 -
2.1 - - 1 -
3 1+0 1 0 -
3.1 1+1(Carry) 0 1 -
4 0+1 1 0 -
4.1 1+1(Carry) 0 1 -
5 1+0 1 0 -
5.1 1+1(Carry) 0 1 -
6 - - 1 -
6.1 - - - -
7 - - - 10000
Binary Subtraction:
Step 1: Input numbers are 1010 and 0101.
Step 2: 0 – 1 = 1
Step 2.1: Borrow: 1
Step 3: 1+(-1)-0 = 0
Step 4: 0 – 1 = 1
Step 4.1: Borrow: 1
Step 3: 1+(-1)-0 = 0
Step 5: The output is = 0101
Trace Table -2
Steps Operation Answer Borrow Output
1 - - - -
2 0-1 1 1 -
3 1+(-1)-0 0 0 -
4 0-1 1 1 -
5 1+(-1)-0 0 0
6 - - - 0101
Page 8 of 10

Binary Multiplication:
Step 1: Input numbers are 1011 and 101.
Step 2: 1011 * 1
Step 2.1: 1*1 = 1
Step 2.2: 1*1 = 1
Step 2.3: 0*1 = 0
Step 2.4: 1*1 = 1
Step 3: 1011 * 0
Step 3.1: 1*0 = 0
Step 3.2: 1*0 = 0
Step 3.3: 0*0 = 0
Step 3.4: 1*0 = 0
Step 4: 1011 * 1
Step 4.1: 1*1 = 1
Step 4.2: 1*1 = 1
Step 4.3: 0*1 = 0
Step 4.4: 1*1 = 1
Step 5: Add 1011 + 0000x + 1011xx
Step 6: The output is: 110111
Trace Table -2
Steps Operation Answer Output
1 - - -
2 1011*1 1011 -
3 1011*0 0000 -
4 1011*1 1011 -
5 1011+0000x+1011xx - -
6 - - 110111
Binary Division:
Step 1: Input numbers are 101011 and 11.
Step 2: 101/11 = 1
Step 2.1: Remainder: 1
Step 3: 100/11 = 1
Step 3.1: Remainder: 1
Step 4: 11/11 = 1
Page 9 of 10

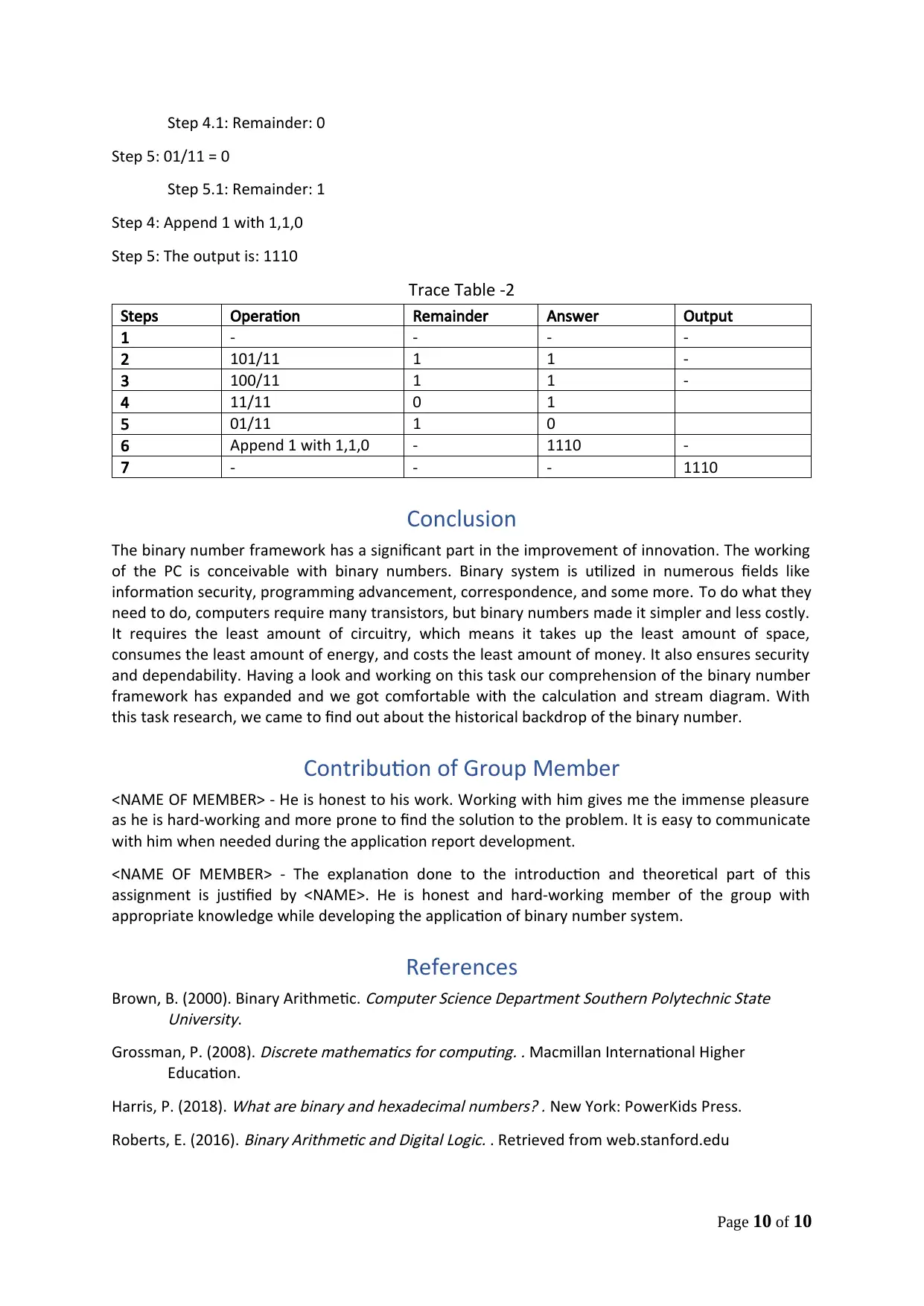
Step 4.1: Remainder: 0
Step 5: 01/11 = 0
Step 5.1: Remainder: 1
Step 4: Append 1 with 1,1,0
Step 5: The output is: 1110
Trace Table -2
Steps Operation Remainder Answer Output
1 - - - -
2 101/11 1 1 -
3 100/11 1 1 -
4 11/11 0 1
5 01/11 1 0
6 Append 1 with 1,1,0 - 1110 -
7 - - - 1110
Conclusion
The binary number framework has a significant part in the improvement of innovation. The working
of the PC is conceivable with binary numbers. Binary system is utilized in numerous fields like
information security, programming advancement, correspondence, and some more. To do what they
need to do, computers require many transistors, but binary numbers made it simpler and less costly.
It requires the least amount of circuitry, which means it takes up the least amount of space,
consumes the least amount of energy, and costs the least amount of money. It also ensures security
and dependability. Having a look and working on this task our comprehension of the binary number
framework has expanded and we got comfortable with the calculation and stream diagram. With
this task research, we came to find out about the historical backdrop of the binary number.
Contribution of Group Member
<NAME OF MEMBER> - He is honest to his work. Working with him gives me the immense pleasure
as he is hard-working and more prone to find the solution to the problem. It is easy to communicate
with him when needed during the application report development.
<NAME OF MEMBER> - The explanation done to the introduction and theoretical part of this
assignment is justified by <NAME>. He is honest and hard-working member of the group with
appropriate knowledge while developing the application of binary number system.
References
Brown, B. (2000). Binary Arithmetic.
Computer Science Department Southern Polytechnic State
University.
Grossman, P. (2008).
Discrete mathematics for computing. . Macmillan International Higher
Education.
Harris, P. (2018).
What are binary and hexadecimal numbers? . New York: PowerKids Press.
Roberts, E. (2016).
Binary Arithmetic and Digital Logic. . Retrieved from web.stanford.edu
Page 10 of 10