Investigation to understand DC circuits

Assignment is done. I need help with paraphrasing. Plagiarism 15%

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
As the capacitor get charged to the battery voltage, charging current goes to zero asymptotically.
Energy is stored in the electric field in the middle of the capacitor sheath by charging the
capacitor. The charging speed is normally defined in form of a time constant RC. The time
constant is the parameter featuring the reaction to a phase input of a first-order. Usually, the
Greek letter τ (tau) is used to denote time constant. The key distinctive unit of a linear time-
invariant (first order LTI) is the time constant.
Time Constant:
All electronic or electrical systems undergo from certain form of “time-delay” amid its output
and input, where a voltage or signal, either alternating, (AC) or continuous (DC) is initially
applied to it. The above delay it is the circuit reaction when a step signal or voltage is applied to
its first. The delay is thus typically well known as time constant or time delay.
The electronic system or the circuit resultant time constant will primarily rely on the reactive
elements either inductive or capacitive linked to it and is a gauge of the reactive time which is
measured in Tau – τ
As shown in the table 1, when rising voltage of DC is applied to a discharged capacitor, the
charging current is drawn by the capacitor and “charges up”. One other side, when there is
decrease in voltage, the discharge of capacitor happen in the reverse direction as shown in table 2
below. The capacitor can act like trivial batteries because of their capacity to store electrical
energy and can discharge or store the power as needed.

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
The capacitor plates charge can be given by formula Q=CV. The above release (discharge) and
storage (charge) of capacitor power is never swift. However, it takes a specific period to happen.
If RC circuit is formed when capacitor is linked in series with resistor, the capacitor will charge
progressively through the resistor up to when the capacitor voltage levels with the supply
voltage. The transient response which is time needed for capacitor to completely charge is equal
to approximately 5-time constants (5T).
τ = R x C, in seconds is used to measure the transient response, where the letter C denotes the
capacitor value in Farads and R is the resistor value in ohms. The above creates the foundations
of an RC charging circuit were 5-time constants can be contemplated as “5*RC”.
Charging capacitors:
Time (s) Recorded voltage value (v) Calculate voltage value (v)
0 0 0
10 1.08 1.68
20 2.33 3.05
30 3.39 4.16
40 4.30 5.06
50 5.02 5.80
60 5.65 6.40
70 6.17 6.88
80 6.57 7.28
90 6.85 7.60
100 7.06 7.86
110 7.17 8.07

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
120 7.23 8.25
130 7.26 8.39
140 7.28 8.50
150 7.28 8.60
Capacitor= 0.0022F
Resistor = 22000Ω
Voltage = 9V
CR = 48.4
Vc= V0 (1-e-t/RC)
Vc= 9(1-e-50/48.4)
Vc= 5.80 volts
After 50s, calculate voltage is 5.80 volts which is closer to recorded voltage 5.02 volts.
A voltage-time graphs for a charging recorded capacitor and calculated capacitor.
1 time constant
V= Vo (1-e-1)
V= 9(1-e-1)
V= 5.69 volts
Percentage = (5.69/9) x 100
= 63.2 %

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
My recorded value for 60% is 5.65 volts. It is closer to 1-time constant.
3 time constant
V= 9(1-e-3)
V = 8.55 volts
% = (8.55/9) x 100
=95.02%
5 time constant
V= 9(1-e-5)
=8.94 volts
% = (8.94/9) x 100
= 99.32%
It is worth noting that capacitor can never be 100% completely charged because of the stored
energy in the capacitor. Therefore, capacitor is fully charged after 5T. The RC circuit charging
curve is exponential.

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
Capacitor Discharging Graph
Also, when the switch is closed and the battery removed and substituted by a short circuit,
through the resistor, the capacitor would discharge itself back. The power stored in the capacitor
is removed as the capacitor discharges its current over the resistor series. Then. The voltage in
the capacitor decays to 0.
The circuit resistance product or the circuit capacitance is equivalent to the RC time constant.
T = RC
It is the period needed to charge capacity, equal to 63.2% of the different between the final and
initial value and the capacitor discharge equivalence of 36.8%. The value is derivative of
exponential e which is a mathematical constant, particularly 1 - e -1, which is the capacitor
voltage to charge against the time required.
Time (s) Recorded voltage (v) Calculate voltage (v)
0 7.25 9
10 5.93 7.32
20 5.05 5.95
30 4.32 4.84
40 3.71 3.94
50 3.20 3.20
60 2.80 2.61
70 2.43 2.12
80 2.11 1.72
90 1.84 1.40
100 1.62 1.14

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
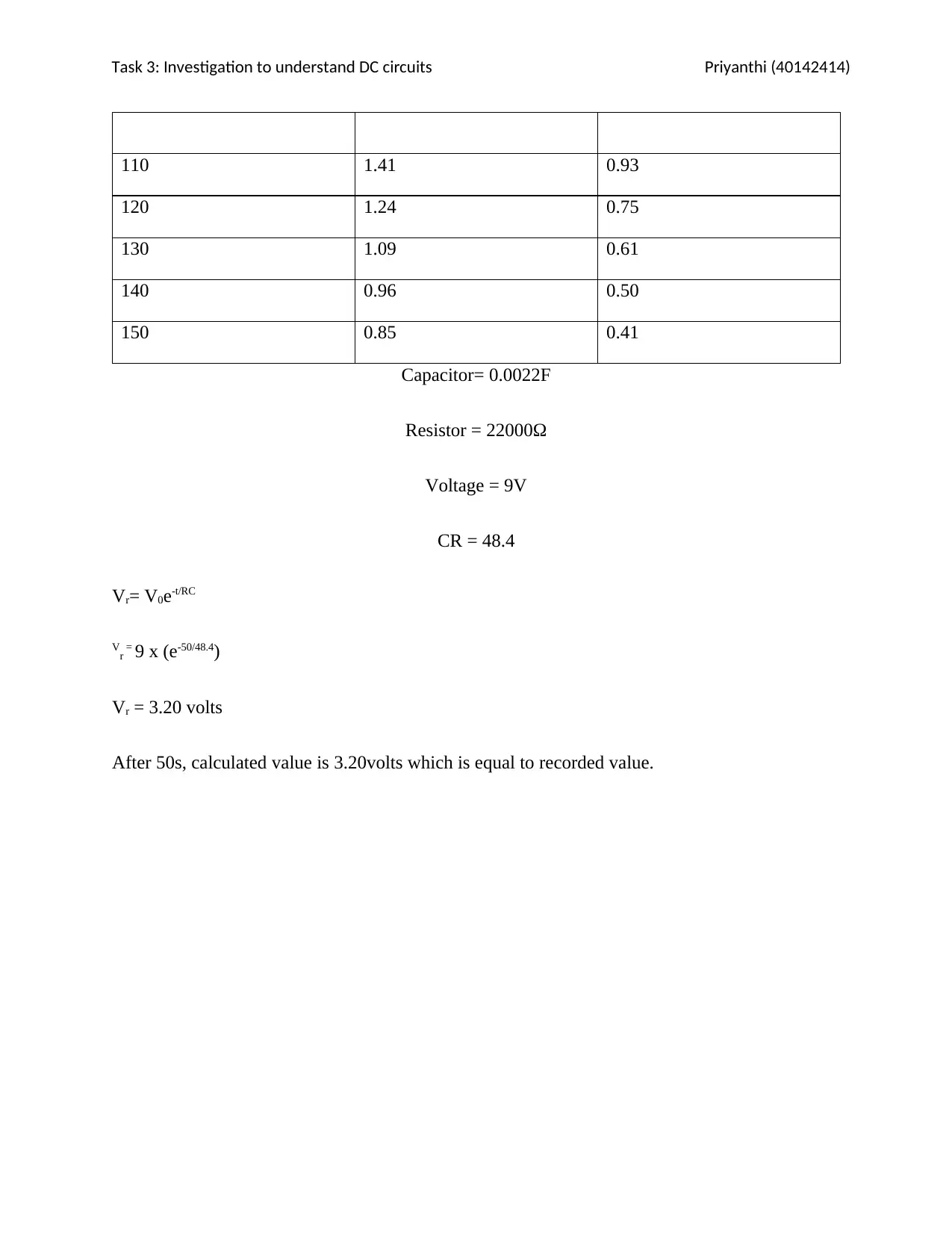
110 1.41 0.93
120 1.24 0.75
130 1.09 0.61
140 0.96 0.50
150 0.85 0.41
Capacitor= 0.0022F
Resistor = 22000Ω
Voltage = 9V
CR = 48.4
Vr= V0e-t/RC
Vr = 9 x (e-50/48.4)
Vr = 3.20 volts
After 50s, calculated value is 3.20volts which is equal to recorded value.

Task 3: Investigation to understand DC circuits Priyanthi (40142414)
References
IamTechnical.com. 2019. Capacitor Charging Graph | IamTechnical.com. [ONLINE] Available
at: http://iamtechnical.com/capacitor-charging-graph. [Accessed 16 December 2019].