Association between Alcohol Consumption and Alcohol-related Events

This article examines the association between level of alcohol consumption and alcohol-related events in a cohort study. It calculates the rate ratio and stratum-specific measures of effect to determine the relationship between alcohol consumption and the occurrence of alcohol-related events. The study analyzes data from different socioeconomic statuses to provide a comprehensive understanding of the impact of alcohol consumption on health outcomes.

UNIVERSITY OF TECHNOLOGY SYDNEY
92296 EPIDEMIOLOGY AND POPULATION HEALTH AUTUMN 2019
ASSESSMENT 2

Question 1 [17 marks]
Cancer is a leading cause of death worldwide. In this question, you will examine deaths from
cancer in Australia and Argentina in 2013. The cancer deaths for both countries exclude non-
melanoma skin cancers.
1. Tables 1 and 2 give the number of deaths due to cancer in Australia in 2013 and
Argentina in 2013, respectively, and the estimated population by age group for each
year. Use this information to answer the following questions.
Table 1: Crude and age-specific death rates due to cancer, Australia, 2013
Age group
(years)
Deaths Total
Population
Death rate per
100,000 population
0-14 98 4,482,710 2.186
15-39 633 8,234,440 7.69
40-44 524 1,655,519 31.65
45-49 982 1,559,507 62.97
50-54 1,776 1,569,432 113.16
55-59 2,635 1,451,868 181.49
60-64 3,863 1,281,614 301.42
65-69 5,287 1,153,780 458.2
70-74 5,633 843,696 667.5
75+ 22,081 1,566,990 1409.4
TOTAL (all ages)* 43,512 23,799,556 182.8
Table 2: Crude and age-specific death rates due to cancer, Argentina 2013
Age group
(years)
Deaths Total
Population
Death rate per
100,000 population
0-14 388 10,939,513 3.55
15-39 2,333 16,642,359 7.769
40-44 1,293 2,693,223 74
45-49 1,993 2,359,742 84.46
50-54 3,379 2,192,512 154.11
55-59 5,101 2,031,042 251.15
60-64 6,874 1,815,418 378.65

65-69 7,965 1,513,164 526.38
70-74 8,124 1,173,119 692.5
75+ 22,546 2,057,673 1095.7
TOTAL (all ages)* 59,996 43,473,765 138
a) Calculate the crude death rates for Australia and Argentina. Interpret the rates. [2
marks]
From the tables:
Crude death rate for Australia=43512/23799556*100000
=183.16 @ 100000 persons per year
Crude death rate for Argentina=59996/43473765*100000
=138 @ 100000 persons per year
Crude death rate for Australia for Argentina is lower than that of Australia
Calculate the age-specific death rates to complete Tables 1 and 2. Give an example of your
working. [2 marks]
Age-specific death rates (0-14) age group in Argentina=388/10993513*100000=3.5 @
100000 people-years
b) Graph the age-specific death rates for Australia and Argentina using an appropriate
graph. Comment on the graph. [2 marks]

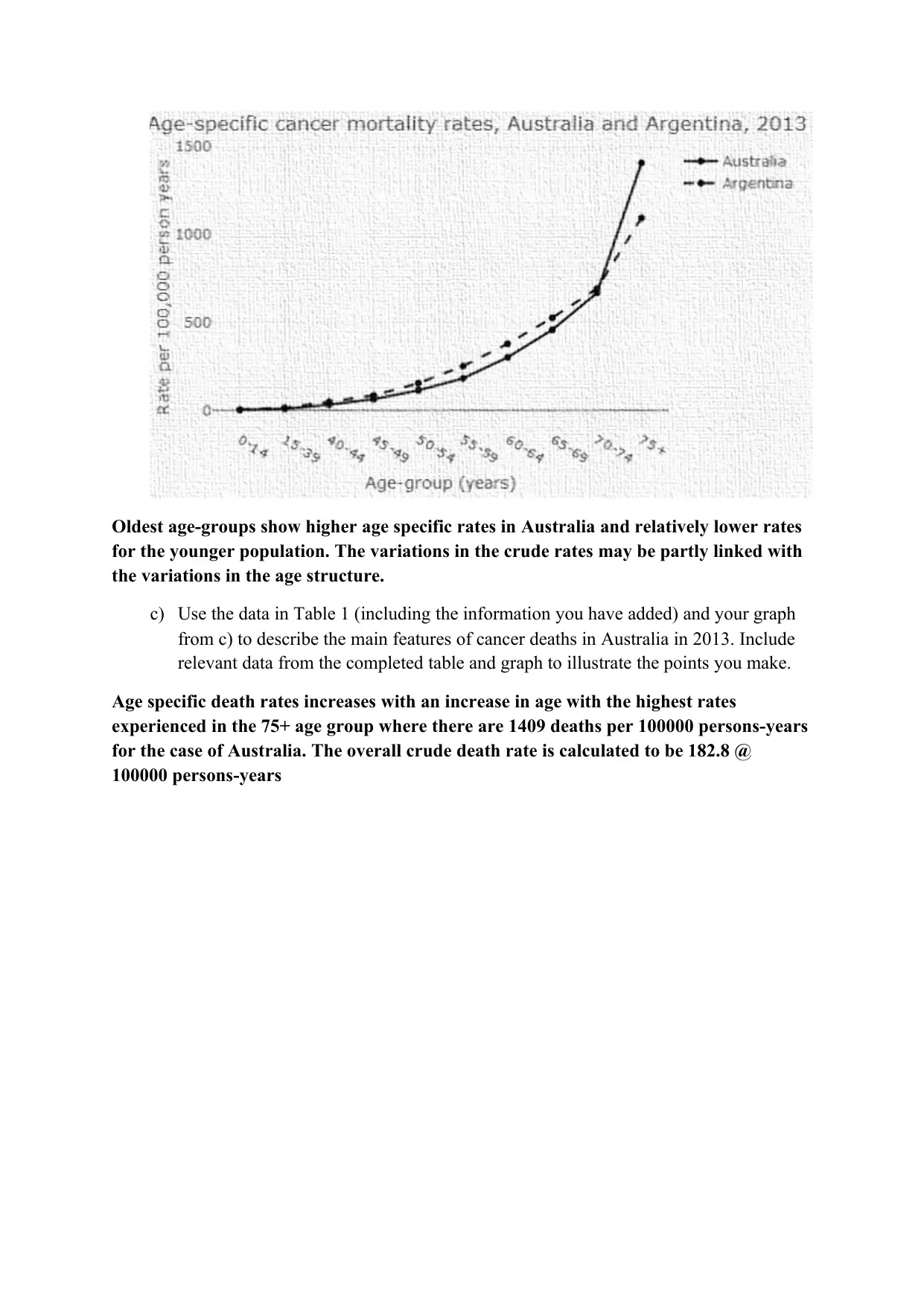
Oldest age-groups show higher age specific rates in Australia and relatively lower rates
for the younger population. The variations in the crude rates may be partly linked with
the variations in the age structure.
c) Use the data in Table 1 (including the information you have added) and your graph
from c) to describe the main features of cancer deaths in Australia in 2013. Include
relevant data from the completed table and graph to illustrate the points you make.
Age specific death rates increases with an increase in age with the highest rates
experienced in the 75+ age group where there are 1409 deaths per 100000 persons-years
for the case of Australia. The overall crude death rate is calculated to be 182.8 @
100000 persons-years

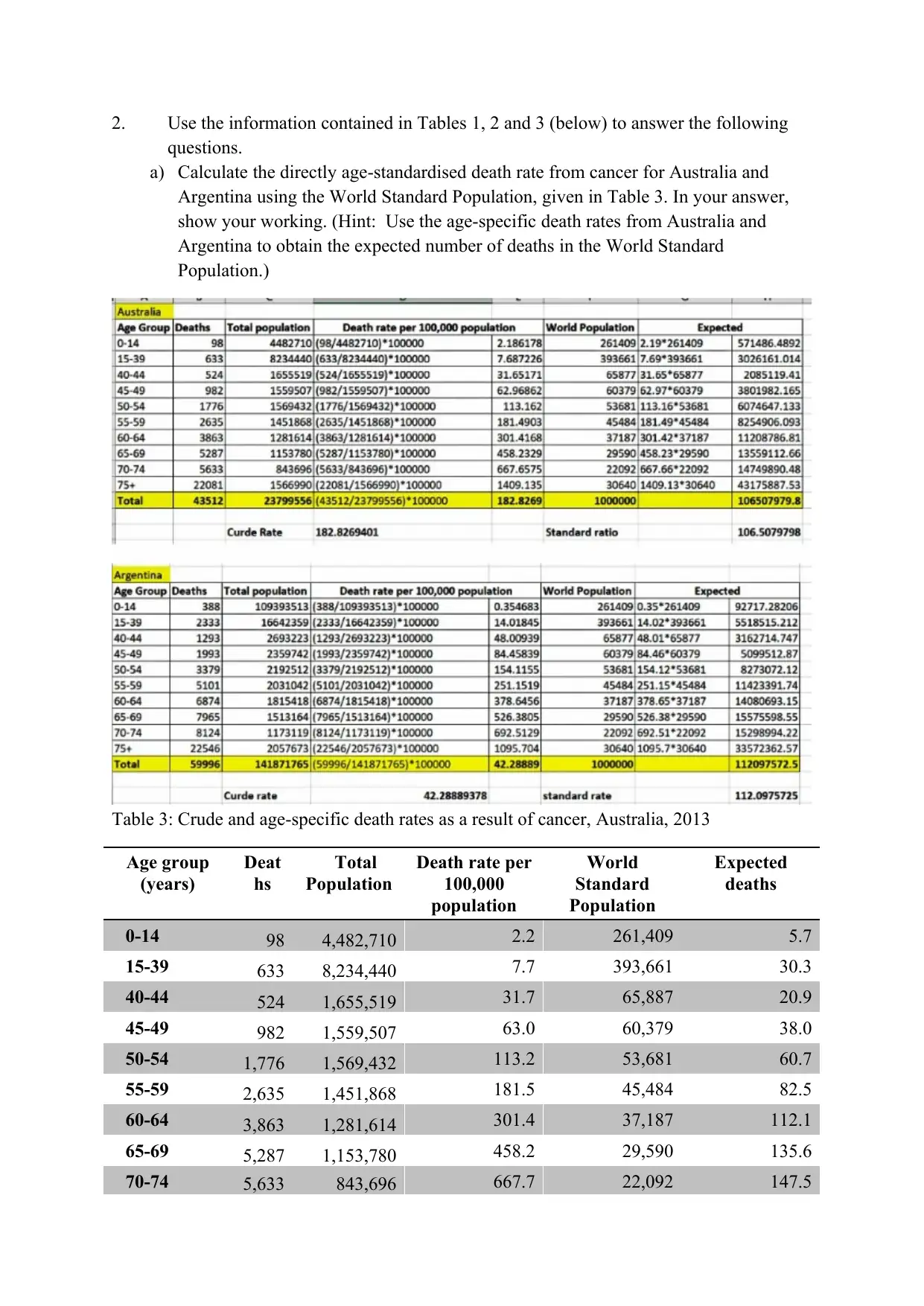
2. Use the information contained in Tables 1, 2 and 3 (below) to answer the following
questions.
a) Calculate the directly age-standardised death rate from cancer for Australia and
Argentina using the World Standard Population, given in Table 3. In your answer,
show your working. (Hint: Use the age-specific death rates from Australia and
Argentina to obtain the expected number of deaths in the World Standard
Population.)
Table 3: Crude and age-specific death rates as a result of cancer, Australia, 2013
Age group
(years)
Deat
hs
Total
Population
Death rate per
100,000
population
World
Standard
Population
Expected
deaths
0-14 98 4,482,710 2.2 261,409 5.7
15-39 633 8,234,440 7.7 393,661 30.3
40-44 524 1,655,519 31.7 65,887 20.9
45-49 982 1,559,507 63.0 60,379 38.0
50-54 1,776 1,569,432 113.2 53,681 60.7
55-59 2,635 1,451,868 181.5 45,484 82.5
60-64 3,863 1,281,614 301.4 37,187 112.1
65-69 5,287 1,153,780 458.2 29,590 135.6
70-74 5,633 843,696 667.7 22,092 147.5

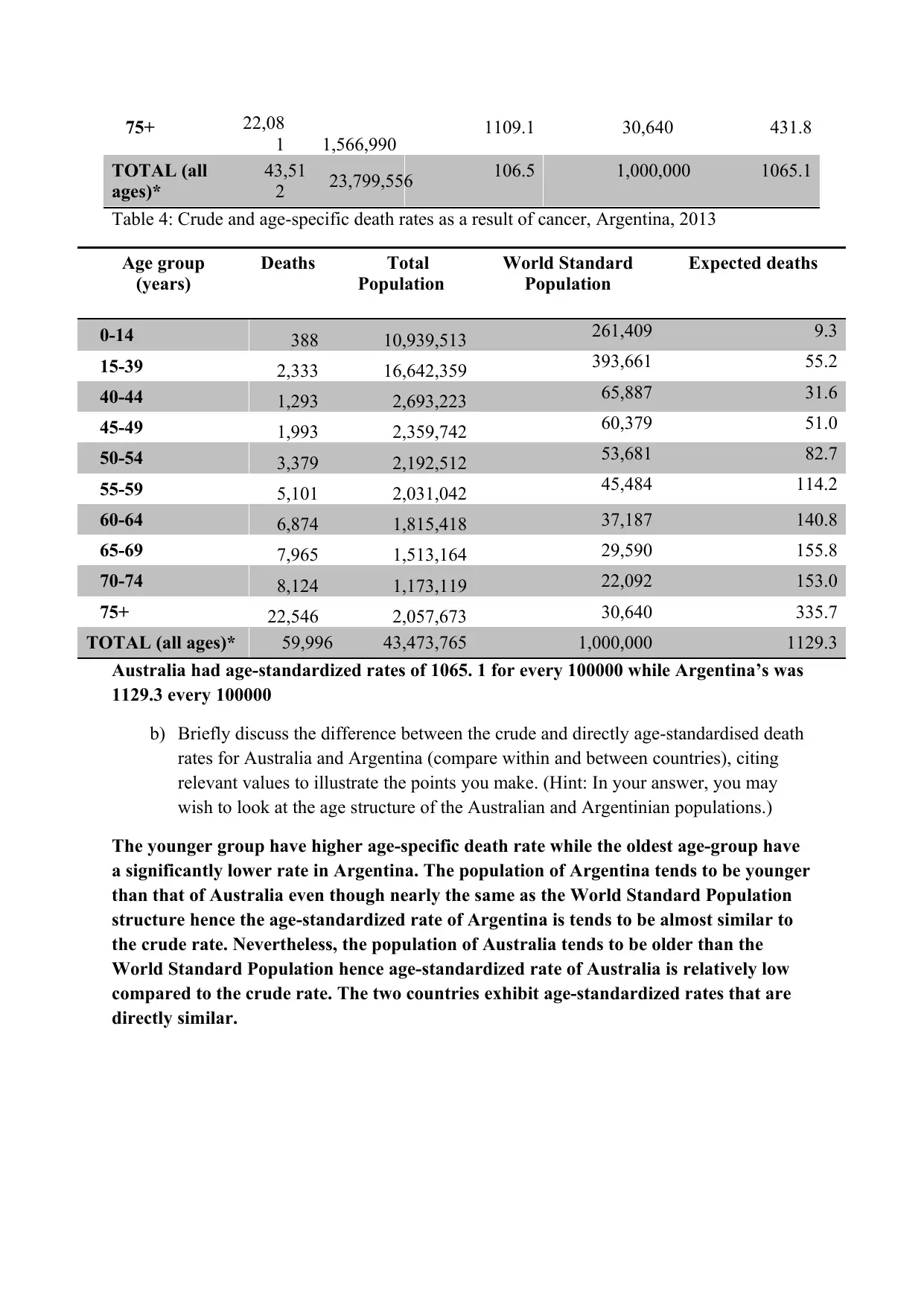
75+ 22,08
1 1,566,990 1109.1 30,640 431.8
TOTAL (all
ages)*
43,51
2 23,799,556 106.5 1,000,000 1065.1
Table 4: Crude and age-specific death rates as a result of cancer, Argentina, 2013
Age group
(years)
Deaths Total
Population
World Standard
Population
Expected deaths
0-14 388 10,939,513 261,409 9.3
15-39 2,333 16,642,359 393,661 55.2
40-44 1,293 2,693,223 65,887 31.6
45-49 1,993 2,359,742 60,379 51.0
50-54 3,379 2,192,512 53,681 82.7
55-59 5,101 2,031,042 45,484 114.2
60-64 6,874 1,815,418 37,187 140.8
65-69 7,965 1,513,164 29,590 155.8
70-74 8,124 1,173,119 22,092 153.0
75+ 22,546 2,057,673 30,640 335.7
TOTAL (all ages)* 59,996 43,473,765 1,000,000 1129.3
Australia had age-standardized rates of 1065. 1 for every 100000 while Argentina’s was
1129.3 every 100000
b) Briefly discuss the difference between the crude and directly age-standardised death
rates for Australia and Argentina (compare within and between countries), citing
relevant values to illustrate the points you make. (Hint: In your answer, you may
wish to look at the age structure of the Australian and Argentinian populations.)
The younger group have higher age-specific death rate while the oldest age-group have
a significantly lower rate in Argentina. The population of Argentina tends to be younger
than that of Australia even though nearly the same as the World Standard Population
structure hence the age-standardized rate of Argentina is tends to be almost similar to
the crude rate. Nevertheless, the population of Australia tends to be older than the
World Standard Population hence age-standardized rate of Australia is relatively low
compared to the crude rate. The two countries exhibit age-standardized rates that are
directly similar.

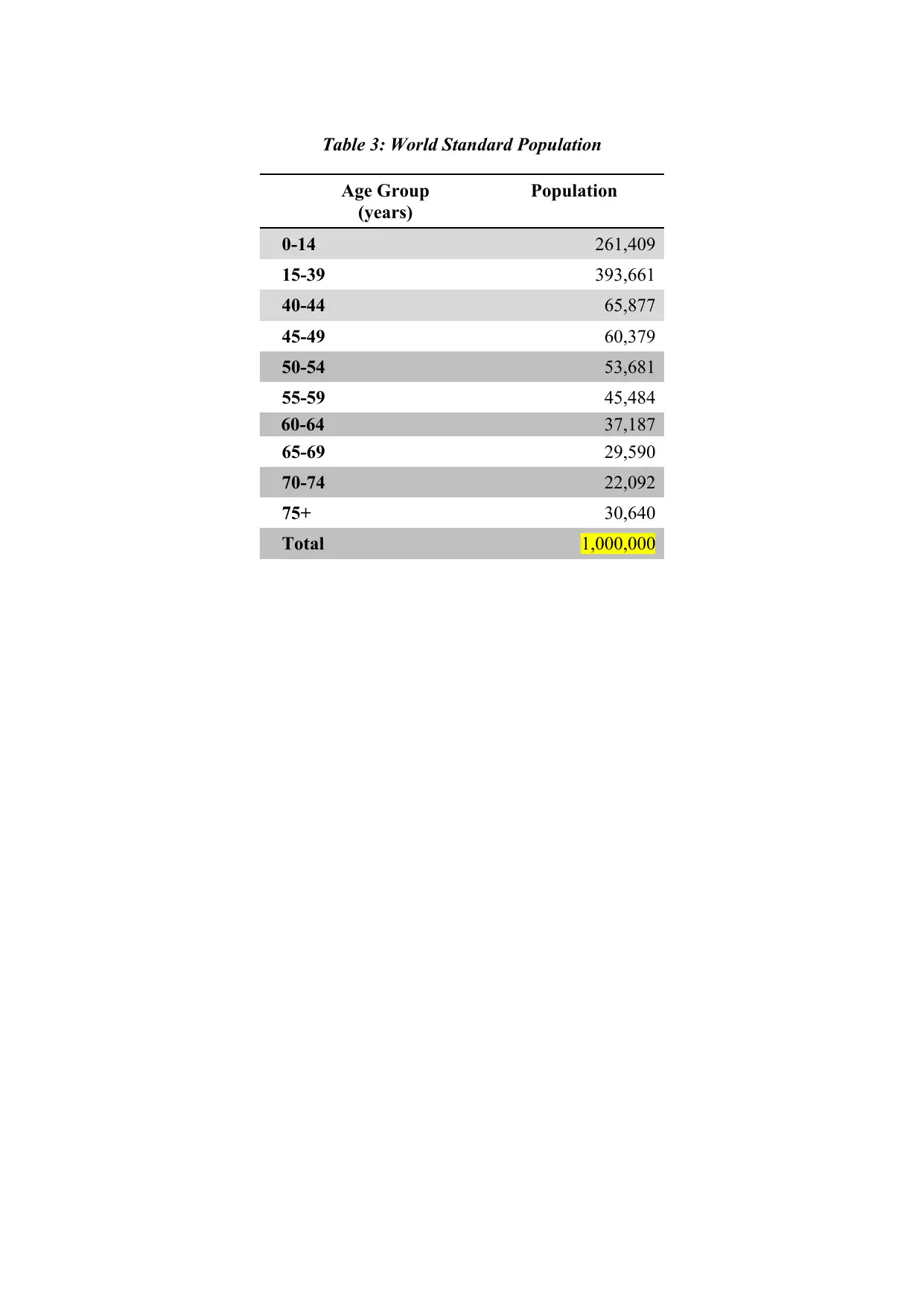
Table 3: World Standard Population
Age Group
(years)
Population
0-14 261,409
15-39 393,661
40-44 65,877
45-49 60,379
50-54 53,681
55-59 45,484
60-64 37,187
65-69 29,590
70-74 22,092
75+ 30,640
Total 1,000,000

Question 2 [13 marks]
A cohort study looked at the association between HIV status and all-cause mortality among
prisoners. There were 850 prisoners who were HIV positive and 21 500 who were HIV
negative in the study. The data from the study are reported in Table 4 below. In this question,
provide all working for your calculations.
Table 4: Deaths from all causes by HIV status in prisoners
Deaths Person-years of follow-up
HIV positive 325 8 820
HIV negative 2 460 265 000
Total 2 785 273 820
1. Calculate the rate ratio for all-cause mortality to compare mortality by HIV status. [2
marks]
Incidence rate in HIV positive people=325/8820=0.0368
Incidence rate in HIV negative people=2460/26500=0.0928
Rate ratio=ratio of the above calculations=0.0928/0.0368=3.97
Interpretation: Likelihood of people with HIV dying is 4 times more than HIV negative
people
2. What was the (absolute) difference in mortality rates by HIV status? Interpret your
answer.
Absolute difference=325/8820-2460/26500
=27.57 every 1000 person-years hence there are 27.6 more deaths per 1000 person-years
in for HIV positive people in comparison with HIV negative individuals
3. Now calculate the proportion of deaths prisoners that would have not occurred in the
absence of HIV (the attributable fraction). Give an interpretation of your answer.
Attributable fraction= (325/8820-2460/26500)/325/8820

=0.748. This means 74.8% of the mortality cases among HIV positive individuals are
directly linked to HIV.
4. What is the overall incidence of mortality?
Overall incidence of mortality =2785/273820
=10.17 for every 1000 person-years
5. What would the incidence of mortality be if there was no HIV?
Incidence of mortality (No HIV) =2460/26500=9.8 for every 1000 person-years
6. Using 4 and 5, calculate the population attributable risk. Interpret the population
attributable risk.
Population attributable risk=2785/273820-2460/26500
=0.89 for every 1000 person-years.
Interpretation: 0.89 deaths can be prevented, in the absence of HIV, of the entire
population
7. Now calculate and interpret the population attributable fraction. [2 marks]
Attributable fraction= (2785/27820-2460/26500)/2785/278320
=0.087
Interpretation: 8.7% of the deaths can be evaded in case there is no HIV in the cohort
study

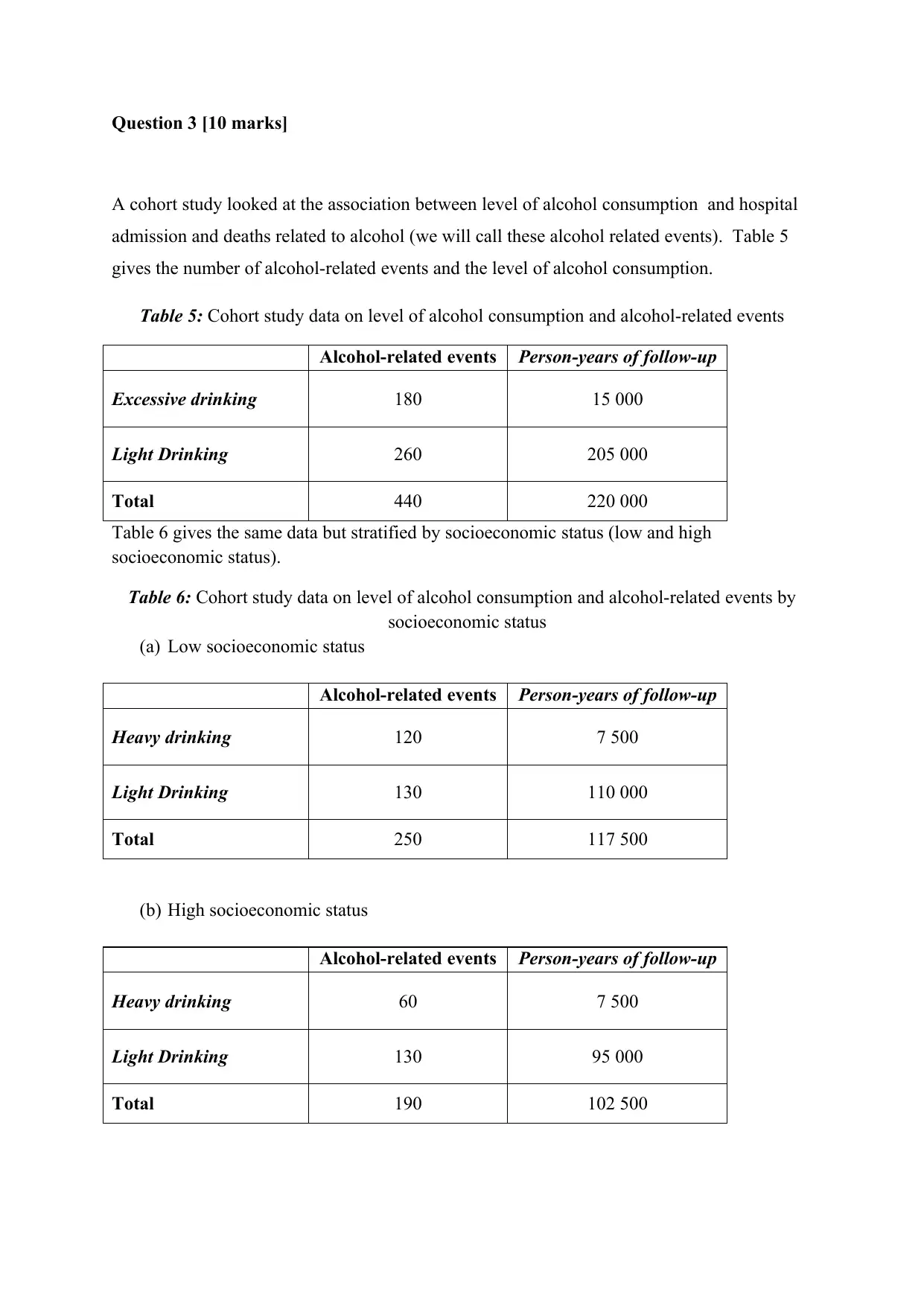
Question 3 [10 marks]
A cohort study looked at the association between level of alcohol consumption and hospital
admission and deaths related to alcohol (we will call these alcohol related events). Table 5
gives the number of alcohol-related events and the level of alcohol consumption.
Table 5: Cohort study data on level of alcohol consumption and alcohol-related events
Alcohol-related events Person-years of follow-up
Excessive drinking 180 15 000
Light Drinking 260 205 000
Total 440 220 000
Table 6 gives the same data but stratified by socioeconomic status (low and high
socioeconomic status).
Table 6: Cohort study data on level of alcohol consumption and alcohol-related events by
socioeconomic status
(a) Low socioeconomic status
Alcohol-related events Person-years of follow-up
Heavy drinking 120 7 500
Light Drinking 130 110 000
Total 250 117 500
(b) High socioeconomic status
Alcohol-related events Person-years of follow-up
Heavy drinking 60 7 500
Light Drinking 130 95 000
Total 190 102 500

1. Calculate the appropriate measure of effect for the association between level of alcohol
consumption and alcohol-related events.
The rate ratio is the appropriate measure of the effect for this problem
Rate Ratio= (180/15000)/ (260/20500) =9.46
2. Calculate the stratum-specific appropriate measures of effect.
Stratum-specific appropriate measures of effect are calculated as:
Rate Ratio= (120/7500)/ (130/110000) =13.54; this is the value for the low socio-
economic status
Rate Ratio= (60/7500)/ (130/95000) =5.84; this is the value for the high socio-economic
status
3. Using 1 and 2 above, discuss whether socioeconomic status is a confounder or an effect
modifier.
The stratum-specific rate ratios as can be seen from the preceding calculations vary
significantly from the crude rate ratio. This is a suggestion of the presence of effect
modification hence the socioeconomic status is an effect modifier. Effect modification
revolves around stratification and takes place in case an exposure has a different impact
among various subgroups. Effect modifiers are correlated with the outcome as opposed
to the exposure. In the context of epidemiology, effect modification has a relationship
with the biology of the disease as opposed to data observation. As can be noted in the
above data, alcohol consumption has a direct proportionality with the number of person
follow ups.

References
Benchimol, E.I., Bernstein, C.N., Bitton, A., Carroll, M.W., Singh, H., Otley, A.R.,
Vutcovici, M., El-Matary, W., Nguyen, G.C., Griffiths, A.M. and Mack, D.R., 2017. Trends
in epidemiology of pediatric inflammatory bowel disease in Canada: distributed network
analysis of multiple population-based provincial health administrative databases. The
American journal of gastroenterology, 112(7), p.1120
Mooney, S.J., Westreich, D.J. and El-Sayed, A.M., 2015. Epidemiology in the era of big
data. Epidemiology (Cambridge, Mass.), 26(3), p.390
Ornstein, K.A., Leff, B., Covinsky, K.E., Ritchie, C.S., Federman, A.D., Roberts, L., Kelley,
A.S., Siu, A.L. and Szanton, S.L., 2015. Epidemiology of the homebound population in the
United States. JAMA internal medicine, 175(7), pp.1180-1186
Khoury, M.J. and Ioannidis, J.P., 2014. Big data meets public health. Science, 346(6213),
pp.1054-1055