Impact of Covariates on Time to Develop Coronary Heart Disease
VerifiedAdded on 2019/12/28
|32
|4225
|238
Report
AI Summary
This assignment content aims to identify the factors that determine the time to develop coronary heart disease using a Cox proportional hazards model. The analysis reveals that age is the statistically significant predictor of time to develop coronary heart disease, with each year increase in age increasing the risk of dying by 1048 times. The results also indicate that BMI, SBP, and cholesterol levels are associated with an increased probability of suffering from CHD. The significance of the Cox proportional hazards model over logistic regression is discussed, highlighting its flexibility in identifying the probability of certain events occurring in different situations.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

STATISTICS
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
TABLE OF CONTENTS
INTRODUCTION.......................................................................................................................................................................................3
Question 1....................................................................................................................................................................................................3
a. Determine whether there is a significant association between systolic blood pressure and gender....................................................3
b. Determine whether there is a significant association between systolic blood pressure and BMI category. Interpret your results.....5
c. Determine whether there is a significant association between systolic blood pressure and age as well as cholesterol......................6
Question 2..................................................................................................................................................................................................13
(a) Logistic regression...........................................................................................................................................................................13
Question 3..................................................................................................................................................................................................16
A. Carry out a Kaplan-Meier survival analysis.....................................................................................................................................16
(b) Construct a survival plot and conduct a hypothesis test using the log rank test..............................................................................17
© Cox regression...................................................................................................................................................................................20
...................................................................................................................................................................................................................23
(d) Significance of Cox proportional hazards model rather that logistic regression to determine which factors are associated with
coronary heart disease............................................................................................................................................................................24
CONCLUSION..........................................................................................................................................................................................24
INTRODUCTION.......................................................................................................................................................................................3
Question 1....................................................................................................................................................................................................3
a. Determine whether there is a significant association between systolic blood pressure and gender....................................................3
b. Determine whether there is a significant association between systolic blood pressure and BMI category. Interpret your results.....5
c. Determine whether there is a significant association between systolic blood pressure and age as well as cholesterol......................6
Question 2..................................................................................................................................................................................................13
(a) Logistic regression...........................................................................................................................................................................13
Question 3..................................................................................................................................................................................................16
A. Carry out a Kaplan-Meier survival analysis.....................................................................................................................................16
(b) Construct a survival plot and conduct a hypothesis test using the log rank test..............................................................................17
© Cox regression...................................................................................................................................................................................20
...................................................................................................................................................................................................................23
(d) Significance of Cox proportional hazards model rather that logistic regression to determine which factors are associated with
coronary heart disease............................................................................................................................................................................24
CONCLUSION..........................................................................................................................................................................................24
INTRODUCTION
Heart related diseases are increasing across the globe and number of people affected from same are increasing consistently. In
the current report varied data analysis tools are applied on the given data set. In this regard regression and other models are applied on
the data set and answers are interpreted in systematic way. Useful meanings are deduced from the regression results and same of other
methods. In this way entire research work is carried out in the report.
Question 1
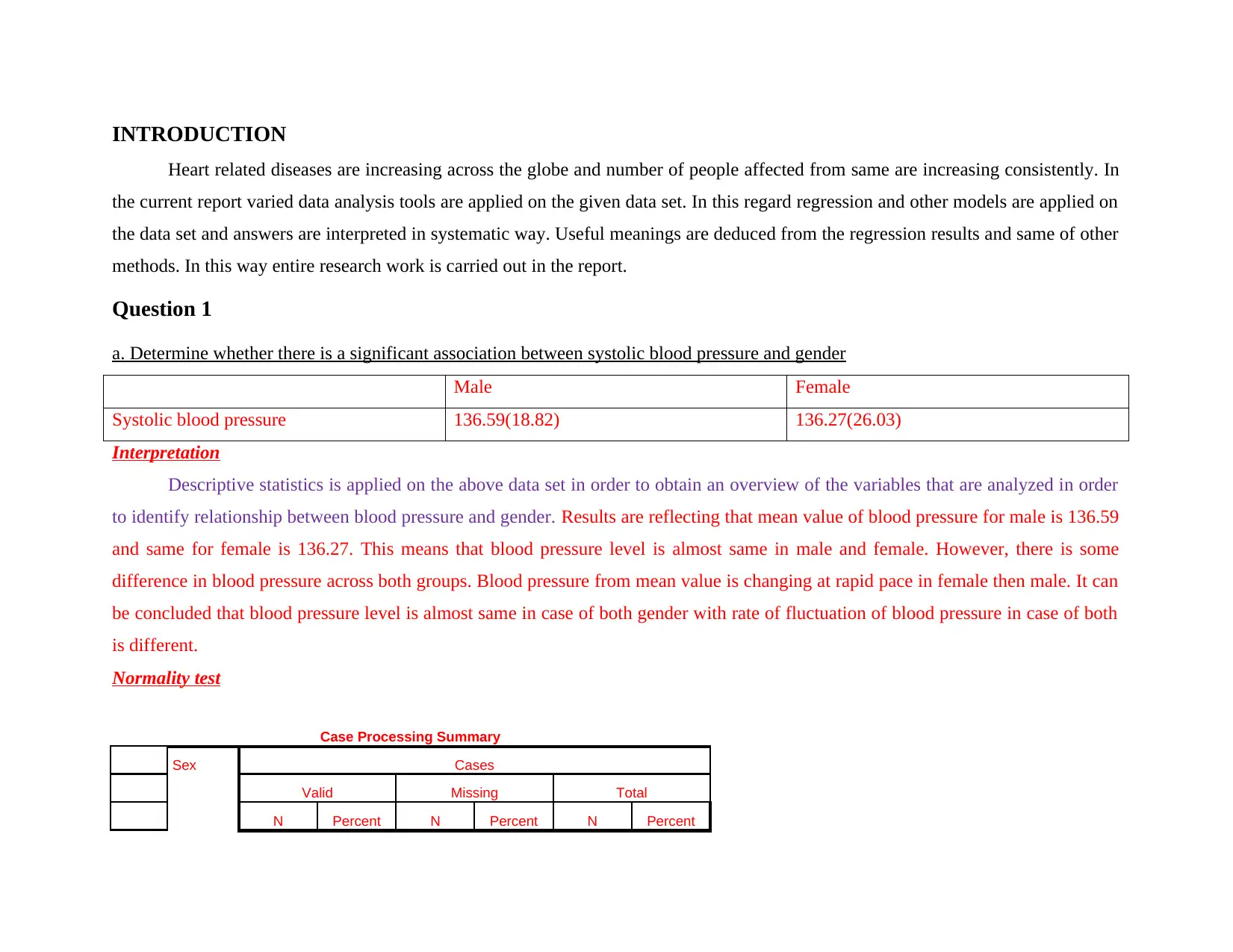
a. Determine whether there is a significant association between systolic blood pressure and gender
Male Female
Systolic blood pressure 136.59(18.82) 136.27(26.03)
Interpretation
Descriptive statistics is applied on the above data set in order to obtain an overview of the variables that are analyzed in order
to identify relationship between blood pressure and gender. Results are reflecting that mean value of blood pressure for male is 136.59
and same for female is 136.27. This means that blood pressure level is almost same in male and female. However, there is some
difference in blood pressure across both groups. Blood pressure from mean value is changing at rapid pace in female then male. It can
be concluded that blood pressure level is almost same in case of both gender with rate of fluctuation of blood pressure in case of both
is different.
Normality test
Case Processing Summary
Sex Cases
Valid Missing Total
N Percent N Percent N Percent
Heart related diseases are increasing across the globe and number of people affected from same are increasing consistently. In
the current report varied data analysis tools are applied on the given data set. In this regard regression and other models are applied on
the data set and answers are interpreted in systematic way. Useful meanings are deduced from the regression results and same of other
methods. In this way entire research work is carried out in the report.
Question 1
a. Determine whether there is a significant association between systolic blood pressure and gender
Male Female
Systolic blood pressure 136.59(18.82) 136.27(26.03)
Interpretation
Descriptive statistics is applied on the above data set in order to obtain an overview of the variables that are analyzed in order
to identify relationship between blood pressure and gender. Results are reflecting that mean value of blood pressure for male is 136.59
and same for female is 136.27. This means that blood pressure level is almost same in male and female. However, there is some
difference in blood pressure across both groups. Blood pressure from mean value is changing at rapid pace in female then male. It can
be concluded that blood pressure level is almost same in case of both gender with rate of fluctuation of blood pressure in case of both
is different.
Normality test
Case Processing Summary
Sex Cases
Valid Missing Total
N Percent N Percent N Percent
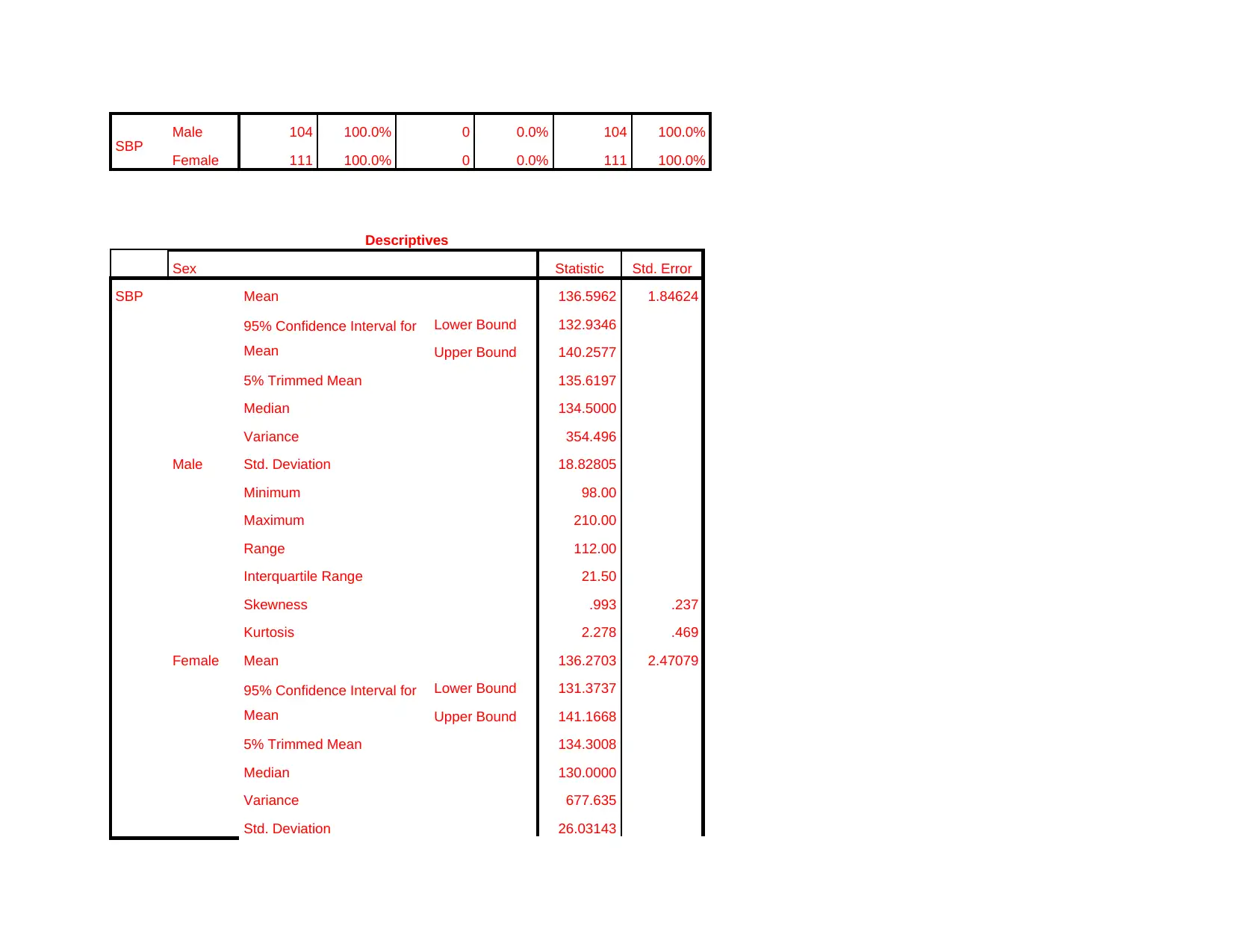
SBP Male 104 100.0% 0 0.0% 104 100.0%
Female 111 100.0% 0 0.0% 111 100.0%
Descriptives
Sex Statistic Std. Error
SBP
Male
Mean 136.5962 1.84624
95% Confidence Interval for
Mean
Lower Bound 132.9346
Upper Bound 140.2577
5% Trimmed Mean 135.6197
Median 134.5000
Variance 354.496
Std. Deviation 18.82805
Minimum 98.00
Maximum 210.00
Range 112.00
Interquartile Range 21.50
Skewness .993 .237
Kurtosis 2.278 .469
Female Mean 136.2703 2.47079
95% Confidence Interval for
Mean
Lower Bound 131.3737
Upper Bound 141.1668
5% Trimmed Mean 134.3008
Median 130.0000
Variance 677.635
Std. Deviation 26.03143
Female 111 100.0% 0 0.0% 111 100.0%
Descriptives
Sex Statistic Std. Error
SBP
Male
Mean 136.5962 1.84624
95% Confidence Interval for
Mean
Lower Bound 132.9346
Upper Bound 140.2577
5% Trimmed Mean 135.6197
Median 134.5000
Variance 354.496
Std. Deviation 18.82805
Minimum 98.00
Maximum 210.00
Range 112.00
Interquartile Range 21.50
Skewness .993 .237
Kurtosis 2.278 .469
Female Mean 136.2703 2.47079
95% Confidence Interval for
Mean
Lower Bound 131.3737
Upper Bound 141.1668
5% Trimmed Mean 134.3008
Median 130.0000
Variance 677.635
Std. Deviation 26.03143
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
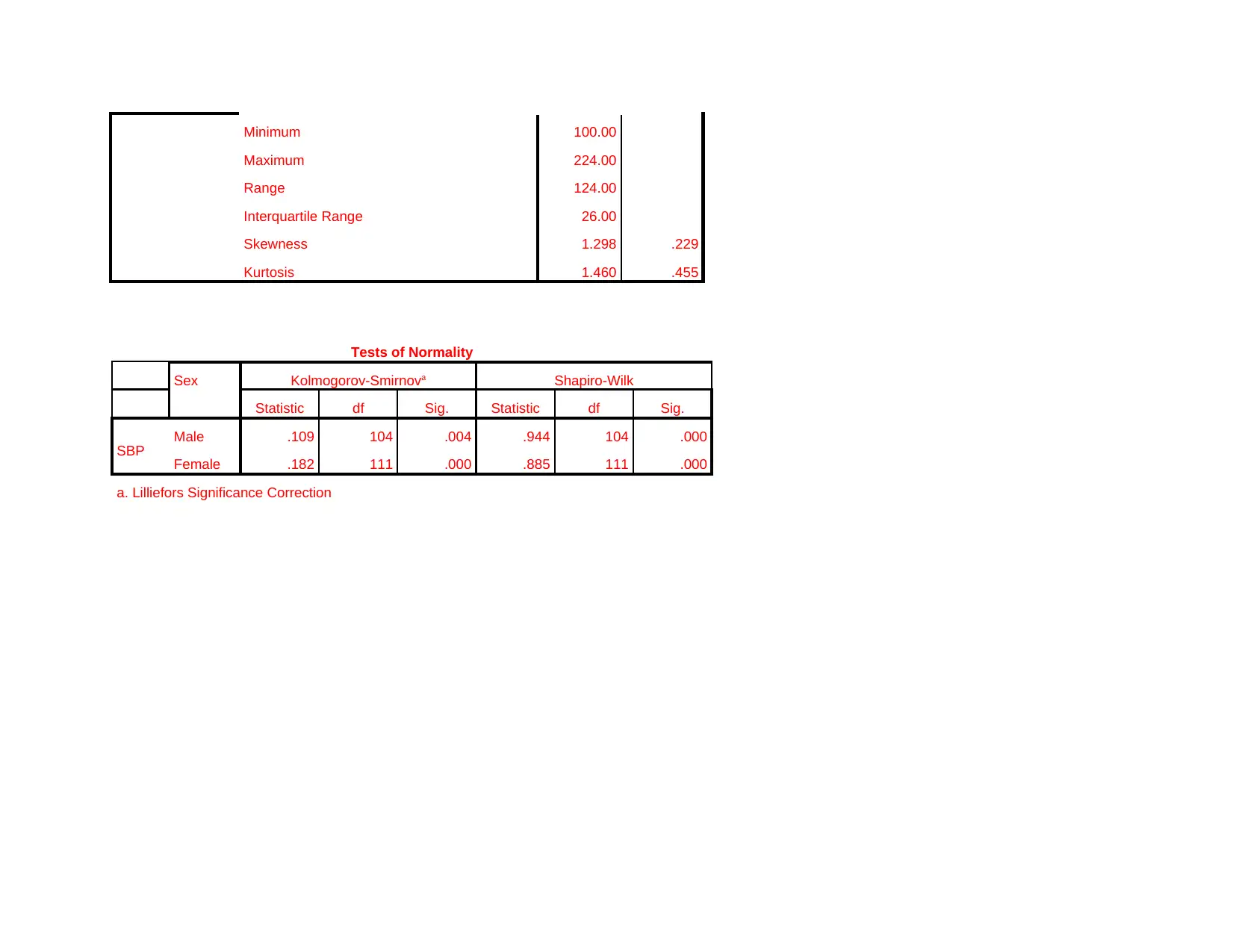
Minimum 100.00
Maximum 224.00
Range 124.00
Interquartile Range 26.00
Skewness 1.298 .229
Kurtosis 1.460 .455
Tests of Normality
Sex Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP Male .109 104 .004 .944 104 .000
Female .182 111 .000 .885 111 .000
a. Lilliefors Significance Correction
Maximum 224.00
Range 124.00
Interquartile Range 26.00
Skewness 1.298 .229
Kurtosis 1.460 .455
Tests of Normality
Sex Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP Male .109 104 .004 .944 104 .000
Female .182 111 .000 .885 111 .000
a. Lilliefors Significance Correction

Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Interpretation
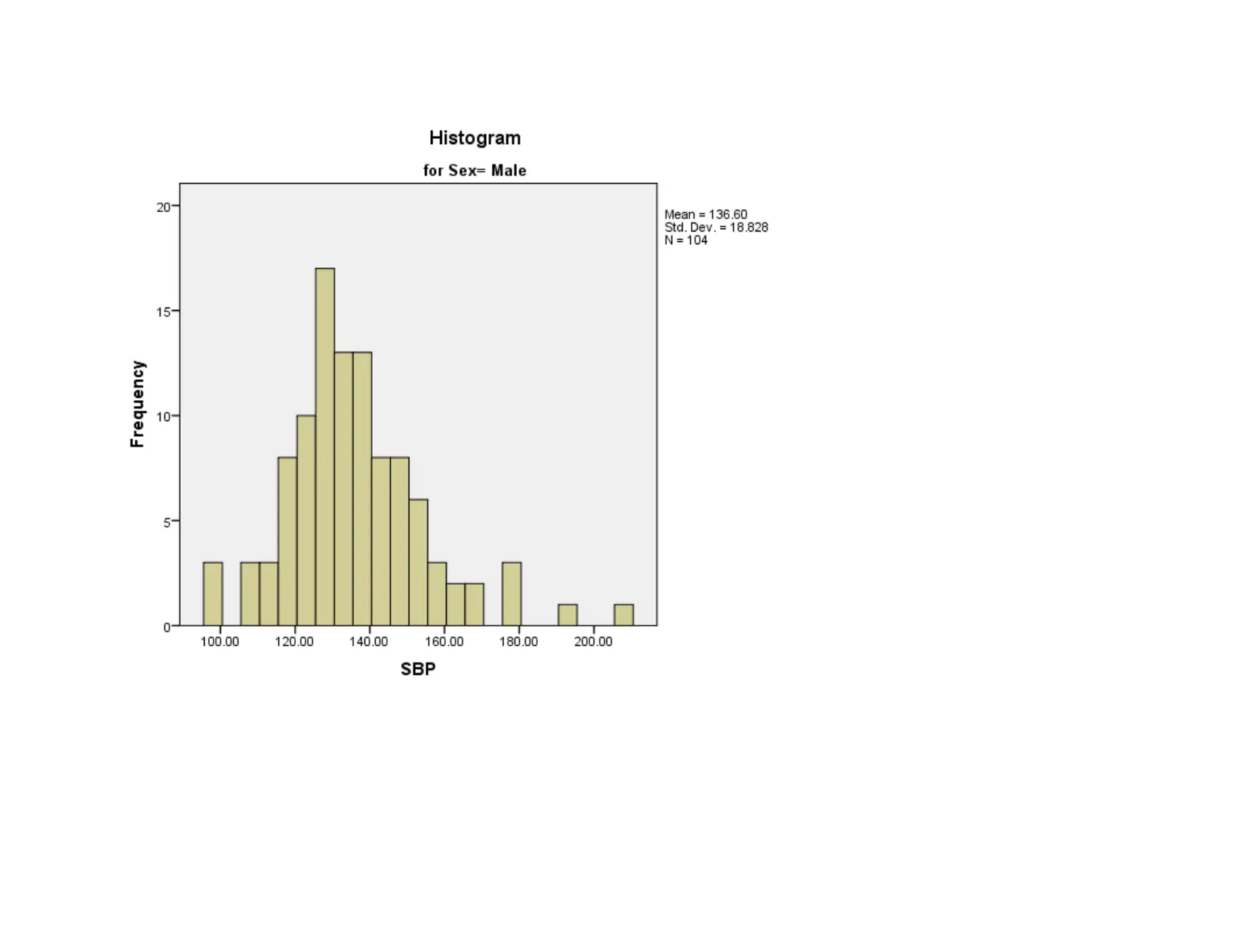
Results are reflecting that data is not normally distributed. Significance value of Shapiro Wilk test is 0.00<0.05 which means
that data is not normally distributed. Histogram chart is prepared as part of normality test and it can be observed that in case of male
there is normality in the data to some extent as curve is bell shaped but not properly shaped. In case of female category histogram is
clearly reflecting that curve is not bell shaped. Thus, it can be said that data is not normally distributed as reflected by Shapiro wilk
test.
H0: There is no significant mean difference between gender and blood pressure.
H1: There is significant mean difference between gender and blood pressure.
Group Statistics
Sex N Mean Std. Deviation Std. Error Mean
SBP Male 104 136.5962 18.82805 1.84624
Female 111 136.2703 26.03143 2.47079
Independent Samples Test
Levene's Test for Equality of
Variances
t-test for Equality of Means
F Sig. t df Sig. (2-
tailed)
Mean
Difference
Std. Error
Difference
95% Confidence Interval of
the Difference
Lower Upper
SBP
Equal variances
assumed 6.391 .012 .105 213 .917 .32588 3.11614 -5.81653 6.46830
Equal variances not
assumed .106 200.406 .916 .32588 3.08439 -5.75613 6.40790
Results are reflecting that data is not normally distributed. Significance value of Shapiro Wilk test is 0.00<0.05 which means
that data is not normally distributed. Histogram chart is prepared as part of normality test and it can be observed that in case of male
there is normality in the data to some extent as curve is bell shaped but not properly shaped. In case of female category histogram is
clearly reflecting that curve is not bell shaped. Thus, it can be said that data is not normally distributed as reflected by Shapiro wilk
test.
H0: There is no significant mean difference between gender and blood pressure.
H1: There is significant mean difference between gender and blood pressure.
Group Statistics
Sex N Mean Std. Deviation Std. Error Mean
SBP Male 104 136.5962 18.82805 1.84624
Female 111 136.2703 26.03143 2.47079
Independent Samples Test
Levene's Test for Equality of
Variances
t-test for Equality of Means
F Sig. t df Sig. (2-
tailed)
Mean
Difference
Std. Error
Difference
95% Confidence Interval of
the Difference
Lower Upper
SBP
Equal variances
assumed 6.391 .012 .105 213 .917 .32588 3.11614 -5.81653 6.46830
Equal variances not
assumed .106 200.406 .916 .32588 3.08439 -5.75613 6.40790

Interpretation
In order to identify whether there is significant difference between gender and blood pressure variable independent T test are
applied on the given data set. Descriptive table is clearly indicating that for males statistics are (mean=136.59 and standard
deviation=18.82) and same for female is (mean=136.27 and standard deviation is 26.03). Other test statistic revealed in the table are
mean difference= 0.33 and 95% confidence interval value is -5.76 to 6.40. Degree of freedom is 200.40 and t statistic value is 0.106.
Degree of freedom reflects the number of values in the statistics that are allowed to vary for calculation purpose. Results are reflecting
that in the calculation only 200 values of the independent variables are allowed to very. Value of t statistic is Value of level of
significance for T test applied on variable is 0.106 and it reflect the departure of an estimated parameter from specific value. Value of
level of significance is 0.916>0.05 which means that there is no significant difference between gender and blood pressure. This
reflects that null hypothesis is accepted.
b. Determine whether there is a significant association between systolic blood pressure and BMI category. Interpret your results
Tests of Normality
BMIcat Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP
Normal .151 92 .000 .876 92 .000
Overweight .153 96 .000 .893 96 .000
Obese .181 27 .023 .868 27 .003
a. Lilliefors Significance Correction
Assumptions
In order to identify whether there is significant difference between gender and blood pressure variable independent T test are
applied on the given data set. Descriptive table is clearly indicating that for males statistics are (mean=136.59 and standard
deviation=18.82) and same for female is (mean=136.27 and standard deviation is 26.03). Other test statistic revealed in the table are
mean difference= 0.33 and 95% confidence interval value is -5.76 to 6.40. Degree of freedom is 200.40 and t statistic value is 0.106.
Degree of freedom reflects the number of values in the statistics that are allowed to vary for calculation purpose. Results are reflecting
that in the calculation only 200 values of the independent variables are allowed to very. Value of t statistic is Value of level of
significance for T test applied on variable is 0.106 and it reflect the departure of an estimated parameter from specific value. Value of
level of significance is 0.916>0.05 which means that there is no significant difference between gender and blood pressure. This
reflects that null hypothesis is accepted.
b. Determine whether there is a significant association between systolic blood pressure and BMI category. Interpret your results
Tests of Normality
BMIcat Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP
Normal .151 92 .000 .876 92 .000
Overweight .153 96 .000 .893 96 .000
Obese .181 27 .023 .868 27 .003
a. Lilliefors Significance Correction
Assumptions
There must be dependent variable in the data set in respect to hypothesis. In the present case dependent variable is blood
pressure. Independent variable consists of categorical variable which may be male or female etc. There must be independence of observations. There must be no outliers in the dataset. Data must not be normally distributed.
H0: There is no significant difference between mean value of systolic blood pressure and BMI category.
H1: There is significant difference between mean value of systolic blood pressure and BMI category.
ANOVA
SBP
Sum of Squares df Mean Square F Sig.
Between Groups 10678.517 2 5339.259 11.276 .000
Within Groups 100380.115 212 473.491
Total 111058.633 214
Post Hoc Tests
Multiple Comparisons
Dependent Variable: SBP
Tukey HSD
(I) BMIcat (J) BMIcat Mean Difference (I-
J)
Std. Error Sig. 95% Confidence Interval
Lower Bound Upper Bound
Normal Overweight -14.09239* 3.17472 .000 -21.5857 -6.5991
pressure. Independent variable consists of categorical variable which may be male or female etc. There must be independence of observations. There must be no outliers in the dataset. Data must not be normally distributed.
H0: There is no significant difference between mean value of systolic blood pressure and BMI category.
H1: There is significant difference between mean value of systolic blood pressure and BMI category.
ANOVA
SBP
Sum of Squares df Mean Square F Sig.
Between Groups 10678.517 2 5339.259 11.276 .000
Within Groups 100380.115 212 473.491
Total 111058.633 214
Post Hoc Tests
Multiple Comparisons
Dependent Variable: SBP
Tukey HSD
(I) BMIcat (J) BMIcat Mean Difference (I-
J)
Std. Error Sig. 95% Confidence Interval
Lower Bound Upper Bound
Normal Overweight -14.09239* 3.17472 .000 -21.5857 -6.5991
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Obese -14.75443* 4.76270 .006 -25.9958 -3.5130
Overweight Normal 14.09239* 3.17472 .000 6.5991 21.5857
Obese -.66204 4.74014 .989 -11.8502 10.5261
Obese Normal 14.75443* 4.76270 .006 3.5130 25.9958
Overweight .66204 4.74014 .989 -10.5261 11.8502
*. The mean difference is significant at the 0.05 level.
Homogeneous Subsets
SBP
Tukey HSD
BMIcat N Subset for alpha = 0.05
1 2
Normal 92 128.2826
Overweight 96 142.3750
Obese 27 143.0370
Sig. 1.000 .987
Means for groups in homogeneous subsets are displayed.
a. Uses Harmonic Mean Sample Size = 51.437.
b. The group sizes are unequal. The harmonic mean of the
group sizes is used. Type I error levels are not guaranteed.
Interpretation
Overweight Normal 14.09239* 3.17472 .000 6.5991 21.5857
Obese -.66204 4.74014 .989 -11.8502 10.5261
Obese Normal 14.75443* 4.76270 .006 3.5130 25.9958
Overweight .66204 4.74014 .989 -10.5261 11.8502
*. The mean difference is significant at the 0.05 level.
Homogeneous Subsets
SBP
Tukey HSD
BMIcat N Subset for alpha = 0.05
1 2
Normal 92 128.2826
Overweight 96 142.3750
Obese 27 143.0370
Sig. 1.000 .987
Means for groups in homogeneous subsets are displayed.
a. Uses Harmonic Mean Sample Size = 51.437.
b. The group sizes are unequal. The harmonic mean of the
group sizes is used. Type I error levels are not guaranteed.
Interpretation
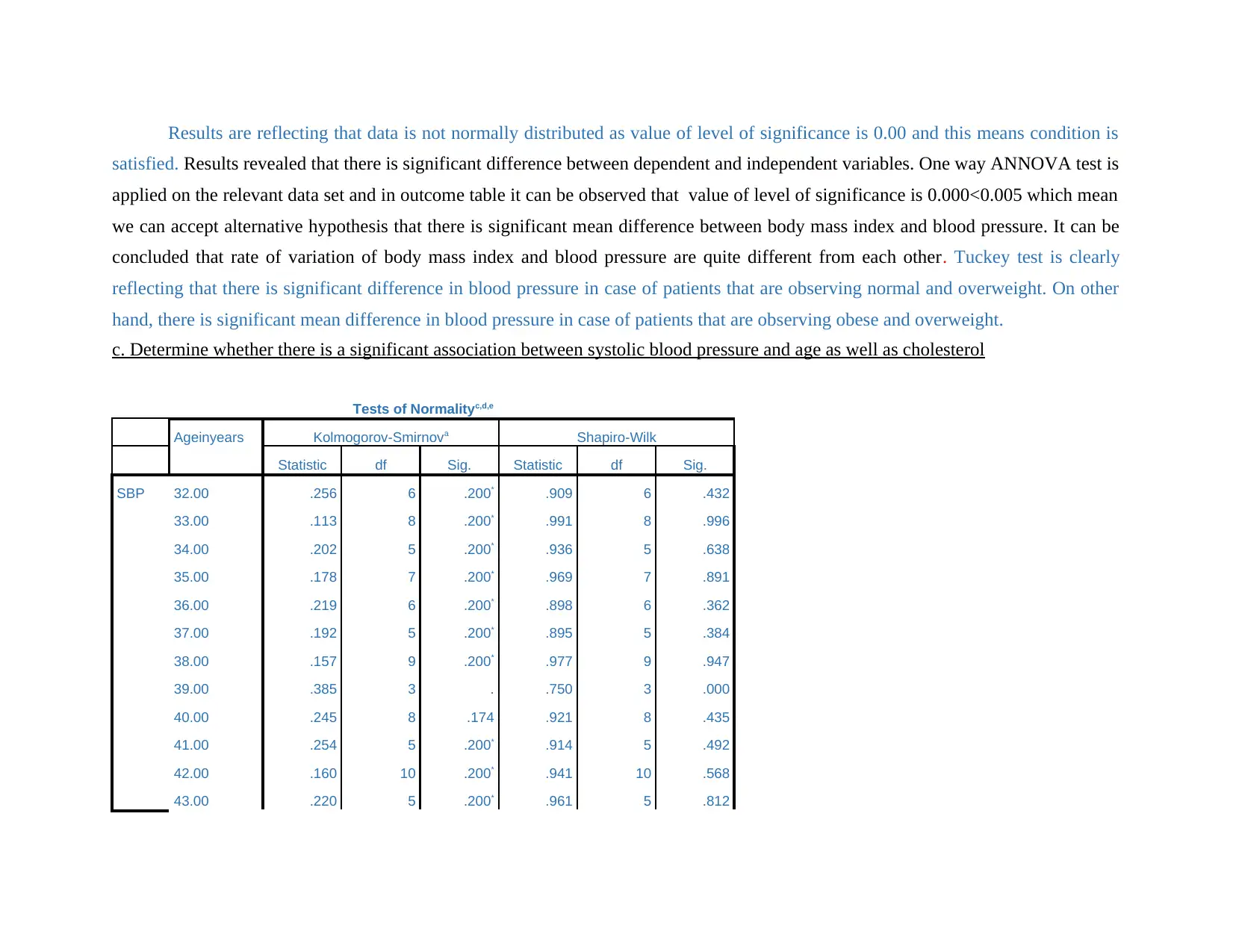
Results are reflecting that data is not normally distributed as value of level of significance is 0.00 and this means condition is
satisfied. Results revealed that there is significant difference between dependent and independent variables. One way ANNOVA test is
applied on the relevant data set and in outcome table it can be observed that value of level of significance is 0.000<0.005 which mean
we can accept alternative hypothesis that there is significant mean difference between body mass index and blood pressure. It can be
concluded that rate of variation of body mass index and blood pressure are quite different from each other. Tuckey test is clearly
reflecting that there is significant difference in blood pressure in case of patients that are observing normal and overweight. On other
hand, there is significant mean difference in blood pressure in case of patients that are observing obese and overweight.
c. Determine whether there is a significant association between systolic blood pressure and age as well as cholesterol
Tests of Normalityc,d,e
Ageinyears Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP 32.00 .256 6 .200* .909 6 .432
33.00 .113 8 .200* .991 8 .996
34.00 .202 5 .200* .936 5 .638
35.00 .178 7 .200* .969 7 .891
36.00 .219 6 .200* .898 6 .362
37.00 .192 5 .200* .895 5 .384
38.00 .157 9 .200* .977 9 .947
39.00 .385 3 . .750 3 .000
40.00 .245 8 .174 .921 8 .435
41.00 .254 5 .200* .914 5 .492
42.00 .160 10 .200* .941 10 .568
43.00 .220 5 .200* .961 5 .812
satisfied. Results revealed that there is significant difference between dependent and independent variables. One way ANNOVA test is
applied on the relevant data set and in outcome table it can be observed that value of level of significance is 0.000<0.005 which mean
we can accept alternative hypothesis that there is significant mean difference between body mass index and blood pressure. It can be
concluded that rate of variation of body mass index and blood pressure are quite different from each other. Tuckey test is clearly
reflecting that there is significant difference in blood pressure in case of patients that are observing normal and overweight. On other
hand, there is significant mean difference in blood pressure in case of patients that are observing obese and overweight.
c. Determine whether there is a significant association between systolic blood pressure and age as well as cholesterol
Tests of Normalityc,d,e
Ageinyears Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
SBP 32.00 .256 6 .200* .909 6 .432
33.00 .113 8 .200* .991 8 .996
34.00 .202 5 .200* .936 5 .638
35.00 .178 7 .200* .969 7 .891
36.00 .219 6 .200* .898 6 .362
37.00 .192 5 .200* .895 5 .384
38.00 .157 9 .200* .977 9 .947
39.00 .385 3 . .750 3 .000
40.00 .245 8 .174 .921 8 .435
41.00 .254 5 .200* .914 5 .492
42.00 .160 10 .200* .941 10 .568
43.00 .220 5 .200* .961 5 .812
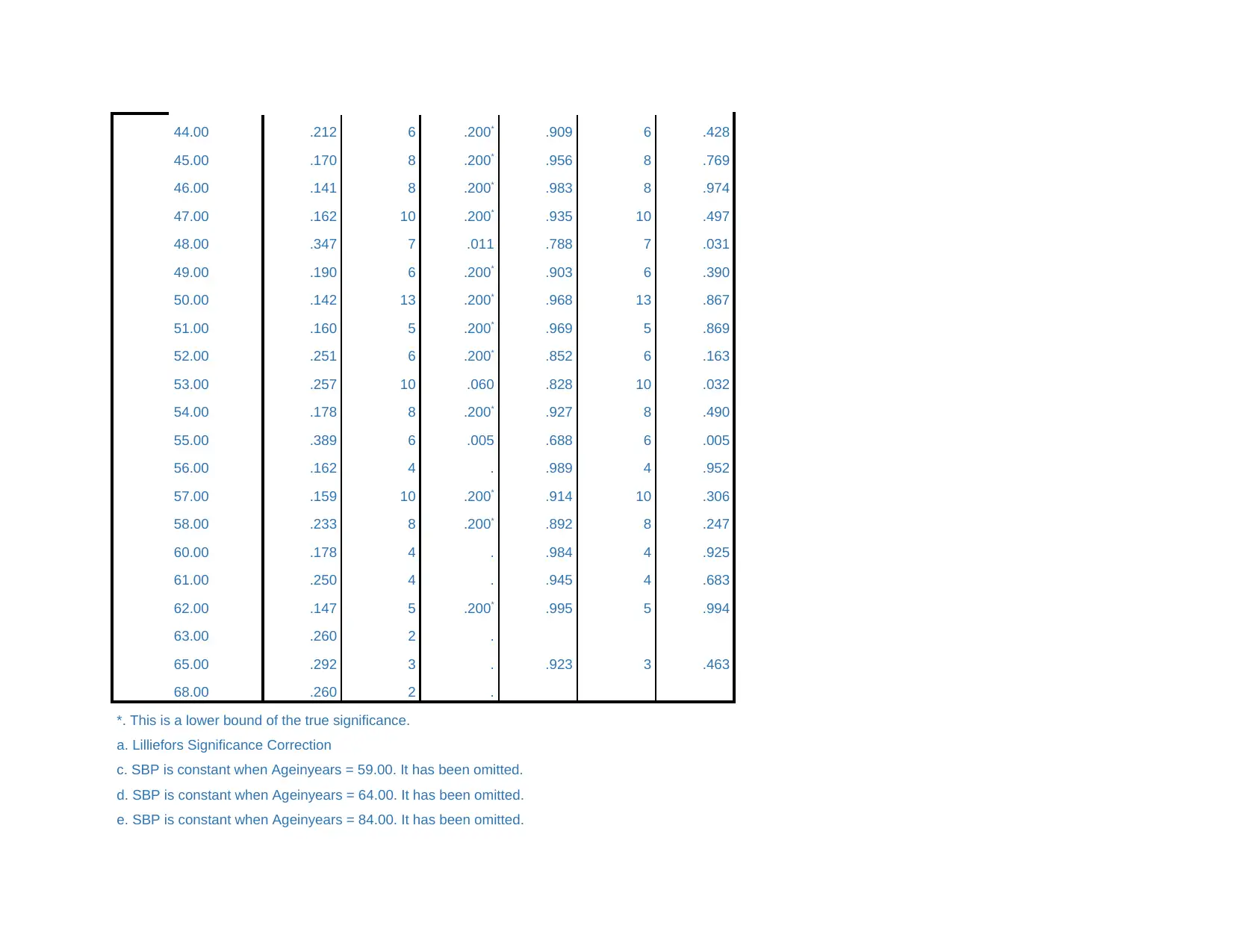
44.00 .212 6 .200* .909 6 .428
45.00 .170 8 .200* .956 8 .769
46.00 .141 8 .200* .983 8 .974
47.00 .162 10 .200* .935 10 .497
48.00 .347 7 .011 .788 7 .031
49.00 .190 6 .200* .903 6 .390
50.00 .142 13 .200* .968 13 .867
51.00 .160 5 .200* .969 5 .869
52.00 .251 6 .200* .852 6 .163
53.00 .257 10 .060 .828 10 .032
54.00 .178 8 .200* .927 8 .490
55.00 .389 6 .005 .688 6 .005
56.00 .162 4 . .989 4 .952
57.00 .159 10 .200* .914 10 .306
58.00 .233 8 .200* .892 8 .247
60.00 .178 4 . .984 4 .925
61.00 .250 4 . .945 4 .683
62.00 .147 5 .200* .995 5 .994
63.00 .260 2 .
65.00 .292 3 . .923 3 .463
68.00 .260 2 .
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
c. SBP is constant when Ageinyears = 59.00. It has been omitted.
d. SBP is constant when Ageinyears = 64.00. It has been omitted.
e. SBP is constant when Ageinyears = 84.00. It has been omitted.
45.00 .170 8 .200* .956 8 .769
46.00 .141 8 .200* .983 8 .974
47.00 .162 10 .200* .935 10 .497
48.00 .347 7 .011 .788 7 .031
49.00 .190 6 .200* .903 6 .390
50.00 .142 13 .200* .968 13 .867
51.00 .160 5 .200* .969 5 .869
52.00 .251 6 .200* .852 6 .163
53.00 .257 10 .060 .828 10 .032
54.00 .178 8 .200* .927 8 .490
55.00 .389 6 .005 .688 6 .005
56.00 .162 4 . .989 4 .952
57.00 .159 10 .200* .914 10 .306
58.00 .233 8 .200* .892 8 .247
60.00 .178 4 . .984 4 .925
61.00 .250 4 . .945 4 .683
62.00 .147 5 .200* .995 5 .994
63.00 .260 2 .
65.00 .292 3 . .923 3 .463
68.00 .260 2 .
*. This is a lower bound of the true significance.
a. Lilliefors Significance Correction
c. SBP is constant when Ageinyears = 59.00. It has been omitted.
d. SBP is constant when Ageinyears = 64.00. It has been omitted.
e. SBP is constant when Ageinyears = 84.00. It has been omitted.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Assumptions of correlation
There must be normality in data or facts that are analyzed must be normally distributed.
There must be linearity among the variables.
There should be homoscedasticity in the analyzed variables.
Age
H0: There is not significant relationship between SBP and age factor
H1: There is significant relationship between SBP and age factor
Correlations
SBP Ageinyears
SBP
Pearson Correlation 1 .474**
Sig. (2-tailed) .000
N 215 215
Ageinyears
Pearson Correlation .474** 1
Sig. (2-tailed) .000
N 215 215
**. Correlation is significant at the 0.01 level (2-tailed).
Interpretation
Komorov test is reflecting that data is normally distributed as value of level of significance in most cases is nearby to
0.200>0.05. Hence, it can be said that condition is satisfied for correlation. From the outcome table given above it can be observed
There must be normality in data or facts that are analyzed must be normally distributed.
There must be linearity among the variables.
There should be homoscedasticity in the analyzed variables.
Age
H0: There is not significant relationship between SBP and age factor
H1: There is significant relationship between SBP and age factor
Correlations
SBP Ageinyears
SBP
Pearson Correlation 1 .474**
Sig. (2-tailed) .000
N 215 215
Ageinyears
Pearson Correlation .474** 1
Sig. (2-tailed) .000
N 215 215
**. Correlation is significant at the 0.01 level (2-tailed).
Interpretation
Komorov test is reflecting that data is normally distributed as value of level of significance in most cases is nearby to
0.200>0.05. Hence, it can be said that condition is satisfied for correlation. From the outcome table given above it can be observed
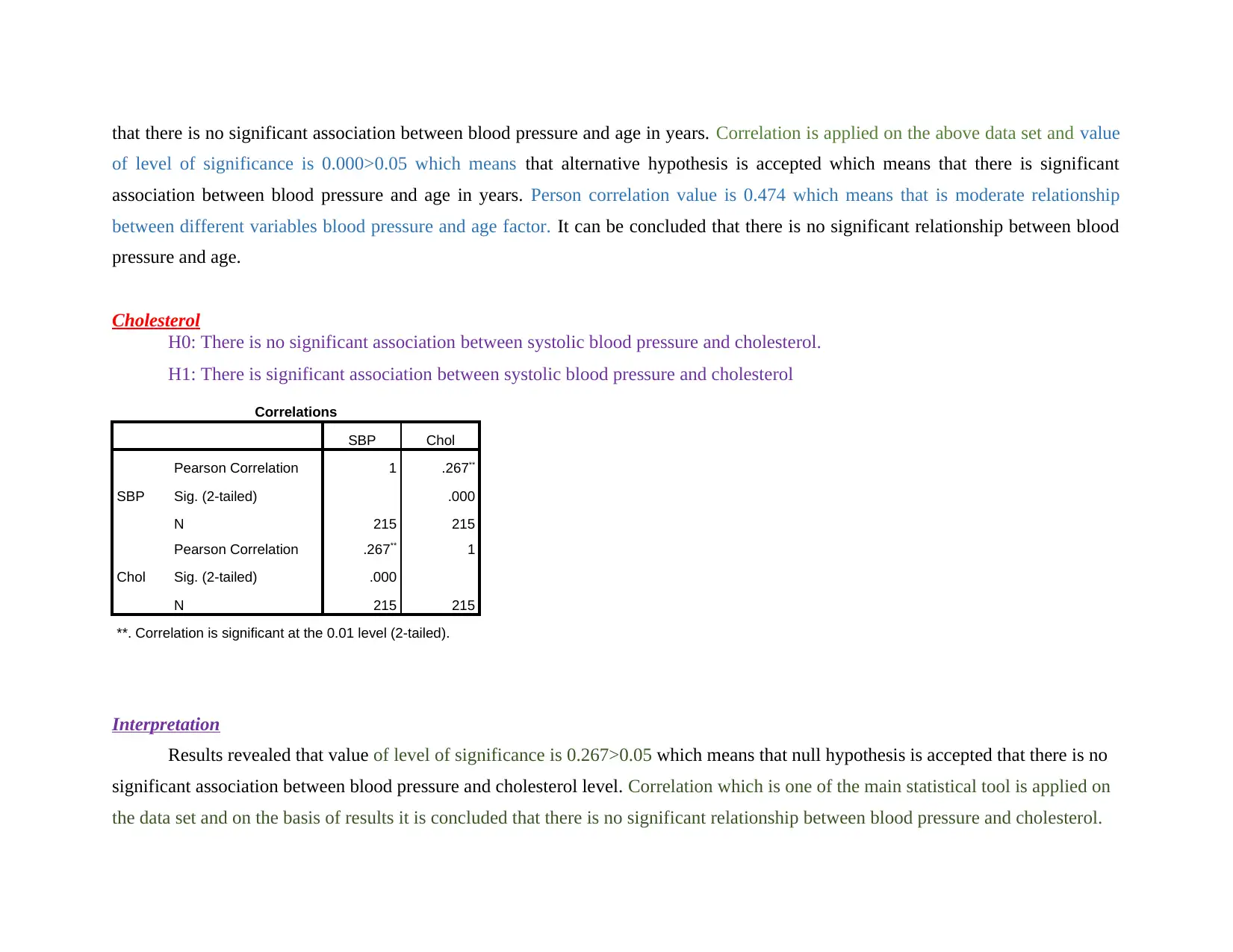
that there is no significant association between blood pressure and age in years. Correlation is applied on the above data set and value
of level of significance is 0.000>0.05 which means that alternative hypothesis is accepted which means that there is significant
association between blood pressure and age in years. Person correlation value is 0.474 which means that is moderate relationship
between different variables blood pressure and age factor. It can be concluded that there is no significant relationship between blood
pressure and age.
Cholesterol
H0: There is no significant association between systolic blood pressure and cholesterol.
H1: There is significant association between systolic blood pressure and cholesterol
Correlations
SBP Chol
SBP
Pearson Correlation 1 .267**
Sig. (2-tailed) .000
N 215 215
Chol
Pearson Correlation .267** 1
Sig. (2-tailed) .000
N 215 215
**. Correlation is significant at the 0.01 level (2-tailed).
Interpretation
Results revealed that value of level of significance is 0.267>0.05 which means that null hypothesis is accepted that there is no
significant association between blood pressure and cholesterol level. Correlation which is one of the main statistical tool is applied on
the data set and on the basis of results it is concluded that there is no significant relationship between blood pressure and cholesterol.
of level of significance is 0.000>0.05 which means that alternative hypothesis is accepted which means that there is significant
association between blood pressure and age in years. Person correlation value is 0.474 which means that is moderate relationship
between different variables blood pressure and age factor. It can be concluded that there is no significant relationship between blood
pressure and age.
Cholesterol
H0: There is no significant association between systolic blood pressure and cholesterol.
H1: There is significant association between systolic blood pressure and cholesterol
Correlations
SBP Chol
SBP
Pearson Correlation 1 .267**
Sig. (2-tailed) .000
N 215 215
Chol
Pearson Correlation .267** 1
Sig. (2-tailed) .000
N 215 215
**. Correlation is significant at the 0.01 level (2-tailed).
Interpretation
Results revealed that value of level of significance is 0.267>0.05 which means that null hypothesis is accepted that there is no
significant association between blood pressure and cholesterol level. Correlation which is one of the main statistical tool is applied on
the data set and on the basis of results it is concluded that there is no significant relationship between blood pressure and cholesterol.

This means that it is not necessary that if blood pressure will increase then in that case cholesterol level will also elevate in human
body.
(d) Association of variables with blood pressure
Assumptions of linear regression
There must be linear relationship among the dependent and independent variable.
There must be no or little multicolinearity among the variables in the data set.
There must be non-autocorrelation among the variables on which regression is applied.
H0: There is no significant difference between mean values of BMI and age in years as well as cholesterol level.
H1: There is no significant difference between mean values of BMI and age in years as well as cholesterol level.
Variables Entered/Removeda
Model Variables Entered Variables
Removed
Method
1 BMIcat,
Ageinyears, Cholb . Enter
a. Dependent Variable: SBP
b. All requested variables entered.
Model Summary
Model R R Square Adjusted R Square Std. Error of the
Estimate
1 .520a .270 .260 19.60004
a. Predictors: (Constant), BMIcat, Ageinyears, Chol
body.
(d) Association of variables with blood pressure
Assumptions of linear regression
There must be linear relationship among the dependent and independent variable.
There must be no or little multicolinearity among the variables in the data set.
There must be non-autocorrelation among the variables on which regression is applied.
H0: There is no significant difference between mean values of BMI and age in years as well as cholesterol level.
H1: There is no significant difference between mean values of BMI and age in years as well as cholesterol level.
Variables Entered/Removeda
Model Variables Entered Variables
Removed
Method
1 BMIcat,
Ageinyears, Cholb . Enter
a. Dependent Variable: SBP
b. All requested variables entered.
Model Summary
Model R R Square Adjusted R Square Std. Error of the
Estimate
1 .520a .270 .260 19.60004
a. Predictors: (Constant), BMIcat, Ageinyears, Chol
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
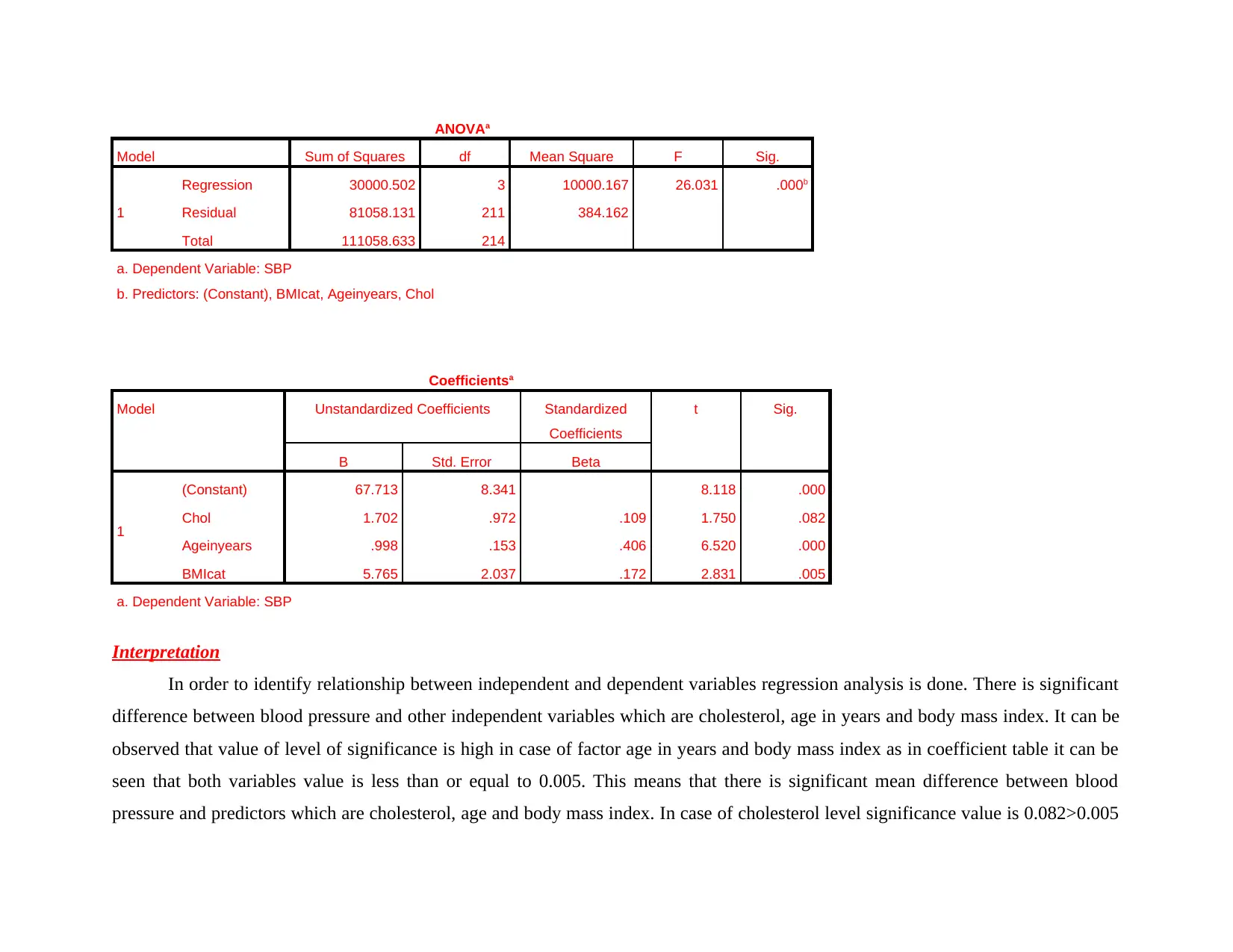
ANOVAa
Model Sum of Squares df Mean Square F Sig.
1
Regression 30000.502 3 10000.167 26.031 .000b
Residual 81058.131 211 384.162
Total 111058.633 214
a. Dependent Variable: SBP
b. Predictors: (Constant), BMIcat, Ageinyears, Chol
Coefficientsa
Model Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
1
(Constant) 67.713 8.341 8.118 .000
Chol 1.702 .972 .109 1.750 .082
Ageinyears .998 .153 .406 6.520 .000
BMIcat 5.765 2.037 .172 2.831 .005
a. Dependent Variable: SBP
Interpretation
In order to identify relationship between independent and dependent variables regression analysis is done. There is significant
difference between blood pressure and other independent variables which are cholesterol, age in years and body mass index. It can be
observed that value of level of significance is high in case of factor age in years and body mass index as in coefficient table it can be
seen that both variables value is less than or equal to 0.005. This means that there is significant mean difference between blood
pressure and predictors which are cholesterol, age and body mass index. In case of cholesterol level significance value is 0.082>0.005
Model Sum of Squares df Mean Square F Sig.
1
Regression 30000.502 3 10000.167 26.031 .000b
Residual 81058.131 211 384.162
Total 111058.633 214
a. Dependent Variable: SBP
b. Predictors: (Constant), BMIcat, Ageinyears, Chol
Coefficientsa
Model Unstandardized Coefficients Standardized
Coefficients
t Sig.
B Std. Error Beta
1
(Constant) 67.713 8.341 8.118 .000
Chol 1.702 .972 .109 1.750 .082
Ageinyears .998 .153 .406 6.520 .000
BMIcat 5.765 2.037 .172 2.831 .005
a. Dependent Variable: SBP
Interpretation
In order to identify relationship between independent and dependent variables regression analysis is done. There is significant
difference between blood pressure and other independent variables which are cholesterol, age in years and body mass index. It can be
observed that value of level of significance is high in case of factor age in years and body mass index as in coefficient table it can be
seen that both variables value is less than or equal to 0.005. This means that there is significant mean difference between blood
pressure and predictors which are cholesterol, age and body mass index. In case of cholesterol level significance value is 0.082>0.005

and it can be said that it is cholesterol level that does not have big impact on the blood pressure in human body. R square value is
0.270 which means that there is low correlation among the variables which are blood pressure and independent variables which are
body mass index, age in years and cholesterol level. It can be said that with change in independent variable change come in dependent
variable. Value of R is 0.52 which reflects that with change in variables cholesterol, body mass index and age in years 52% change
comes in the blood pressure. Results are clearly reflecting that age factor and body mass index are the major predictor of the blood
pressure in human body as value of level of significance of both is equal or less then alpha value 0.05. This also means that in
comparison to cholesterol level (0.082>0.05) with change in age (0.00>0.05) and body mass index (0.005<0.05) blood pressure is
heavily affected in case of relevant patients.
Question 2
(a)Relationship between coronary heart disease and BMI category as well as gender
H0: There is no significant association between BMI and coronary health disease.
H1: There is significant association between BMI and coronary health disease.
BMI category
Case Processing Summary
Cases
Valid Missing Total
N Percent N Percent N Percent
CHD * BMIcat 215 100.0% 0 0.0% 215 100.0%
CHD * BMIcat Crosstabulation
0.270 which means that there is low correlation among the variables which are blood pressure and independent variables which are
body mass index, age in years and cholesterol level. It can be said that with change in independent variable change come in dependent
variable. Value of R is 0.52 which reflects that with change in variables cholesterol, body mass index and age in years 52% change
comes in the blood pressure. Results are clearly reflecting that age factor and body mass index are the major predictor of the blood
pressure in human body as value of level of significance of both is equal or less then alpha value 0.05. This also means that in
comparison to cholesterol level (0.082>0.05) with change in age (0.00>0.05) and body mass index (0.005<0.05) blood pressure is
heavily affected in case of relevant patients.
Question 2
(a)Relationship between coronary heart disease and BMI category as well as gender
H0: There is no significant association between BMI and coronary health disease.
H1: There is significant association between BMI and coronary health disease.
BMI category
Case Processing Summary
Cases
Valid Missing Total
N Percent N Percent N Percent
CHD * BMIcat 215 100.0% 0 0.0% 215 100.0%
CHD * BMIcat Crosstabulation
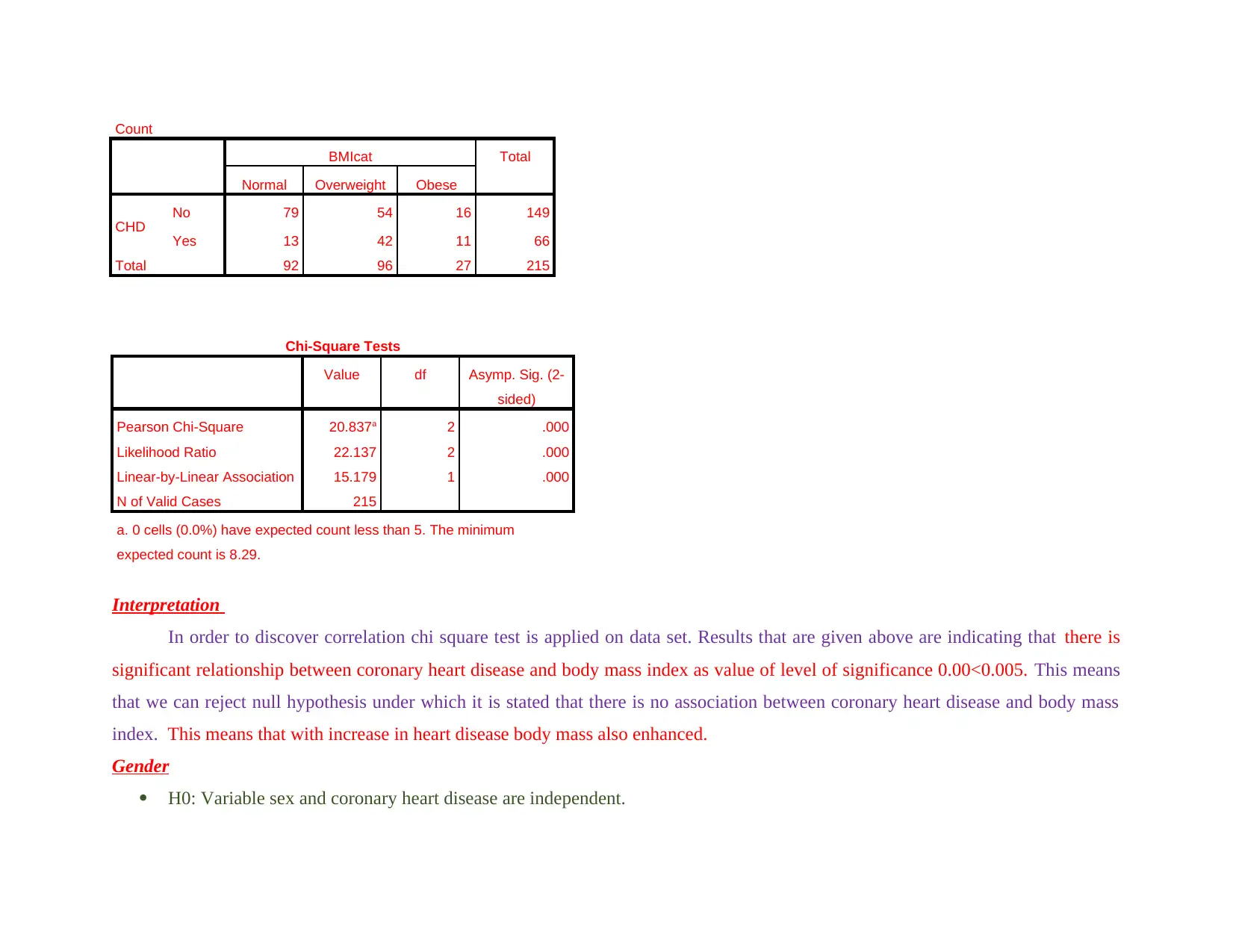
Count
BMIcat Total
Normal Overweight Obese
CHD No 79 54 16 149
Yes 13 42 11 66
Total 92 96 27 215
Chi-Square Tests
Value df Asymp. Sig. (2-
sided)
Pearson Chi-Square 20.837a 2 .000
Likelihood Ratio 22.137 2 .000
Linear-by-Linear Association 15.179 1 .000
N of Valid Cases 215
a. 0 cells (0.0%) have expected count less than 5. The minimum
expected count is 8.29.
Interpretation
In order to discover correlation chi square test is applied on data set. Results that are given above are indicating that there is
significant relationship between coronary heart disease and body mass index as value of level of significance 0.00<0.005. This means
that we can reject null hypothesis under which it is stated that there is no association between coronary heart disease and body mass
index. This means that with increase in heart disease body mass also enhanced.
Gender
H0: Variable sex and coronary heart disease are independent.
BMIcat Total
Normal Overweight Obese
CHD No 79 54 16 149
Yes 13 42 11 66
Total 92 96 27 215
Chi-Square Tests
Value df Asymp. Sig. (2-
sided)
Pearson Chi-Square 20.837a 2 .000
Likelihood Ratio 22.137 2 .000
Linear-by-Linear Association 15.179 1 .000
N of Valid Cases 215
a. 0 cells (0.0%) have expected count less than 5. The minimum
expected count is 8.29.
Interpretation
In order to discover correlation chi square test is applied on data set. Results that are given above are indicating that there is
significant relationship between coronary heart disease and body mass index as value of level of significance 0.00<0.005. This means
that we can reject null hypothesis under which it is stated that there is no association between coronary heart disease and body mass
index. This means that with increase in heart disease body mass also enhanced.
Gender
H0: Variable sex and coronary heart disease are independent.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

H1: Variable sex and coronary heart disease are not independent.
Case Processing Summary
Cases
Valid Missing Total
N Percent N Percent N Percent
CHD * Sex 215 100.0% 0 0.0% 215 100.0%
CHD * Sex Crosstabulation
Count
Sex Total
Male Female
CHD No 66 83 149
Yes 38 28 66
Total 104 111 215
Chi-Square Tests
Value df Asymp. Sig. (2-
sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 3.230a 1 .072
Continuity Correctionb 2.720 1 .099
Likelihood Ratio 3.237 1 .072
Fisher's Exact Test .078 .049
Linear-by-Linear Association 3.215 1 .073
N of Valid Cases 215
Case Processing Summary
Cases
Valid Missing Total
N Percent N Percent N Percent
CHD * Sex 215 100.0% 0 0.0% 215 100.0%
CHD * Sex Crosstabulation
Count
Sex Total
Male Female
CHD No 66 83 149
Yes 38 28 66
Total 104 111 215
Chi-Square Tests
Value df Asymp. Sig. (2-
sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 3.230a 1 .072
Continuity Correctionb 2.720 1 .099
Likelihood Ratio 3.237 1 .072
Fisher's Exact Test .078 .049
Linear-by-Linear Association 3.215 1 .073
N of Valid Cases 215

a. 0 cells (0.0%) have expected count less than 5. The minimum expected count is 31.93.
b. Computed only for a 2x2 table
Interpretation
Assumptions are fulfilled in the current calculation. It can be observed that in the calculation categorical variable is used like
male and female which are independent in nature. In this way assumption of chi square test is fulfilled. Results are indicating that
level of significance is 0.072>0.05 which reflects that there is no significant association between coronary heart disease and gender
groups. This means that that null hypothesis is accepted under which it was claimed that there is no significant association between
heart disease and gender factor. In case of coronary heart disease male deny from accepting asked statement (66) and female (83). On
other hand, there males (38) that accept the fact that they are suffered from heart disease followed by female (28). It can be said that
there is significant relationship between heart disease that is observed in case of male and female. This means that heart disease can
happened to male and female and there is no association between both in terms of frequency at which both gender group suffered from
heart disease.
(b) Logistic regression
H0: There is no significant mean difference between coronary heart disease and other independent variables.
H1: There is significant mean difference between coronary heart disease and other independent variables
b. Computed only for a 2x2 table
Interpretation
Assumptions are fulfilled in the current calculation. It can be observed that in the calculation categorical variable is used like
male and female which are independent in nature. In this way assumption of chi square test is fulfilled. Results are indicating that
level of significance is 0.072>0.05 which reflects that there is no significant association between coronary heart disease and gender
groups. This means that that null hypothesis is accepted under which it was claimed that there is no significant association between
heart disease and gender factor. In case of coronary heart disease male deny from accepting asked statement (66) and female (83). On
other hand, there males (38) that accept the fact that they are suffered from heart disease followed by female (28). It can be said that
there is significant relationship between heart disease that is observed in case of male and female. This means that heart disease can
happened to male and female and there is no association between both in terms of frequency at which both gender group suffered from
heart disease.
(b) Logistic regression
H0: There is no significant mean difference between coronary heart disease and other independent variables.
H1: There is significant mean difference between coronary heart disease and other independent variables
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

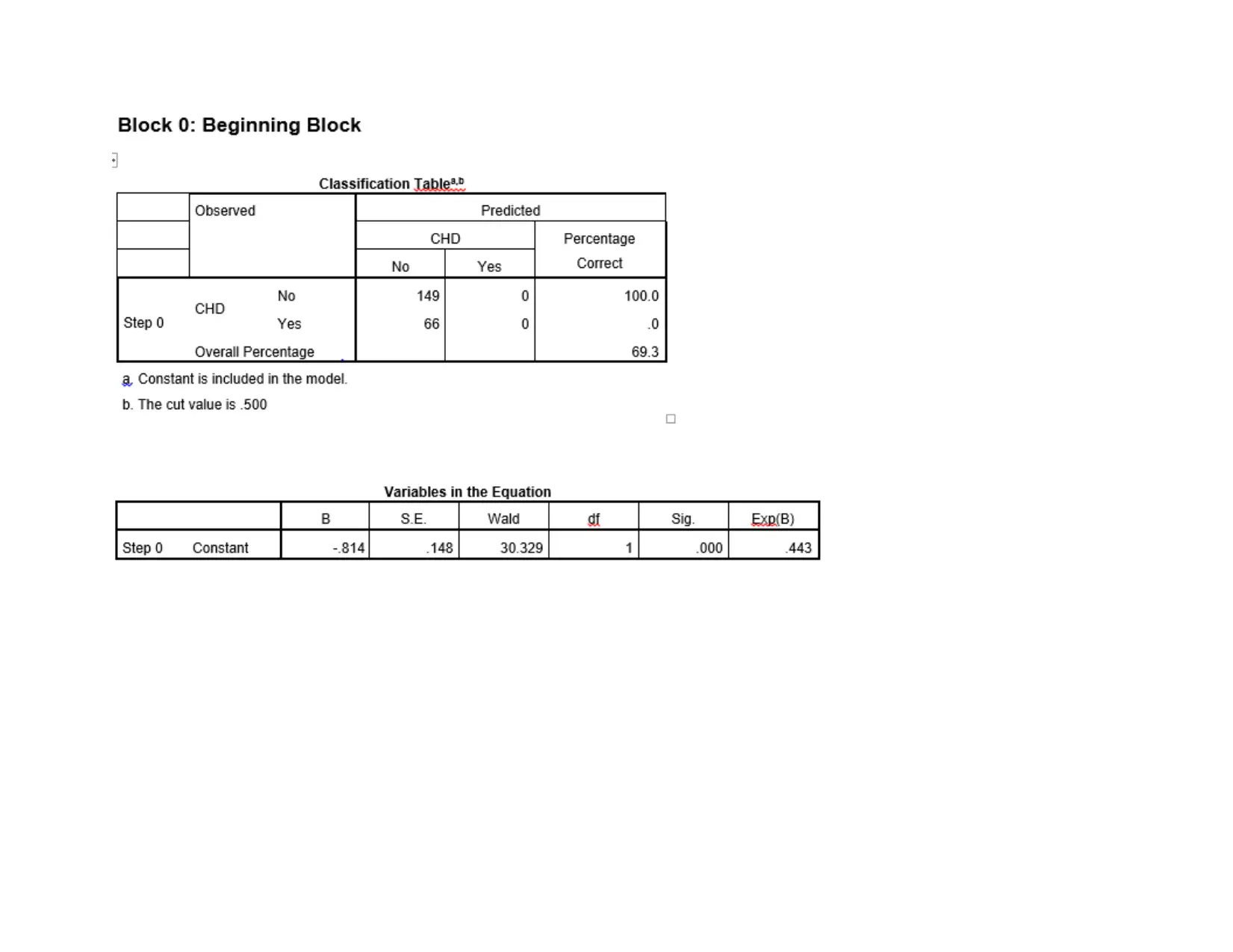
Interpretation
Results are reflecting that there is significant difference in case of most of variables except 0.072 which is identified in case of
sex variable. This means that there is significant difference between other variables namely BMI, Age, cholesterol and SBP.
Results are reflecting that there is significant difference in case of most of variables except 0.072 which is identified in case of
sex variable. This means that there is significant difference between other variables namely BMI, Age, cholesterol and SBP.
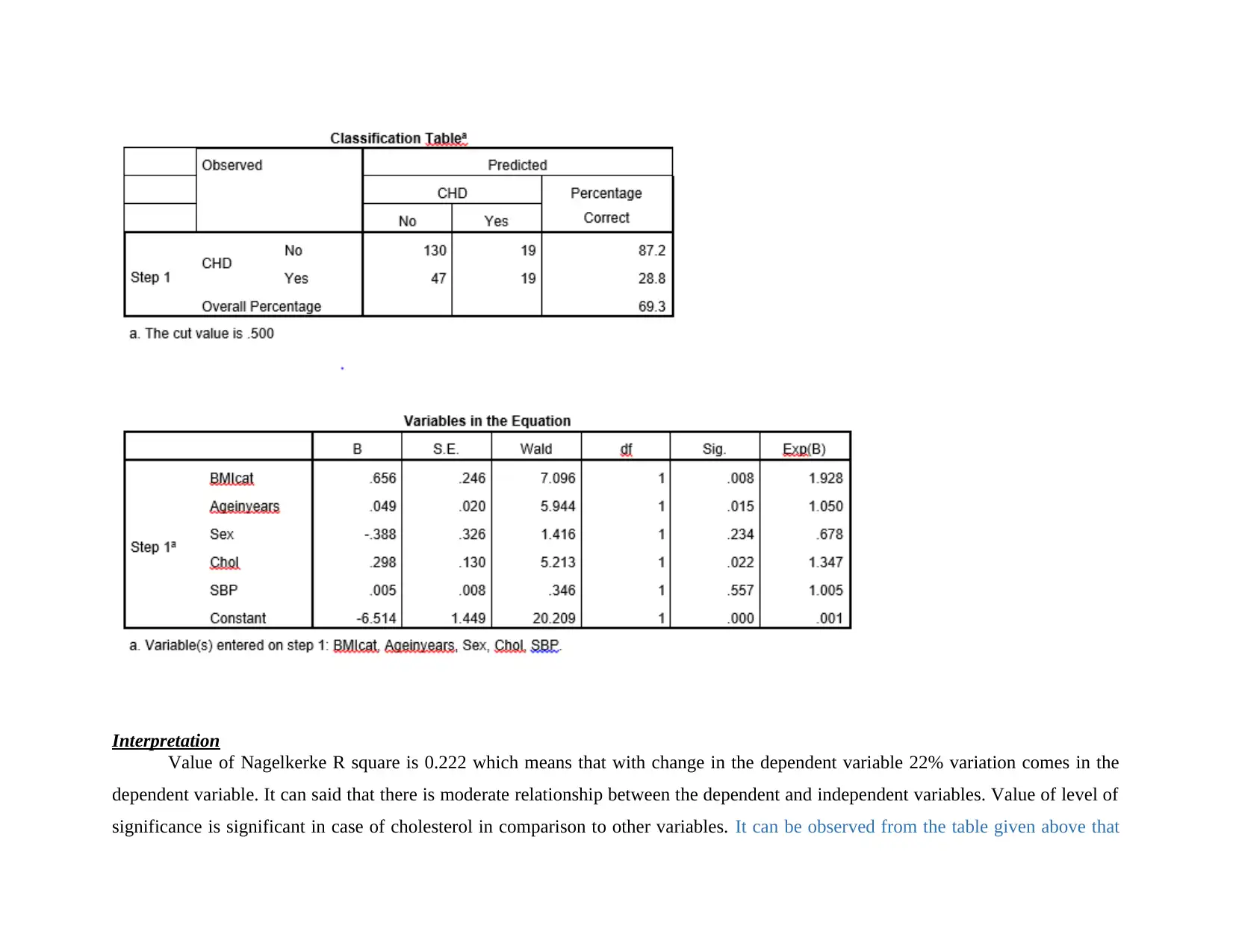
Interpretation
Value of Nagelkerke R square is 0.222 which means that with change in the dependent variable 22% variation comes in the
dependent variable. It can said that there is moderate relationship between the dependent and independent variables. Value of level of
significance is significant in case of cholesterol in comparison to other variables. It can be observed from the table given above that
Value of Nagelkerke R square is 0.222 which means that with change in the dependent variable 22% variation comes in the
dependent variable. It can said that there is moderate relationship between the dependent and independent variables. Value of level of
significance is significant in case of cholesterol in comparison to other variables. It can be observed from the table given above that

value of level of significance is (0.015>0.05) in case of age in years and same in case of cholesterol is (0.022<0.05) which reflect that
there is significant mean difference between dependent variable which is coronary heart disease and factor age in years as well as
cholesterol level. It can be said that coefficient of the mentioned variable is statistically different in comparison to other variables. Odd
ratio value for body mass index is 1.928 and same for age in years is 1.050. This reflect that with change in the body mass index
coronary heart disease change by 1.928 points and CHD change by 1.050 points with change in age factor. With variation in
cholesterol and blood pressure CHD change by 1.347 and 1.005. It can be said that nearby changes comes with slight change in
independent variables on CHD.
Question 3
A. Carry out a Kaplan-Meier survival analysis
Assumptions of Kalpan Meirer survival analysis
Event status include two mutually exclusive and collectively exhaustive states.
Time to event must be clearly defined.
There must be independence of censoring and event.
H0: There is no difference between mean values of male and female.
H1: There is difference between mean values of male and female.
Overall Comparisons
Chi-Square df Sig.
Log Rank (Mantel-Cox) 5.169 1 .023
Breslow (Generalized
Wilcoxon) 5.423 1 .020
Tarone-Ware 5.375 1 .020
Test of equality of survival distributions for the different levels of Sex.
there is significant mean difference between dependent variable which is coronary heart disease and factor age in years as well as
cholesterol level. It can be said that coefficient of the mentioned variable is statistically different in comparison to other variables. Odd
ratio value for body mass index is 1.928 and same for age in years is 1.050. This reflect that with change in the body mass index
coronary heart disease change by 1.928 points and CHD change by 1.050 points with change in age factor. With variation in
cholesterol and blood pressure CHD change by 1.347 and 1.005. It can be said that nearby changes comes with slight change in
independent variables on CHD.
Question 3
A. Carry out a Kaplan-Meier survival analysis
Assumptions of Kalpan Meirer survival analysis
Event status include two mutually exclusive and collectively exhaustive states.
Time to event must be clearly defined.
There must be independence of censoring and event.
H0: There is no difference between mean values of male and female.
H1: There is difference between mean values of male and female.
Overall Comparisons
Chi-Square df Sig.
Log Rank (Mantel-Cox) 5.169 1 .023
Breslow (Generalized
Wilcoxon) 5.423 1 .020
Tarone-Ware 5.375 1 .020
Test of equality of survival distributions for the different levels of Sex.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

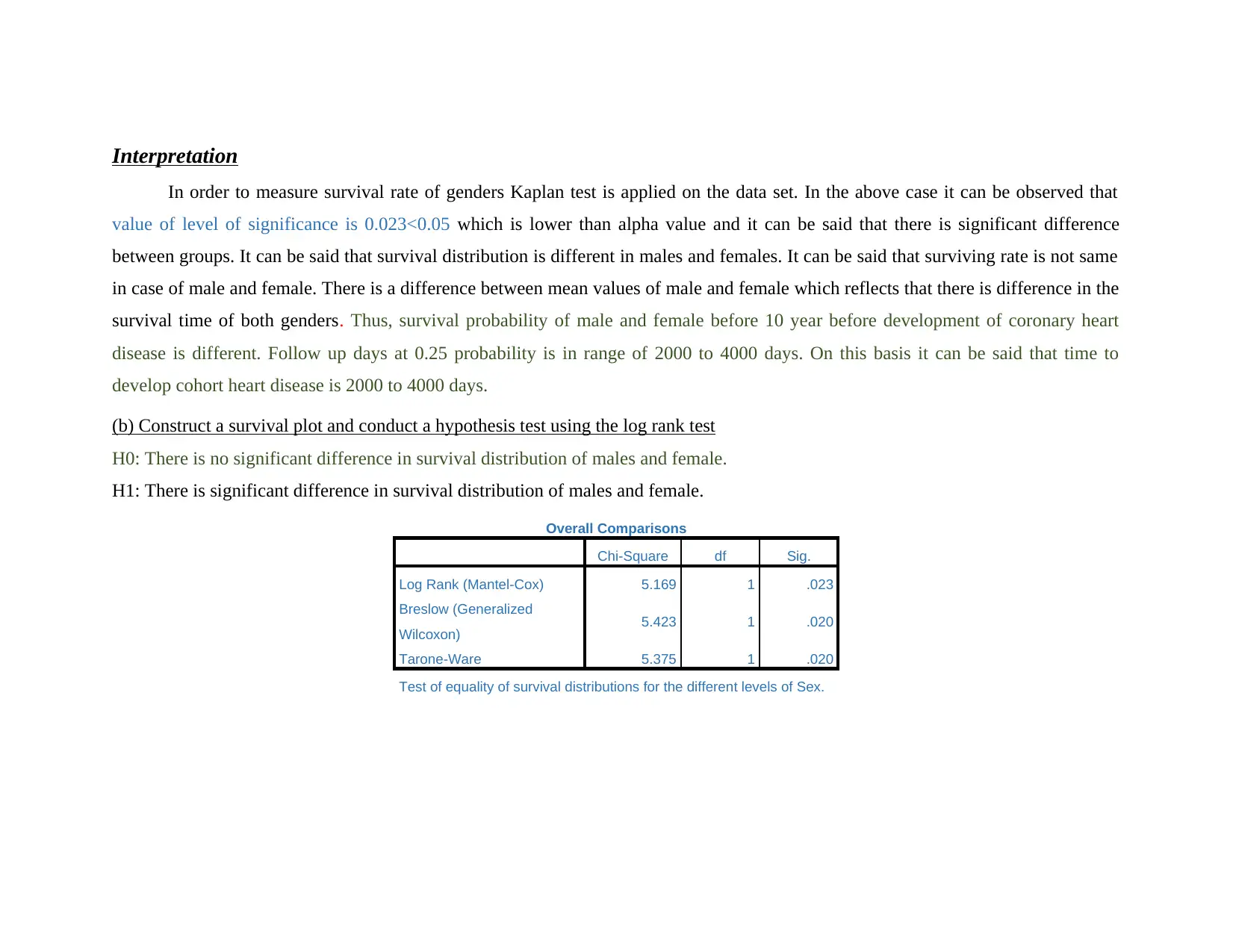
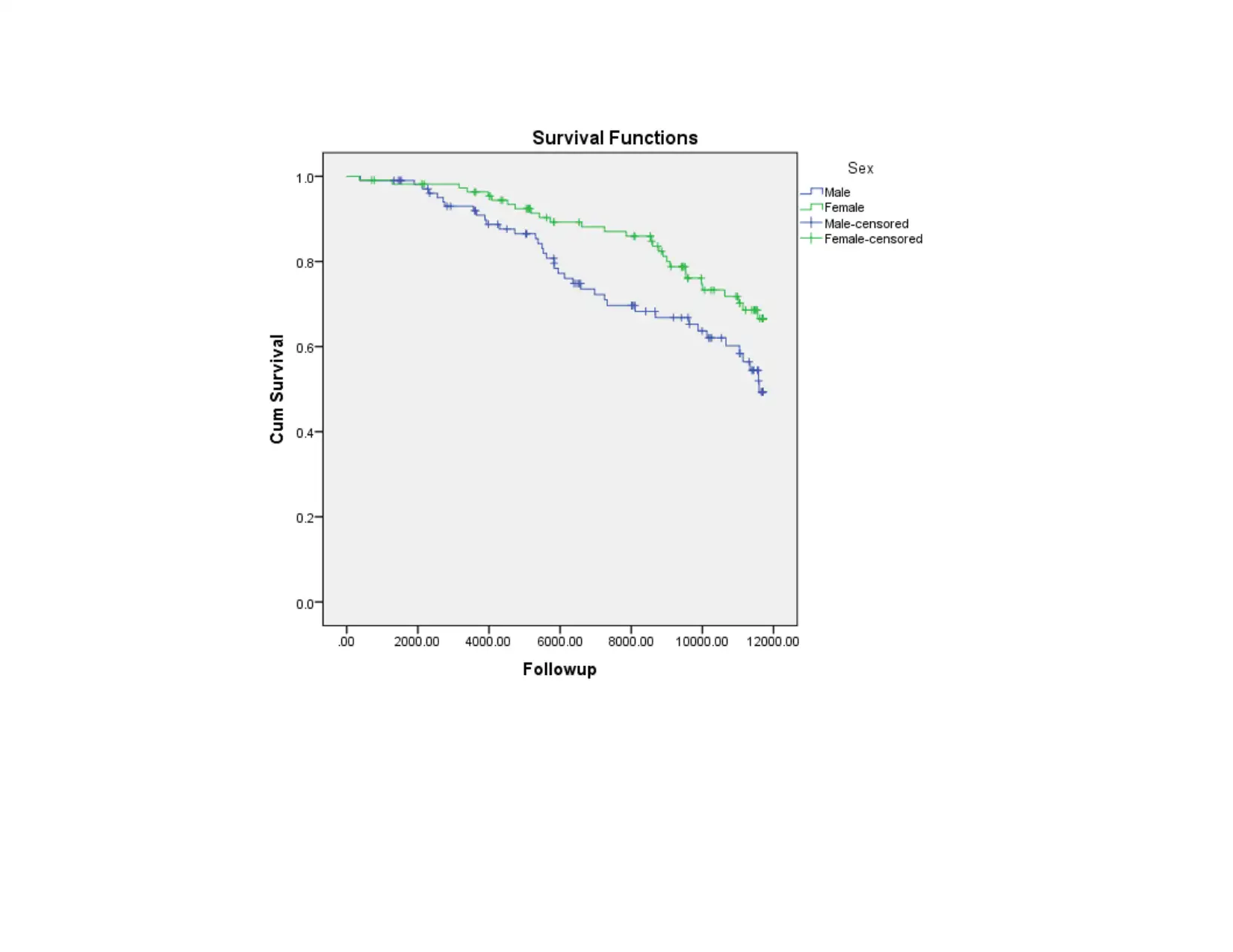
Interpretation
In order to measure survival rate of genders Kaplan test is applied on the data set. In the above case it can be observed that
value of level of significance is 0.023<0.05 which is lower than alpha value and it can be said that there is significant difference
between groups. It can be said that survival distribution is different in males and females. It can be said that surviving rate is not same
in case of male and female. There is a difference between mean values of male and female which reflects that there is difference in the
survival time of both genders. Thus, survival probability of male and female before 10 year before development of coronary heart
disease is different. Follow up days at 0.25 probability is in range of 2000 to 4000 days. On this basis it can be said that time to
develop cohort heart disease is 2000 to 4000 days.
(b) Construct a survival plot and conduct a hypothesis test using the log rank test
H0: There is no significant difference in survival distribution of males and female.
H1: There is significant difference in survival distribution of males and female.
Overall Comparisons
Chi-Square df Sig.
Log Rank (Mantel-Cox) 5.169 1 .023
Breslow (Generalized
Wilcoxon) 5.423 1 .020
Tarone-Ware 5.375 1 .020
Test of equality of survival distributions for the different levels of Sex.
In order to measure survival rate of genders Kaplan test is applied on the data set. In the above case it can be observed that
value of level of significance is 0.023<0.05 which is lower than alpha value and it can be said that there is significant difference
between groups. It can be said that survival distribution is different in males and females. It can be said that surviving rate is not same
in case of male and female. There is a difference between mean values of male and female which reflects that there is difference in the
survival time of both genders. Thus, survival probability of male and female before 10 year before development of coronary heart
disease is different. Follow up days at 0.25 probability is in range of 2000 to 4000 days. On this basis it can be said that time to
develop cohort heart disease is 2000 to 4000 days.
(b) Construct a survival plot and conduct a hypothesis test using the log rank test
H0: There is no significant difference in survival distribution of males and female.
H1: There is significant difference in survival distribution of males and female.
Overall Comparisons
Chi-Square df Sig.
Log Rank (Mantel-Cox) 5.169 1 .023
Breslow (Generalized
Wilcoxon) 5.423 1 .020
Tarone-Ware 5.375 1 .020
Test of equality of survival distributions for the different levels of Sex.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Interpretation
Time to develop coronary heart disease is not different in case of males and females. It can be observed that level of
significance is not different in case of males and females as its value is 0.02>0.05 which means that time to develop coronary heart
disease in terms is different in case of various categories of gender which are males and females. It can be said that there is no
difference in time to develop coronary heart disease for the males and females that are suffered from the heart disease.
© Cox regression
H0: There is no significant mean difference between CHD and other independent variables.
H1: There is significant mean difference between CHD and other independent variables.
Variables in the Equation
B SE Wald df Sig. Exp(B) 95.0% CI for Exp(B)
Lower Upper
Sex .328 .263 1.557 1 .212 1.388 .829 2.324
BMIcat 9.129 2 .010
BMIcat(1) -.666 .420 2.517 1 .113 .514 .226 1.170
BMIcat(2) .328 .344 .909 1 .340 1.388 .707 2.725
SBP .010 .006 2.826 1 .093 1.010 .998 1.022
Chol .255 .106 5.767 1 .016 1.290 1.048 1.588
Ageinyears .042 .014 9.315 1 .002 1.042 1.015 1.071
Time to develop coronary heart disease is not different in case of males and females. It can be observed that level of
significance is not different in case of males and females as its value is 0.02>0.05 which means that time to develop coronary heart
disease in terms is different in case of various categories of gender which are males and females. It can be said that there is no
difference in time to develop coronary heart disease for the males and females that are suffered from the heart disease.
© Cox regression
H0: There is no significant mean difference between CHD and other independent variables.
H1: There is significant mean difference between CHD and other independent variables.
Variables in the Equation
B SE Wald df Sig. Exp(B) 95.0% CI for Exp(B)
Lower Upper
Sex .328 .263 1.557 1 .212 1.388 .829 2.324
BMIcat 9.129 2 .010
BMIcat(1) -.666 .420 2.517 1 .113 .514 .226 1.170
BMIcat(2) .328 .344 .909 1 .340 1.388 .707 2.725
SBP .010 .006 2.826 1 .093 1.010 .998 1.022
Chol .255 .106 5.767 1 .016 1.290 1.048 1.588
Ageinyears .042 .014 9.315 1 .002 1.042 1.015 1.071

Interpretation
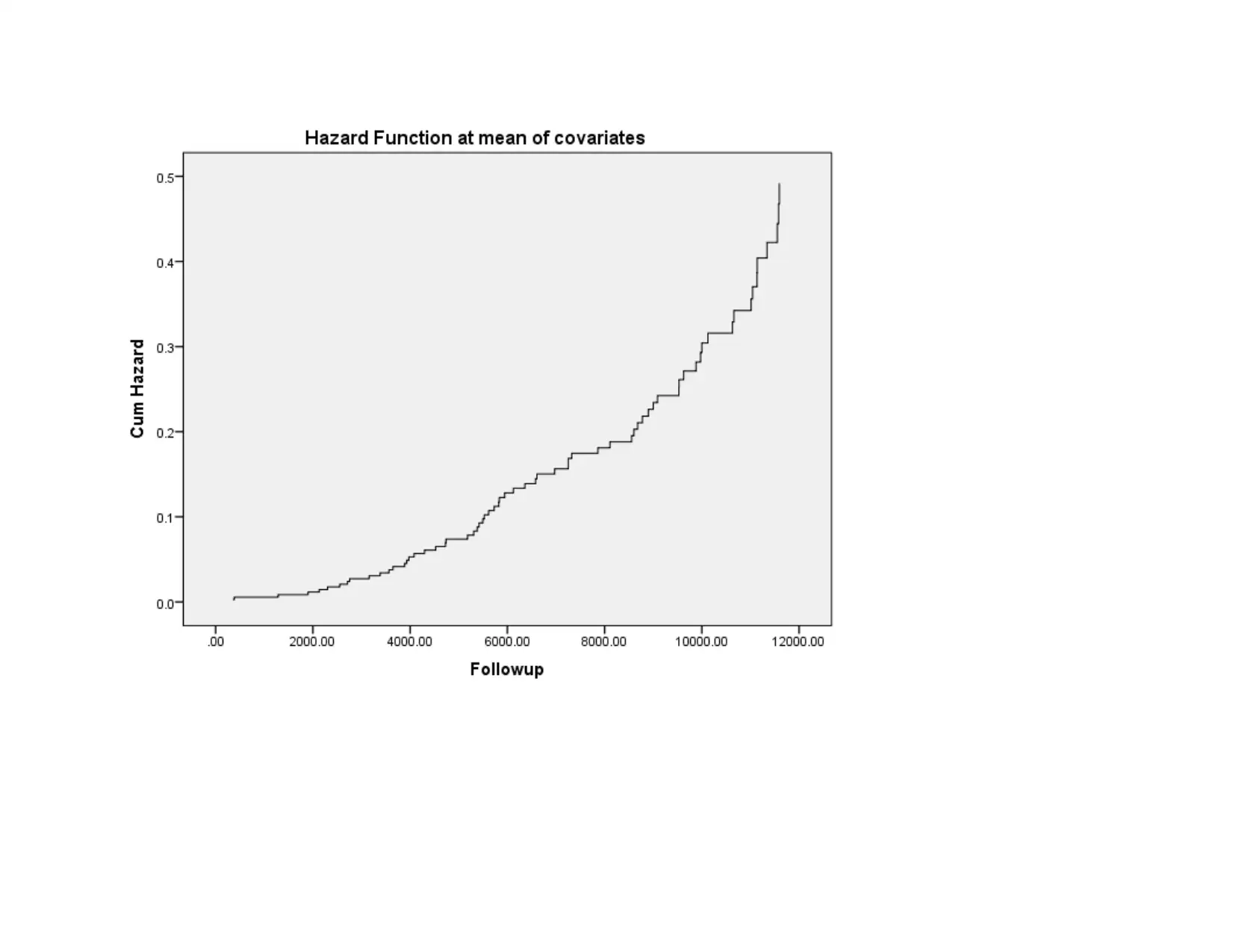
In the above given model an attempt is made to identify the determine whether time to develop coronary heart disease depends
on the explanatory variables gender, BMI category, systolic blood pressure, cholesterol and age. The output of the Cox regression
state that age is the statistically significant predictor of time to develop coronary heart disease. On analysis of results it is identified
that variable time to develop coronary heart disease depends on age in years as there is significant difference between both as reflected
by P value. In case of other variables p value is less than 0.05 which means that in case of other variables there is no significant
difference between dependent and independent variables. The hazard ratio is 1.048 which indicate that risk of dying increases 1048
times with each year increase in age. Thus, it can be said that it is the age factor that heavily play an important role in origination of
coronary heart disease in human body. Results are clearly indicating that with change in covariates which are BMI, SBP and chol
hazard probability increased at rapid pace which means that with increase in values of these covariates probability of suffering from
CHD increased at rapid pace.
(d) Significance of Cox proportional hazards model rather that logistic regression to determine which factors are associated with
coronary heart disease
Work that is done by the logistic regression is also done by the Cox proportional hazards model. The only difference between
both models is that Cox model is very flexible in nature. On this basis it probability of happening of certain event in any situation is
easily identified in the Cox model then logistic regression model. Thus, it can be said that there is Significance of Cox proportional
hazards model rather that logistic regression to determine which factors are associated with coronary heart disease.
CONCLUSION
On the basis of above discussion it is concluded that heart disease have severe impact on health of an individuals and it is the
age factor that heavily affect the probability of occurrence of health disease in the human body. Blood pressure level is affected by the
In the above given model an attempt is made to identify the determine whether time to develop coronary heart disease depends
on the explanatory variables gender, BMI category, systolic blood pressure, cholesterol and age. The output of the Cox regression
state that age is the statistically significant predictor of time to develop coronary heart disease. On analysis of results it is identified
that variable time to develop coronary heart disease depends on age in years as there is significant difference between both as reflected
by P value. In case of other variables p value is less than 0.05 which means that in case of other variables there is no significant
difference between dependent and independent variables. The hazard ratio is 1.048 which indicate that risk of dying increases 1048
times with each year increase in age. Thus, it can be said that it is the age factor that heavily play an important role in origination of
coronary heart disease in human body. Results are clearly indicating that with change in covariates which are BMI, SBP and chol
hazard probability increased at rapid pace which means that with increase in values of these covariates probability of suffering from
CHD increased at rapid pace.
(d) Significance of Cox proportional hazards model rather that logistic regression to determine which factors are associated with
coronary heart disease
Work that is done by the logistic regression is also done by the Cox proportional hazards model. The only difference between
both models is that Cox model is very flexible in nature. On this basis it probability of happening of certain event in any situation is
easily identified in the Cox model then logistic regression model. Thus, it can be said that there is Significance of Cox proportional
hazards model rather that logistic regression to determine which factors are associated with coronary heart disease.
CONCLUSION
On the basis of above discussion it is concluded that heart disease have severe impact on health of an individuals and it is the
age factor that heavily affect the probability of occurrence of health disease in the human body. Blood pressure level is affected by the
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

cholesterol level in the human body. If cholesterol level will increase in the human body blood pressure may increase significantly. It
is also concluded that blood pressure level in the human body is not much depending upon the gender factor. This means that if blood
pressure level will increased then in that case gender does not play any role in same.
is also concluded that blood pressure level in the human body is not much depending upon the gender factor. This means that if blood
pressure level will increased then in that case gender does not play any role in same.
1 out of 32
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





