Which Stock Should I Invest In PHUONG THAO BUI
VerifiedAdded on 2023/05/05
|11
|2540
|64
AI Summary
In this report we will discuss about Investing and below are the summaries point:-
Monthly historical data was given for S&P 500 Price Index, Boeing Company Stock Price, General Dynamics Corp. Stock Price, and interest rate on 10 years of the US-Treasury Note from Jan 1st 2013 to Jan 1st 2018 (Group 1).
The average return and standard deviation of Boeing (BA) stocks were 2.6134 and 6.5066 respectively, while GD stocks had an average return of 2.0177 with a standard deviation of 4.1805.
Boeing Company had a higher average return than that of General Dynamics Corporate, but BA stock was riskier than GD stocks based on the standard deviation.
The null hypothesis (H0) was that the distribution of both stocks was normal, and the alternative hypothesis (H1) was that the distribution was unnormal with a level of significance of 5%.
The Jarque-Berra (JB) test was used to evaluate the normality of the distribution, and the test statistic was computed using the formulas for JB.
For BA return stock, the null hypothesis was not rejected as p-value > 5% and the JB value < CV-Chisquare.
For GD return stock, the null hypothesis was rejected as p-value < 5% and the JB value > CV-Chisquare.
The F-test was used to test the null hypothesis that the variances of the two stocks were equal.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

WHICH STOCK
SHOULD I INVEST
IN
PHUONG THAO BUI
18809943
SHOULD I INVEST
IN
PHUONG THAO BUI
18809943
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
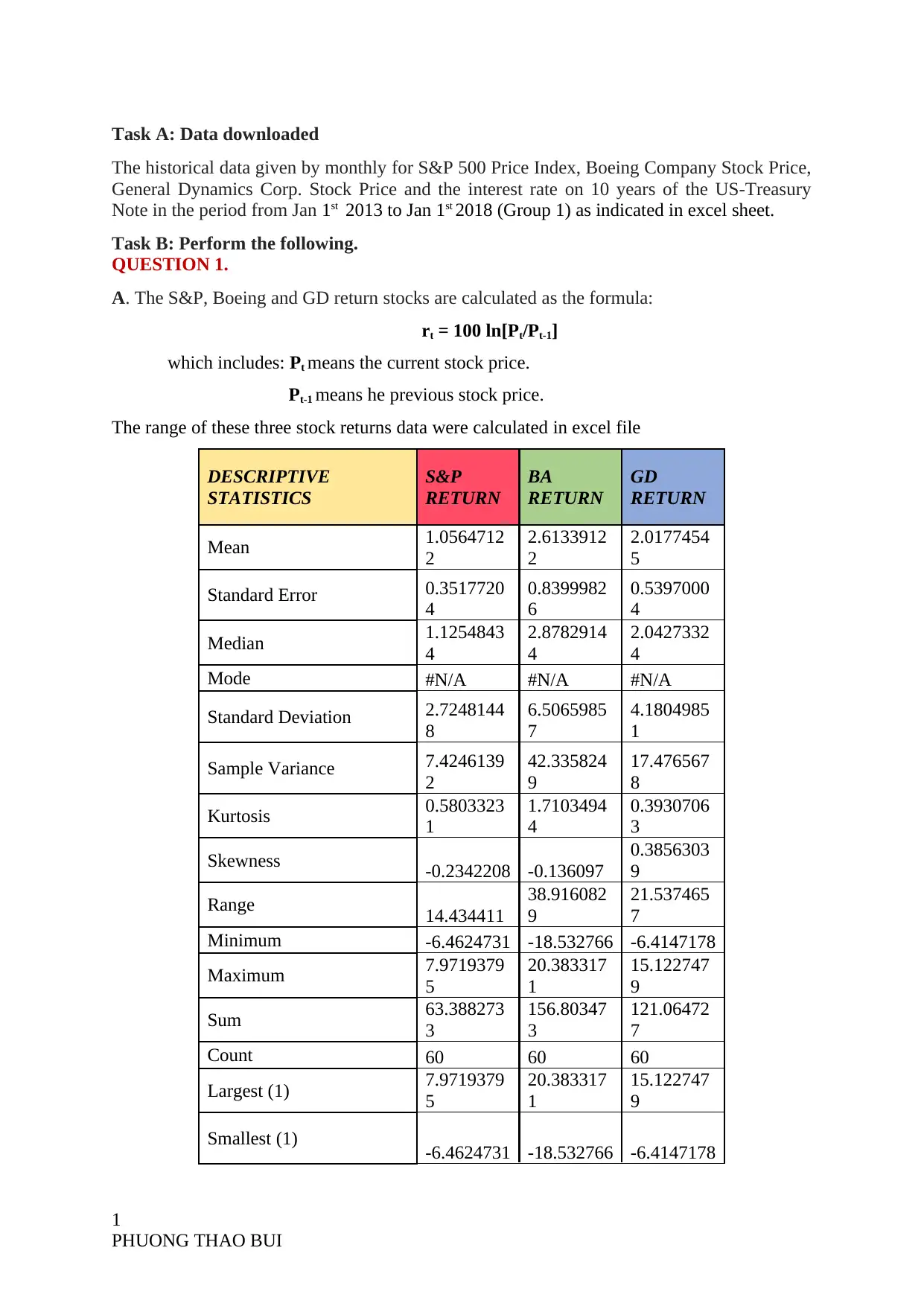
Task A: Data downloaded
The historical data given by monthly for S&P 500 Price Index, Boeing Company Stock Price,
General Dynamics Corp. Stock Price and the interest rate on 10 years of the US-Treasury
Note in the period from Jan 1st 2013 to Jan 1st 2018 (Group 1) as indicated in excel sheet.
Task B: Perform the following.
QUESTION 1.
A. The S&P, Boeing and GD return stocks are calculated as the formula:
rt = 100 ln[Pt/Pt-1]
which includes: Pt means the current stock price.
Pt-1 means he previous stock price.
The range of these three stock returns data were calculated in excel file
DESCRIPTIVE
STATISTICS
S&P
RETURN
BA
RETURN
GD
RETURN
Mean 1.0564712
2
2.6133912
2
2.0177454
5
Standard Error 0.3517720
4
0.8399982
6
0.5397000
4
Median 1.1254843
4
2.8782914
4
2.0427332
4
Mode #N/A #N/A #N/A
Standard Deviation 2.7248144
8
6.5065985
7
4.1804985
1
Sample Variance 7.4246139
2
42.335824
9
17.476567
8
Kurtosis 0.5803323
1
1.7103494
4
0.3930706
3
Skewness -0.2342208 -0.136097
0.3856303
9
Range 14.434411
38.916082
9
21.537465
7
Minimum -6.4624731 -18.532766 -6.4147178
Maximum 7.9719379
5
20.383317
1
15.122747
9
Sum 63.388273
3
156.80347
3
121.06472
7
Count 60 60 60
Largest (1) 7.9719379
5
20.383317
1
15.122747
9
Smallest (1) -6.4624731 -18.532766 -6.4147178
1
PHUONG THAO BUI
The historical data given by monthly for S&P 500 Price Index, Boeing Company Stock Price,
General Dynamics Corp. Stock Price and the interest rate on 10 years of the US-Treasury
Note in the period from Jan 1st 2013 to Jan 1st 2018 (Group 1) as indicated in excel sheet.
Task B: Perform the following.
QUESTION 1.
A. The S&P, Boeing and GD return stocks are calculated as the formula:
rt = 100 ln[Pt/Pt-1]
which includes: Pt means the current stock price.
Pt-1 means he previous stock price.
The range of these three stock returns data were calculated in excel file
DESCRIPTIVE
STATISTICS
S&P
RETURN
BA
RETURN
GD
RETURN
Mean 1.0564712
2
2.6133912
2
2.0177454
5
Standard Error 0.3517720
4
0.8399982
6
0.5397000
4
Median 1.1254843
4
2.8782914
4
2.0427332
4
Mode #N/A #N/A #N/A
Standard Deviation 2.7248144
8
6.5065985
7
4.1804985
1
Sample Variance 7.4246139
2
42.335824
9
17.476567
8
Kurtosis 0.5803323
1
1.7103494
4
0.3930706
3
Skewness -0.2342208 -0.136097
0.3856303
9
Range 14.434411
38.916082
9
21.537465
7
Minimum -6.4624731 -18.532766 -6.4147178
Maximum 7.9719379
5
20.383317
1
15.122747
9
Sum 63.388273
3
156.80347
3
121.06472
7
Count 60 60 60
Largest (1) 7.9719379
5
20.383317
1
15.122747
9
Smallest (1) -6.4624731 -18.532766 -6.4147178
1
PHUONG THAO BUI

Confidence Level (95.0%) 0.7038942
2
1.6808326
4
1.0799372
8
It can be clearly seen from the table that the average return and standard deviation of Boeing
(BA) stocks is 2.6134 and 6.5066 respectively whilst GD stocks had the average return of
2.0177 with a standard deviation of 4.1805. Hence, Boeing Company had the average return
higher than that of General Dynamics Corporate. Simultaneously, the standard deviation is
suggestive the instability of the returns and the risk, in this case, BA stock had a fairly riskier
than GD stocks. In conclusion, the stock of Boeing had a higher average of returns as well as
a relative higher risk than GD stock.
B. Jarque–Bera test
Step 1: Hypothesis
H0: The distributions is normal
H1: The distribution is unnormal
Step 2: Level of significance
Assuming the level of significance =5%
Step 3: Test Statistic
Using Jarque-Berra (JB) test to evaluate the normality of the distribution. To be more
specific, the JB test statistic predicts the distribution of Chi-square through the null
hypothesis (Ho) with two freedom degrees (the skewness S and the excess kurtosis (K-3)).
The formulas of JB is computed by:
In addition, the Chi-square test is calculated by the formula in excel
=CHISQ.INV.RT(significance level, degrees of freedom)
After computing the formulas in excel, the results were indicated in the table below:
BA GD Excel Formulas
n 60 60
Skewness (S) -0.1361 0.3856
Excess Kurtosis
(K-3) 1.7103 0.3931
JB 4.3432 18.4773
CV-Chi-square 5.9915 5.9915 =CHISQ.INV.RT(significance level, degrees of
2
PHUONG THAO BUI
2
1.6808326
4
1.0799372
8
It can be clearly seen from the table that the average return and standard deviation of Boeing
(BA) stocks is 2.6134 and 6.5066 respectively whilst GD stocks had the average return of
2.0177 with a standard deviation of 4.1805. Hence, Boeing Company had the average return
higher than that of General Dynamics Corporate. Simultaneously, the standard deviation is
suggestive the instability of the returns and the risk, in this case, BA stock had a fairly riskier
than GD stocks. In conclusion, the stock of Boeing had a higher average of returns as well as
a relative higher risk than GD stock.
B. Jarque–Bera test
Step 1: Hypothesis
H0: The distributions is normal
H1: The distribution is unnormal
Step 2: Level of significance
Assuming the level of significance =5%
Step 3: Test Statistic
Using Jarque-Berra (JB) test to evaluate the normality of the distribution. To be more
specific, the JB test statistic predicts the distribution of Chi-square through the null
hypothesis (Ho) with two freedom degrees (the skewness S and the excess kurtosis (K-3)).
The formulas of JB is computed by:
In addition, the Chi-square test is calculated by the formula in excel
=CHISQ.INV.RT(significance level, degrees of freedom)
After computing the formulas in excel, the results were indicated in the table below:
BA GD Excel Formulas
n 60 60
Skewness (S) -0.1361 0.3856
Excess Kurtosis
(K-3) 1.7103 0.3931
JB 4.3432 18.4773
CV-Chi-square 5.9915 5.9915 =CHISQ.INV.RT(significance level, degrees of
2
PHUONG THAO BUI

freedom)
p-value 0.1140
0.00009
7
=CHISQ.DIST. RT (Test statistic's value, degrees
of freedom)
Step 4: Decision Rule
Reject H0 if p-value is less than 5% (p-value < 5%) or if JB> 2=5.99
Step 5: Decision and interpretation
In term of BA return stock, since the p-value of BA > 5% (0.114 > 0.05) and the JB value
<CV- Chisquare (4.3432 < 5.9915). Therefore, the null hypothesis (H0) for the test is failed
to reject which means the data of the return of Boeing stock is normally distributed.
In contrast, in terms of GD return stock, the p-value < 5% (0.000097 < 0.05) and the JB value
> CV-Chisquare (18.4773 > 5.9915). Thus, the data of returns of GD are not normally
distributed since then the null hypothesis (H0) is rejected.
QUESTION 2
The testing of hypothesis has been applied to evaluate whether the average return on GD
stock is at least 2.8% or not.
Step 1: Hypothesis
H0: 2.8 (the average return on Boeing stock is at least 2.8%)
H1: < 2.8
As a result, the hypothesis is considered as one-sided and left-tailed test.
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic and observed value
Since the observation is large (n>30) and also the distribution is normal with unknown
population standard deviation σ, then the rational test statistic is . According to
Central Limit Theorem, the observation has estimated to normal distribution. Since then,
the formulas for the standard normal distribution is applied as below:
Description statistic of the return on Boeing stock is computed from the function of excel
as figured out below:
3
PHUONG THAO BUI
p-value 0.1140
0.00009
7
=CHISQ.DIST. RT (Test statistic's value, degrees
of freedom)
Step 4: Decision Rule
Reject H0 if p-value is less than 5% (p-value < 5%) or if JB> 2=5.99
Step 5: Decision and interpretation
In term of BA return stock, since the p-value of BA > 5% (0.114 > 0.05) and the JB value
<CV- Chisquare (4.3432 < 5.9915). Therefore, the null hypothesis (H0) for the test is failed
to reject which means the data of the return of Boeing stock is normally distributed.
In contrast, in terms of GD return stock, the p-value < 5% (0.000097 < 0.05) and the JB value
> CV-Chisquare (18.4773 > 5.9915). Thus, the data of returns of GD are not normally
distributed since then the null hypothesis (H0) is rejected.
QUESTION 2
The testing of hypothesis has been applied to evaluate whether the average return on GD
stock is at least 2.8% or not.
Step 1: Hypothesis
H0: 2.8 (the average return on Boeing stock is at least 2.8%)
H1: < 2.8
As a result, the hypothesis is considered as one-sided and left-tailed test.
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic and observed value
Since the observation is large (n>30) and also the distribution is normal with unknown
population standard deviation σ, then the rational test statistic is . According to
Central Limit Theorem, the observation has estimated to normal distribution. Since then,
the formulas for the standard normal distribution is applied as below:
Description statistic of the return on Boeing stock is computed from the function of excel
as figured out below:
3
PHUONG THAO BUI
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

GD RETURN
Mean 2.0177
Standard Error 0.5397
Median 2.0427
Mode #N/A
Standard Deviation 4.1805
Sample Variance 17.4766
Kurtosis 0.3931
Skewness 0.3856
Range 21.5375
Minimum -6.4147
Maximum 15.1227
Sum 121.0647
Count 60
Largest(1) 15.1227
Smallest(1) -6.4147
Confidence Level(95.0%) 1.0799
After that, the formulas is used: t-obs= (2.0177 -2.8)/(4.1805/√ 60) =-1.4494
Step 4: Decision rule
Reject H0 if t-obs < -1.645 or p-value < 5%,
Step 5: Decision and interpretation
Since t-obs > tα,n-1 (-1.4494> -1.645), thus, there is insufficient statistical evidence to
reject the state that the average of GD's return stock is at least 2.8%. Thus, it could be
summarized that the average return on GD stock is less than 2.8%.
QUESTION 3
The test of hypothesis has been carried out to verify if the risk of both stocks hasthe same
or not. The proper test is F-test which is applied to evaluate the null hypothesis (H0_ of
the variances of two stocks are equal.
Step 1: Hypothesis
H0: σBA2= σGD2
H1: σBA2 ≠ σGD2
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic
F = sBA2/ sGD2
4
PHUONG THAO BUI
Mean 2.0177
Standard Error 0.5397
Median 2.0427
Mode #N/A
Standard Deviation 4.1805
Sample Variance 17.4766
Kurtosis 0.3931
Skewness 0.3856
Range 21.5375
Minimum -6.4147
Maximum 15.1227
Sum 121.0647
Count 60
Largest(1) 15.1227
Smallest(1) -6.4147
Confidence Level(95.0%) 1.0799
After that, the formulas is used: t-obs= (2.0177 -2.8)/(4.1805/√ 60) =-1.4494
Step 4: Decision rule
Reject H0 if t-obs < -1.645 or p-value < 5%,
Step 5: Decision and interpretation
Since t-obs > tα,n-1 (-1.4494> -1.645), thus, there is insufficient statistical evidence to
reject the state that the average of GD's return stock is at least 2.8%. Thus, it could be
summarized that the average return on GD stock is less than 2.8%.
QUESTION 3
The test of hypothesis has been carried out to verify if the risk of both stocks hasthe same
or not. The proper test is F-test which is applied to evaluate the null hypothesis (H0_ of
the variances of two stocks are equal.
Step 1: Hypothesis
H0: σBA2= σGD2
H1: σBA2 ≠ σGD2
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic
F = sBA2/ sGD2
4
PHUONG THAO BUI

F-Test Two-Sample for Variances
BA RETURN
GD
RETURN
Mean 2.6134 2.0177
Variance 42.3358 17.4766
Observations 60 60
df 59 59
F 2.4224
P(F<=f) one-tail 0.00043
F Critical one-tail 1.5400
Calculating the critical values F:
F = sBA2/ sGD2 = 42.3358/17.4766 = 2.4224
Right-tailed CV = F.INV.RT(0.025,60,60) =1.6741
Left-tailed CV = 1/Right-tailed CV=1/1.6668 = 0.5973
p-value = 2* p-value one-tail = 2* 0.00043 = 0.00087
Step 4: Decision rule
Reject H0 if p-value < 5%,
Step 5: Decision and interpretation
Since p-value < 5% (0.00087< 0.05), hence, the null hypothesis is rejected and thus
conclude that there is sufficient statistical evidence that the variances of two stocks are
equal => The risk of two stocks (BA and GD) are equal.
QUESTION 4
To examine whether two stocks (BA and GD) have the same the average of return
population or not, we applied hypothesis testing. The sample involve in the independent
of variables with the sample size is higher than 30 and unknown population variances.
Thus, the distribution could be roughly normal based on Central Limit Theorem.
Step 1: Hypothesis
H0: μBA= μGD (The same population average return of two stocks)
H1: μBA≠ μGD
Step 2: Level of significane
Using level of significance =5%.
5
PHUONG THAO BUI
BA RETURN
GD
RETURN
Mean 2.6134 2.0177
Variance 42.3358 17.4766
Observations 60 60
df 59 59
F 2.4224
P(F<=f) one-tail 0.00043
F Critical one-tail 1.5400
Calculating the critical values F:
F = sBA2/ sGD2 = 42.3358/17.4766 = 2.4224
Right-tailed CV = F.INV.RT(0.025,60,60) =1.6741
Left-tailed CV = 1/Right-tailed CV=1/1.6668 = 0.5973
p-value = 2* p-value one-tail = 2* 0.00043 = 0.00087
Step 4: Decision rule
Reject H0 if p-value < 5%,
Step 5: Decision and interpretation
Since p-value < 5% (0.00087< 0.05), hence, the null hypothesis is rejected and thus
conclude that there is sufficient statistical evidence that the variances of two stocks are
equal => The risk of two stocks (BA and GD) are equal.
QUESTION 4
To examine whether two stocks (BA and GD) have the same the average of return
population or not, we applied hypothesis testing. The sample involve in the independent
of variables with the sample size is higher than 30 and unknown population variances.
Thus, the distribution could be roughly normal based on Central Limit Theorem.
Step 1: Hypothesis
H0: μBA= μGD (The same population average return of two stocks)
H1: μBA≠ μGD
Step 2: Level of significane
Using level of significance =5%.
5
PHUONG THAO BUI

Step 3: Test Statistic
BA and GD stocks are not dependent with unknown population variances, and the
sample size of (n1, n2) > 30 as well. Based on JB test calculated in the previous part, two
stocks have normal distribution and F-test and equal variances. Hence, the precise test
statistic is t-test with two-sample assuming equal variances.
t-Test: Two-Sample Assuming Equal Variances
BA
RETURN
GD
RETURN
Mean 2.6134 2.0177
Variance 42.3358 17.4766
Observations 60 60
Pooled Variance 29.9062
Hypothesized Mean Difference 0
df 118
t Stat 0.5966
P(T<=t) one-tail 0.2760
t Critical one-tail 1.6579
P(T<=t) two-tail 0.5519
t Critical two-tail 1.9803
Step 4: Decision rule
Reject H0 if t-obs< -1.96 or t-obs> 1.96 (n>30, since then using z - critical values)
Or if p - value < 0.05
Step 5:Conclusion
Since t-obs is not belonged in the rejection region (-1.96<0.5966<1.96), thus, the null
hypothesis (H0) cannot be rejected due to the insufficient statistical evidence. Therefore,
the Boeing's stock and GD's stock have the same population average return.
Based on the earlier hypothesis testing, two stocks have the same population average
return and equal risk. Conversely, according to the statistical summary of two stocks in
question 1, it showed that Boeing had a greater average return (mean) and fairly riskier
6
PHUONG THAO BUI
BA and GD stocks are not dependent with unknown population variances, and the
sample size of (n1, n2) > 30 as well. Based on JB test calculated in the previous part, two
stocks have normal distribution and F-test and equal variances. Hence, the precise test
statistic is t-test with two-sample assuming equal variances.
t-Test: Two-Sample Assuming Equal Variances
BA
RETURN
GD
RETURN
Mean 2.6134 2.0177
Variance 42.3358 17.4766
Observations 60 60
Pooled Variance 29.9062
Hypothesized Mean Difference 0
df 118
t Stat 0.5966
P(T<=t) one-tail 0.2760
t Critical one-tail 1.6579
P(T<=t) two-tail 0.5519
t Critical two-tail 1.9803
Step 4: Decision rule
Reject H0 if t-obs< -1.96 or t-obs> 1.96 (n>30, since then using z - critical values)
Or if p - value < 0.05
Step 5:Conclusion
Since t-obs is not belonged in the rejection region (-1.96<0.5966<1.96), thus, the null
hypothesis (H0) cannot be rejected due to the insufficient statistical evidence. Therefore,
the Boeing's stock and GD's stock have the same population average return.
Based on the earlier hypothesis testing, two stocks have the same population average
return and equal risk. Conversely, according to the statistical summary of two stocks in
question 1, it showed that Boeing had a greater average return (mean) and fairly riskier
6
PHUONG THAO BUI
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
(standard deviation) than GD whilst the kurtosis is insignificant different. Thus, my
preferred stock is Boeing (BA).
QUESTION 5
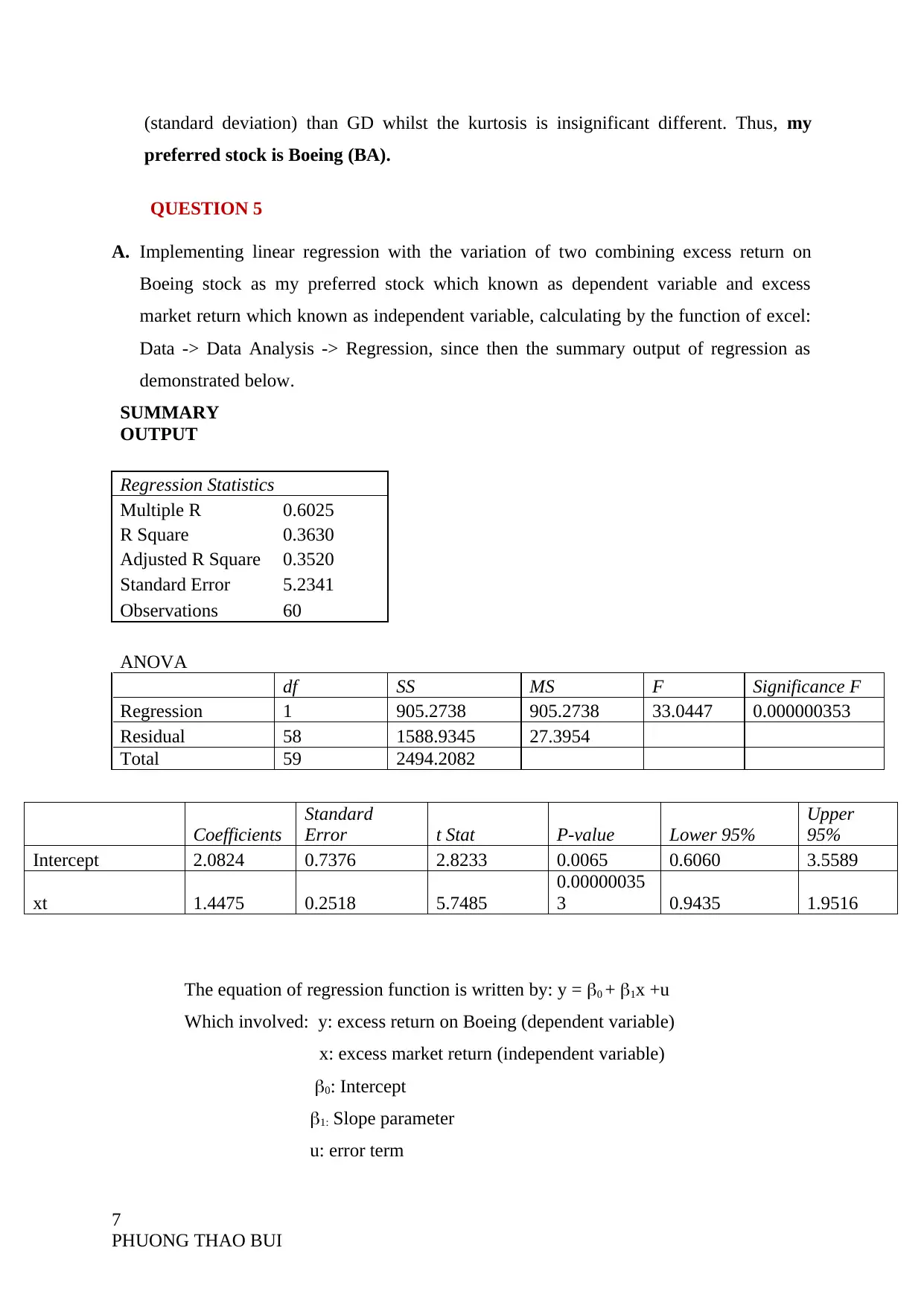
A. Implementing linear regression with the variation of two combining excess return on
Boeing stock as my preferred stock which known as dependent variable and excess
market return which known as independent variable, calculating by the function of excel:
Data -> Data Analysis -> Regression, since then the summary output of regression as
demonstrated below.
SUMMARY
OUTPUT
Regression Statistics
Multiple R 0.6025
R Square 0.3630
Adjusted R Square 0.3520
Standard Error 5.2341
Observations 60
ANOVA
df SS MS F Significance F
Regression 1 905.2738 905.2738 33.0447 0.000000353
Residual 58 1588.9345 27.3954
Total 59 2494.2082
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Intercept 2.0824 0.7376 2.8233 0.0065 0.6060 3.5589
xt 1.4475 0.2518 5.7485
0.00000035
3 0.9435 1.9516
The equation of regression function is written by: y = 0 + 1x +u
Which involved: y: excess return on Boeing (dependent variable)
x: excess market return (independent variable)
0: Intercept
1: Slope parameter
u: error term
7
PHUONG THAO BUI
preferred stock is Boeing (BA).
QUESTION 5
A. Implementing linear regression with the variation of two combining excess return on
Boeing stock as my preferred stock which known as dependent variable and excess
market return which known as independent variable, calculating by the function of excel:
Data -> Data Analysis -> Regression, since then the summary output of regression as
demonstrated below.
SUMMARY
OUTPUT
Regression Statistics
Multiple R 0.6025
R Square 0.3630
Adjusted R Square 0.3520
Standard Error 5.2341
Observations 60
ANOVA
df SS MS F Significance F
Regression 1 905.2738 905.2738 33.0447 0.000000353
Residual 58 1588.9345 27.3954
Total 59 2494.2082
Coefficients
Standard
Error t Stat P-value Lower 95%
Upper
95%
Intercept 2.0824 0.7376 2.8233 0.0065 0.6060 3.5589
xt 1.4475 0.2518 5.7485
0.00000035
3 0.9435 1.9516
The equation of regression function is written by: y = 0 + 1x +u
Which involved: y: excess return on Boeing (dependent variable)
x: excess market return (independent variable)
0: Intercept
1: Slope parameter
u: error term
7
PHUONG THAO BUI

The p-value of the excess market return is 0.000000353 that is significant smaller than 0.05.
Thus, the excess return on Boeing is exactly predicted by the excess market return.
Hence, the fitted line is:
yt^= 2.0824+ 1.4475 * xt
B. Interpret the estimated CAPM beta-coefficient.
The beta-coefficient estimation (the intercept for regression) is 2.0824. According to this
regression testing, it embodied for a predicted of the excess return on Boeing of 2.0824%
once the excess market return is zero. In conclusion, Boeing stock is considered as a cost-
effective and profitable returns for the stockholders.
C. Interpret the value of R2.
The R2 value is 0.3630 which means that 36.30% variation in the excess return on Boeing is
explained or predicted by the excess market return, and the remaining 63.70% variation is
unexplained.
D. Interpret 95% confidence interval for the slope coefficient.
The slope coefficient (1) of 1.4475 which means that an additional 1% in the excess market
return will increase the excess return of Boeing by 1.4475% on average.
QUESTION 6
By applying the confidence interval to approach the hypothesis testing, we can evaluate
whether my preferred Boeing stock is considered as a neutral stock or not. It means that the
stock has 1 of 1.
Step 1: Hypothesis
H0: 1 = 1 (The stock of Boeing is neutral)
H1: 1 1 (The stock of Boeing is not neutral)
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic
It can be clearly seen from the problem previously, at the significance level of 5%, the 1
for 95% CI to be (0.9435; 1.9516). The 1 can be computed by formulas:
^❑1 t(-2, -2)* SE ( ^❑1)
Coefficient
s
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 2.0824 0.7376 2.8233 0.0065 0.6060 3.5589 0.6060 3.5589
X Variable
1 1.4475 0.2518 5.7485 0.0000 0.9435 1.9516 0.9435 1.9516
8
PHUONG THAO BUI
Thus, the excess return on Boeing is exactly predicted by the excess market return.
Hence, the fitted line is:
yt^= 2.0824+ 1.4475 * xt
B. Interpret the estimated CAPM beta-coefficient.
The beta-coefficient estimation (the intercept for regression) is 2.0824. According to this
regression testing, it embodied for a predicted of the excess return on Boeing of 2.0824%
once the excess market return is zero. In conclusion, Boeing stock is considered as a cost-
effective and profitable returns for the stockholders.
C. Interpret the value of R2.
The R2 value is 0.3630 which means that 36.30% variation in the excess return on Boeing is
explained or predicted by the excess market return, and the remaining 63.70% variation is
unexplained.
D. Interpret 95% confidence interval for the slope coefficient.
The slope coefficient (1) of 1.4475 which means that an additional 1% in the excess market
return will increase the excess return of Boeing by 1.4475% on average.
QUESTION 6
By applying the confidence interval to approach the hypothesis testing, we can evaluate
whether my preferred Boeing stock is considered as a neutral stock or not. It means that the
stock has 1 of 1.
Step 1: Hypothesis
H0: 1 = 1 (The stock of Boeing is neutral)
H1: 1 1 (The stock of Boeing is not neutral)
Step 2: Level of significane
Assuming level of significance =5%.
Step 3: Test Statistic
It can be clearly seen from the problem previously, at the significance level of 5%, the 1
for 95% CI to be (0.9435; 1.9516). The 1 can be computed by formulas:
^❑1 t(-2, -2)* SE ( ^❑1)
Coefficient
s
Standard
Error t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 2.0824 0.7376 2.8233 0.0065 0.6060 3.5589 0.6060 3.5589
X Variable
1 1.4475 0.2518 5.7485 0.0000 0.9435 1.9516 0.9435 1.9516
8
PHUONG THAO BUI

As a result, the value of 1 involved in regression model with 95%CI for 1 = 0.9435;
1.9516]
Step 4: Decision rule
Reject H0 if 1 <0.9435 or 1>1.9516
Step 5: Decision
Since β1=1 which belongs to 95% confidence interval ( 0.9435 < 1< 1.9516), therefore,
the null hypothesis (Ho) cannot be rejected due to the insufficient of statistical evidence.
Hence, the Boeing stock is neutral
QUESTION 7
According to the data in the model, assuming that the error term of the distribution is
normal. To examine the error term distribution is normal, we supposed to apply JB test as
illustrated below.
The table below is summary statistics of the error term.
The Error Term
Mean 3.25665E-16
Standard Error 0.6700
Median 0.2488
Mode #N/A
Standard Deviation 5.1895
Sample Variance 26.9311
Kurtosis 1.7560
Skewness 0.6009
Range 28.7667
Minimum -12.2141
Maximum 16.5526
Sum 1.95399E-14
Count 60
Largest(1) 16.5526
Smallest(1) -12.2141
Confidence Level(95.0%) 1.3406
Step 1: Hypothesis
H0: The distribution of the error term is normal
H1: The distribution of the error term is unnormal
9
PHUONG THAO BUI
1.9516]
Step 4: Decision rule
Reject H0 if 1 <0.9435 or 1>1.9516
Step 5: Decision
Since β1=1 which belongs to 95% confidence interval ( 0.9435 < 1< 1.9516), therefore,
the null hypothesis (Ho) cannot be rejected due to the insufficient of statistical evidence.
Hence, the Boeing stock is neutral
QUESTION 7
According to the data in the model, assuming that the error term of the distribution is
normal. To examine the error term distribution is normal, we supposed to apply JB test as
illustrated below.
The table below is summary statistics of the error term.
The Error Term
Mean 3.25665E-16
Standard Error 0.6700
Median 0.2488
Mode #N/A
Standard Deviation 5.1895
Sample Variance 26.9311
Kurtosis 1.7560
Skewness 0.6009
Range 28.7667
Minimum -12.2141
Maximum 16.5526
Sum 1.95399E-14
Count 60
Largest(1) 16.5526
Smallest(1) -12.2141
Confidence Level(95.0%) 1.3406
Step 1: Hypothesis
H0: The distribution of the error term is normal
H1: The distribution of the error term is unnormal
9
PHUONG THAO BUI
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Step 2: Level of significance
Assuming the level of significance =5%.
Step 3: Test Statistic
The statistic test is Jarque-Berra test which involved the Chi-square distribution with 2
degrees of freedom. The formula is given below:
The critical values is obtained as illustrated below:
Error term Excel Formula
n 60
Skewness 0.6009
Excess Kurtosis 1.7560
JB 3.8691
CV-Chisquare 5.9915
=CHISQ.INV.RT(significance level, degrees of
freedom)
p-value 0.1445
=CHISQ.DIST.RT(Test statistic's value, degrees of
freedom)
Step 4: Decision Rule
Reject H0 if p-value < 5%,
or if JB> 2=5.99
Step 5: Decision and interpretation
As p-value of the test statistic of error term is less than 5% (the significance level)
(0.1445 > 0.05), hence, there is insufficient statistical evidence to reject the null
hypothesis (H0) of the normal distribution in terms of the error term. In conclusion, there
is a normally distributed errors.
10
PHUONG THAO BUI
Assuming the level of significance =5%.
Step 3: Test Statistic
The statistic test is Jarque-Berra test which involved the Chi-square distribution with 2
degrees of freedom. The formula is given below:
The critical values is obtained as illustrated below:
Error term Excel Formula
n 60
Skewness 0.6009
Excess Kurtosis 1.7560
JB 3.8691
CV-Chisquare 5.9915
=CHISQ.INV.RT(significance level, degrees of
freedom)
p-value 0.1445
=CHISQ.DIST.RT(Test statistic's value, degrees of
freedom)
Step 4: Decision Rule
Reject H0 if p-value < 5%,
or if JB> 2=5.99
Step 5: Decision and interpretation
As p-value of the test statistic of error term is less than 5% (the significance level)
(0.1445 > 0.05), hence, there is insufficient statistical evidence to reject the null
hypothesis (H0) of the normal distribution in terms of the error term. In conclusion, there
is a normally distributed errors.
10
PHUONG THAO BUI
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





